城市複雜性的數學難題 - 彭博社

電子藝術在直觀層面上，我們知道一個只有一個交通信號燈的小村莊遠比倫敦或紐約市簡單得多。但是否有可能準確測量任何給定城市的相對複雜性？你需要包括哪些變量？

開始並不難。我們可以先考察一個城市的人口、經濟產出和物理面積（這些都已被路易斯·貝滕科特、傑弗裏·韋斯特及其在聖菲研究所的同事們探討過）。但接下來該怎麼做？對城市基礎設施及其如何協同工作的核算？對城市邊界內發生的社會行為的分析？自然生態系統與人類干預的反饋循環？你又該如何劃定界限？是否有一個單一的數字可以在某種程度上涵蓋城市的複雜本質？

彭博社城市實驗室等待教堂轉為住房開發的奇蹟埃裏克·亞當斯對修復紐約市“不公平”財產税的消失承諾《黑色神話：悟空》為偏遠中國省份帶來了遊客狂潮解鎖區域規劃的隱藏力量，無論好壞在物理學的世界裏，有一個接近這個概念的數字，稱為科爾莫戈洛夫複雜性。這是測量複雜性的眾多方法之一，它試圖測量能夠描述所考察模式或對象的算法的大小。

例如，讓我們看一下以下兩個數字序列：

121212121212121212……

31415926535897932……

雖然這兩個序列都是規律的，但第一個只需要簡單地重複“12”的算法，而第二個則是一個更復雜的序列，需要我們開發一個生成π數字的算法。雖然算法非常精確和數學化，但我們可以將第一個序列編碼為一個簡單的句子，基本上説的是：“重複‘12’一遍又一遍。”

然而，第二個序列則需要更復雜的東西。也許像這樣：

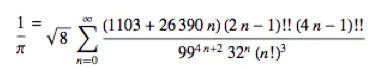第二個序列顯然需要更長和更復雜的算法描述，因此它具有更高的Kolmogorov複雜性。

要做到這一點，我們必須將城市的每個方面放入一個極其複雜的數據集中，並確定如何使用某種算法生成這些屬性。這是相當困難的。

或者我們可以使用模擬城市。

自從我年輕時，我就一直在玩模擬城市。我在1990年代初首次開始玩原版，然後升級到模擬城市2000。我記得仔細研究原版模擬城市手冊中關於城市規劃和城市性質的信息和參考資料。我記得在玩的時候等待幾個小時，以便有足夠的錢建造一個機場，或者看看可以創建的現金流為正的最小可持續城市。雖然這個遊戲絕不是實際城市的模擬（例如，城市中的科學發現似乎建模不完善），但它是我所遇到的關於城市如何真正運作的一個全面模型的最佳初步嘗試。

甚至更好的是，我們可以輕鬆地使用《模擬城市》來測量一個城市的科爾莫戈洛夫複雜性，因為我們有每個模擬城市的文件。每個文件都是一個城市的完整描述，因此其文件大小在粗略意義上是其複雜性的衡量標準。

使用一個 小數據集，包含一些在《模擬城市3000》中構建的城市的人口規模和文件大小，我檢查了複雜性如何隨人口規模變化。結果發現，城市複雜性與人口規模呈線性關係：

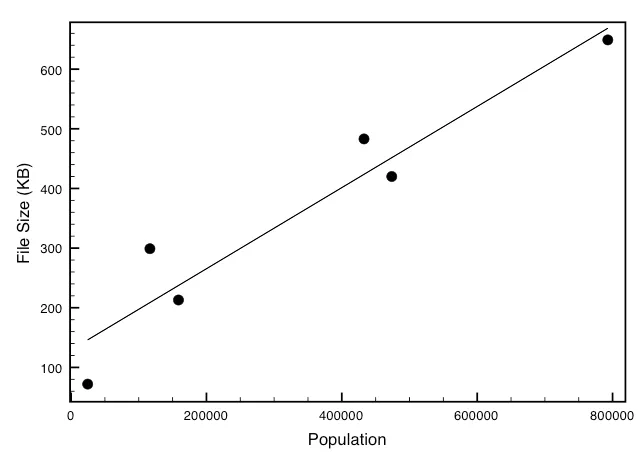這意味着，對於城市中每增加一個模擬個體，算法複雜性會增加一個恆定的量。

而能源使用的代理，例如加油站的數量，呈亞線性增長——隨着城市的發展，每人所需的加油站數量減少——而生產力和創新的代理，例如專利數量，呈超線性增長——換句話説，隨着城市的發展，每人生產的東西更多。因此，城市的整體複雜性可能是在能源使用的規模經濟和創新的遞增收益之間的平衡。

或者也可能是《模擬城市》與現實世界差異太大，我們不應該過於解讀這些結果。

還有其他嘗試更現實地建模城市，例如對 俄勒岡州波特蘭的模擬，用於更好地理解交通模式和疾病傳播。同樣，已經進行了大量工作來理解 城市的分形結構，其中城市幾何中存在某些自相似特性。

儘管如此，許多簡單模型可以用來剝離複雜系統的複雜性，幫助我們更好地理解它。也許即將推出的 更新版的模擬城市 將能夠引導我們找到更好的方法來理解如何計算壓縮整個城市。

頂部圖片：模擬城市2000的截屏* 感謝電子藝術公司

*這篇文章的早期版本錯誤地將上述截屏標識為來自模擬城市3000。它來自2000版本。