SAT幾何：潛伏的梯形，隱藏的三角形 - 彭博社

照片由 Radius Images/Corbis 提供 這個提高你 SAT 分數的建議是由 Veritas Prep 提供的。

歐幾里得幾何和座標幾何都是你在 SAT 中需要熟悉的科目，以便獲得好成績。總會有十幾個問題與幾何概念相關。雖然三角學不是 SAT 的官方主題，但你確實需要知道如何以及何時在某些問題中應用畢達哥拉斯定理。不過不用擔心：你不需要記住公式，因為每個 SAT 數學部分的開頭都會提供一個公式表。

我們想強調的是，SAT 不僅僅是將數字代入公式並得出答案；它需要你運用推理能力來判斷何時適合和有用地應用畢達哥拉斯定理。此外，有時甚至不明顯你可以應用公式來幫助你解決問題。你需要在問題中尋找“隱藏的三角形”來幫助你找到解決方案。一旦你知道要尋找什麼，你會開始在各處看到隱藏的直角三角形，並能夠利用它們來幫助你解決困難的幾何 SAT 問題。

讓我們來看一下 2007-2008 年官方 SAT 練習測試中出現的以下問題：

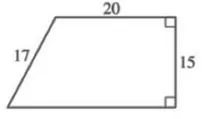
上面的梯形的周長是多少？ A) 52 B) 72 C) 75 D) 80 E) 87

你還記得在這種情況下計算梯形周長的公式嗎？你不記得？沒關係，因為沒有一個公式。那麼我們應該如何解決這個問題呢？這就是“隱藏三角形”概念發揮作用的地方。這裏的問題是我們不知道梯形底邊的長度，所以我們需要稍微創造性地解決它。仔細看看，我們可以從梯形的頂部畫一條直線到底邊，形成一個三角形，如下所示：

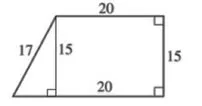
這就是我們的隱藏三角形。現在我們有一個底邊為20，邊長為15的矩形，附加在一個直角三角形上。如果我們能找出左側三角形的底邊，我們就會擁有計算整個形狀周長所需的所有組件。讓我們應用我們的勾股定理，其中17是斜邊，15是其中一條邊，我們讓x為剩餘的邊：

172 = 152 + x2 289 = 225 + x2 64 = x2 x = 8

現在我們知道三角形的底邊是20 + 8 = 28。讓我們將其他邊相加：28 + 17 + 15 + 20 = 80，或者選擇D。

你看到隱藏三角形如何幫助我們解決這個幾何問題了嗎？下次遇到SAT幾何問題時要尋找它們。

如果你對這個問題感到完全困惑，你也可以使用你的SAT考試準備策略來排除一些錯誤的答案選擇。我們知道前三條邊的總和是52（17 + 20 + 15）。我們還知道梯形的底邊必須大於頂部或大於20。因此，我們知道周長大於72。這使我們能夠排除一些太小的答案選擇：

A) 52 B) 72 C) 75 D) 80 E) 87

此外，你可能可以安全地排除答案選擇C，因為它的值太小，以及答案選擇E，因為它的值太大，基於圖形其餘部分的相對長度。無論如何，你在這個問題上獲得了優勢，即使無法達到完整的解決方案，你也會處於良好的猜測區域。一些聰明的排除策略在SAT考試中可以值幾個分數。

即將參加SAT考試？註冊試用 Veritas Prep SAT 2400按需課程。