物理學家可能永遠也無法解釋數學的強大威力_風聞

原創： Mario Livio 中科院物理所​

科學無國界

我們是知識的搬運工

作者：Mario Livio

翻譯：Nothing

審校：loulou

1960年，諾貝爾獎得主物理學家尤金.維格納寫下名為《數學在自然科學中不可思議的有效性》的文章。在這片文章中維格納寫到數學的神奇力量不僅僅包含了描述世界的能力，甚至還具有在物理世界預言現象的能力。他寫道：“數學語言在物理定律形成過程中所展現出的魔力是我們無法理解也不應得到的禮物。”

經典電磁學中所有觀測到的現象竟然都可以被四個數學公式概括！更有甚者，1864年麥克斯韋用這四個方程預言了電場或磁場可以產生向遠處傳播的波。1880年左右，赫茲用精巧的實驗首次探測到這些波。 如果這還不夠，那麼現代電動力學理論也就是量子電動力學更加令人驚詫。 2006年一個由哈佛大學物理學家組成的團隊測量到的電子磁矩值精確至萬億分之八。由量子電動力學計算得到的值也達到了相同的精度並且和實驗值吻合的很好。是什麼賦予數學如此令人難以置信的威力？在這篇短文中我不打算回答這個複雜的問題。我只是展示這個問題的一些不為人熟悉的方面。

關於數學威力的難題可能比上面提到的電動力學的例子更加複雜。 關於‘不可思議的有效性’有兩個事實，我認為其中一個是主動的，另一個是被動的。主動的一面是指當物理學家試圖照亮他們在大量實驗現象中迷宮似的道路時，他們可以將數學作為火把。換句話説，至少有些自然定律就是用數學術語構建的。在那些定律中用到的數學字符、關係和公式是按照特殊的目的發展出來的。例如牛頓，他建造了微積分這一數學的分支，因為他需要這個工具來建造他的運動方程。相似的，弦理論學家經常為了自己的需要構造數學工具。另一個是被動的方面，指的是有些情況下抽象的數學理論在創建之初就沒有考慮過應用，只有過了數十年甚至幾百年之後才會在物理模型中展現出強大的預言功能。接下來的部分，我會描述一個關於主動和被動方面相互作用的美妙的例子。

神奇的紐結

在希臘神話中，亞歷山大大帝用他的劍砍開了烏爾蒂姆烏之結，之前無數嘗試解開它的人都沒有成功（戈爾迪烏姆之結（Gordian knot）是西方傳説中的物品，神諭説，如果誰能解開這個結，那麼他就會成為亞細亞之王。）。

紐結，特別是海邊的紐結，長期被稱為“英國人的領帶”、“吊頸結”、“貓爪子”。十八世紀六十年代英國物理學家威廉.托馬斯（現在大家稱他為開爾文勳爵）真正讓紐結成為物理學的研究對象，因為他提出原子就是以太上的結。為了構造像元素週期表一樣的表，托馬斯必須要能將結分類才行，也就是説找出哪些不同的結可以存在。這個特殊需求點燃研究關於紐結的數學理論的熱情。這是我剛才提到的數學效力的積極方面。換句話説，物理學家和數學家認為紐結結是原子可行的模型，因此他們開展了對結的數學研究。

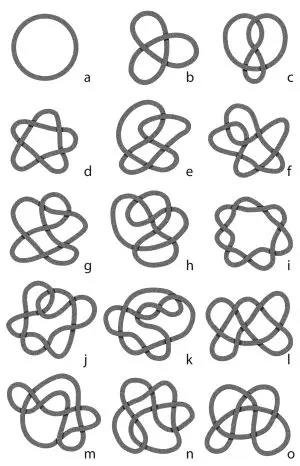
圖1. 一些紐結

一個數學上的紐結看起了和絃上的結很像，只是弦的首尾相接。在托馬斯的理論中，像圖1a1b1c中那樣的結， 至少從原則上講，可以用來表示表示越來越複雜的原子，如氫、碳、氧原子。因為紐結結真的有用，數學家尋找可以將紐結分類的精確的方法並最終找到了它-如果你無法將一個結通過簡單的操作變成另一個，那它們就是不同的。直到十九世紀末，蘇格蘭數學家Peter Guthrie Tait和Charles Newton Little發表了不少於十次交叉的結的表格。不幸的是，當這項工作發表時，托馬斯的原子結構模型已經被拋棄。然而，儘管沒有任何應用前景，紐結理論由於其自身的魅力持續吸引着數學家的興趣。唯一的不同就是，就像英國數學家Sir Michael Atiyah説的那樣：“紐結理論成純數學的一個深奧的分支。”

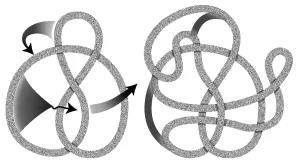
圖 2. 將一個結變形

一直以來，紐結理論的基本目標之一就是找到真正可以區分扭結的性質——也就是找到紐結不變量。紐結不變量就像是紐結的指紋一樣，它不會隨着紐結外表的變形而改變。你可能會認為一個紐結最少的交叉數可以作為這樣的不變量。畢竟，無論你怎樣嘗試，你都不能減少三葉草狀的紐結（圖1b）中的交叉數減少到3以下。然而，最小交叉數其實不是一個非常有用的不變量。像圖1顯示的那樣，有三個不同的紐結具有六個交叉，不少於七種紐結具有七個交叉。

紐結理論中的兩次重大突破分別發生在1928年和1984年。在1928年，美國數學家發現一個數學表達式，這個表達式利用交叉數組成的式子（Alexander多項式）來描述紐結。例如，三葉草扭結的Alexander多項式是t2−t+1。擁有不同多項式的紐結一定是不同的。不幸的是，兩個擁有相同多項式的紐結也可能是不同的。因此，儘管它是非常有用的，但是Alexander多項式仍然不是分類紐結的完美方法。經過幾十年的努力終於在1984年迎來了第二個突破。數學家Vaughan Jones發現了紐結理論和另一個數學分支之間的聯繫。這導致了另一種比Alexander多項式更有效的不變量的發現，新的不變量被稱為Jones多項式(瓊斯多項式)。例如，瓊斯多項式指出，即便是對於紐結和它的鏡像，多項式也是一樣的(圖3）。

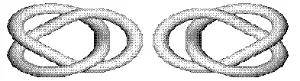
圖3. 紐結和它的鏡像

更重要的，由於瓊斯的發現，隨之而來的一系列活動突然將數學和物理領域中令人眼花繚亂的各個領域聯繫起來，甚至滲透到弦理論中——這是目前最有希望調和廣義相對論和量子力學的嘗試。

特別的，弦論學家Hirosi Ooguri和Cumrun Vafa發現很多弦之間相互作用形成的複雜拓撲結構的個數和瓊斯多項式有關。更進一步來説，弦論物理學家領袖Ed Witten發現瓊斯多項式在現代物理學最基礎的領域之一——量子場論中提供了新的見解。

從這段紐結理論的簡易歷史中可以看出。首先，它發揮了數學理論的積極作用。物理學家需要一個原子模型，然後發現紐結提供了合適的工具，因此紐結理論誕生了。當一個更好的數學模型被發現，數學家並沒有拋棄紐結理論。僅僅是被自己的好奇心驅使，他們花費數十年研究紐結的性質。在大多數數學家看來，僅僅是理解紐結的性質和找到控制其分類的原理的可能性，就已經是一種精美絕倫、不可抗拒的東西了。然而，接下來紐結理論表現出被動有效性。誰也沒想到，瓊斯多項式和紐結理論在弦論中會得到廣泛應用。

讓整個故事變得更加驚人的是這些波在1880年左右被赫茲用精巧的實驗首次探測到以下的事實：故事始於托馬斯開始研究紐結是因為他在尋找描述原子的理論，原子後來被認為是組成世界的最基礎的單元。經過歷史的輪迴，紐結現在被發現和絃論密切相關，它是我們現在理解世界的另一種方式。可以看出，紐結理論起源於解釋物理實在的努力，然後它變成了完全抽象的數學-最終又回到它最初的使命上去。這還不夠令人驚訝嗎？

原文鏈接：https://plus.maths.org/content/os/issue49/features/livio/index