這個捆綁遊戲，五百年來難住了無數高智商 | 科學DIY_風聞

【本文由公眾號“把科學帶回家”提供，ID：steamforkids】

在日本朝日放送的一檔叫做探偵!ナイトスクープ Knight Scoop 的節目裏，有一個叫做秋原俊彥的73歲老爺爺在醫生的診室裏看到了一個遊戲，然後深深入迷。他求醫生把這個遊戲送給他，然後在家花了10年時間想解開，但是做不到。不但秋原老爺子解不開，大多數觀眾也被難住了。

這個遊戲是這樣的——

這個遊戲的目標是，在不暴力拆解的情況下，讓銀環從綠球這裏到另一邊的紅球這裏。

你想到的方法大家都想過了，都不是解法。

銀環不可能套過中間那個木頭環——

銀環也不可能從木頭環的中間穿過去——

基座拆不開，繩子也繞不過去——

實際上，難住老爺爺的這個解密遊戲歷史悠久，也曾經難住了一代又一代的人。但是因為它的魅力巨大，所以一直流傳到現在，而且傳播到了許多國家，在西方和東亞都有不同的版本。

你能解開這個繩結捆綁遊戲嗎？

關鍵概念

所羅門封印

材料和操作

一根木條（也可以用粗一點的吸管代替）

一根繩子

兩個圓環

在木條上打3個洞，然後把繩子和圓環按照上面圖片裏的樣子組裝好，就可以開始玩啦。這個版本其實和一開始介紹的那個遊戲是一樣的道理，解法也是類似的。

這個遊戲的目標是，讓右邊的那個圓環和左邊的圓環貼在一起。不能把木條弄斷，也不能把繩子剪斷。

你想到解答方法了嗎？

如果你覺得有點難，那先用下面這個簡單的題目來熱熱身吧。

看看下面這個情況，應該怎樣把插頭鬆綁？

其實這個插頭是這樣解出來的——

再來一道類似的題，求如何給自己鬆綁？

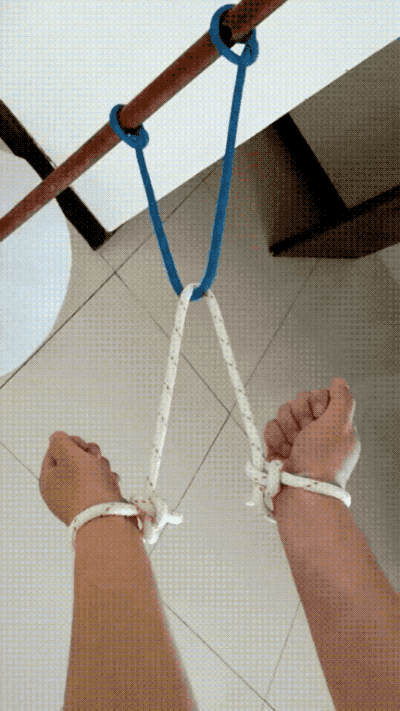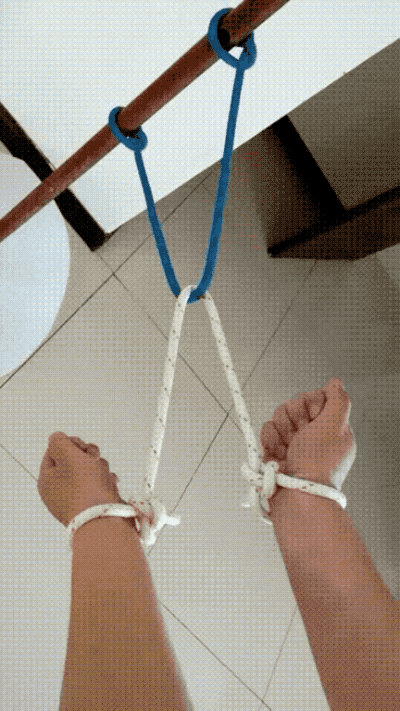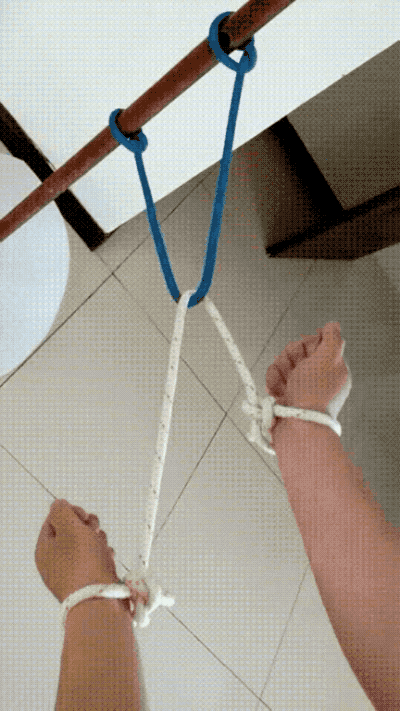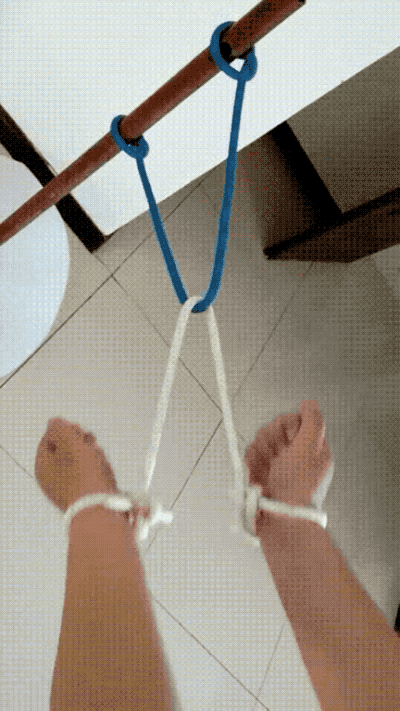
解法——

這有沒有給你一點啓示呢？

如果你還是不知道應該怎麼解，在 把科學帶回家 後台回覆 求求你告訴我，就可以得到答案啦。

原理

在這檔 Knight Scoop 節目裏，後來在日本知惠之輪協會的山本徹的幫助下，這個謎題終於得到了解答。

這個解密遊戲，在西方有 wedding rings，the ox yoke，loop de loop，african ball 或者 Solomon’s seal 等各種名字。

這個遊戲最早可以追溯到16世紀的意大利的數學家，達·芬奇（為什麼老是你？）的老友盧卡·帕西奧利（Luca Pacioli）撰寫的《De Viribus Quantitatis》（數字的力量）。

這個遊戲也有東亞的版本。這幅1836年的日本圖畫裏也描繪了這個遊戲，這也是我們上面介紹手工製作的版本。

這個遊戲的設定是這樣的，戀人 Osome 和 Hisamatsu 因為某些原因分離了，你要努力使他們重新在一起。

有很多實用主義的人會説，這些遊戲有什麼用？

其實，這些遊戲和拓撲學有關。歷史上拓撲學遊戲曾經啓發了重要的數學發現。

比如，柯尼斯堡七橋問題（Konigsberg bridge）問題就啓發了歐拉。歐拉在1736年寫了一篇論文證明這個問題無解。歐拉的這篇論文成為圖論這個數學分支的起源。

柯尼斯堡七橋問題：當時東普魯士柯尼斯堡（今日俄羅斯加里寧格勒）市區跨普列戈利亞河兩岸，河中心有兩個小島。小島與河的兩岸有七條橋連接。在所有橋都只能走一遍的前提下，如何才能把這個地方所有的橋都走遍？@wikipedia

如果上面這些遊戲都難不倒你，可以試一試下面這個進階版本的拓撲遊戲。你覺得在不暴力拆解的情況下，左圖可能變成右圖嗎？

這個拓撲遊戲其實想表達的是拓撲學裏的一個基礎概念：咖啡杯的拓撲形態和甜甜圈是一毛一樣的。

@wikipedia

好了，在拓撲學裏的解法如下。

@西山豊，大阪經濟大學

好的我知道又有人要問：“這有什麼用？”

很多人不是想知道小昭戴着鐐銬是怎麼換衣服的嗎？

這就是金庸隱藏的拓撲學答案啊！你把白色的東西看成手銬，把雙手合十的小昭看成是一個圈，你看在拓撲學的世界裏小昭的鏈子根本就沒有同時銬住她的雙手啊。

(๑• ̀д•́ )✧

大概就是因為小昭暗自掌握了這個拓撲學知識，所以金庸大俠才在《倚天屠龍記》後記裏提到小昭是他在書中最喜愛的角色吧。