見證奇蹟的時刻：從牛頓定律到波的運動 | 眾妙之門_風聞

撰文 | 長尾科技

上帝説要有光，於是就有了麥克斯韋方程組。

大家都知道麥克斯韋推導出了電磁波，然後通過計算發現電磁波的速度正好等於光速。於是，麥克斯韋就預言“光是一種電磁波”，這個預言後來被赫茲證實。

電磁波的發現讓麥克斯韋和他的電磁理論走上了神壇，也讓人類社會進入了無線電時代。你現在可以隨時給遠方的朋友打電話，能用手機刷公眾號上的文章，都跟電磁波有着密切的關係。這篇文章我們先介紹從牛頓關於粒子的運動定律，如何得出描寫波的波動方程。

01 什麼是波？

要理解電磁波，首先我們得了解什麼是波？有些人可能覺得這個問題有點奇怪，什麼是波這還用問麼？我丟一塊石頭到水裏，水面上就會形成一個水波；我抖動一根繩子，繩子上就會就會出現一個波動。生活中還有很多這種波動現象，我雖然讀書少，但是什麼是波還是知道的。

沒錯，水波、繩子上的波動這些都是波，我在這裏拋出“什麼是波？”這個問題並不是想來掰指頭數一數哪些東西是波，哪些不是，而是想問：所有這些叫作波的東西有什麼共同的特徵？我們如何用一套統一的數學語言來描述波？

我們研究物理，就是從萬千變化的自然界的各種現象裏總結出某種一致性，然後用數學的語言定量、精確的描述這種一致的現象。現在我們發現了水波、繩子上的波等許多現象都有這樣一種波動現象，那我們自然就要去尋找這種波動現象背後統一的數學規律，也就是尋找描述波動現象的方程，即波動方程。

為了尋找統一的波動方程，我們先來看看最簡單的波：抖動一根繩子，繩子上就會出現一個波沿着繩子移動，以恆定的頻率抖動就會出現連續不斷的波。

為了更好地研究繩子上的波動，我們先建立一個座標系，然後把注意力集中到其中的一個波上。於是，我們就看到一個波以一定的速度v向x軸的正方向（右邊）移動，如下圖：

那麼，我們該如何去描述這種波動呢？

首先，我們知道一個波是在不停地移動的，上圖只是波在某個時刻的樣子，它下一個時刻就會往右邊移動一點。移動了多少也很好計算：因為波速為v，所以Δt時間以後這個波就會往右移動v·Δt的距離。

另外，我不管這個時刻波是什麼形狀的曲線，反正我可以把它看成一系列的點（x,y）的集合，這樣我們就可以用一個函數y=f(x)來描述它（函數就是一種對應（映射）關係，在函數y=f(x)裏，每給定一個x，通過一定的操作f(x)就能得到一個y，這一對（x,y）就組成了座標系裏的一個點，把所有這種點連起來就得到了一條曲線）。

然後，y=f(x)只是描述某一個時刻的波的形狀，如果我們想描述一個完整動態的波，就得把時間t考慮進來。也就是説我們的波形是隨着時間變化的，即：我繩子上某個點的縱座標y不僅跟橫軸x有關，還跟時間t有關，這樣的話我們就得用一個二元函數y=f(x,t)來描述一個波。

這一步很好理解，它無非告訴我們波是隨時間（t）和空間（x）變化的。但是這樣還不夠，世界上到處都是隨着時間、空間變化的東西，比如蘋果下落、籃球在天上飛，它們跟波的本質區別又在哪呢？

02 波的本質

仔細想一下我們就會發現：波在傳播的時候，雖然不同時刻波所在的位置不一樣，但是它們的形狀始終是一樣的。也就是説前一秒波是這個形狀，一秒之後波雖然不在這個地方了，但是它依然是這個形狀，這是一個很強的限制條件。有了這個限制條件，我們就能把波和其它在時間、空間中變化的東西區分開了。

我們這樣考慮：既然用f(x,t)來描述波，那麼波的初始形狀（t=0時的形狀）就可以表示為f(x,0)。經過了時間t之後，波速為v，那麼這個波就向右邊移動了vt的距離，也就是把初始形狀f(x,0)往右移動了vt，那麼這個結果可以這樣表示：f(x-vt,0)。

為什麼把一個函數的圖像往右移動了一段vt，結果卻是用函數的自變量x減去vt，而不是加上vt呢？這是一箇中學數學問題，我這裏稍微幫大家回顧一下：你們想，如果我把一個函數圖像f(x)往右移動了3，那麼我原來在1這個地方的值f(1)，現在就成了4這個地方的函數值。所以，如果你還想用f(x)這個函數，那肯定就得用4減去3（這樣才能得到f(1)的值），而不是加3（4+3=7，f(7)在這裏可沒有什麼意義）。

所以，如果我們用f(x,t)描述波，那麼初始時刻（t=0）的波可以表示為f(x,0)。經過時間t之後的波的圖像就等於初始時刻的圖像往右移動了vt，也就是f(x-vt,0)。於是，我們就可以從數學上給出波運動的本質：

也就是説，只要有一個函數滿足f(x,t)=f(x-vt,0)，滿足任意時刻的形狀都等於初始形狀平移一段，那麼它就表示一個波。水波、聲波、繩子上的波、電磁波、引力波都是如此，這也很符合我們對波的直觀理解。

這裏我們是從純數學的角度給出了波的一個描述，下面我們再從物理的角度來分析一下波的形成原因，看看能不能得到更多的信息。

03 張  力

一根繩子放在地上的時候是靜止不動的，我們甩一下就會出現一個波動。我們想一想：這個波是怎麼傳到遠方去的呢？我們的手只是拽着繩子的一端，並沒有碰到繩子的中間，但是當這個波傳到中間的時候繩子確實動了，繩子會動就表示有力作用在它身上（牛爵爺告訴我們的道理），那麼這個力是哪裏來的呢？

稍微分析一下我們就會發現：這個力只可能來自繩子相鄰點之間的相互作用，每個點把自己隔壁的點“拉”一下，隔壁的點就動了（就跟我們列隊報數的時候只通知你旁邊的那個人一樣）這種繩子內部之間的力叫張力。

張力的概念也很好理解，比如我們用力拉一根繩子，我明明對繩子施加了一個力，但是這根繩子為什麼不會被拉長？跟我的手最近的那個點為什麼不會被拉動？

答案自然是這個點附近的點給這個質點施加了一個相反的張力，這樣這個點一邊被我拉，另一邊被它鄰近的點拉，兩個力的效果抵消了。但是力的作用又是相互的，附近的點給端點施加了一個張力，那麼這個附近的點也會受到一個來自端點的拉力，然而這個附近的點也沒動，所以它也必然會受到更裏面點的張力。這個過程可以一直傳播下去，最後的結果就是這跟繩子所有的地方都會張力。

而且，我們還可以斷定：如果繩子的質量忽略不計，繩子也沒有打結沒有被拉長，那麼繩子內部的張力處處相等（只要有一個點兩邊的張力不等，那麼這個點就應該被拉走了，繩子就會被拉變形），這是個很重要的結論。

通過上面的分析，我們知道了當一根理想繩子處於緊繃狀態的時候，繩子內部存在處處相等的張力。當一根繩子靜止在地面的時候，它處於鬆弛狀態，沒有張力，但是當一個波傳到這裏的時候，繩子會變成一個波的形狀，這時候就存在張力了。正是這種張力讓繩子上的點上下振動，所以，分析這種張力對繩子的影響就成了分析波動現象的關鍵。

04 波的受力

分析那麼，我們就從處於波動狀態的繩子中選擇很小的一段AB，我們來分析一下這個小段繩子在張力的作用下是如何運動的。放心，我們這裏並不會涉及什麼複雜的物理公式，我們所需要的公式就一個，大名鼎鼎的牛頓第二定律：F=ma。

牛頓第一定律告訴我們“一個物體在不受力或者受到的合外力為0的時候會保持靜止或者勻速直線運動狀態”，那麼如果合外力不為0呢？牛頓第二定律就接着説了：如果合外力F不為零，那麼物體就會有一個加速度a，它們之間的關係就由 F=ma 來定量描述（m是物體的質量）。也就是説，如果我們知道一個物體的質量m，只要你能分析出它受到的合外力F，那麼我們就可以根據牛頓第二定律F=ma計算出它的加速度a，知道加速度就知道它接下來要怎麼動了。

牛頓第二定律就這樣把一個物體的受力情況（F）和運動情況（a）結合起來了，我們想知道一個物體是怎麼動的，只要去去分析它受到了什麼力就行了，所以它牛。

再來看我們的波，我們從處於波動狀態的繩子裏選取很小的一段AB，我們想知道AB是怎麼運動的，就要分析它受到的合外力。因為不考慮繩子的質量，所以就不用考慮繩子的重力，那麼，我們就只要分析繩子AB兩端的張力T就行了。

如上圖，繩子AB受到A點朝左下方的張力T和B點朝右上方的張力T，而且我們還知道這兩個張力是相等的，所以才把它都記為T。但是，我們知道波動部分的繩子是彎曲的，那麼這兩個張力的方向是不一樣的，這一點從圖中可以非常明顯的看出來。我們假設A點處張力的方向跟橫軸夾角為θ，B點跟橫軸的夾角就明顯不一樣了，我們記為θ+Δθ。

因為繩子上的點在波動時是上下運動，所以我們只考慮張力T在上下方向上的分量，水平方向上的就不考慮了。那麼，我們把AB兩點的張力T都分解一下，稍微用一點三角函數的知識我們就能發現：B點處向上的張力為T·sin（θ+Δθ），A點向下的張力為T·sinθ。那麼，整個AB段在豎直方向上受到的合力就等於這兩個力相減：F= T·sin（θ+Δθ）-T·sinθ。

好了，按照牛頓第二定律F=ma，我們需要知道物體的合外力F、質量m和加速度a，現在我們已經知道了合外力F，那麼質量m和加速度a呢？

05 波的質量分析

質量好説，我們假設繩子單位長度的質量為μ，那麼長度為Δl的繩子的質量就是μ·Δl。

但是，因為我們取的是非常小的一段，我們假設A點的橫座標為x，B點的橫座標為x+Δx，也就是説繩子AB在橫座標的投影長度為Δx，那麼，當我們取的繩長非常短的時候，我們就可以近似用Δx代替Δl，這樣繩子的質量就可以表示為：μ·Δx。

質量搞定了，剩下的就是加速度a了。你可能以為我已經得到了合外力（F= T·sin（θ+Δθ）-T·sinθ）和質量m（μ·Δx），那麼剩下肯定就是用合外力F除以質量m得到加速度a（牛頓第二定律），不不不，這樣就不好玩了。我們還可以從另一個角度來得到加速度a，然後把它們作為拼盤拼起來。從哪裏得到加速度呢a？從描述波的函數f(x,t)裏。

06 波的加速度分析

不知道大家還記得我們在前面説的這個描述波的函數 y=f(x,t) 麼？這個函數的值y表示的是在x這個地方，時間為t的時候這一點的縱座標，也就是波的高度。我們現在要求的也就是AB上下波動時的加速度，那麼，怎麼從這個描述點位置的函數里求出加速度a呢？

這裏我們再來理解一下加速度a，什麼叫加速度？從名字就可以感覺到，這個量是用來衡量速度變化快慢的。加速度嘛，肯定是速度加得越快，加速度的值就越大。假如一輛車第1秒的速度是2m/s，第2秒的速度是4m/s，那麼它的加速度就是用速度的差（4-2=2）除以時間差（2-1=1），結果就是2m/s²。

再來回想一下，我們是怎麼求一輛車的速度的？我們是用距離的差來除以時間差的。比如一輛車第1秒鐘距離起點20米，第2秒鐘距離起點50米，那麼它的速度就是用距離的差（50-20=30）除以時間差（2-1=1），結果就是30m/s。

不知道大家從這兩個例子裏發現了什麼沒有？我用距離的差除以時間差就得到了速度，我再用速度的差除以時間差就得到了加速度，這兩個過程都是除以時間差。那麼，如果我把這兩個過程合到一塊呢？那是不是就可以説：距離的差除以一次時間差，再除以一次時間差就可以得到加速度？

這樣表述並不是很準確，但是可以很方便的讓大家理解這個思想。如果把距離看作關於時間的函數，我們對這個函數求一次導數（就是上面的距離差除以時間差，只不過趨於無窮小）就得到了速度的函數，對速度的函數再求一次導數就得到了加速度的表示。所以，我們把一個關於距離（位置）的函數對時間求兩次導數，就可以得到加速度的表達式。

波的函數 f(x,t) 不就是描述繩子上某一點在不同時間t的位置麼？那我們對 f(x,t) 求兩次關於時間的導數，自然就得到了這點的加速度a。因為函數f是關於x和t兩個變量的函數，所以我們只能時間的偏導∂f/ ∂t，再求一次偏導數就加個2上去。於是我們就可以這樣表示這點的加速度a=∂²f/ ∂t²。

這樣，我們就把牛頓第二定律F=ma的三要素都湊齊了：F= T·sin（θ+Δθ）-T·sinθ，m=μ·Δx，a=∂²f/ ∂t²。把它們集合在一起就可以召喚神，阿不，就可以寫出AB的運動方程了：

這個用牛頓第二定律寫出來的波動方程，看起來怎麼樣？嗯，似乎有點醜，看起來也不太清晰，方程左邊的東西看着太麻煩了，我們還需要對它進行一番改造。那怎麼改造呢？我們可以先把sinθ給幹掉。

07 方程的改造

為了能夠順利地幹掉sinθ，我們先來回顧一下基本的三角函數：

如上圖，右邊是一個直角三角形abc，那麼角θ的正弦值sinθ等於對邊c除以斜邊a，正切值tanθ等於對邊c除以鄰邊b。

當這個角度θ還很大的時候，a比b要明顯長一些。但是，一旦角度θ非常非常小，可以想象，鄰邊b和斜邊a就快要重合了。這時候我們是可以近似的認為a和b是相等的，也就是a≈b，於是就有c/b≈c/a，即tanθ≈sinθ。

也就是説，在角度θ很小的時候，我們可以用正切值tanθ代替正弦值sinθ。我們假設這跟繩子的擾動非常小，形變非常小，那麼θ和θ+Δθ就都非常小，那麼它們的正弦值就都可以用正切值代替。於是，那個波動方程左邊的sin(θ+Δθ)-sinθ就可以替換為：tan(θ+Δθ)-tanθ。

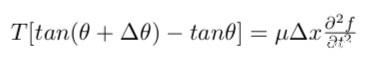
為什麼我們要用正切值tanθ代替正弦值sinθ呢？因為正切值tanθ還可以代表一條直線的斜率，代表曲線在某一點的導數。想想正切值的表達式tanθ=c/b，如果建一個座標系，那麼這個c剛好就是直線在y軸的投影dy，b就是在x軸的投影dx，它們的比值剛好就是導數dy/dx，也就是説tanθ=dy/dx。

然而，因為波的函數f(x,t)是關於x和t的二元函數，所以我們只能求某一點的偏導數，那麼正切值就等於它在這個點的偏導數：tanθ=∂f/ ∂x。那麼，原來的波動方程就可以寫成這樣：

這裏我稍微解釋一下偏導數的符號，我們用∂f/ ∂x表示函數f(x,t)的偏導數，這是一個函數，x可以取各種各樣的值。但是如果我加一個豎線|，然後在豎線的右下角標上x+Δx就表示我要求在x+Δx這個地方的導數。

再來看一下這個圖，我們已經約定了A點的橫座標為x，對應的角度為θ；B點的橫座標是x+Δx，對應的角度為θ+Δθ。所以，我們可以用x+Δx和x這兩處的偏導數值代替θ+Δθ和θ這兩處的正切值tan（θ+Δθ）和tanθ，所以波動方程才可以寫成上面那樣：

接着，如果我們再對方程的兩邊同時除以Δx，那左邊就變成了函數∂f/ ∂x在x+Δx和x這兩處的值的差除以Δx，這其實就是∂f/ ∂x這個函數的導數表達式。也就是説，兩邊同時除以一個Δx之後，左邊就變成了偏導數∂f/ ∂x對x再求一次導數，那就是f(x,t)對x求二階偏導數了。

上面我們用我們已經用∂²f/ ∂t²來表示函數對t的二階偏導數，那麼這裏自然就可以用∂²f/ ∂x²來表示函數對x的二階偏導數。然後兩邊再同時除以T，得到方程就簡潔多了：

把方程左邊的tan(θ+Δθ)-tanθ變成了函數f(x,t)對空間x的二階偏導數，這個過程非常的重要，大家可以好好體會一下這個過程。正切值tanθ就是一階導數，然後兩個正切值的差除以自變量的變化就又產生了一次導數，於是總共就有了兩階，所以我們才能得到上面那個簡潔的式子。

08 經典波動方程

再看看方程右邊的μ/T，如果你仔細去算一下T/μ的單位，你會發現它剛好就是速度的平方，也就是説如果我們把一個量定義成T/μ的平方根，那麼這個量的單位剛好就是速度的單位。可以想象，這個速度自然就是這個波的傳播速度v：

這樣定義速度v之後，我們最終的波動方程就可以亮相了：

這個方程就是我們最終要找的經典波動方程，為什麼把它作做經典的波動方程呢？因為它沒有考慮量子效應啊，在物理學裏，經典就是非量子的同義詞。如果我們要考慮量子效應，這個經典的波動方程就沒用了，我們就必須轉而使用量子的波動方程，那就是大名鼎鼎的薛定諤方程。

薛定諤就是從這個經典波動方程出發，結合德布羅意的物質波概念，硬猜出了薛定諤方程。這個方程讓物理學家們從被海森堡的矩陣支配的恐懼中解脱了出來，重新回到了微分方程的美好世界。薛定諤方程雖然厲害，但是它並沒有考慮狹義相對論效應，而高速運動（近光速）的粒子在微觀世界是很常見的，我們也知道當物體接近光速的時候就必須考慮相對論效應，但是薛定諤方程並沒有做到這一點。

最終讓薛定諤方程相對論化是狄拉克，狄拉克把自己關在房間三個月，最終逼出了同樣大名鼎鼎的狄拉克方程。狄拉克方程首次從理論上預言了反物質（正電子），雖然當時的科學家們認為狄拉克這是在胡鬧，但是我國的物理學家趙忠堯先生卻幾乎在同時就首次在實驗室裏觀測到了正負電子湮滅的情況。

另外，狄拉克的工作也推動了量子場論的誕生，打開了一扇讓人無比神往的新世界大門。物理學家們沿着這條路馴服了電磁力、強力、弱力，建立起了粒子物理的標準模型，於是四海清平，天下大定，除了那該死的引力。這些精妙絕倫的故事我們後面再講，如果把這些故事寫成一本《量子英雄傳》，嗯，一定不比金庸的武俠遜色~

好了，迴歸正題，看到這個經典波動方程到後面還能掀起那麼大的浪來，是不是突然就對它肅然起敬了呢？我們這樣一頓操作推導出了經典波動方程，有的朋友可能有點懵，沒關係，我們再來捋一下。這個看着很複雜的，包含了二階偏導數的方程其實就只是告訴我們：我們把這跟繩子極小的一段看作一個質點，那麼這個質點滿足牛頓第二定律F=ma，僅此而已。

09 復  盤

我們整個推導過程不過就是去尋找F=ma中的這三個量。我們把繩子的張力在豎直方向做了分解，然後得到了它在豎直方向上的合力F（T·sin（θ+Δθ）-T·sinθ）；我們定義了單位長度的質量μ，然後就可以計算那小段繩子的質量m（μ·Δx）；我們通過對波的函數f(x,t)的分析，發現如果對這種表示距離（位移）的函數對時間求一次偏導數就得到了速度，再求一次偏導數就得到了加速度，於是我們就得到了這段繩子的加速度a（∂²f/ ∂t²）。然後我們就把這些量按照牛頓第二定律F=ma拼了起來。

在處理問題的過程中，我們做了很多近似：因為我們是取得很小的一段，那麼我們就可以用Δx近似代替繩子的長度Δl；假設擾動很小，繩子偏離x軸很小，那麼角度θ就很小，我們就近似用正切值tanθ代替正弦值sinθ。很多人乍一看，覺得這麼嚴格的推導怎麼能這麼隨意的近似呢？你這裏近似那裏近似，得到的最終結果還是準確的麼？

要理解這個問題，就得正式去學習微積分了，我現在告訴你微積分的核心思想就是一種以直代曲的近似，你信麼？微積分裏就是用各種小段小段的直線去近似的代替曲線，但是得到的結果卻是非常精確的。因為我們可以把這些線段取得非常非常的小，或者説是無窮小，那麼這個誤差也就慢慢變成無窮小了。所以我們在分析這跟繩子的時候，也都強調了是取非常小的一段，給一個非常小的擾動，得到一個非常小的角度θ。

另外，tanθ就是一次導數，然後它們的差再除以一次Δx，就又出現了一次導數，所以方程的左邊就出現了f(x,t)對位置x的兩次偏導數。方程的右邊就是函數f(x,t)對時間t求兩次偏導數得到的加速度a（求一次導數得到速度，求兩次就得到加速度）。

所以，雖然我們看到的是一個波動方程，其實它只是一個變裝了的牛頓第二定律F=ma。理解這點，波動方程就沒什麼奇怪的了。我們再來仔細的審視一下這個方程：

這個波動方程的意義也很直觀，它告訴我們f(x,t)這樣一個隨時間t和空間x變化的函數，如果這個二元函數對空間x求兩次導數得到的∂²f/ ∂x²和對時間t求兩次導數得到的∂²f/ ∂t²之間滿足上面的那種關係，那麼f(x,t)描述的就是一個波。

如果我們去解這個方程，我們得到的就是描述波的函數f(x,t)。而我們前面對波做數學分析的時候得到了這樣一個結論：如果一個函數f(x,t)描述的波，那麼就一定滿足f(x,t)=f(x-vt,0)。所以，波動方程的解f(x,t)肯定也都滿足前面這個關係，這一點感興趣的朋友可以自己下去證明一下。

好了，經典的波動方程我們就先講到這裏。有了波動方程，你會發現我們通過幾步簡單的運算就能從麥克斯韋方程組中推導出電磁波的方程，然後還能確定電磁波的速度。

本文經授權轉載自微信公眾號“長尾科技”。

特 別 提 示

1. 進入『返樸』微信公眾號底部菜單“精品專欄“，可查閲不同主題系列科普文章。

2. 『返樸』開通了按月檢索文章功能。關注公眾號，回覆四位數組成的年份+月份，如“1903”，可獲取2019年3月的文章索引，以此類推。