特殊的畫蛋技巧,國外網友想不出原理好捉急 | 科學DIY_風聞
把科学带回家-把科学带回家官方账号-专注于孩子的科普教育2019-12-30 20:33
【本文由公眾號“把科學帶回家”提供,ID:steamforkids】
馬上要過元旦了,想不想要一份特別的富含營養的元旦禮物呢?
今天就教大家2種變蛋方法:用圓造蛋,和用線造蛋。總之,隔壁小鳥網站上的網友已經看呆了,有近萬人點贊666。
下方一位想不出原理的網友留言得到了排名第三的點贊,他好捉雞。
翻譯:花了整整2分鐘想要搞明白這個動圖怎麼做的,橢圓是怎麼畫出來的。頭好暈啊。
我們一起來幫幫他吧!
關鍵概念
橢圓,圖西雙圓
材料和操作
紙
手
圓造蛋
1 首先,製造出一張圓形的紙。(可用圓規畫)

2 在圓裏隨便什麼地方點上一點。

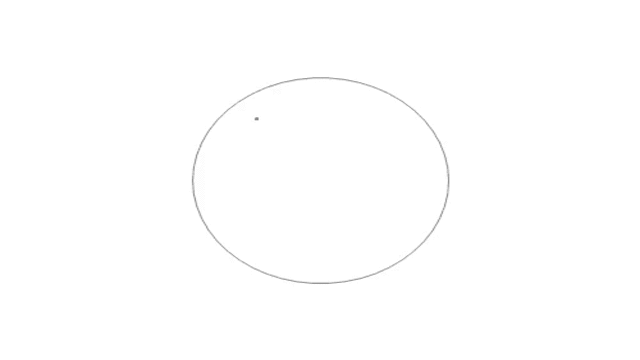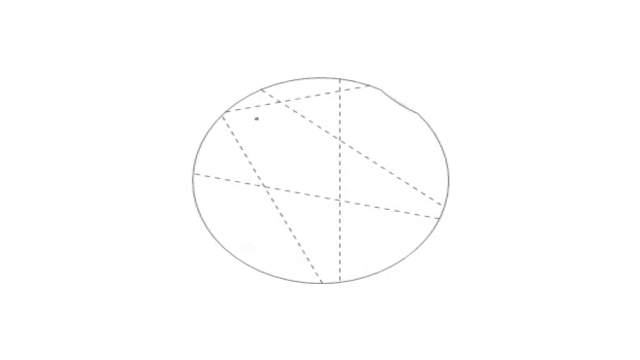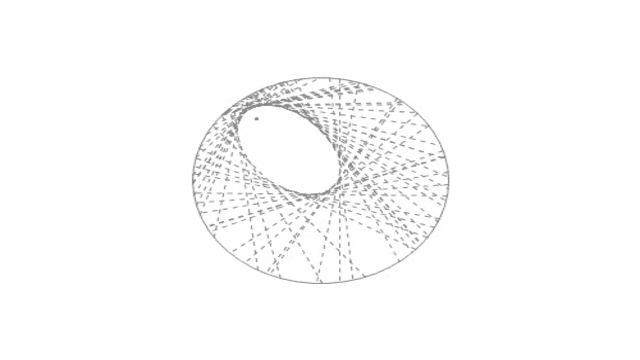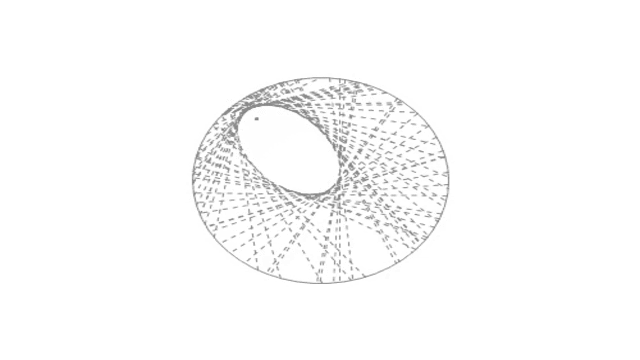
3 隨便折一條讓圓邊通過這個點的直線,反覆多次操作,像這樣子——


最後你就可以得到一個蛋了。

如果你是手殘黨,可以在下面的地址玩一玩——
當然,我們不僅可以用圓來畫蛋,還可以用圓做各種奇怪的事。
比如,如果在圓外隨便點一點,然後也同樣操作,掃出來的圖案就是一個雙曲線。
你可以點下面的網址玩一玩——
https://www.geogebra.org/m/VCNReSnS
啥也不磨機蛋
當然,畫橢圓還有更舒爽的方法。
比如這個搖起來很舒服的的機械。啊對了,這個小工具也叫啥也不幹機 (do-nothing machine),啥也不磨機(nothing grinder)。

嗯,光看它的運動,相信它沒有虧待自己的名字。
但是呢,別小看啥也不磨機哦,它可以把直線運動轉化為橢圓運動。
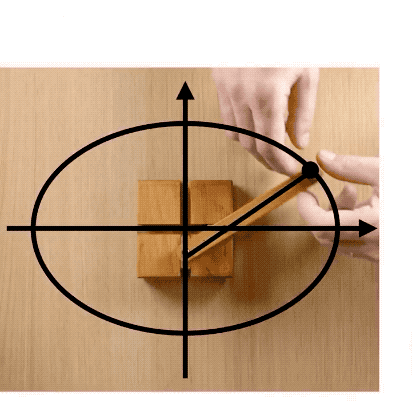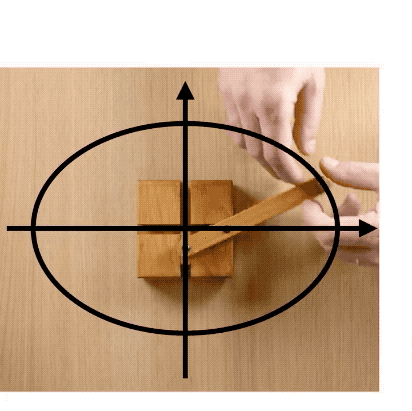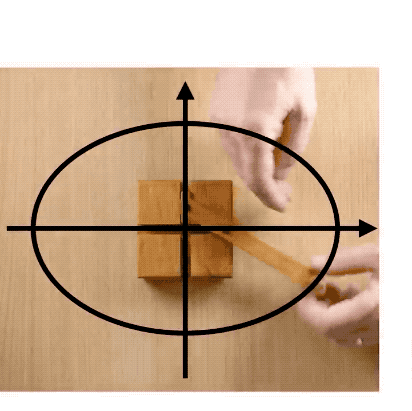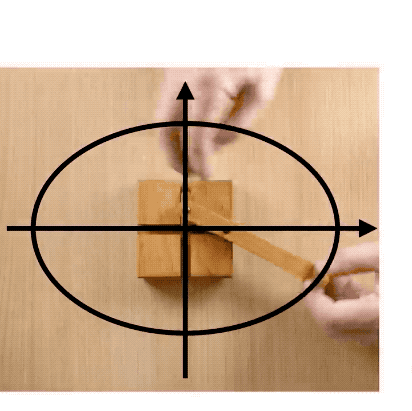
啥也不磨機還有更復雜更酷炫的變種,它也可以畫蛋蛋——

這麼好玩的啥也不磨機怎麼做呢,準備一些積木,膠水和木條,二軸的版本就可以了@ludic science
原理
圓造蛋
要從數學上證明折出來的圖形是橢圓很簡單。
假設圓心是A,你隨便點的那個點是S,過S這個點的隨便折的線和圓的交點是P。
現在呢,作SP的中垂線,和AP交於M。
很容易就可以證明,AM + MS = AM + MP = r,也就是圓的半徑。
這有什麼意義呢?
還記得橢圓的性質嗎?
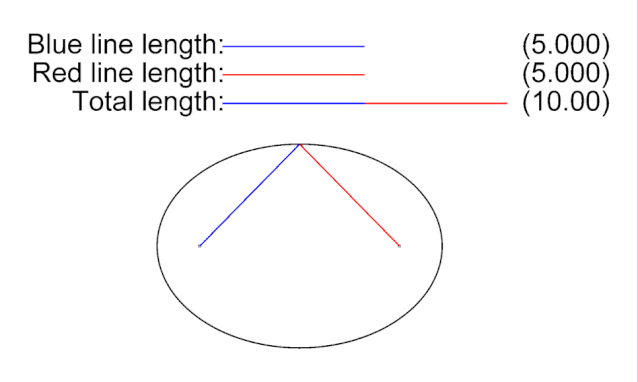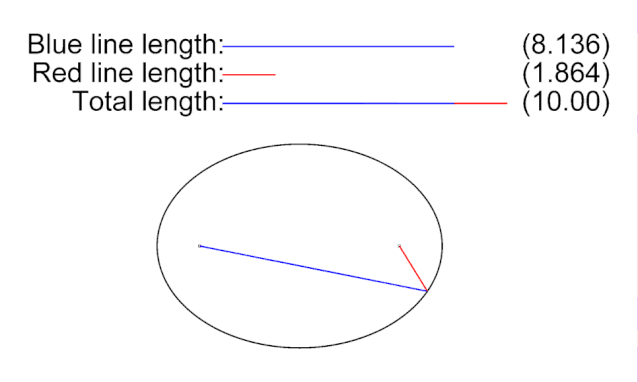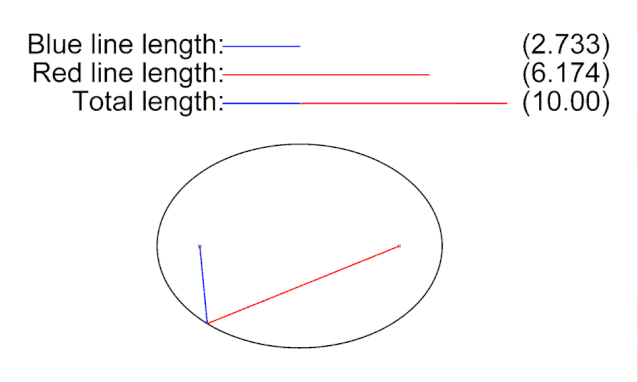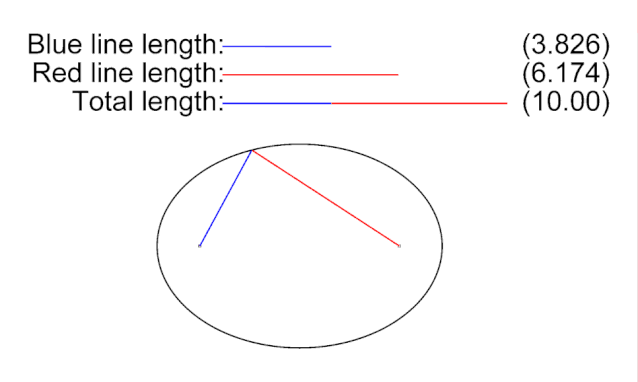
把一條繩子定住2個點,畫出的圖形就是橢圓。所以,我們只要證明AM+MS是一個固定值就可以了。我們剛剛不就證明了這點嗎?
很顯然,這條過M的中垂線掃出的區域,恰好就是一個橢圓,而且這個橢圓的長軸長度恰好等於圓的半徑。
啥也不磨機蛋
雖然被人叫做啥也不磨機,但是在計算機出現前,啥也不磨機有個正經的名字,叫做橢圓規(Ellipseograph),它是一個機械繪圖機哦。
William Ford Stanley and Co. Ltd公司在1880年左右製造的橢圓規,發明者是英國人Edward Burslow
@americanhistory.si
只要調整動點的長短,就可以畫出不同形狀的橢圓。
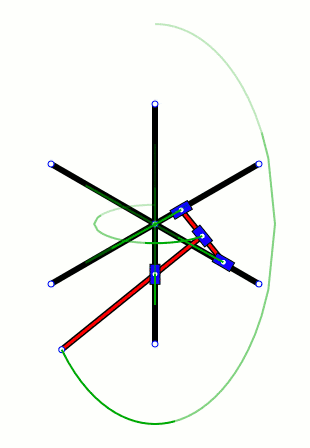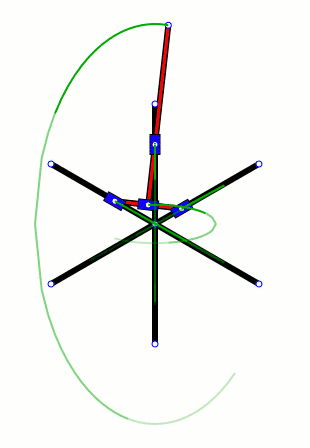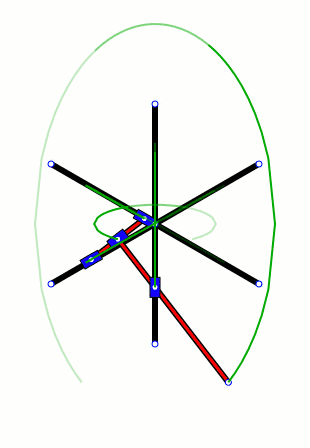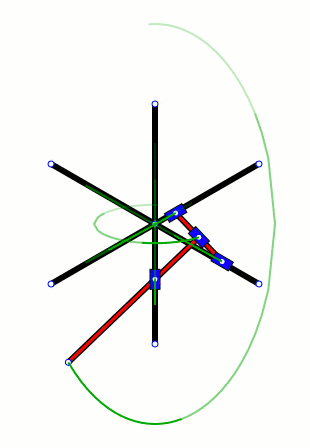
如果在啥也不磨機的杆子上畫上小點,就會看到它的不同部分掃出的不同圖形。不過有意思的是,總有2個點似乎在同一個小圓裏運動,但是它們各自又在做直線運動。好奇怪啊。
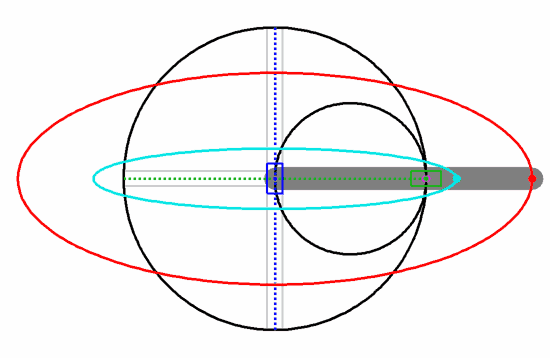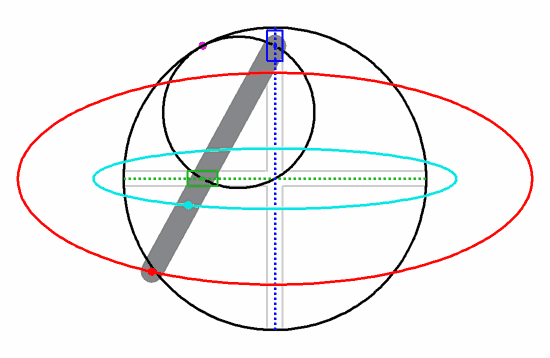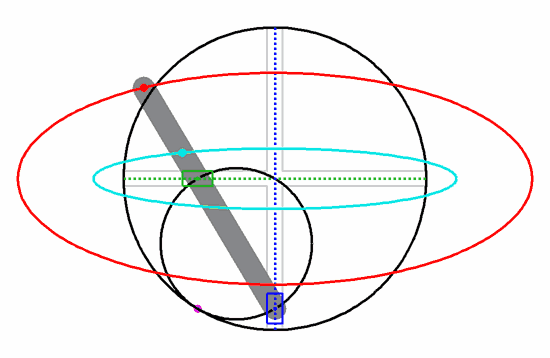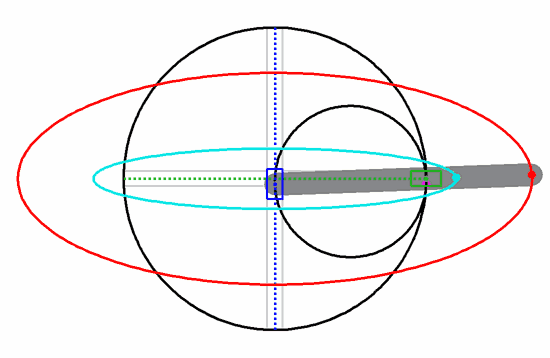
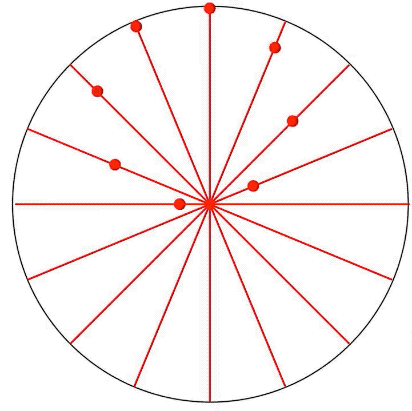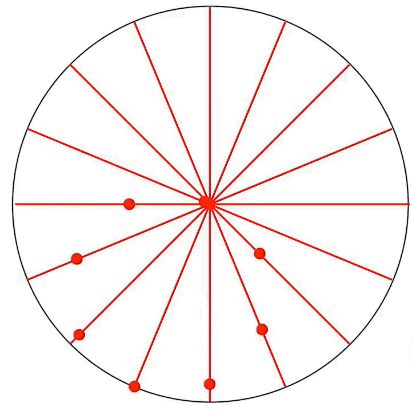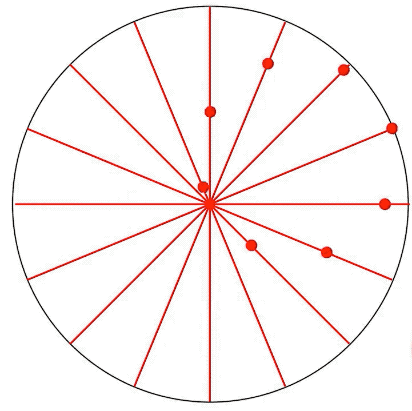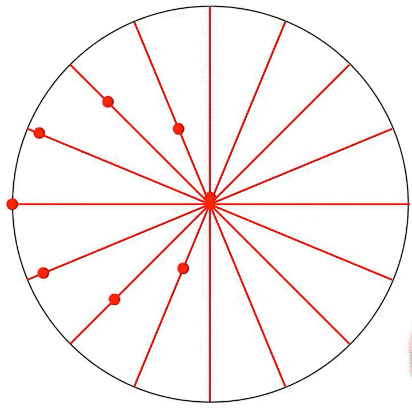
啥也不磨機的數學原理,叫做圖西雙圓(Tusi couple)。它是兩個直徑差一倍的圓形成的圖案。仔細觀察下圖,你就會發現,小圓上的任意一點都在做直線往復運動。
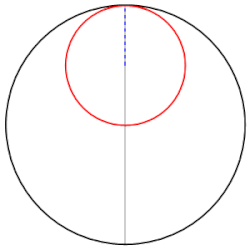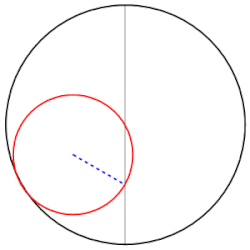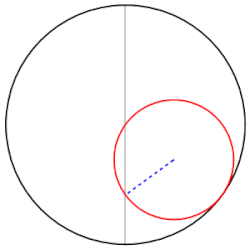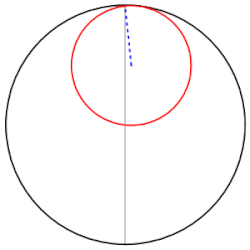
圖西雙圓
如果你不信,看看下面這個在網上把許多網友逼瘋的圖,實際上它就是個圖西雙圓,每個彩色的點都在做直線往復運動,同時也是一個圓的一部分。

但是小圓內(非圓的邊緣)除了圓心以外的任意一點,卻在做橢圓運動。圓心做的是圓周運動。
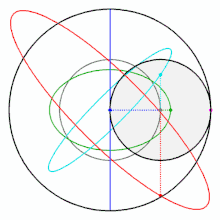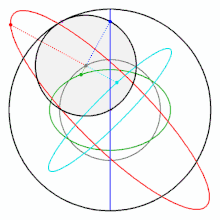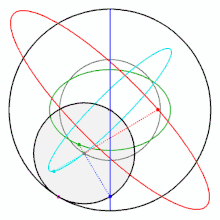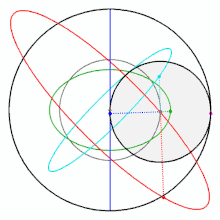
圖西雙圓是13世紀的波斯(今伊朗)的天文學家和數學家納西爾丁·圖西(Nasir al -Din al-Tusi)發現的。
伊朗在1976年發行的紀念圖西的郵票
@wikipedia
當時圖西想用這種運動來解釋內側行星(軌道在地球內側繞行的太陽系行星)的運動。實際上,哥白尼的《天體運行論》(De revolutionibus orbium coelestium)中有些模型(如水星模型)和圖西雙圓極為相似,因此有不少人認為哥白尼通過某種途徑參考了阿拉伯經典。
其實,圖西雙圓是一種特殊形式的內旋輪線(hypotrochoid)。
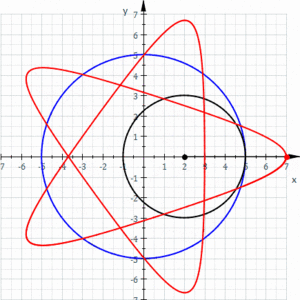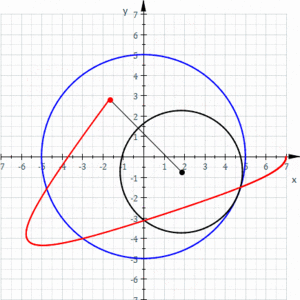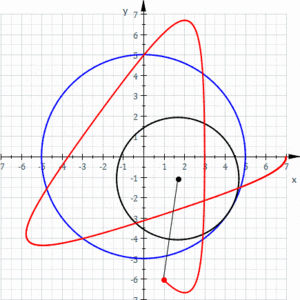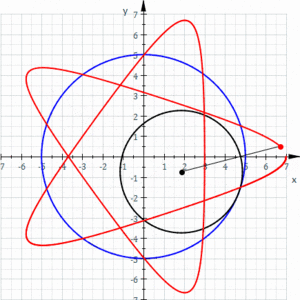
內旋輪線
玩過經典玩具萬花尺的小朋友對內旋輪線應該很熟悉了。

- 小明,你的科技小製作做什麼?
- 啥也不做機。
- 小明啊,啥也不做也就罷了,叫老師雞就不對了哦。






