看到風聞有人發“疫情與指數函數”的文章，自己覺得挺有意思嘗試解釋一下_風聞

如題，看到這樣一個帖子。

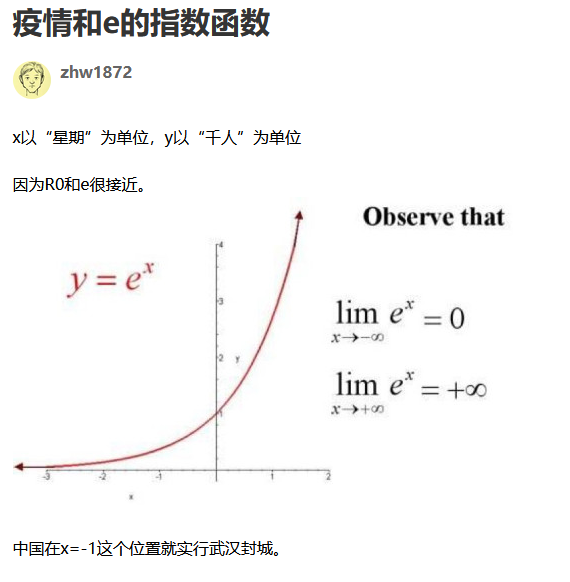
評論區有人回覆不理解為什麼會有這樣的發展趨勢，引起我的興趣，看看自己有沒有辦法解釋一下。

高中生物書裏肯定有關於J型曲線和S型曲線的説法，我不太記得當初有沒有從細節上説過這兩個曲線為什麼是這樣的形狀了。如果僅從數學的角度來説，假設時刻t感染病毒的人數為x(t)，那麼過了一段時間T以後，肯定有x(t+T)人感染，大概是下面這樣的方程

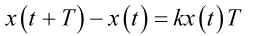
這個方程應該挺好理解的，t+T時刻感染的人，等於t時刻感染的人加上T時間新增的人數。這個新增的人數，最簡單的模型就是和時間T成正比，同時和t時刻人數成正比，比例係數取k。當然，這個模型還不太嚴謹，畢竟T時間內新增的人數本身又會傳染給健康的人。

上面這個方程，如果T足夠小，就可以得到下面這樣的微分方程

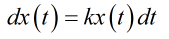
這個方程比上面那個嚴謹一點，很小一段時間內，增量可以認為只和t時刻感染人數，以及這麼小段的時間成正比。無非就是感染人數的增長率與當前感染人數成正比

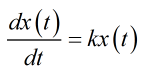
這個微分方程可以解，你有經驗可以直接看出這個就是指數函數。或者麻煩一點，變成下面這樣的表達式

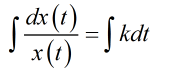
解出來就是這樣的表達式

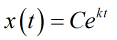
C是某個常數，你可以理解為它是用來修改曲線的形狀的。這個就是指數函數，很明確，底數就是自然對數e。至於評論區有人説，任何底大1的指數函數圖形都會趨於無窮這一點，老實説我想不到有什麼可能底數不會是e，希望有懂的人能夠解釋一下。如果你看過有關自然對數e話題的文章，他會告訴你這個是跟“增長”高度相關，原因就是這個方程。

接下來考慮更細緻一點的問題。傳染病一個很容易考慮到特徵就是，正在發病的人本身不會被人傳染。極端一點説，如果所有人都被感染（且未接受治療），那麼會有就不會再有新的感染髮生。數學上的處理使用下面這樣的方法。首先，人羣當中沒有被感染的人數是

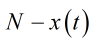
N是總人數。沒有被感染的人佔總人數的比例就是

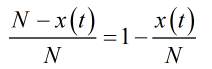
假如感染者平均分佈在人羣當中（實際上不可能），由於已經感染的人不會被感染，那麼極短時間dt內x(t)個感染者將帶來比前面指數模型更少的人，依據比例就是

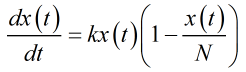
這個叫Logistic方程，神經網絡經常用的東西。它的解是

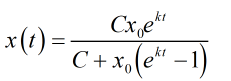
x0是x的初值，你也可以理解為它是用來修改曲線形狀的。這個解是比較常見的S型曲線，如果你對高中生物比較熟悉，可以很快回憶出它的一些特點。

這樣的思路可以建立更復雜的情況，比如説存在治療的情況

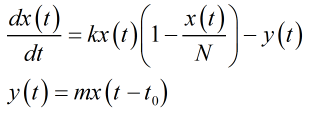
y(t)是t時刻的治癒人數，這裏假設所有人都只需要花t0天治療，且存活率為m，且都可能復發。

再考慮部分人獲得永久抗體不再復發的情況

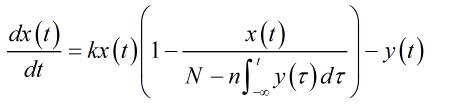
n為獲得永久抗體的概率。再考慮採取強制措施限制人員流動的情況

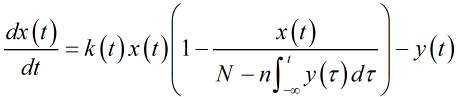
且k與時間成負相關（説明措施越來越嚴，且越來越有效，但更符合經驗的假設是它有個下限值，説明無論如何再嚴格，都總有些許可能導致增長）。實際上你會發現越來越複雜的情況，無非就是把模型裏的參數全部換成時變的，然後討論每一種措施對各個參數的影響，再求這個方程就好。

大致就是這樣。