宇宙是什麼形狀？_風聞

在我們的心中，宇宙似乎永遠存在。但利用幾何，我們可以探索各種三維形狀。正如彎曲的球面是平面地球的替代品，這些三維形狀也提供了“普通”的無限空間的替代品。

撰文****|********ERICA KLARREICH

譯者****|****** 我叫熊貓大俠**

來源：和樂數學

當你凝視夜空時，空間似乎朝着四面八方無限延伸。這是我們對宇宙的心智模型，但它不一定是正確的。畢竟，有一段時間，每個人都認為地球是平的，因為我們地球的曲率太微妙以至於無法探測到，球形的地球是不可思議的。

如今，我們都知道地球的形狀是一個球。但是我們大多數人很少思索宇宙的形狀。正如彎曲的球面是平面地球的替代品，其他三維形狀也提供了“普通”無限空間的替代品。

關於宇宙的形狀，我們可以提出兩個不同但又相互關聯的問題。一個是關於它的幾何：例如角度和麪積等精巧的局部測量。另一個是關於它的拓撲：這些局部部件是如何縫合在一起拼成一個整體形狀的。

宇宙學證據表明，我們能看到的那部分宇宙至少可以近似地認為是光滑而均勻的。空間的局部構造在每個點和每個方向上都是一樣的。只有三種幾何符合這種描述：平坦幾何、球面幾何和雙曲幾何。讓我們來探索這些幾何，還有一些拓撲考量，以及宇宙學證據表明哪個形狀最能描述我們的宇宙。

平坦幾何

這是我們在中小學學的幾何。三角形的內角和為180度，圓的面積為πr^2。最簡單的平坦的三維圖形的例子是普通的無限空間——數學家們稱為歐幾里得空間——但也有其他的平坦形狀需要考慮。

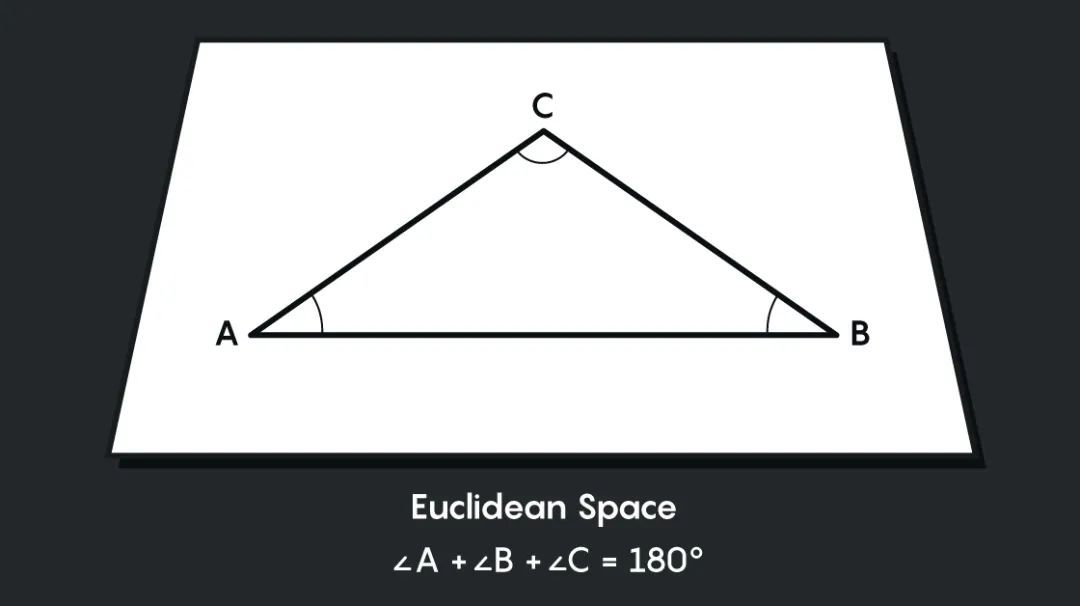這些形狀很難想象，但是我們可以通過二維來建立一些直覺。除了普通的歐幾里得平面外，我們還可以通過剪切平面的某些部分並將其邊緣粘在一起來創造其他平坦形狀。例如，假設我們剪下一張長方形紙，把它的對邊粘起來：把頂邊和底邊貼起來，我們得到一個圓柱體：

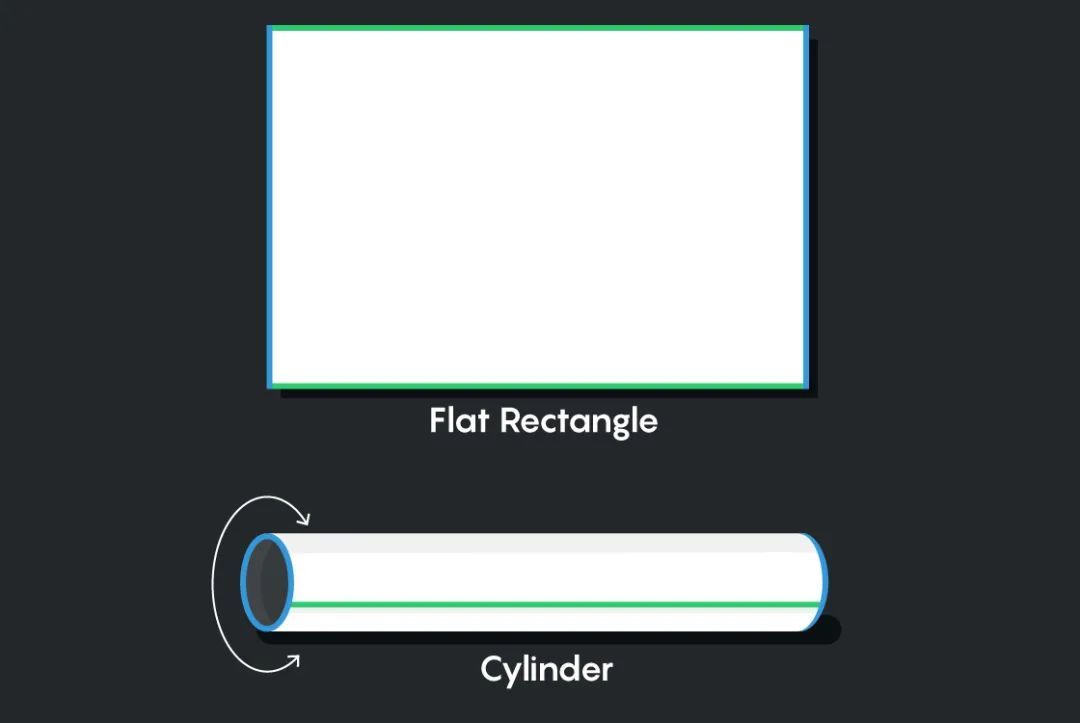接着可以把左右兩邊粘起來，得到一個“甜甜圈” (數學家們稱之為環面) ：

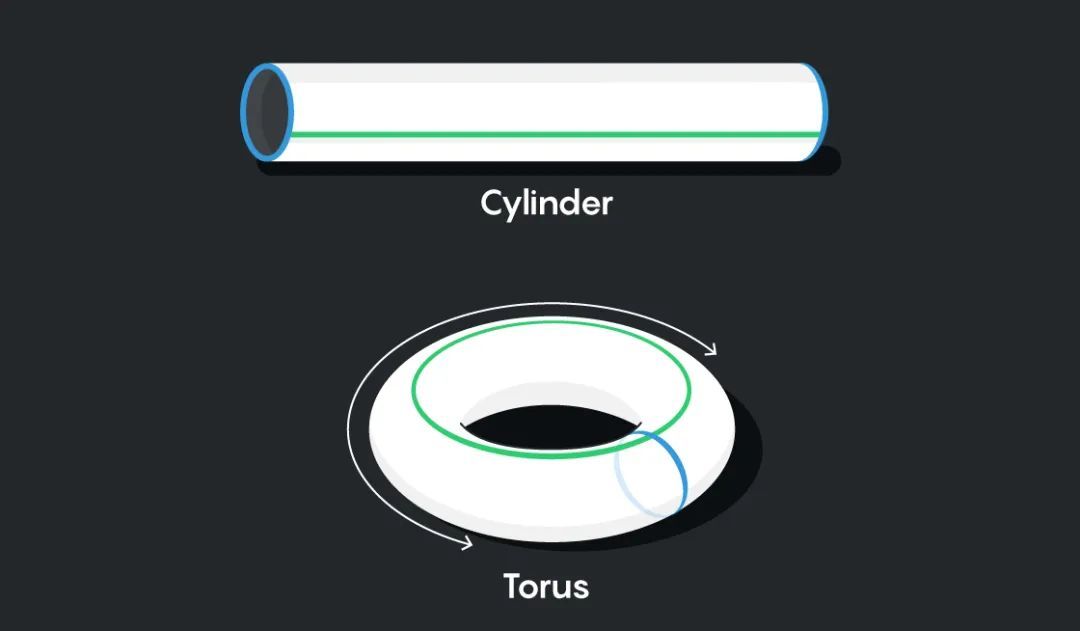現在，你可能會想，“在我看來這並不平坦”。你説的有點道理。我們在描述平坦環面時做了一點手腳。如果你真的想用這種方法用一張紙上做出一個環面，你會遇到困難。製作圓柱很容易，但是把圓柱的兩端粘起來是做不到的：環面內圈的紙會變皺，而外圈的紙不可能被拉得足夠長。你得用一些有彈性的材料來代替紙。但是這種拉伸扭曲了長度和角度，改變了幾何特徵。

在普通的三維空間中，沒有辦法在不扭曲平坦幾何特徵的情況下，用平面材料構建一個真實的、光滑的物理環面模型。但我們可以想象出生活在平坦環面上的感覺。

想象你是一個二維生物，它生活的宇宙是一個平坦環面。因為這個宇宙的幾何來自於一張平坦的紙，所有幾何事實都和平常一樣，至少在小範圍內是這樣的：三角形的內角和是180度，等等。但我們通過切割和粘貼使得拓撲結構發生了改變，這意味着生活在環面上的體驗將與我們過去習慣的感覺大不相同。

第一點：環面上有一些直線路徑可以繞一圈回到它們開始的地方：

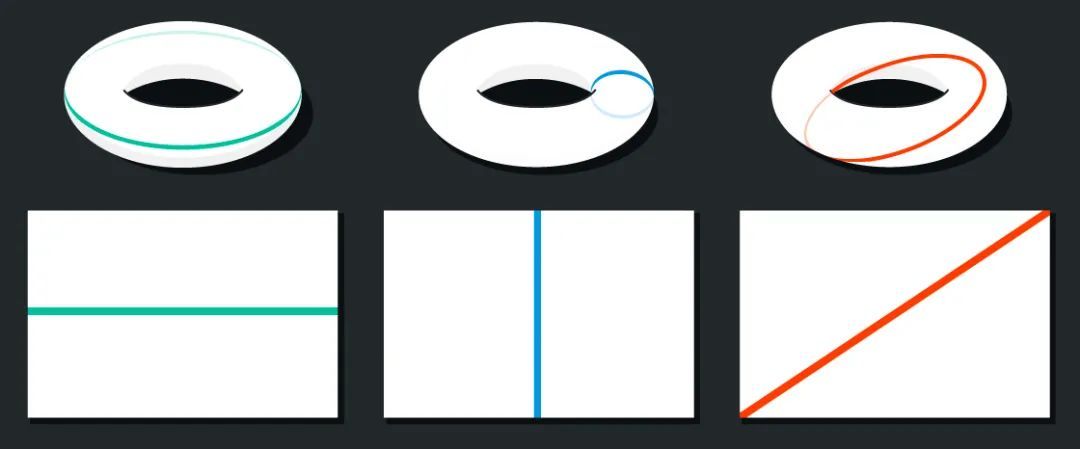這些路徑在環面上看起來是彎曲的，但是對於平坦環面上的居民來説，他們覺得它們是直的。因為光是沿着直線傳播的，如果你沿着某個方向向前看，你會看到你自己的後背：

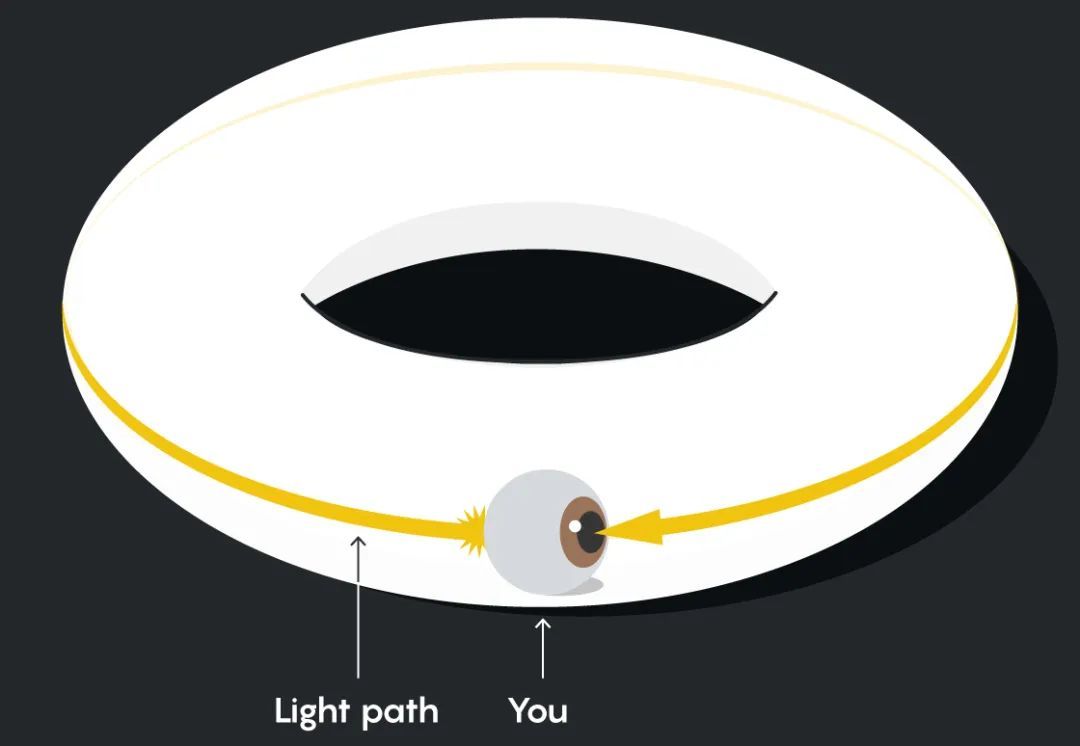在最初的那張紙上，你看到的光好像是從你身後來的，直到它照到左邊，然後又出現在右邊，就好像你在玩一個穿越式的電子遊戲：

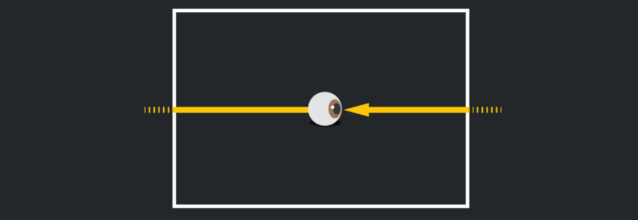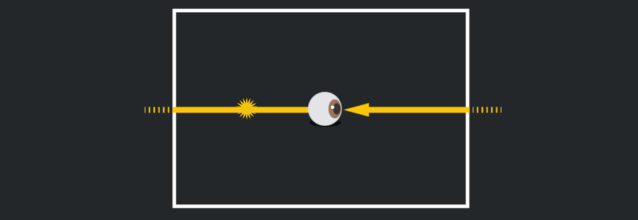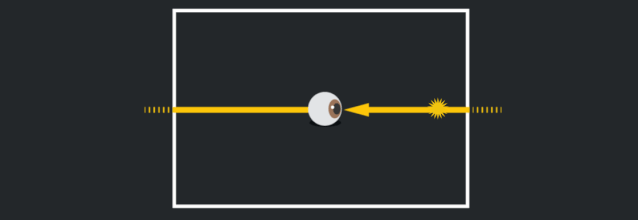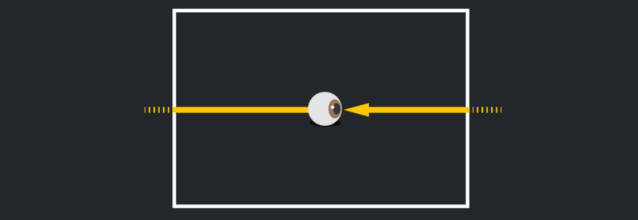
一個等價的思考方法是，如果你 (或一束光) 穿過四個邊的某一個，你會出現在一個新的“房間”裏，但實際上它們是同一個房間，只有了一個新視角。當你在這個宇宙中漫步時，你可以穿越到無數個你原來房間的複製房間裏。

這意味着你也可以從不同的方向看到無限多個不同的自己。這類似於你看大廳鏡子裏的自己，只是這裏你的複製品不是反射：

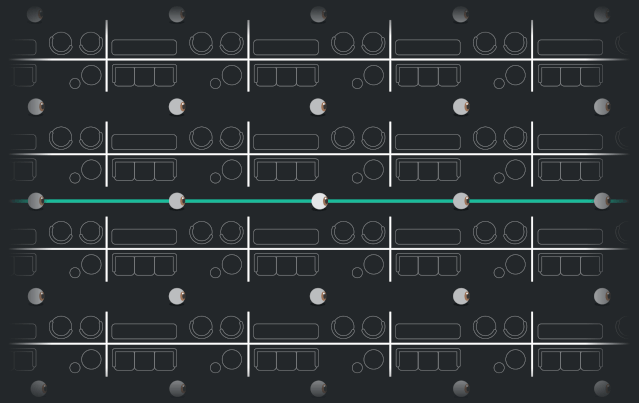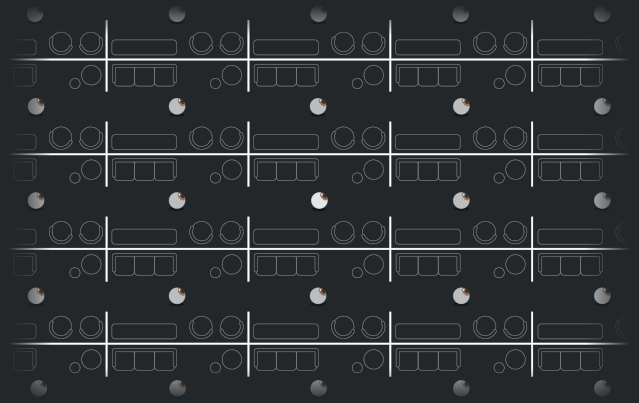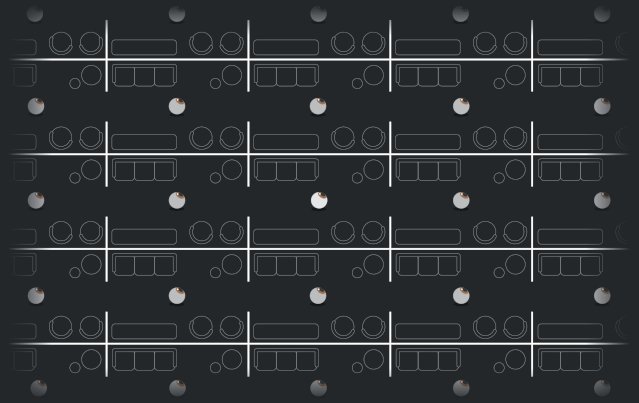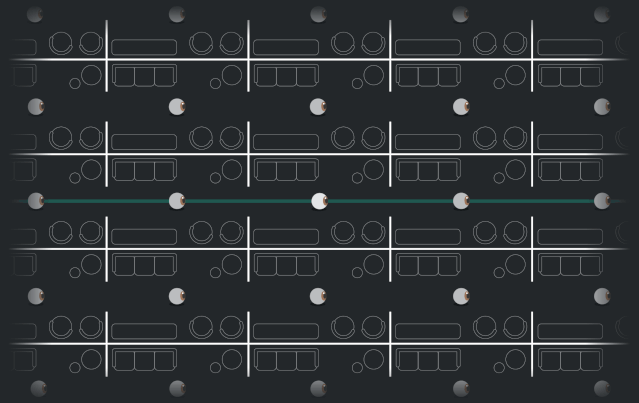
在甜甜圈上，它們對應着許多不同的迴路，通過這些迴路，光可以從你身後照回到你身上：

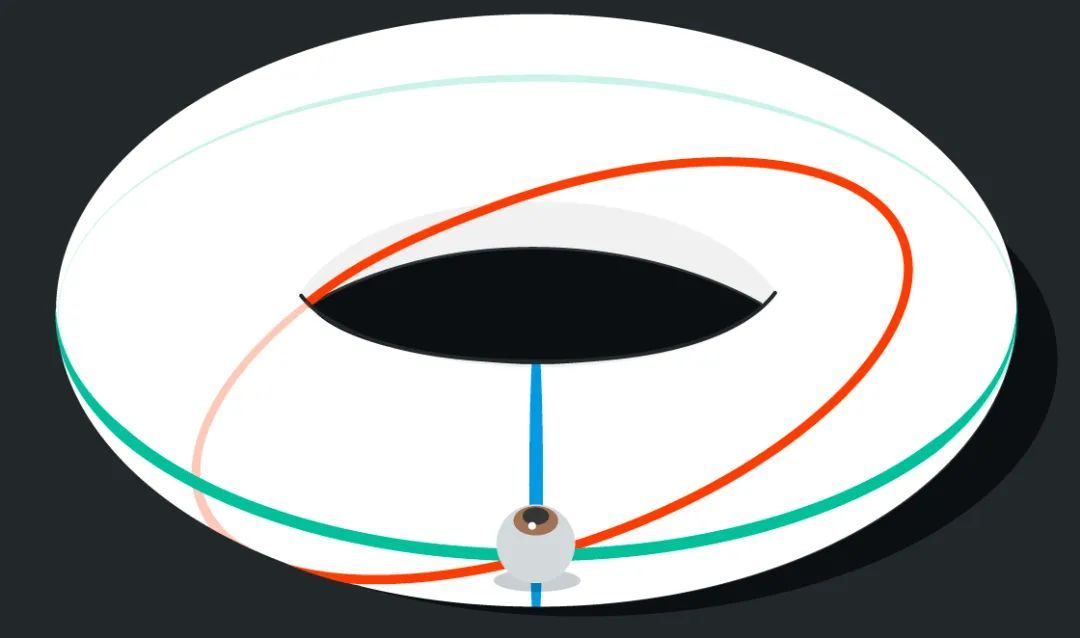類似地，我們可以通過粘住立方體或其他盒子的相對面來構建一個平坦的三維環面。我們不能把這個空間想象成普通無限空間中的一個物體——它根本就不在其中——但我們可以抽象地想象其中的生物。

就像二維環面中的生物生活在一個由無數個相同的矩形房間組成的二維方陣一樣，三維環面中的生物就像生活在一個由無數個相同的立方體房間組成的三維方陣中。你會看到無數個你自己的複製品：

三維環面只是10個不同的有限平坦世界中的一個。也有無限的平坦世界，如無限圓柱的三維類似物。在每個世界裏，都有不同的大廳鏡子的陣列供您體驗。

我們的宇宙是其他這些平坦形狀中的一種嗎？

當我們向太空望去，我們看不到無數個我們自己的複製品。儘管如此，要排除這些平坦形狀還是相當困難的。首先，它們都具有與歐幾里得空間相同的局部幾何性質，因此任何局部測量都無法區分它們。

如果你確實看到了自己的複製品，那麼那個遙遠的圖像就會顯示出你(或者你所在的星系)在遙遠過去的樣子，因為光線要經過很長時間才能到達你那裏。也許我們看到的是我們自己無法辨認的複製品。更糟糕的是，你的不同的複製品通常和你有不同的距離，所以他們中的大多數看起來都不一樣。也許它們離我們太遠了，我們根本看不見。

為了克服這些困難，天文學家們通常不是尋找我們自身的複製品，而是尋找我們所能看到的最遙遠事物的重複特徵：大爆炸後不久遺留下來的宇宙微波背景輻射 (CMB) 。在實踐中，這意味着在CMB中尋找具有匹配模式的熱點和冷點的圓對，這表明它們實際上是從兩個不同的方向看到的同一個圓。

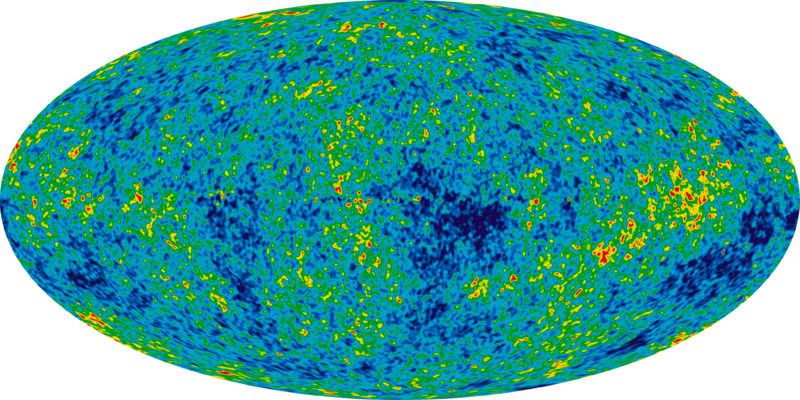
宇宙微波背景輻射。| 圖片來源：NASA/WMAP(2010)

2015年，天文學家利用普朗克太空望遠鏡得到的數據進行了這樣的研究。他們對數據進行了處理，尋找我們期望在平坦三維環面或另一種稱為slab的平坦三維形狀中看到的相匹配的圓，但他們沒有找到。這意味着，如果我們確實生活在一個環面上，它可能非常大，以至於任何重複的模式都在可觀測的宇宙之外。

球面幾何

我們都熟悉二維球面——一個球的表面，或一個橘子的表面，或地球的表面。但我們的宇宙是一個三維球面意味着什麼呢？

很難想象一個三維球面，但是通過一個簡單的類比可以很容易地定義它。就像二維球面是所有到普通三維空間中某個中心點的距離都相等的點的集合，三維球面是所有到四維空間中某個中心點的距離都相等的點的集合。

在三維球面上的生活和在平坦空間裏的生活感覺非常不同。為了感受一下，想象你是一個生活在二維球面上的二維生物。二維球面就是整個宇宙——你無法看到或進入周圍的任何三維空間。在這個球面宇宙中，光沿着最短的可能路徑傳播：大圓。對你來説，這些大圓就像直線。

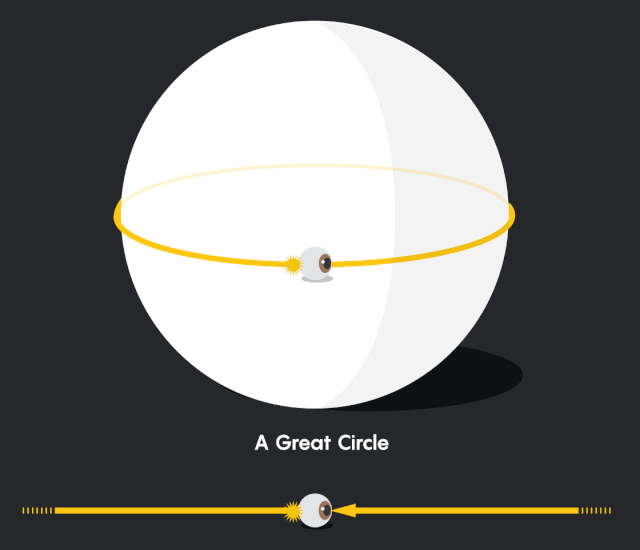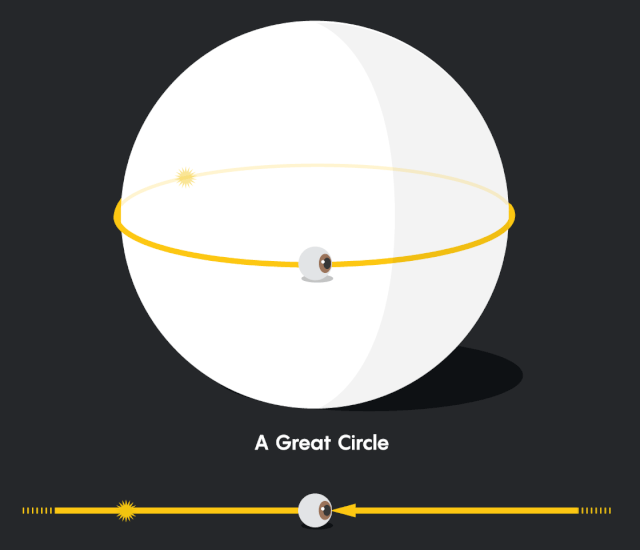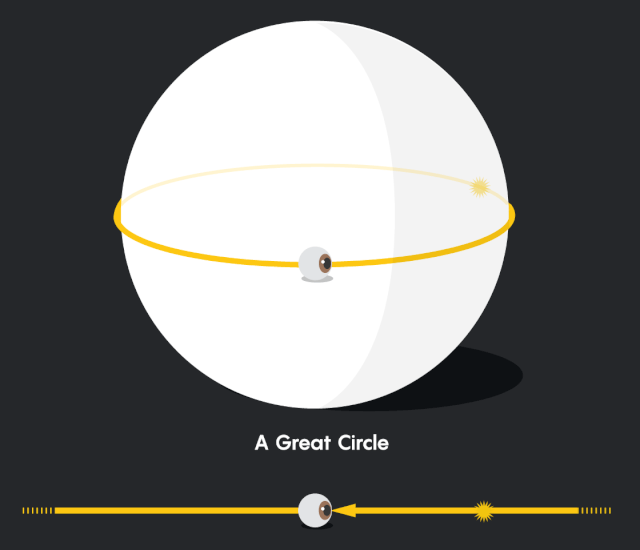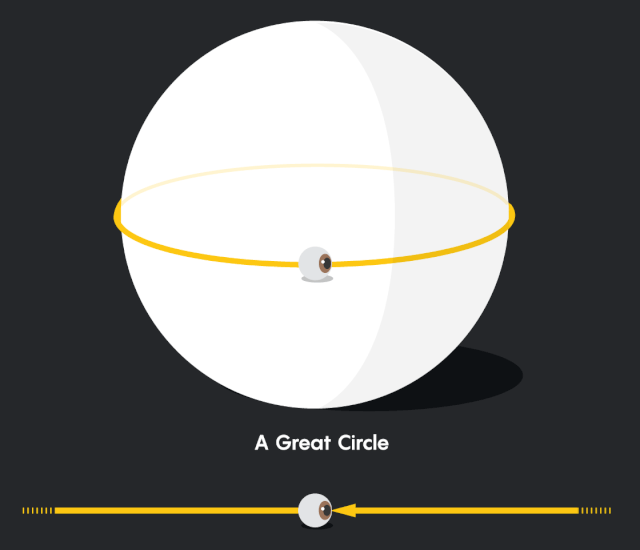
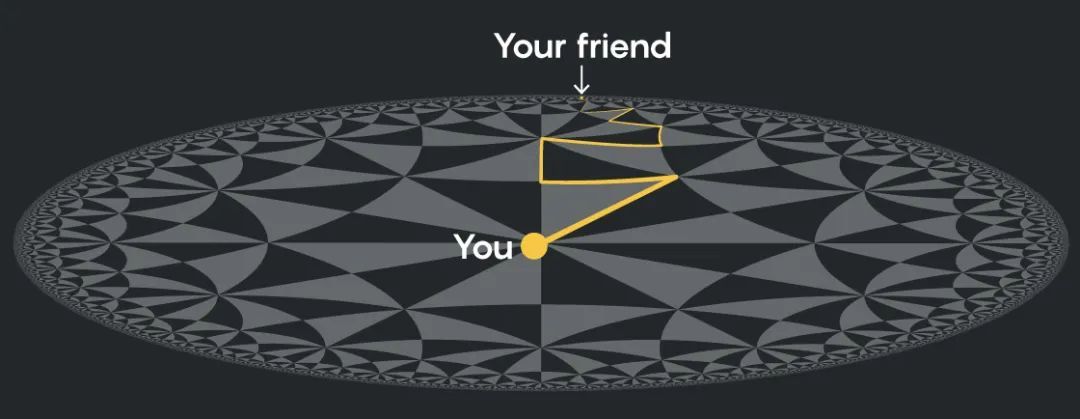
現在想象一下，你和你的二維朋友在北極點閒逛，你的朋友出去散步。當你的朋友走後，一開始他在你的視野裏會越來越小，就像在我們平常的世界裏一樣 (儘管他們不會像我們習慣的那樣迅速縮小) 。這是因為隨着你的視野範圍的擴大，你的朋友所佔的比例越來越小：

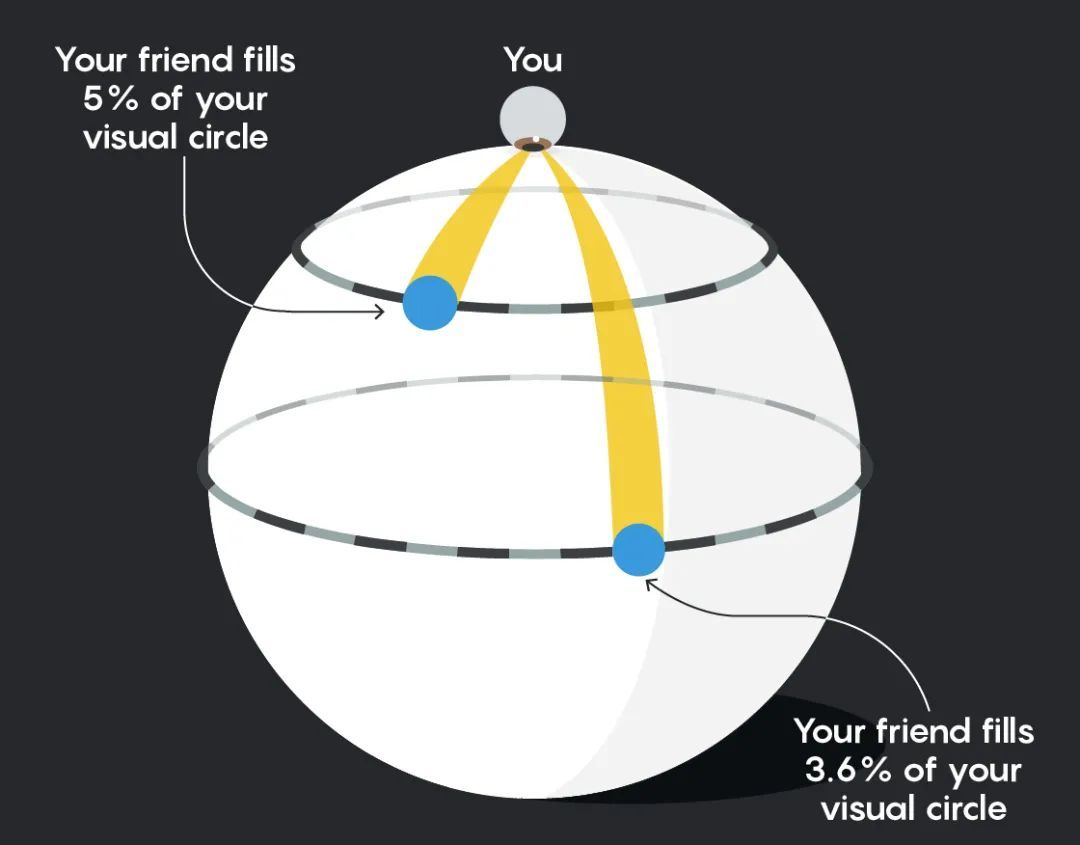但是一旦你的朋友越過赤道，奇怪的事情就發生了：他們離你越遠，看起來就會越來越大。這是因為他們在你的視野範圍內所佔的比例在增加：

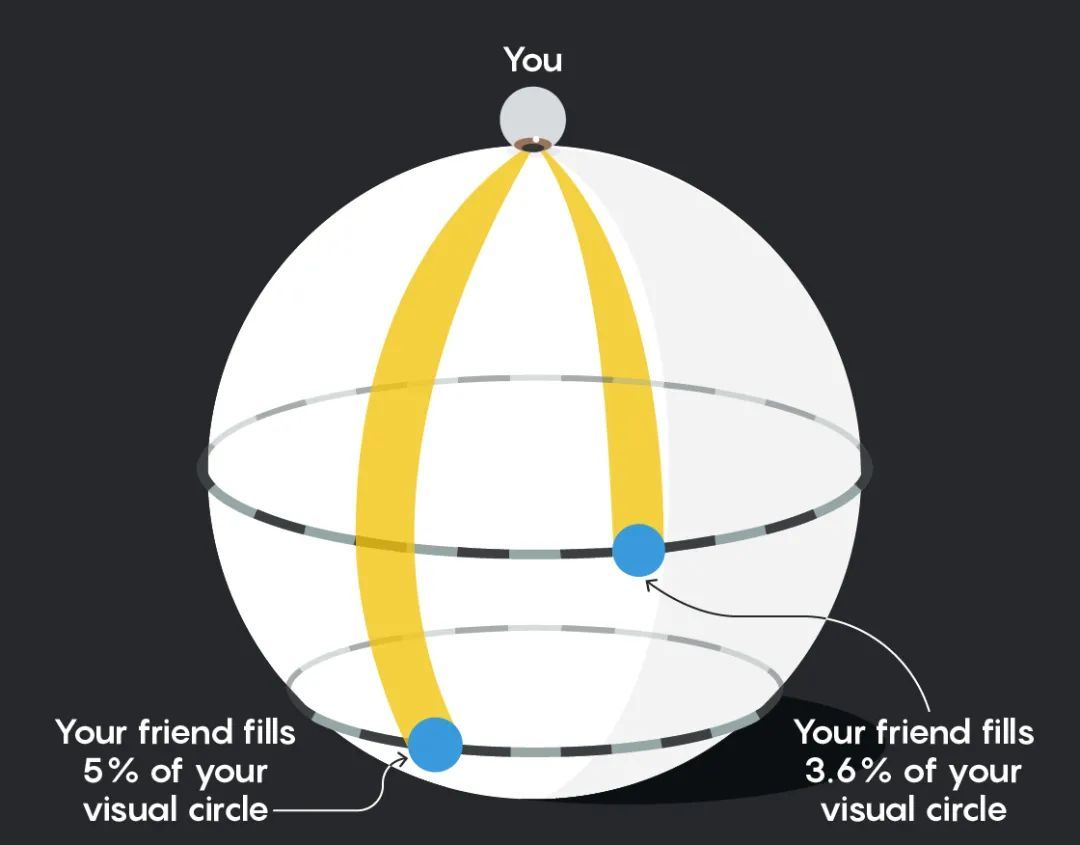當你的朋友離南極點只有10步遠的時候，他們看起來和離你10步遠的時候一樣大：

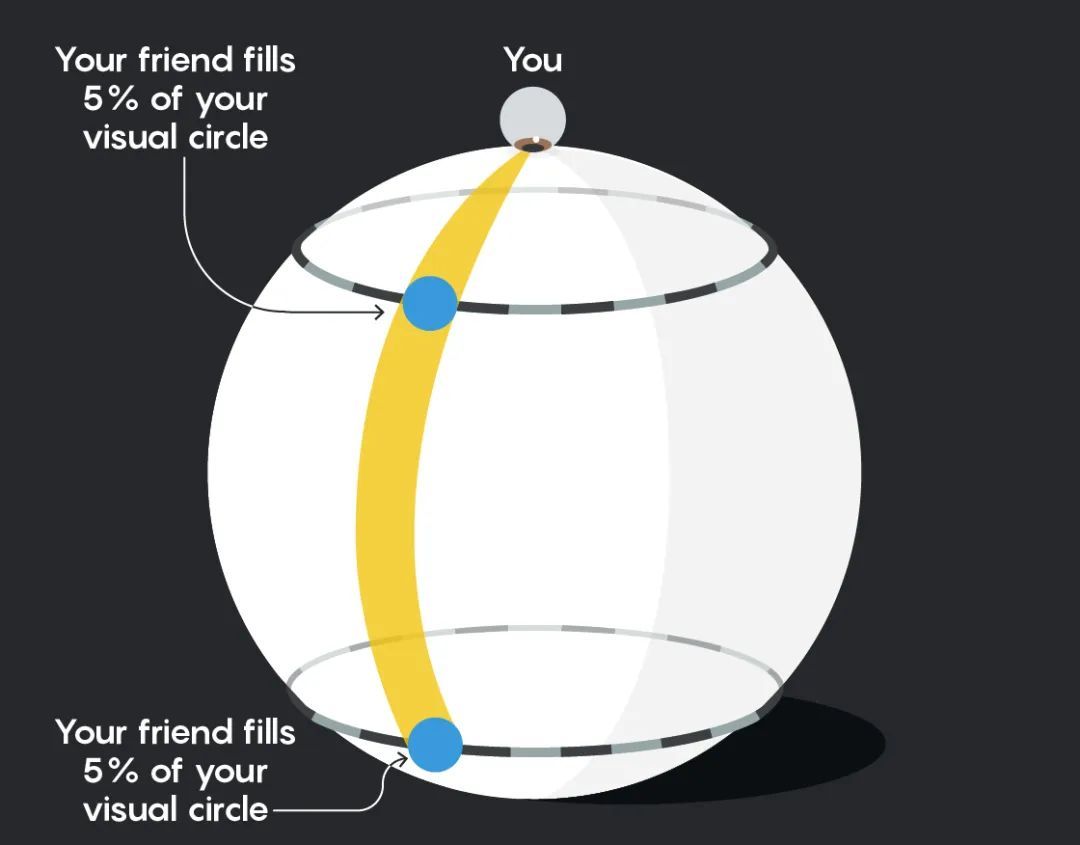當他到達南極點時，你可以從任何方向看到他，所以他填滿了你的整個視野：

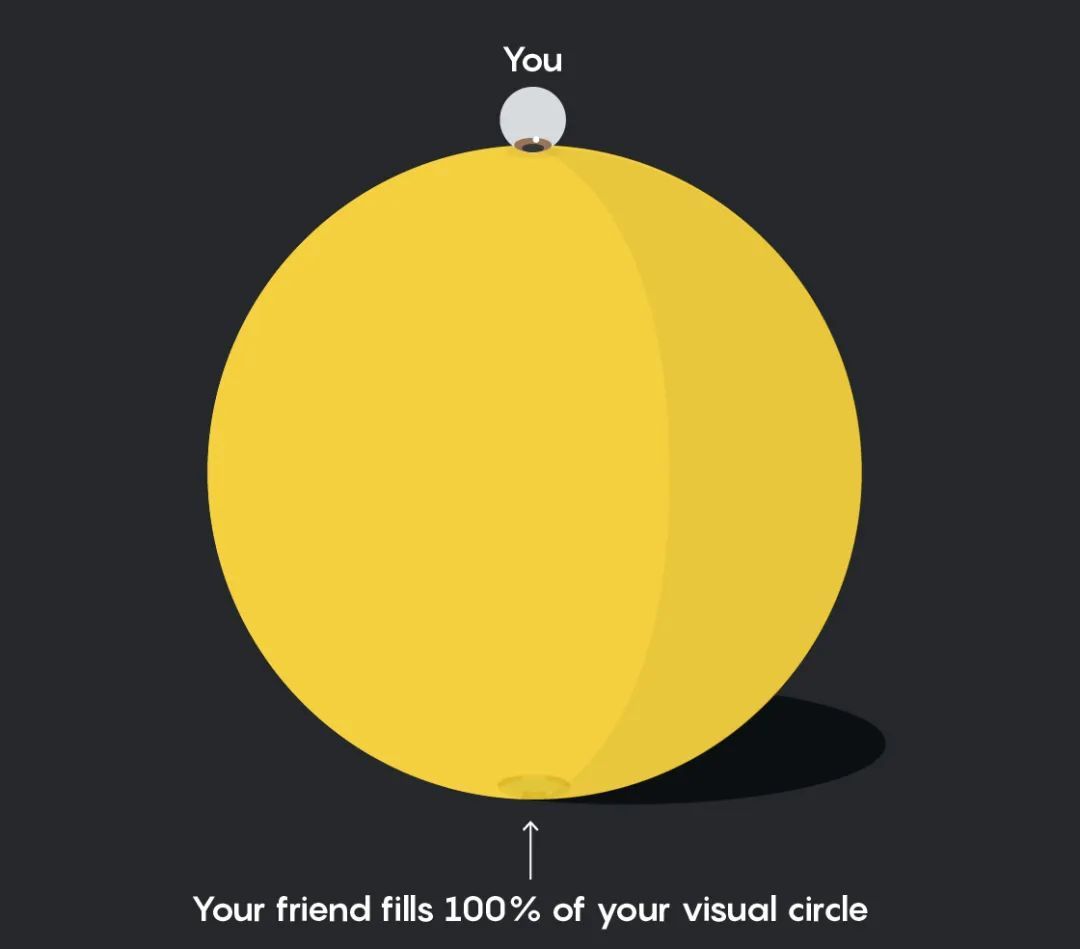如果南極沒有人，你看到的會變得更加奇怪：你會看到你自己。那是因為從你身上離開的光會繞着球面轉一圈，直到它回到你身上。

這可以直接推廣到三維球面中的生物。三維球面上的每個點都有一個相對的點，如果那裏有一個物體，我們看到的它就是整個背景，就好像它是天空一樣。如果那裏什麼都沒有，我們就會把自己當作背景，就好像我們的外貌覆在一個氣球上面，然後從裏到外膨脹成整個視野範圍。

雖然三維球面是球面幾何的基本模型，但它並不是唯一的這種空間。就像我們從歐幾里得空間中切出一塊並將其粘合在一起來創造不同的平坦空間一樣，我們也可以通過粘合三維球面中適當的部分來創造球面空間。與環面一樣，每一個粘在一起的形狀都有大廳鏡面效果，但在這些球面形狀中，只有有限個房間可以穿越。

我們的宇宙是球面空間嗎？

即使是最自戀的人也不會把自己作為整個夜空的背景。但是就像平坦環面一樣，我們沒有看到某種現象，並不意味着它不存在。球形宇宙的周長可能比可觀測宇宙的周長還大，這使得背景離我們太遠而看不見。

但與環面不同的是，球形宇宙可以只通過局部測量來探測。球面形狀與無限歐幾里得空間的區別不僅在於它們的整體拓撲結構，還在於它們的精細幾何結構。例如，因為球面幾何中的直線是大圓，所以三角形比歐幾里得的三角形更膨脹，內角和超過180度：

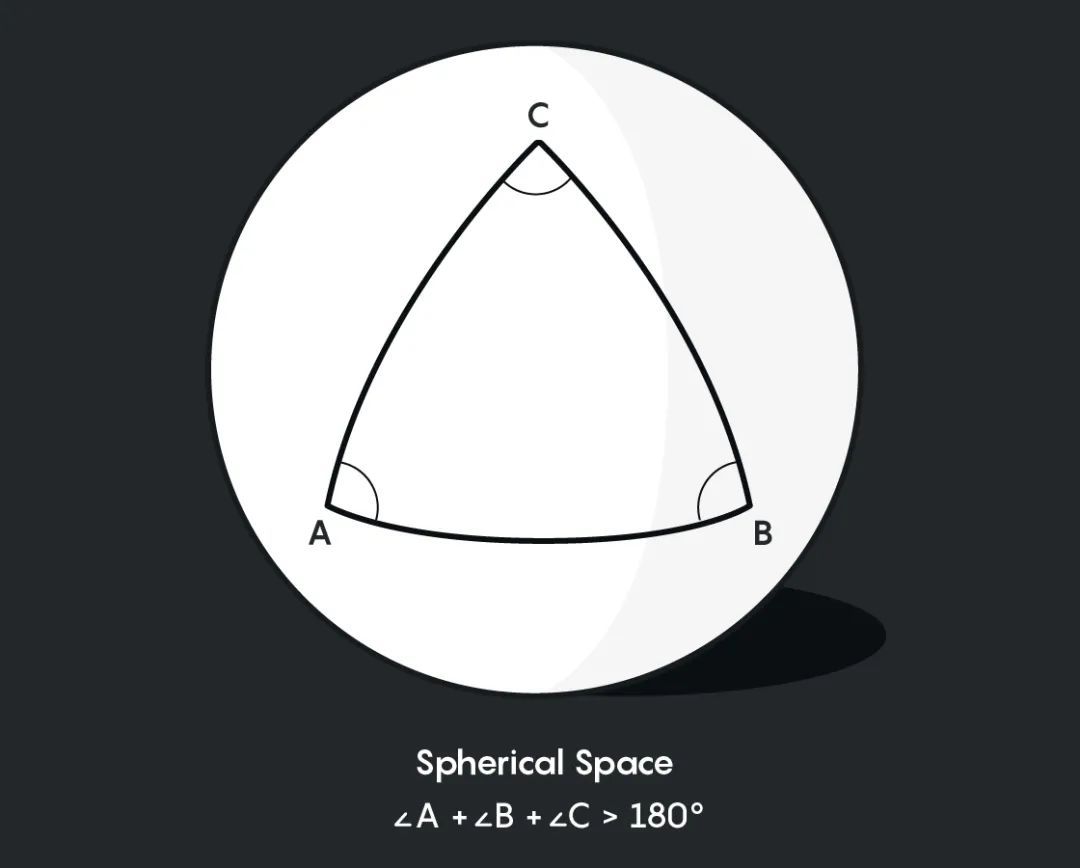事實上，測量宇宙中的三角形是宇宙學家檢驗宇宙是否彎曲的基本方法。對於宇宙微波背景中的每一個冷點或熱點，它的直徑和它到地球的距離都是已知的，這可以形成了一個三角形的三條邊。我們可以測量這些弧在夜空中的角度——即三角形的三個角之一。然後我們可以檢查邊長和角度的組合是否符合平坦幾何、球面幾何或雙曲幾何(其中三角形的內角和小於180度)。

大多數這樣的測試，連同其他的曲率測量，表明宇宙要麼是平坦的，要麼非常接近平坦。然而，一個研究團隊最近提出（https://www.quantamagazine.org/what-shape-is-the-universe-closed-or-flat-20191104/），普朗克空間望遠鏡2018年發佈的某些數據指向這是一個球形宇宙，儘管其他研究人員反駁説，這一證據很可能是統計上的僥倖。

雙曲幾何

不像球面本身是向內彎曲的，雙曲幾何是向外張開的。它是軟帽子、珊瑚礁和馬鞍的幾何。雙曲幾何的基本模型是一個無限的空間，就像平坦的歐幾里得空間。但是由於雙曲幾何比平面幾何向外擴張的速度快得多，所以即使是二維雙曲平面也無法放置於普通的歐幾里得空間中，除非我們願意扭曲它的幾何特徵。例如，這是一個被稱為龐加萊圓盤的雙曲平面的變形圖：

從我們的角度來看，邊界圓附近的三角形看起來比中心附近的三角形小得多，但是從雙曲幾何的角度來看，所有三角形的大小都是一樣的。如果我們試圖使三角形的大小相同，也許要用有彈性的材料來製作圓盤，從中心向外讓每個三角形膨脹——我們的圓盤開始像一頂軟帽子，從中心向外會越來越彎曲。當我們接近邊界時，這種彎曲將會失去控制。

從雙曲幾何的角度來看，邊界圓與任何內點的距離都是無限遠的，因為你必須穿過無窮多個三角形才能到達那裏。雙曲平面向四面八方無限延伸，就像歐幾里得平面一樣。但就局部幾何而言，雙曲平面中的生活與我們習慣的非常不同。

在一般的歐幾里得幾何中，圓的周長與半徑成正比，但在雙曲幾何中，圓的周長與半徑成指數關係。我們可以看到，在雙曲圓盤邊界附近堆積的三角形數量呈指數增長。

由於這個特性，數學家們常説在雙曲空間中很容易迷路。如果你的朋友們在普通的歐幾里得空間中離你而去，他們看起來會越來越小，但變化很慢，因為你的視界並沒有增長得那麼快。但在雙曲空間中，你的視界呈指數級增長，所以你的朋友們很快就指數級縮小成小點。如果你沒有跟上你朋友們的步伐，你以後幾乎不可能再找到他們。

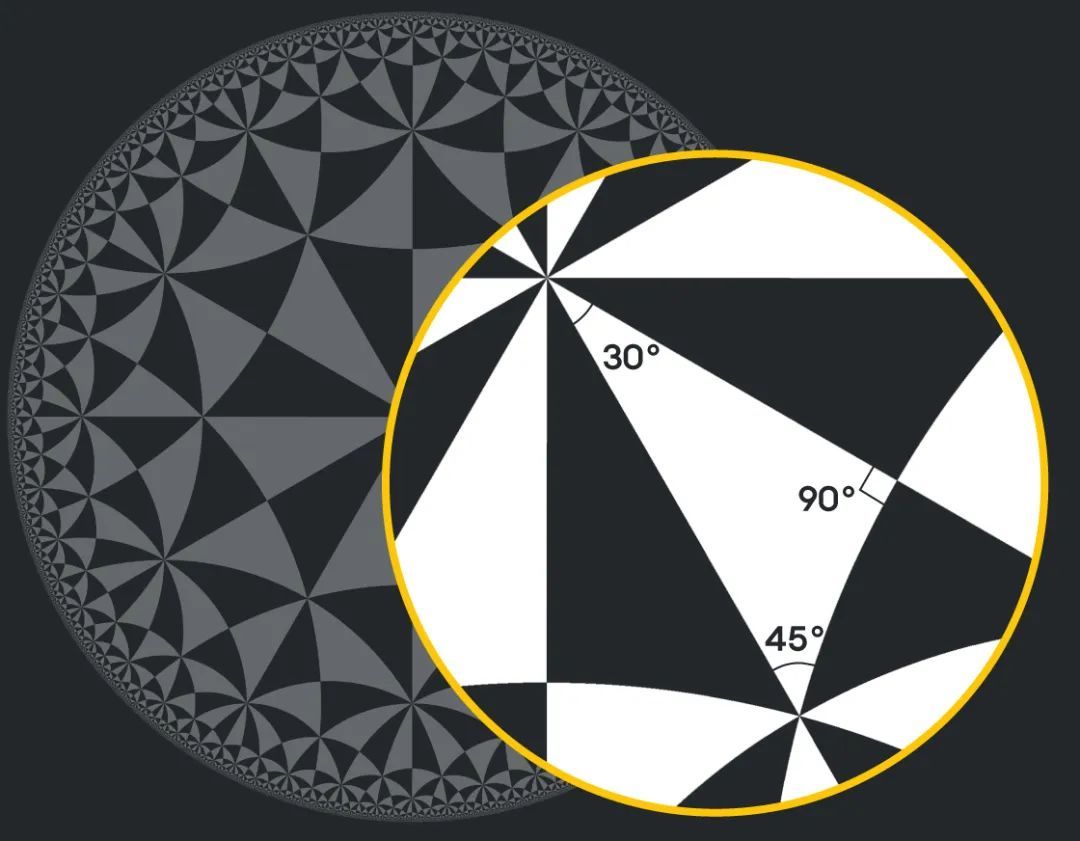
在雙曲幾何中，三角形的內角和小於180度，例如，在下圖中，三角形的內角和為165度：

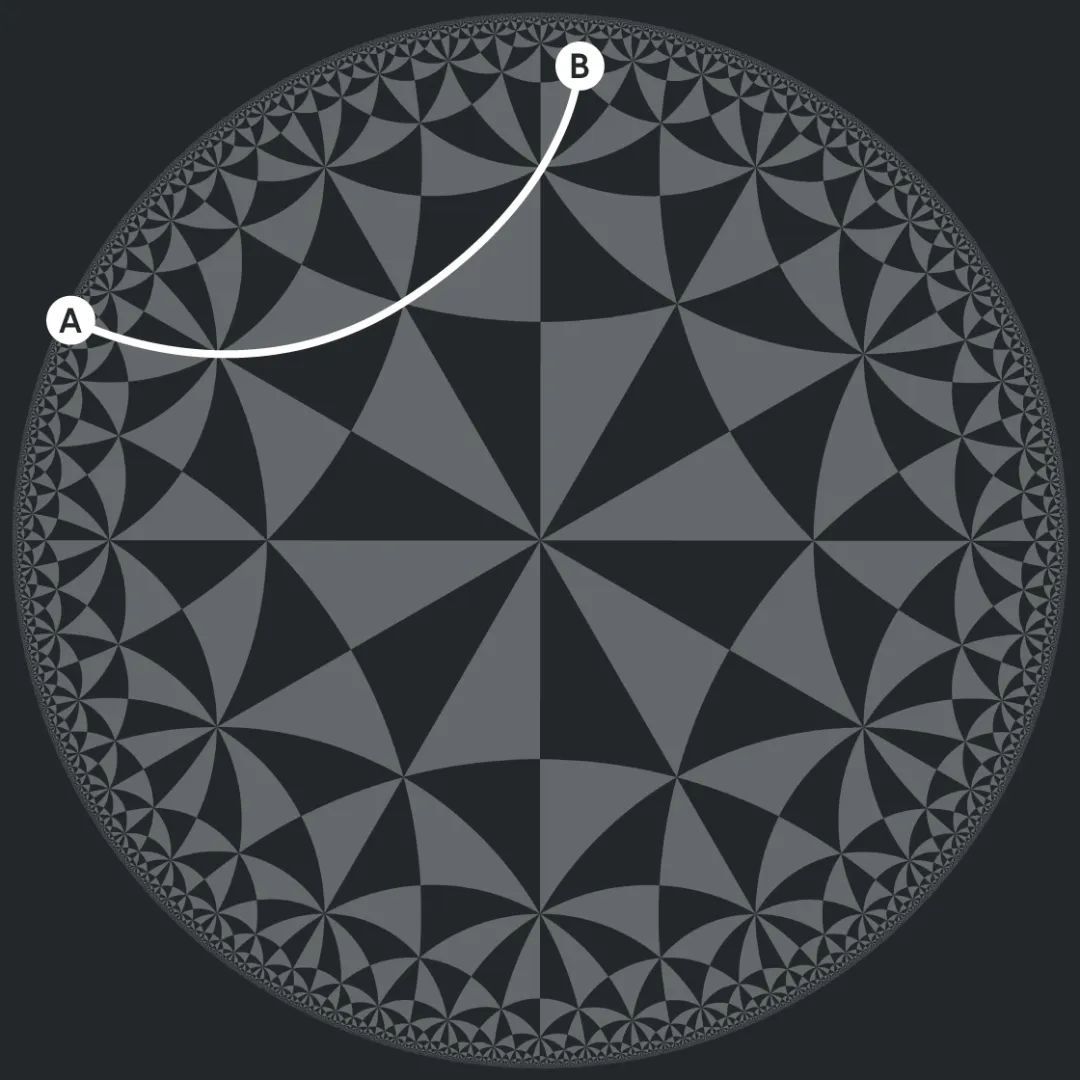
這些三角形的邊看起來不是直線，但這是因為我們通過一個扭曲的鏡頭來觀察雙曲幾何。對於居住在龐加萊圓盤上的人來説，這些曲線就是直線，因為從 A 點到 B 點最快的方式是走這樣一條捷徑：

有一種很自然的方法可以製作一個三維的龐加萊圓盤模型——只需製作一個三維球體，然後用三維形狀填充它，當它們接近邊界球面時，就會變小，就像龐加萊圓盤上的三角形一樣。就像平坦幾何和球面幾何一樣，我們可以通過切割和粘合三維雙曲球體的適當部分得到其他三維雙曲空間的組合。

我們的宇宙是雙曲空間嗎？

雙曲幾何，連同狹窄的三角形和指數增長的圓，似乎與我們生活的周圍空間的幾何不相符。事實上，正如我們已經看到的，到目前為止，大多數宇宙測量似乎都傾向於宇宙是平坦的。

但我們不能排除我們生活在一個球面世界或雙曲世界的可能性，因為這兩個世界在小範圍看起來幾乎是平坦的。例如，在球面幾何中，小三角形的內角和僅略大於180度，而在雙曲幾何中，小三角形的內角和僅略小於180度。

這就是為什麼早期的人類認為地球是平的——在他們能夠觀察到的尺度上，地球的曲率太小以至於無法探測。球面形狀或雙曲形狀越大，每個小塊就越平坦，所以如果我們的宇宙是一個非常非常大的球面形狀或雙曲形狀，我們可以觀察到的部分就會如此接近平面，其曲率只能期盼未來的超精密儀器來檢測。

本文經授權轉載自微信公眾號“和樂數學”。本文譯自：quantamagazine，原題：What Is the Geometry of the Universe?來源：https://www.quantamagazine.org/what-is-the-geometry-of-the-universe-20200316/

特 別 提 示

1. 進入『返樸』微信公眾號底部菜單“精品專欄“，可查閲不同主題系列科普文章。

2. 『返樸』提供按月檢索文章功能。關注公眾號，回覆四位數組成的年份+月份，如“1903”，可獲取2019年3月的文章索引，以此類推。