小學數學應該學什麼?_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2020-06-12 14:58
提要:
1 小學數學科學的唯一核心課題是自然數。
2 一個孩子的識數過程需要在數年時間中走完人類識數的漫長道路,這絕不可能是一個簡單容易的任務。
3 扳着手指數數具有超越多對象處理本能的重要意義。
4 一個好的數學教育者應該知道,加法的原始意義是兩個有限集的無交併的勢。
5 一個好的數學教育者應該明白,自然數集就是滿足皮亞諾公理的集合,而且應該理解自然數集的無限性,這是人對於無窮的第一個科學認識。
6 數學教育應按數學發展史順序進行,而不是按邏輯基礎來進行。
撰文 | 姜樹生
小學數學應該學什麼?這本來不是個問題,但近年來小學數學課程變化相當大,增加了很多內容且都是必修的,以致“減負”完全成了官腔;而小學數學原有的一些內容被弱化。在此背景下,“小學數學應該學什麼”成了很多人討論和爭議的問題。
1 先打個預防針
關於這個問題,常見的意見非常多,預期本文也會受到很多反駁。其實本文中的很多看法並非像數學那樣嚴謹的科學道理,反駁的意見可能更高明。但建議認真的讀者帶着批判的眼光有選擇地看,至少下面幾種用不着看:
1)生搬教條的
在文獻中有很多涉及數學教育的觀點,如“數學是研究數量關係和空間形式的科學”,“數學是對客觀現象抽象概括而形成的科學語言與工具”等等,這些觀點雖然不無道理但並不是嚴謹的科學定律。還有很多教學方法如“探索性學習”、“項目式學習”、“螺旋式上升”等等,也是不無道理但尚在嘗試。
但生搬教條者會把這些當成“聖旨”,每條都比數學更正確。這些人都是“政治掛帥”的,要求數學教育服從這些理論的指導,為此可以把數學教程改得一塌糊塗,但他們絕不會認錯的。
建議您把“政治正確”留給他們,您只要數學正確就可以了。
2)採用無定義術語的
這些人圍繞着一些沒有定義的術語討論不休,這樣的術語很多,如:
素質教育:對這個術語不僅沒有社會共識,也沒有權威的解釋,甚至沒有官方定義。高分低能:例如説有的學生考分高但不會換燈泡,但考試沒有換燈泡這一項,如果加上這一項如何呢?應試教育:是否有考試的教育就是“應試教育”?這樣的討論常常導致取消考試的主張。教育公平:我們只能説公民有平等的受教育的權利。但教育本身如何“公平”?有些人説這話的意思是“憑什麼你能上北大清華我就不能?”減負:學生負擔過重需要減輕,但需要先釐清什麼是過重。如果象商家先漲價再打折那樣,先加重負擔再減輕一些有意義嗎?不是説笑話,這樣的例子很多。例如先把上課時間提早半小時然後再改為晚半小時,或者取消給學生打分改為貼小紅旗小紅花等等。 很多教科書就是在“減負”的名義下越改越厚的(參看 [6])。奧數:這個詞來源於國際數學奧林匹克(IMO),但現在絕大多數人所説的“奧數”與 IMO 毫無關係,只是打着這個旗號搞培訓或競賽等,準確地應該稱為“偽奧數”。
數學有很多學科,即使在中學數學教程中也有代數、平面幾何、三角、立體幾何、解析幾何等多 個學科,但沒有一個“奧數”學科。一個家長把孩子送入“奧數班”之前,至少應該看看“奧數”教程講的是什麼,有什麼學術依據和標準,有什麼意義和用處。可惜大多數這樣的家長很官僚主義。
對每個無定義術語,都是各人有各人的理解,各唱各的調,甚至成了“定義之爭”。因此以這類無定義術語為題的討論都是純粹浪費時間。
3) “不假思索”的
這些人説話很多很快但不走腦子,例如説“數學是枯燥的、深奧的、抽象的”,或者“數學是存在於天上的純粹理型”,或者“數只是人腦子裏的東西”等等。很多説法是人云亦云。但如果深究,他們自己都不知道自己説的是什麼意思。
4) 妄議數學的
這些人對於數學的瞭解範圍很窄也很膚淺,而且都是很早期的(最新也是二百多年前的),但他們張口閉口數學如何如何,這樣就把他們所不懂的數學全部槍斃了。
5) 故意抬槓的
例如您剛説一句“數學是科學”,他立馬反駁説“數學不是科學”,而且搬出不知哪裏來的奇談怪論作為論據。其實他也未必相信自己的説法,只是為了顯示自己與眾不同而已。但這樣的抬槓容易蹭熱度、圈粉。
2 小學數學科學的唯一核心課題:自然數
現在講本文的主要觀點:小學數學,至少就數學科學而言,唯一必設的課題是自然數。
然而在小學數學課程標準(參看 [11])中所設的課題有四個方面:“數與代數”、“圖形與幾何”、“統計與概率”、“綜合與實踐”。我們現在來逐個細看。
1) “代數”是中學數學課程的內容,雖然近年來有些中學代數下放到小學,但不能因此就説它是小學數學。何況全國數學教育發展頗不平衡,很多地方還不能把代數下放到小學。
2) 關於圖形的科學,是從初中平面幾何開始的。小學數學教程中對於圖形的認識,基本上是科普性的,不平凡的主要是面積、體積的計算,實際上是作為數的一類應用題而設。
3) 統計與概率,即使在中學教程中也只是科普性的,而且現在中學數學教程中的概率並不比小學教程更深。
4) 小學數學中有很多應用題,這一方面是理解自然數的重要途徑,另一方面也是學會應用自然數的必要步驟。不過“綜合與實踐”説得含糊其辭。
有一點值得注意:在歷史上的任何一個時期,小學數學課程都不是很“專”的,即總有一些數學科學以外的內容,包括科普方面的內容、技術(早年是珠算,現在有計算器的使用等)、度量衡、法規(如科學記數法)等等。
那麼,課程標準所講的四個方面,除了“代數”有點疑問外,也沒有什麼錯啊?為什麼單強調“自然數”呢?
請注意另一點:除了自然數外,其他的內容在不同的歷史時期都是經常變化的,甚至將來有些會過時。但自然數是不會有變化更不會過時的。
另一方面,如果自然數沒學好,其他內容學得再好,小學數學也不能達標。
明白了這些,就知道在小學數學教學中永遠應該重點關注“自然數”,這也是小學數學最難的部分,教學上需要花的功夫也最大。反過來説,永遠不應該以其他方面的內容衝擊自然數的教學,或壓縮自然數教學的課時。
3 學習自然數的過程、目標和難點
然而,很多人覺得自然數沒什麼了不起,人人都識數。他們忘了自己當年的識數過程有多艱鉅,更不明白很多人一生都沒有完成識數過程。
數學是歷史最悠久的科學,而自然數是科學最早研究的對象。雖然考證很困難,但至少歐幾里得時代的文獻表明,在公元前 500 年人類已經完全認識自然數了。實際上人類認識自然數的過程可能有數萬年。而一個孩子的識數過程需要在數年時間中走完人類識數的漫長道路,這絕不可能是一個簡單容易的任務。
我們下面將小學生的識數過程做一個粗糙的分解,由此就可以看到其艱鉅性。
第一步:數(shŭ)十以內的數
幼兒首先學扳着手指數數,這是最早的數學實驗。
很多人會説:“這算什麼實驗呀?”現在固然有很精確的科學實驗手段,但不應菲薄老的實驗,因為科學是由此發展起來的。一百年前的生化實驗,在今天看來很粗糙;今天普通裝修隊配備的激光測距器,五十年前連尖端實驗室裏也沒有。而今天頂尖的實驗手段,將來也會被超越。我們下面將談到很多小學數學實驗,都是廣泛使用並且很有效的。很多人嫌它們簡單粗糙,但現在還很缺少嘗試發明更好的實驗手段的人。
“一定要扳着手指數數嗎?桌上有 3 個蘋果,一眼就看出來了,哪用得着扳着手指數?”
是的,高等動物有同時處理多個視覺對象的能力,不僅 3 個,多至 5 個甚至 6 個對象都可能“一眼就看出來”。但 10 個就太多了,而且扳着手指數是有順序的。
這裏涉及“自然數是什麼”這樣一個基本問題。僅有“1”是不能成為自然數的,至少還要有與 1 不同的;僅有 1 和 2 也還不行,因為 1 和 2 可以代表少與多,低與高,甚至黑與白,有與無,對與錯,更一般的矛盾,總之可以表達一個比特的信息。
就是説,有信息的世界就有 1 和 2。但 3 就不同了,超越了一個比特的信息。所以老子説“道生一,一生二,二生三,三生萬物”。對於古人和今天的幼兒,對 3 的理解是深且難的,開始時可能將 3 理解為“很多”。中國的成語和諺語中有很多“三”是“很多”的意思,如“三人成虎”、“三人行必有我師”等,這種現象在其他民族的語言中也常見。
如上所説,即使很聰明的大腦,對超過 6 個的對象也缺乏直接處理的能力,那麼處理“7”就常常是困難的任務了。因此很多民族的語言中有涉及 7 的諺語和故事,其中的“7”是“很多”的意思。
由此可見,扳着手指數數具有超越多對象處理本能的重要意義。
但對於數(shŭ)十以內的數,扳着手指數數只是要學的任務之一,至少還有兩個另外的任務:理解這些數的物理意義和學會語言交流。
對於語言交流很明白:既要會數數,也要會説一、二、三、四等(在母語中)。當然還需要認識數字符號,但一般是在識字之後。
而對於理解數的物理意義這個任務,很多教育者缺乏足夠的認識,甚至將其忽略。
具體説,要讓孩子在數數時,知道所數的可能是桌上的蘋果,也可能是面前的孩子,等等。就是要從“3 個蘋果”、“3 個孩子”等等得到“3”的概念。這並不容易,需要經過反覆學習才能達到。教育者對此需要有足夠的耐心。
一個有效的實驗方法是利用“一一對應”,例如讓 3 個孩子拿桌上的 3 個蘋果,每人拿一個,就看到一一對應了。
這第一步如果有所欠缺,以後就需要補上,而且這樣的欠缺可能導致質量差或效率低,不如先把第一步完全做好。
第二步:一百以內的數的認識
在這一步,扳手指實驗顯然已經不夠了,需要一些實驗工具(如小棒)。以往這被稱為“遊戲”,但現在很多人已經認識到這就是數學實驗,儘管仍很粗糙。
“按順序數”的習慣,在這一階段要進一步加強。但這還不夠,要理解這些較大的數的物理意義,需要初步學習加法。
桌上有兩堆蘋果,一堆有 5 個另一堆有 8 個,現在把兩堆合併,一共有多少個?這就是加法問題。一個好的數學教育者應該知道,加法的原始意義是兩個有限集的無交併的勢(參看 [4])。
有了加法的初步概念,對於較大的數如 58,就可以用分為 10 個一堆的 5 堆及 8 個的1堆。這樣也初步認識了十進制。
在這個階段還可以學習比較多少,這也是對於順序的更深刻理解。
一般説來,對於數字符號的認識也在這一步。
第三步:一百以上的數的認識
在這一步,學習十進制是必不可少的,而為此需要認識數字符號。
加法和大小比較都需要深入,而且需要由大小比較引導到減法。學習加法和減法都需要學豎式筆算。另外還要學習使用計算工具。早年使用的算盤,對於理解十進制和加減法都很有效,現在即使不用,也需要有替代的教具。僅學會用計算器是不夠的。
在這一步,理解數的物理意義,越來越多地依靠應用題。
乘法也是在這個階段引進,有了乘法,就容易理解較大的數。學習乘法更要學豎式筆算,而且要背九九表。
關於背九九表,近年來有很多爭議,例如説美國小學生是不背九九表的,還有用計算器也不需要背九九表。但背九九表可以對於數和乘法有更好的認識,有利於駕馭計算器等工具。
另一方面,只有在充分理解數和乘法的條件下,背九九表才有數學教育意義。有的家長在孩子很小尚未理解數的物理意義時,就讓孩子背九九表(為了參加比賽或者顯示聰明),其實和背“人之初性本善”一樣,只會背而不解其意。這樣的教育很可能傷害孩子學習數學的前途(參看 [3])。
第四步:認識整個自然數
只有認識了整個自然數集,才能説是認識自然數了。
華羅庚先生曾經這樣生動地描述小孩子識數的過程(見 [2]):
“小孩子識數,先學會數 1 個,2 個,3 個;過些時候,能夠數到 10 了;又過些時候,會數到20,30,…,100 了,但後來,卻決不是這樣一段一段地增長,而是飛躍前進。到了某一個時候,他領悟了,他會説:‘我什麼數都會數了。’這一飛躍,竟從有限躍到了無窮!”
只有經過了這個飛躍,才真正能説是識數了。
但這個“大徹大悟”的過程,是隻能由孩子自己完成的。對於這個過程,華羅庚先生解釋説:
怎樣會的?首先,他知道從頭數;其次,它知道一個一個按次序地數,而且不愁數了一個以後,下一個不會數。也就是他領悟了下一個數的表達方式,可以由上一個數來決定,於是,他也就會數任何一個數了。
教育者則只能引導,如上面所説,講了一百以內的數再講一千以內的數、一萬以內的數、一億以內的數,等等,逐步擴展孩子的知識和想象力,直到孩子完成這個“飛躍”。在完成之前,教育者需要有足夠的耐心。
華羅庚先生所説的“從頭數”、“一個一個按次序地數”、“不愁數了一個以後下一個不會數”,在數學中可以嚴謹地表達為“皮亞諾公理”。一個好的數學教育者應該明白,自然數集就是滿足皮亞諾公理的集合(參看 [4]),而且應該理解自然數集的無限性,這是人對於無窮的第一個科學認識。
第五步:對自然數的認識的加深
自然數是非常深奧的,即使數學家也還有很多不明白之處(準確地説,我們不知道的遠比知道的多)。僅僅會數數,即使對於小學生認識自然數也是很不夠的。因此,在上述識數的過程中和識數以後,還要有更深入的學習。
具體説,至少要學習這幾個方面:
1) 帶餘除法,這方面可參看[10]。2) 質數(即素數)及質因數分解,這是數論的初步概念,學生由此可以看到自然數的複雜性和研究的難點。3) 數的擴展,包括分數、小數等。
今天仍是在中學數學中才講到的負數,其實有可能下放到小學。這方面的內容並不難,以往不能在小學講主要是因為心理上難以接受(在古代甚至很多數學家也拒絕接受負數),但今天負數在生活中已很常見,如温度、海拔、科學記數法(負指數)、記賬將支出記為負的收入、比賽將失分記為負的得分,等等。因此心理障礙應該小多了。
可能有人會問:既然數的範圍擴展了,為什麼還説自然數最重要呢?分數或有理數的範圍更大難道不更重要嗎?
這裏有個哲理性的問題:更大的範圍是否就更重要?自然數能夠擴充為有理數,是由其內在的因素決定的(沒有自然數的內在原因,即使人工地構造出負數和分數也不能滿足運算法則,參看 [4])。通俗地説,分數的性質都能由自然數的性質導出,但反之不然,例如對於一個整係數方程,即使能給出有理數解也未必能由此判定是否有整數解。在數論中對此的觀點是“局部與整體的關係”,即有理數是對於整數的“局部化”,整體決定局部但局部未必能決定整體。
4) 數的運算法則和大小關係(包括分數的大小比較)。
這幾個方面各有難點,仍需要教育者的耐心。此外,需要應用題更多而且更深。
由上述幾個必由步驟,足以看到學習自然數是相當不簡單而且漫長的過程,而且經常需要教育者幫助孩子克服難點。一個常見的問題是很多家長對此頗不耐煩。
4 小學數學素質的達標要求
小平邦彥認為,在小學通過數的計算的反覆練習來培養學生數學的基本學力是最基本的(參看 [1])。筆者認為這很有道理。
為什麼要反覆練習呢?因為孩子一開始總要出錯,只有反覆練習才能使錯誤逐漸減少。
那麼少犯錯甚至不犯錯就是終極目標嗎?不然的。孩子不是學習機。在反覆的犯錯-糾錯過程中,孩子會逐漸悟到一些深刻的道理,這對於孩子成才非常重要。
一是明白數學(首先是自然數)的絕對真理性。在犯了很多錯被糾正的過程中,孩子逐漸認識到,像 2+3=6 這樣的錯誤,永遠是自己的錯而不是數學的錯。由此建立對於數學的信念。
二是對於科學(首先是數學)的敬畏之心。犯了錯誤要勇於承認和改正,而不是狡辯。無論自己多聰明,也不應該對數學耍“小聰明”,例如用詭辯否認 1+1=2。如果和數學對抗,更是必死無疑。
三是逐步樹立嚴謹的科學態度。一絲不苟,精益求精,是科學技術工作所必須具備的基本素質。這種素質必須從小培養,否則將來就成了廢人。而自然數的學習是培養嚴謹科學態度的一個基本途徑。
那麼,怎樣才叫小學數學素質達標了呢?
如前面所説,除了自然數外還有很多其他知識要學,當然這些都是達標所必需的。但最核心的一點,是上面所説的“可靠性”。最低限度,如果自己的錯誤被別人指出,能夠立刻明白並自行改正。如果自己也能發現和確認別人的錯誤,那水平就高了一個檔次。最高的是能嚴格審視自己的工作,找出所有的錯誤並改正,從而保證自己的工作有高度的可靠性。這樣的孩子才是將來社會特別需要也特別有發展前途的。
這裏似乎與很多人的觀點相悖:社會發展靠創新呀!沒錯,但創新需要先打好基礎。對於小學生,首先需要學會把最基本的事情做對做好。沒打好基礎就“創新”,是“先天不足”。前面所説的“探索性學習”、“項目式學習”等,並非沒有道理,但在沒有打好基礎之前就搞這類創新性的學習,例如讓孩子自己“探索勾股定理”,就如大躍進“放衞星”,其實都是造假忽悠,結果將是害了孩子。
能夠創新的小學生不是沒有,但是極少。不應把適合極少數孩子的教育方法用於大多數孩子。
5 超越自然數
現在來討論前面所説的“中學數學下放到小學”。如前面所説,這並非對所有小學生都合適。但是小學數學如何與中學數學銜接,是一個對於一般的小學教育都值得研究的課題。
早年中學生的第一個數學困難是“用字母表示數”,那時很多中學生剛開始學甚至還沒學英語,這方面的困難是文科性的。現在很多孩子小學就學英語,文科的困難小多了。但數學上的困難依舊,就是説對於用字母表達的數學的理解是一個坎。
我們來具體分析一下初中生首先接觸的用字母表達的數學。最基本的有兩個方面:恆等式與方程。恆等式如a+b=b+a;方程如 3x+4=10。由於它們都還可以用“數”來解釋,很多人沒有理解它們都已超出了“數”的範圍。前者可以用語言敍述為“兩個數相加,交換加數的次序,和不變”;後者可以用語言敍述為“有一個數,它的 3 倍加 4 等於 10”。然而在邏輯上,它們都比數的運算升了一級。
具體説,恆等式a+b=b+a 的完整敍述是“對任意兩個數a,b都有a+b=b+a”;而方程 3x+4=10 的完整敍述是“有一個數 x 使得 3x+4=10”。這裏關鍵是有了謂詞“任意”(即“一切”) 或“有”(即“存在”)。我們知道謂詞演算是比命題演算高一級的邏輯運算。
不理解謂詞,實際上並沒有真正明白恆等式與方程。這是初中代數的理解困難的基本原因。
但對於進一步學習數學,這一步是必須邁出的。初中平面幾何中的命題經常都有兩個謂詞,如“過兩點有一條直線”,完整的敍述是*“對平面中的任意兩個點A,B,存在一條直線 ℓ使得 A,B 都在ℓ**上”。*在微積分中的命題經常有三個謂詞,如數列極限
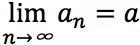
的完整敍述是“對任意正實數ε,存在一個正整數N,使得對任意整數 n>N有
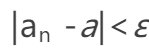
”。在更深是數學如實變函數論或概率論中,還可以看到有四個甚至五個謂詞的命題。由此可見,如果連只含一個謂詞的語句都不理解,是無法學習更深的數學的。
為了讓孩子們邁過這個坎,仍需要教育者有足夠的耐心。
上面所説的從小學數學到中學數學的過渡,需要在小學時期就做準備,主要就是對於恆等式和方程的準備。由上所述可見,這實際上已經超越了學習自然數的範圍。
在這方面有很多教學經驗值得分析和總結。下面講一些具體方法。
對於簡單的恆等式,可以先不用字母表述。例如上面的加法交換律,如果學生完全明白了,再理解 a+b=b+a就只是從文字表述到用公式表述的轉換。
對於方程,則可以先多做應用題,例如買一樣東西已知單價 3 元付了 10 元找回 4 元,問買了幾件。
小學裏的應用題有些較複雜也較難,而且有一些常見題型,如行程問題、工程問題等。很多應用題可以轉化為方程。這裏舉人們經常討論且爭議頗多的“雞兔同籠”為例。
雞兔同籠原本是我國古代用於鍛鍊學生解題能力的問題,例如“今有雉兔同籠,上有三十五頭,下有九十四足,問雉兔各幾何?”這裏不言而喻每隻雞有兩條腿而每隻兔有四條腿。
歷史上(甚至直到今天)這個習題一直不斷地受到攻擊、貶低和挖苦,罪名如“牽強附會”,“理論脱離實際”,“為什麼要把雞和兔子關在同一個籠子裏”等等。在文化大革命中甚至被説成是反革命的(參看例如電影《向陽院的故事》)。其實農民把雞和兔裝到同一個籠子中拿到市場上去賣,是很平常的事(見照片)。

雞兔同籠題對於一般的小學生是很難的,能自己做出的孩子都很聰明。如對於上面的題目,有的孩子説:“如果把雞的翅膀也當作腿,那麼無論雞兔都有 4 條腿,總共就會有 4×35=140 條腿,但題設只有 94 條腿,那麼多出來的140-94=46 條腿應該都是翅膀,這樣就知道共有 46÷2=23 只雞,從而兔有 35-23=12 只。”
那麼大多數孩子做不出來又怎樣呢?無非是下列幾種情形:有的孩子做不出但很想知道答案,就從別的途徑尋求答案;有的孩子做不出就放棄了,甚至以後就忘了;有的孩子由此覺得數學很有奧妙,雖做不出但提高了對於數學的興趣。無論哪種情形都不是壞事。
那麼,教育者是否需要給不會做的孩子講做法呢?這是愚蠢的,因為此題的一般解法對於數學教育並無意義。
即使在中國古代的數學著作(如《九章算術》)中也有很多可以轉化為方程的問題。例如對上面的雞兔同籠題,設雞有 x只,兔有y只,則題設可以用方程表達為
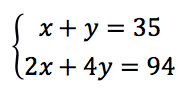
有人會説這太繁了,可以用一元方程表達。其實不然,列一元方程需要數學推導,而上面的方程組只是按原題轉述而已。
在學生學了方程之後,這類問題都將成為很容易而且不需要很聰明就能做的題目。因此,過多地講“題型”是沒必要的。
那麼不能先講方程再用來做這類應用題嗎?其實現在有些人就是這樣主張的。有了一般方法就可以應用於解決很多特殊問題,這樣效率不就高了嗎?類似的主張在中學數學教育中更多。
小平邦彥對此堅決反對,認為“數學教育應按數學發展史順序進行,而不是按邏輯基礎來進行”(參看 [1])。筆者很贊同他的觀點。
在邏輯上,固然是由一般可以推導出特殊,因此掌握了一般原理就可以用於解決很多具體問題。但**人的學習規律,是從特殊到一般,從具體到抽象,從簡單到複雜,從容易到難,從低到高。不掌握足夠的特例,是不能深刻理解一般規律的。**在這方面教育不能偷工減料,老師省事了學生就苦了。
最後強調一點:由上所述可見,自然數的教學對於小學數學教師的要求很高。好的數學教師應該對於自然數有深刻的認識,並儘可能廣泛地瞭解自然數的物理意義。
參考文獻
[1] 代欽:小平邦彥的數學教育思想------兼論數學家與數學教育家的爭論. 《數學通報》2007 年第 6 期
[2] 華羅庚:《數學歸納法》,《數學小叢書》 15,科學出版社(2002)
[3] 姜樹生:可怕的幼兒數學教育(2011.3.)
[4] 李克正:自然數的定義和基本性質(2017.11.)
[5] 李克正:怎樣學好數學,返樸網(2019.9.)
[6] 李克正:現代社會對於勞動者的數學素質的需求(2019.11.)
[7] 蓮溪:是誰奪走了美國人的數學能力?--美國百年數學戰爭演義,皮皮蝦網(2017.3.)
[8] 其故:得數學者得天下,返樸網(2019.8.)
[9] 鹹道:致家長(2018.4.)
[10] 鹹道:帶餘除法的重要性 ------ 續“致家長”(2019.1.)
[11] 小學數學新課程標準(2011年版)
[12] 尹裕:數學啓蒙教育之我見(2014.2.)
[13] 朱忠明:中學生數學素養測評模型的構建與實測研究(2018.3.)