讀科技史 ，啓迪智慧人生（二）--錯綜複雜的數學及哲學源流_風聞

前言

  科學技術是第一生產力，科技史是人類第一史。英國科學史家丹皮爾曾説：“再沒有什麼故事能比科學思想發展的故事更有魅力了”。本文檔 以 推動科技史 關鍵 人物為線索，參考史記的方法，將人類 （西方） 科技史串聯起來，提供了 科技史中 每 個 關鍵 人物 所在年代與中國朝代對應關係。

   讀史使人明智 ；讀科技史 ，啓迪智慧人生。

   本文的編輯與發佈，其目的是推廣科學技術的思想與智慧，提高人們（ 尤其是青少年朋友 ）的科 學素養，把大家從娛樂至死、沉迷遊戲 的社會現實中解救出來，帶領大家一起學習科學家的偉大精神，形成尊崇科學，學習科學，探索未知的精神。閲讀本文檔中的每一個科學家故事 ，最好擁有高中以上 知識水平。

    前文介紹了西方的血火歷史背景，本篇開始切入科技史敍事，先介紹錯綜複雜的數學及哲學源流。

二、錯綜複雜的數學及哲學源流

不瞭解數學史，就不可能全面瞭解數學科學，也不可能全面瞭解整個人類科技史、文明史，本篇以數學大事記為主線，穿插歷史背景圖片，以啓發讀者思考。

世界數學史

古文明時期：10 進制（巴比倫 60 進制，瑪雅 20 進制），結繩計數、刻痕計數；尼羅河氾濫、天文觀測產生幾何學；

   1、埃及萊茵德和莫斯科紙草書：無位值概念，單位分數 1/n，PI=3.16，討論線性方程；巴比倫泥板文書：60 進制，位值概念，開方根 1.414，三項二次方程，三次方程（查表），PI=3（3 又 1/8），普林頓 322 泥板文書（公元前 1600年）4 列 15 行表格記錄了勾股數組。

   2、公元前 6 世紀，畢達格拉斯是古希臘的哲學家和數學家（約前 582-500 年），傳説發現了勾股定理，並宰了一百多頭牲畜來祭祀繆（miu）斯女神。現在普遍認為在畢達格拉斯之前，已為巴比倫人所知。其實中國西周數學家商高已提出了勾股定理，比畢達格拉斯早 600 多年。畢達哥拉斯學派相信任何量都可以表示成兩個整數之比，萬物皆依賴於整數。但正方形的對角線和一邊比是不可公度的（無理數 1.414…）。有一次他們航行在海上開會，一個學員發現後，學派驚恐不已，把這個學員拋進了大海。根號 2 等無理數的發現引起了第一次數學危機。

    3、公元前 5 世紀，安提豐提出圓內接正多邊形逼近圓面積來化圓為方（古希臘三大幾何問題：化圓為方；倍立方體；三等分角（限尺規作圖），成窮竭法的始祖。

    4、公元前 4 世紀，亞里士多德《物理學》記載了有關無限性概念的 4 個悖論：兩分法運動不存在；阿基里斯追不上烏龜；飛箭靜止；運動場空間和時間不能由不可分割單元組成。亞里士多德研究數學推理的出發點的基本原理，區分為公理和公設（一切科學的真理和某門科學第一性原理），創立邏輯學矛盾律（一個命題不能同時是真的又是假的）和排中律（一個命題或者是真的或者是假的，二者必居其一），使數學推理規律規範化和系統化，為歐幾里得演繹幾何體系奠定了方法論的基礎。

   5、公元前 4~3 世紀，歐幾里得《幾何原本》：5 條公里，5 條公設，119 個定義，465 條命題，歷史上第一個數學公理體系。

   6、公元前 3 世紀，阿基米德窮竭法求面的周長和麪積；平衡法求球的體積；體現了近代極限與微積分的思想。平衡法發現；窮竭法證明。

   7、公元前 3~2 世紀，阿波羅尼奧斯《圓錐曲線論》，從一個對頂錐得到並命名橢圓（ellipse）、雙曲線（hyperbola）和拋物線（parabola），在對它們性質的研究中已經包含了近代微分幾何和射影幾何的課題。

   8、公元 2 世紀，托勒密《天文學大成》總結了古代三角學，並制定了弦表（正弦函數表）公元 3~4 世紀，丟番圖《算術》中對不定方程求解，因此不定方程又叫丟番圖方程。z^2=x^2+y^2。引出了後來的費馬大定理（n 大於 2 時，沒有正整數解，1994 年被英國數學家維爾斯最終解決），創用了一套縮寫符號並用特殊符號表示未知數代替之前的文字敍述，是代數符號的起源公元 2~3 世紀，巴基斯坦巴克沙利村莊樺樹皮上的手稿出現完整的十進制數碼，零用點表示，後來（至遲不超過 9世紀）逐漸演變為圓圈。零是偉大的發明，簡化了加減乘除運算。公元 8 世紀印度數字傳入阿拉伯，然後傳入歐洲，零稍晚傳入，至遲在 13 世紀斐波那契《算經》已經有包括零在內的完整印度數字介紹，對歐洲近代科學進步扮演重要角色。

    9、公元 8~9 世紀，阿拉伯花拉子米《還原與對消計算概要》在 12 世紀翻譯成拉丁文，在歐洲產生巨大影響。阿拉伯語 al-jabr 以為還原和移項，成為當今英語 algebra 的來源，因此也叫《代數學》，敍述一、二次方程求解問題。另一本《印度計算法》，系統介紹了印度數碼和十進制記數，使印度數碼在阿拉伯流行起來，並隨後被翻譯成拉丁文傳播到歐洲，讓歐洲誤以為是阿拉伯數字。

   10、5-11 世紀，天主教成為歐洲絕對勢力，歐洲黑暗時期。12 世紀，開始大量翻譯阿拉伯文、希臘數學書籍為拉丁文。

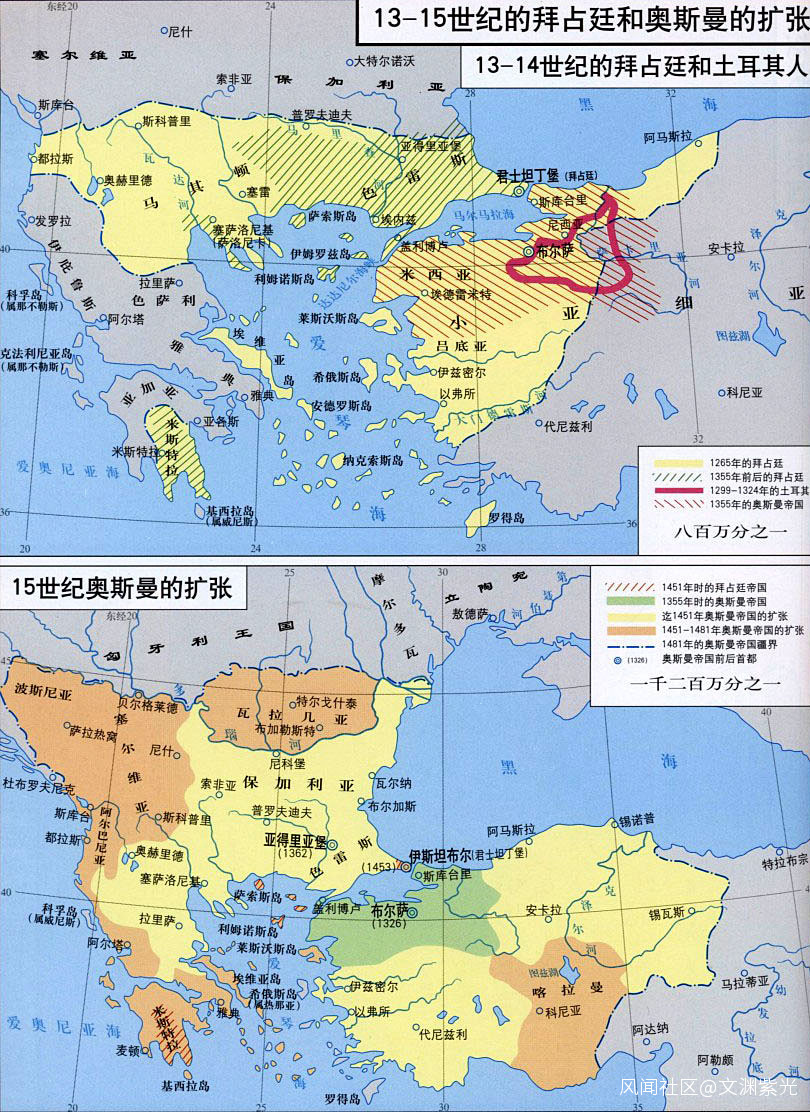
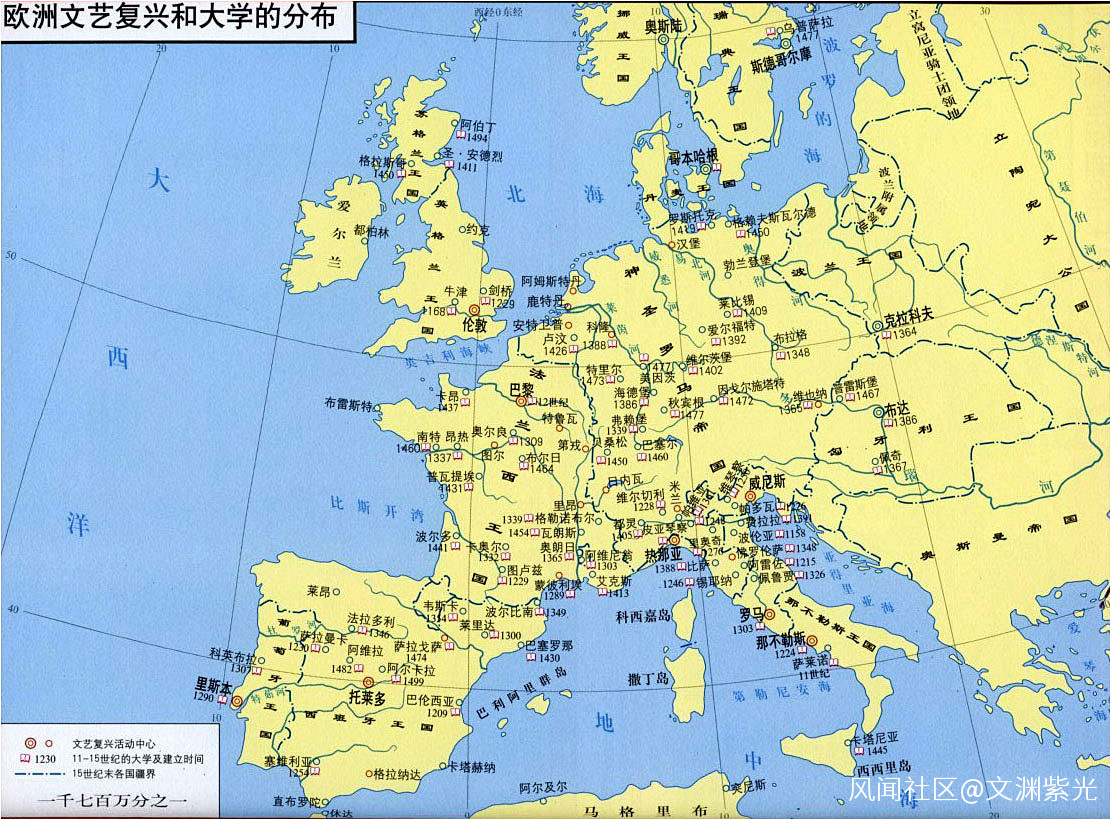
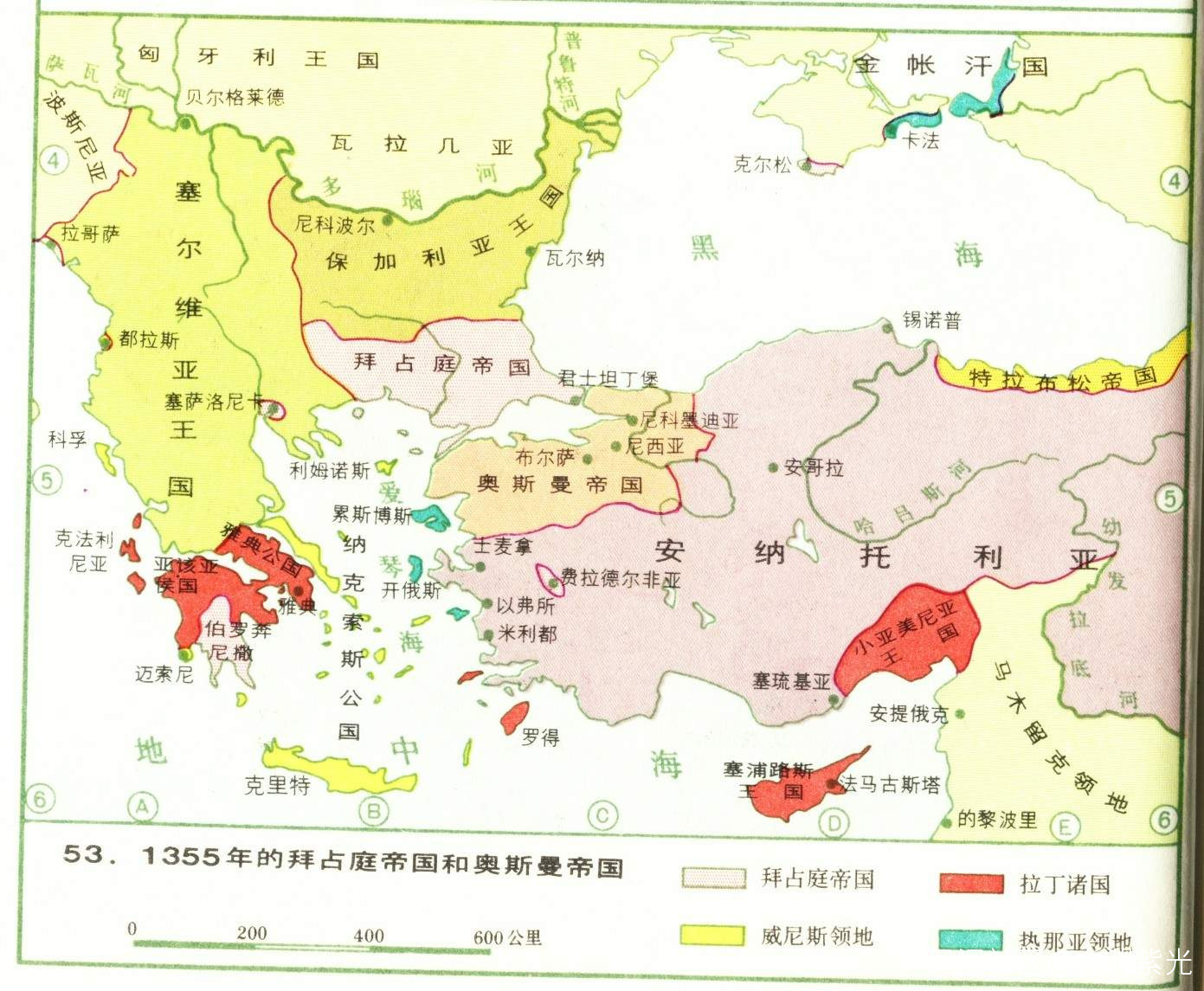
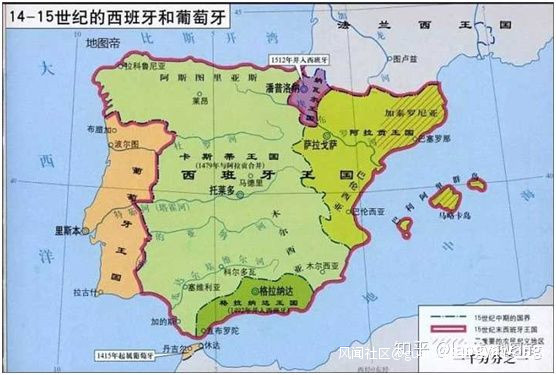
    11、13 世紀，意大利斐波那契寫成《算經》彙集中國，印度，希臘數學問題彙集，系統介紹了阿拉伯印度數字，修訂版記載了“兔子問題”並導致了著名的斐波那契數列。

    12、15 世紀，意大利費羅和塔塔利亞挑戰解 3 次方程，後者獲勝並把方法秘密傳給了卡爾丹。卡爾丹違背承諾在《大法》中公開了這些解法，推廣到了一般情形並給出了幾何證明。其學生費拉里解決了 4 次方程。《大法》對不可約情況感到困惑（其實已經邂逅了複數）。邦貝利在教科書《代數》中引進了虛數，以解決三次方程不可約情況。卡爾丹已經認識到復根是成對出現並且三次方程有三個根，四次方程有四個根。荷蘭人吉拉德在 17 世紀的《代數新發現》裏進一步推斷 n 次方程 n 個根，即“代數基本定理”，但沒有證明。

​

    13、 16 世紀，韋達在《分析引論》裏第一次有意識的使用系統的代數字母和符號，輔音字母表示已知量，元音字母表示未知量。笛卡爾改進為拉丁字母前幾個 a、b、c、d 表示已知量，後幾個 x、y、z、w 表示未知量成為今天的習慣。

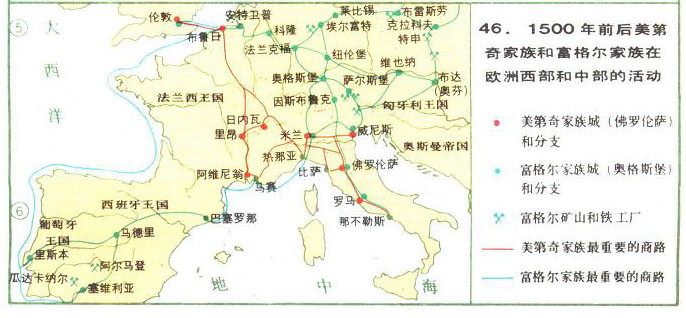
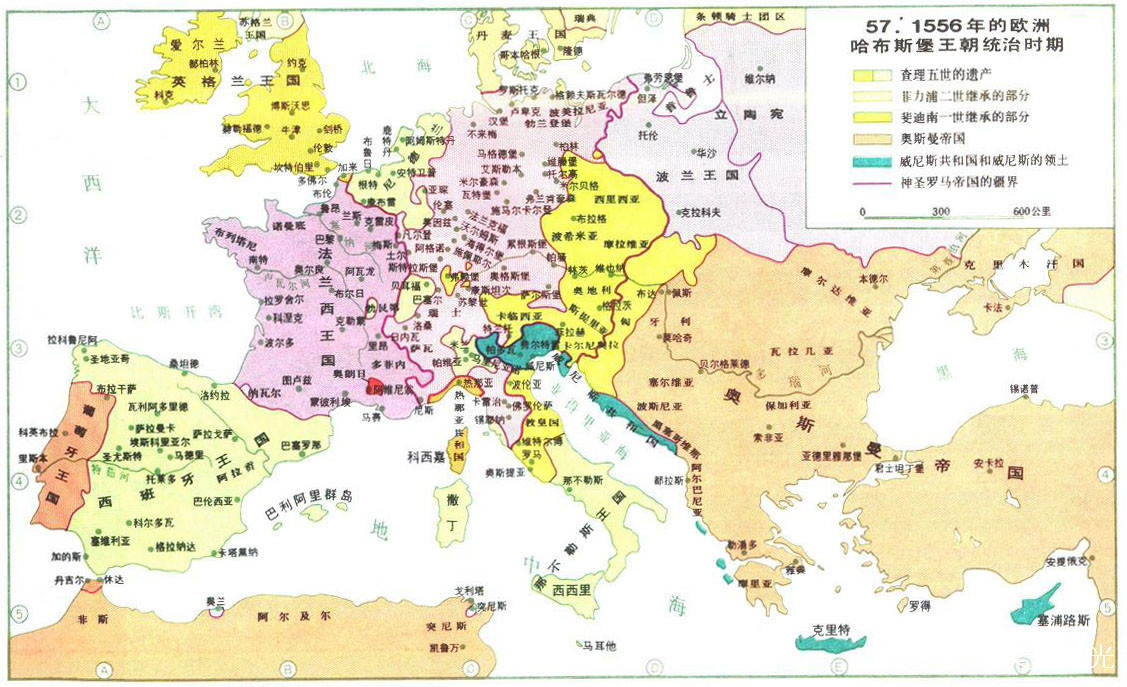
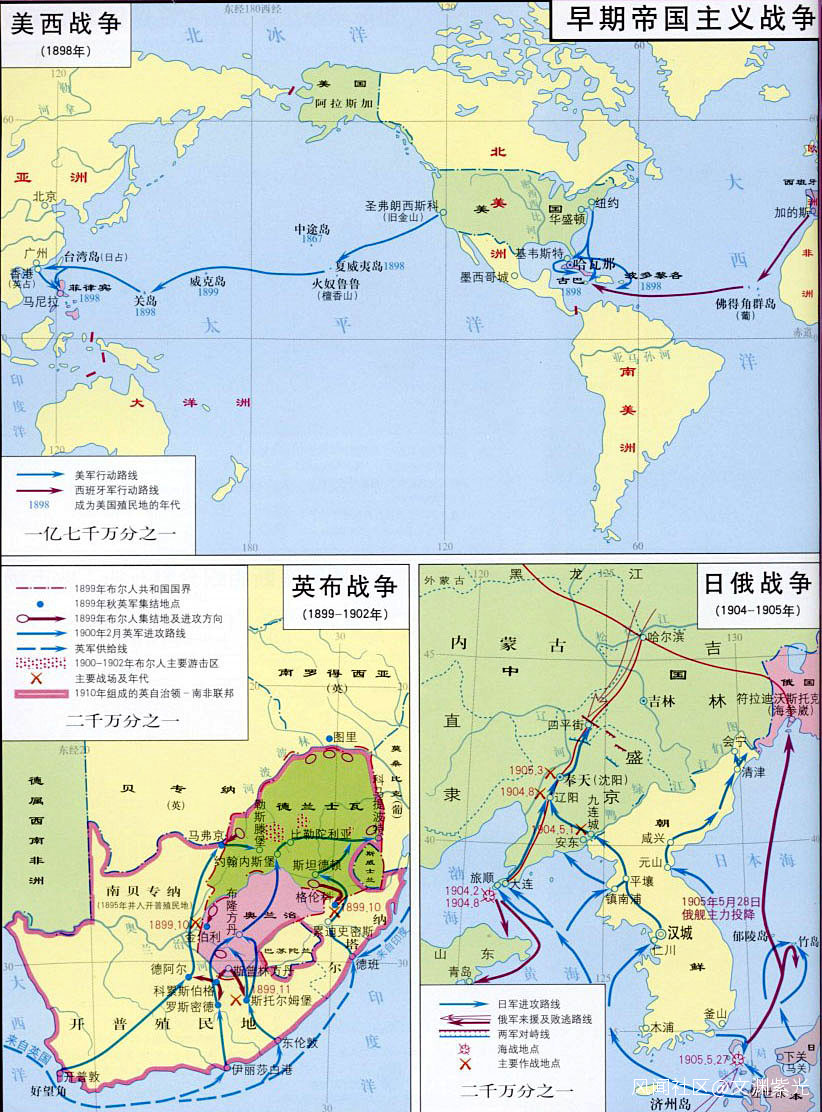
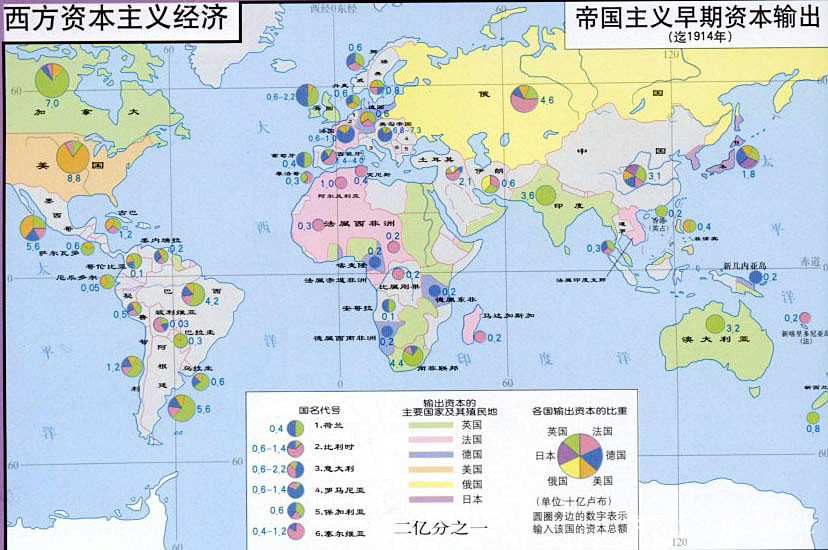
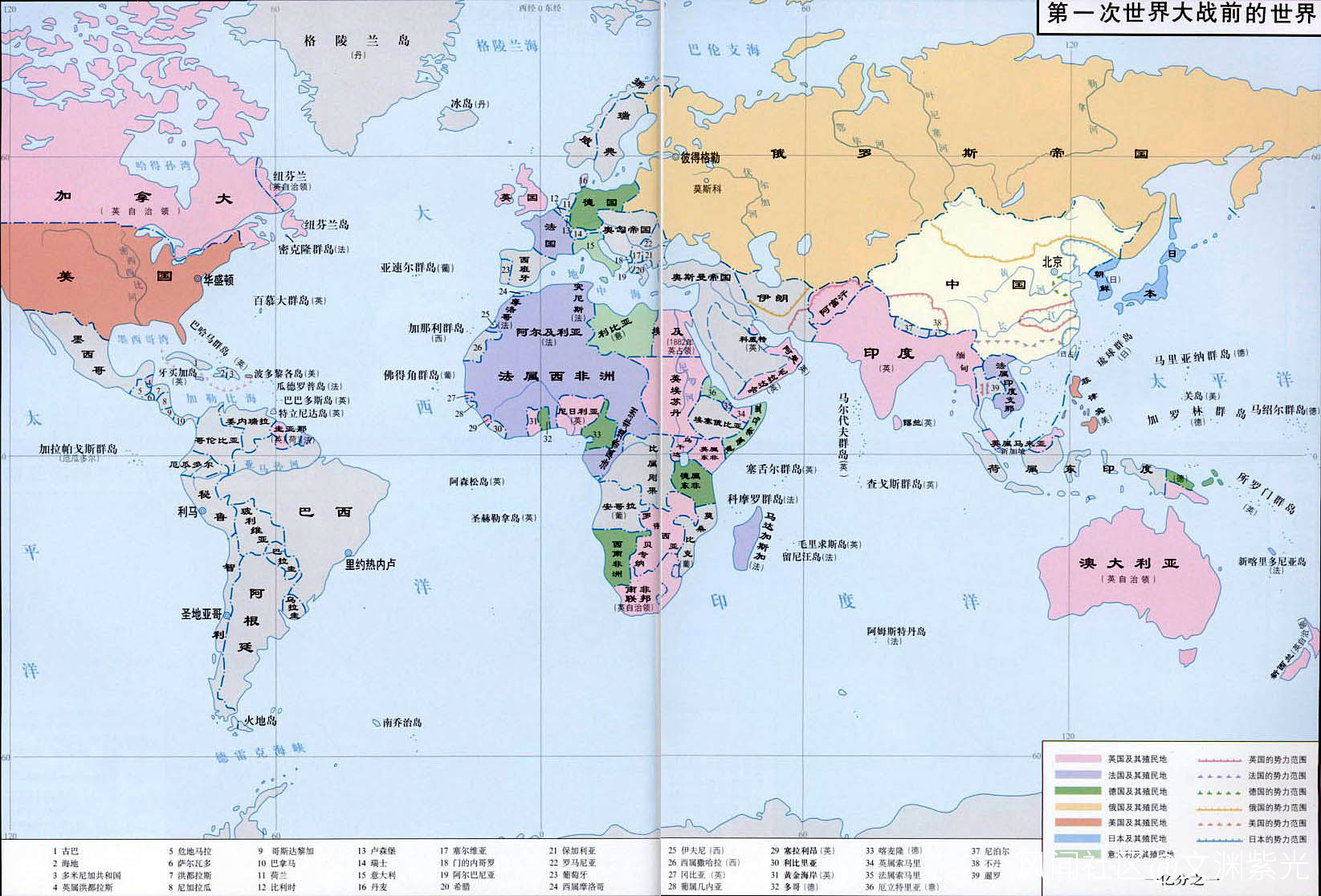
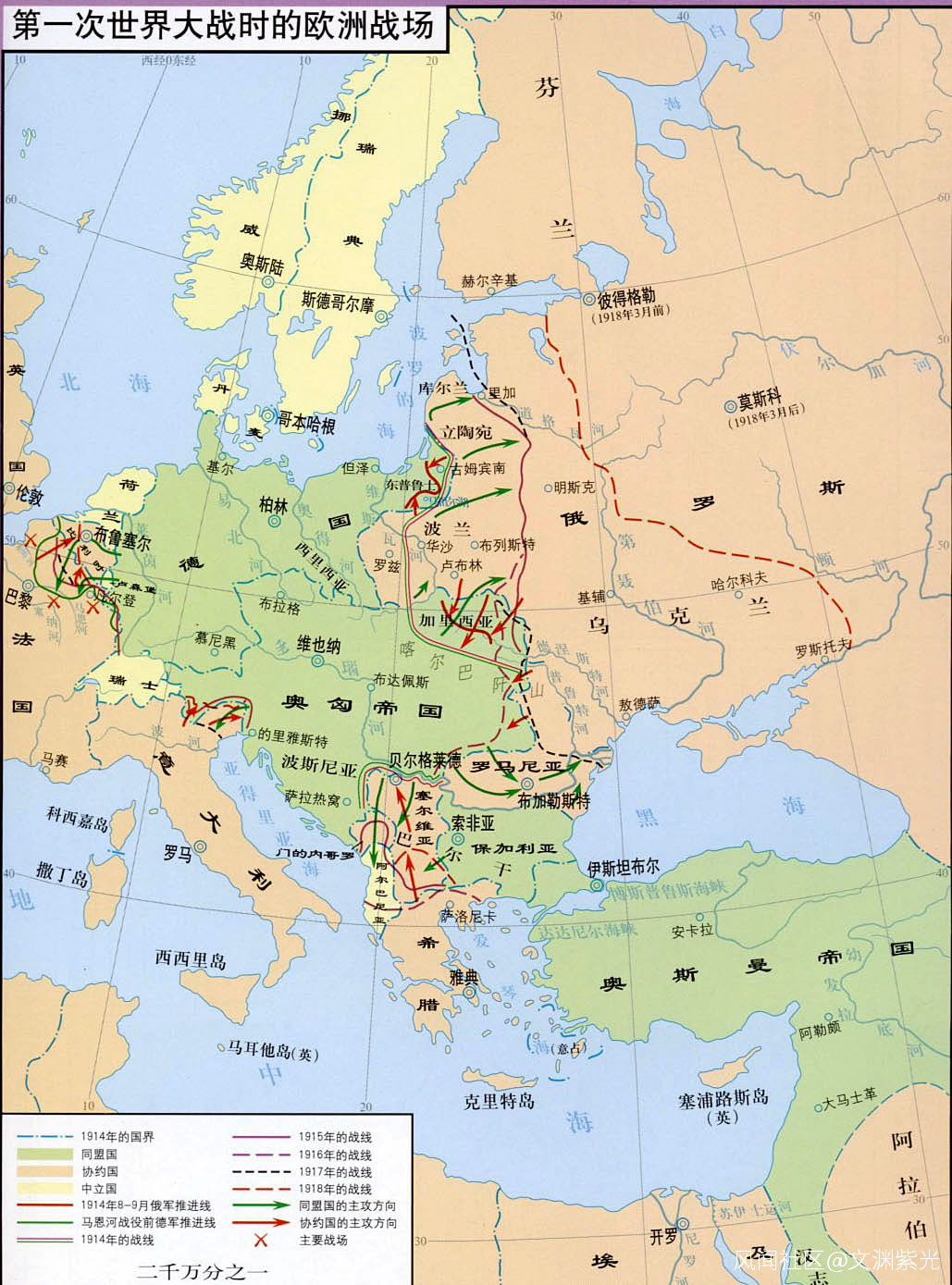
14、 利瑪竇及後繼西方傳教士在華的學術交流活動及 禮儀爭執

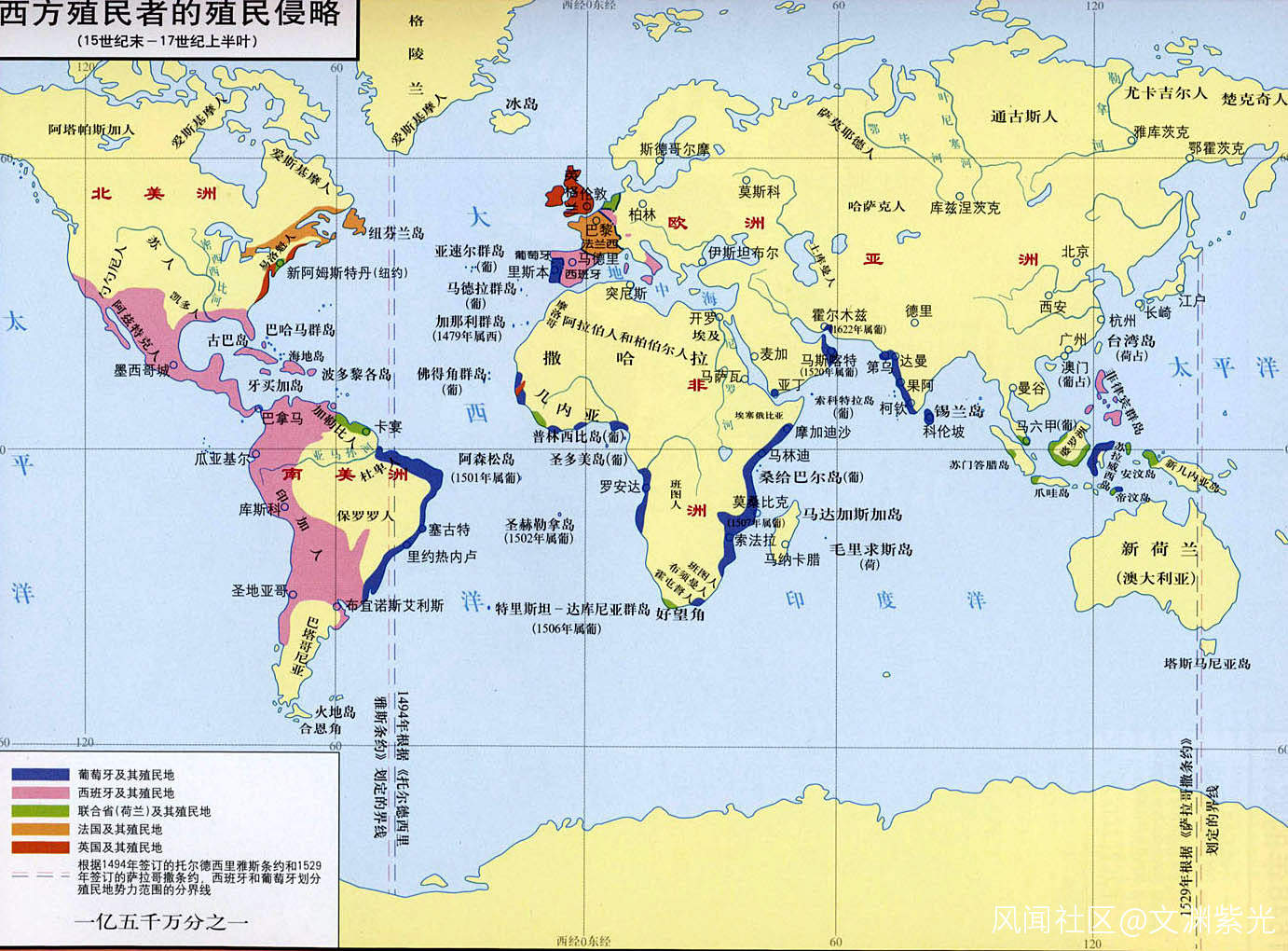
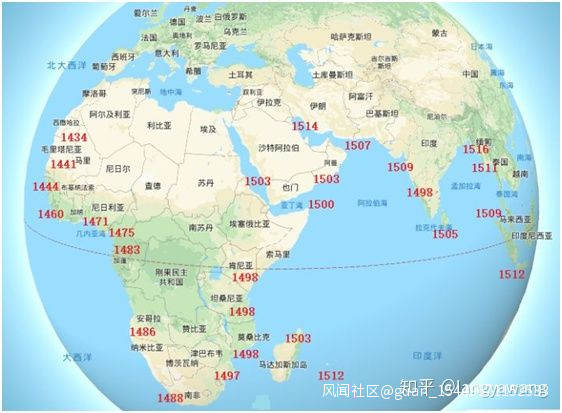
西方印度洋開拓順次圖

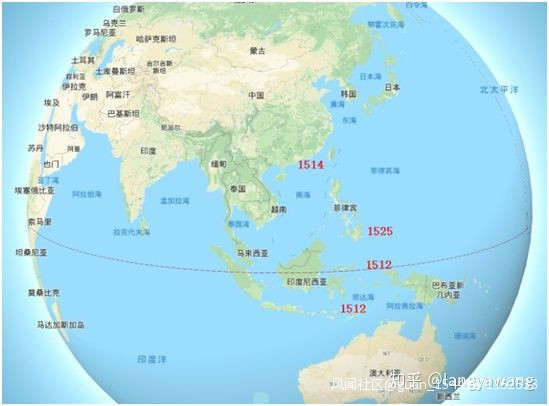
西方南洋開拓順次圖

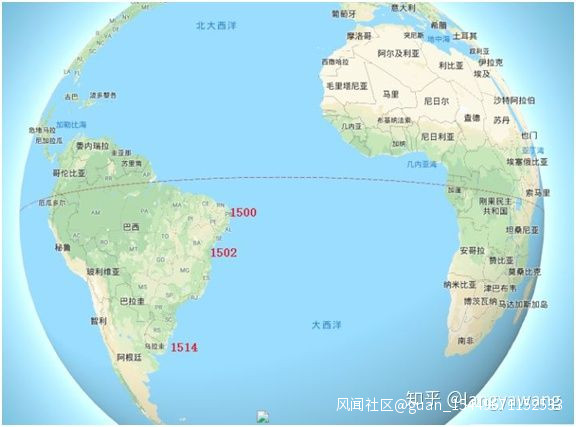
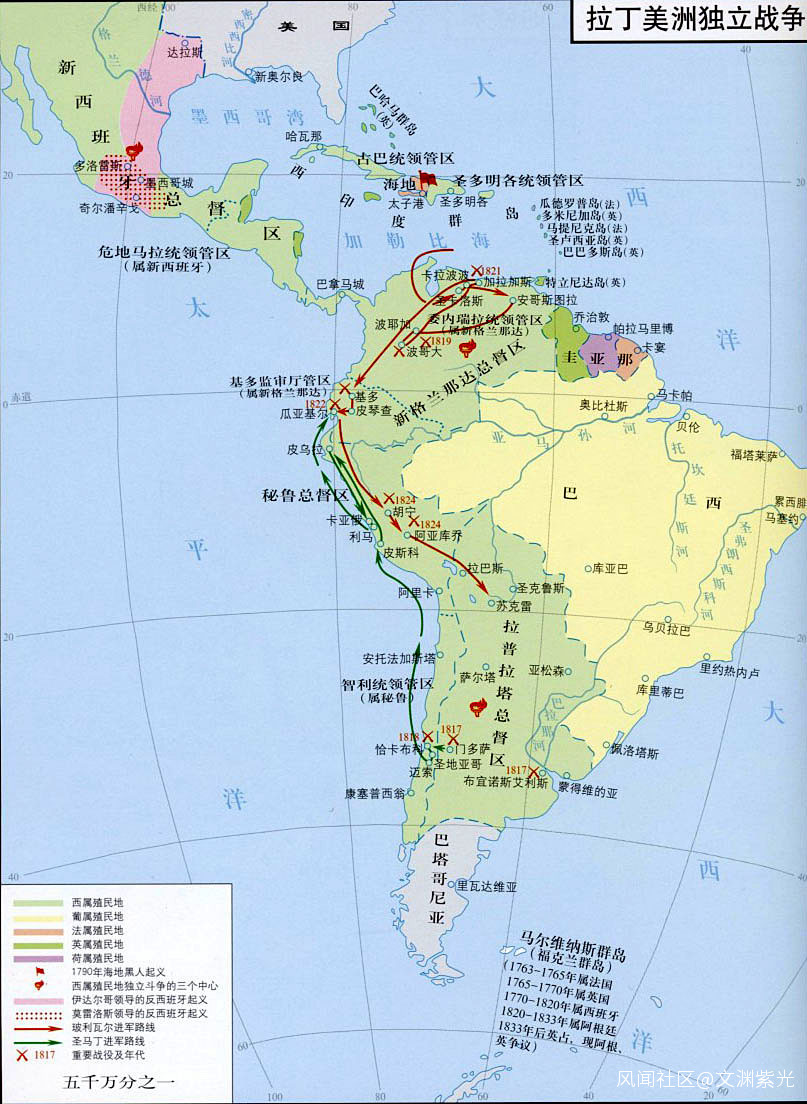
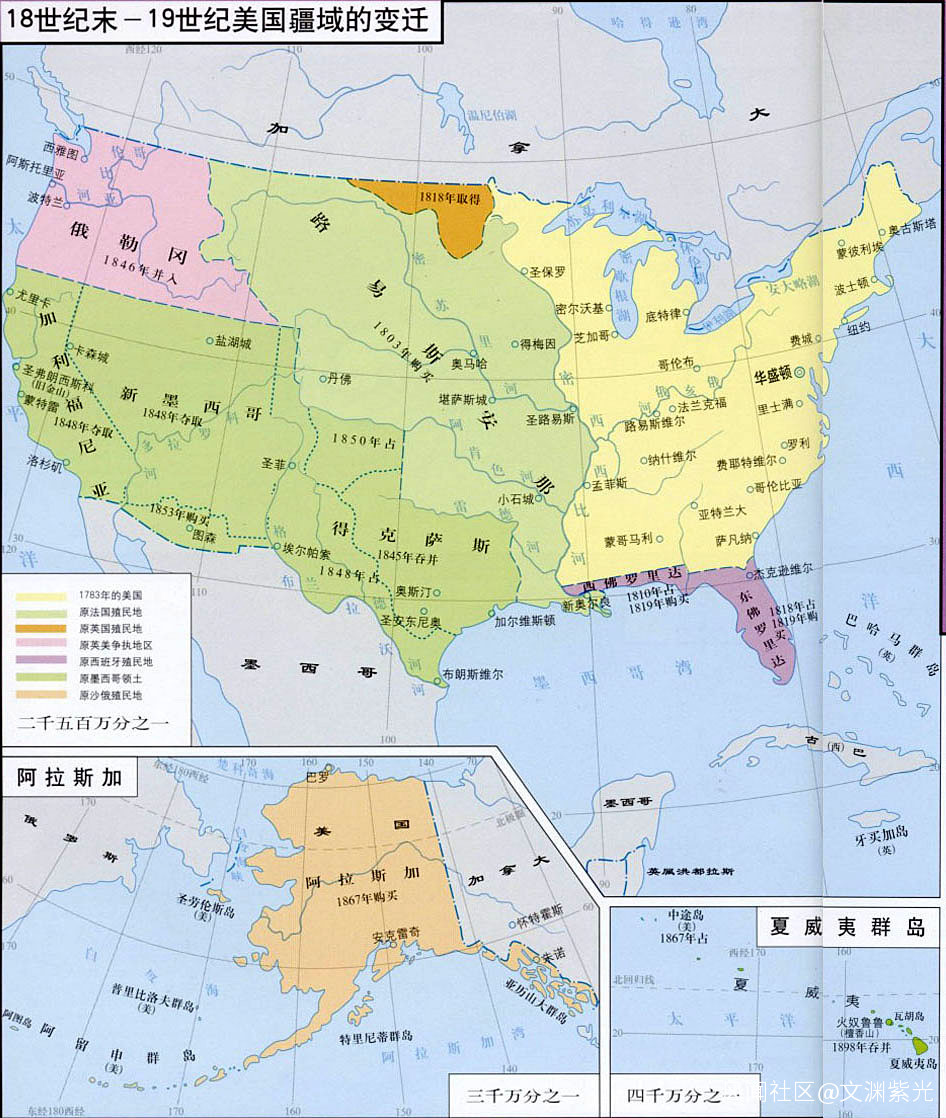
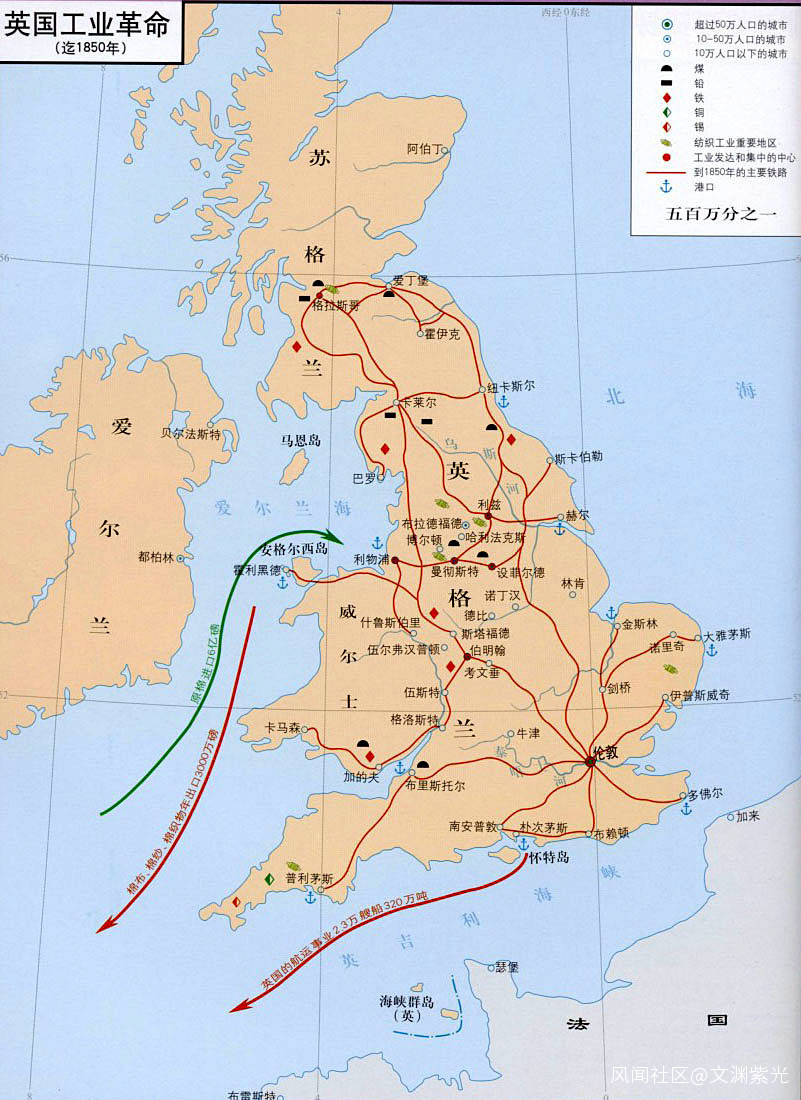
西方美洲開拓順次圖

          1582年（明朝萬曆十年），耶穌會意大利籍傳教士羅明堅及利瑪竇抵達廣東肇慶，為近代天主教入華揭開序幕。

          1601年（明朝萬曆二十九年），意大利耶穌會傳教士利瑪竇抵達燕京，一度自喻為“西僧”，但他旋即發現中國文化由儒家士大夫掌握。他相信要中國人接受天主教，必須從士大夫階層着手，他於是改稱為“西儒”，研習儒家文明，穿起士大夫服飾，向中國人介紹記憶術、地圖、天文等西方技術，以此表明他們並非文化低落的“西夷”。

         利瑪竇容許中國教徒繼續祭天、祭祖、祭孔的舊俗，利瑪竇主張中國人所謂的“天”和“上帝”本質上與天主教所説的“唯一真神”沒有分別，故祭天並無問題。而祭祀祖先與孔子，這些只屬緬懷先人與敬仰哲人的儀式，與信仰也沒有什麼干涉；只要不摻入祈求、崇拜等迷信成分，本質上並沒有違反天主教教義。利瑪竇的傳教策略和方式，一直為之後到中國傳教的耶穌會士所遵從，是為**“利瑪竇規矩”。**

        1610年，利瑪竇去世，死前指定意大利人龍華民接任教會中職務，龍華民成為引發“禮儀之爭”的第一人。他於1597年（明萬曆二十五年）進入中國，先在韶州傳教，1609年入北京，對利瑪竇的思想和傳教方法有不同看法，但利瑪竇死後才提出。當他接任中國耶穌會總會長後，主張廢除“天”、“上帝”、“天主”等詞，一律採用譯音，並指“天”是指蒼蒼之天，而“上帝”並不是代表造物主，主張應將“天主”依拉丁文音譯為“陡斯”；也有人主張只許用“天主”，而不能用“天”與“上帝”之稱。

      耶穌會教士雖然對兩派主張意見分歧，但為避免紛爭鬧大，耶穌會決定焚燬五十多篇反對利瑪竇的作品，統一該會立場。這次糾紛只成為會內事務，但到了1628年，在華傳教士在江蘇嘉定舉行會議，討論敬祖及Deus的譯名問題。與會者意見很不一致，最終認為敬孔祭祖問題應沿用“利瑪竇規矩”；對於譯名，則主張採用龍華民一派的音譯。

     直至道明會進入這場紛爭，禮儀之爭才正式升級。道明會在華傳教事業，起步較耶穌會略遲。當耶穌會教士在中國朝廷及士大夫階層享有聲望時，1631年1月2日或3日（明朝崇禎四年），道明會的高奇神甫才從菲律賓抵達中國福建北部的福安，正式開始對華傳教，接任的黎玉範神父向教廷報告，指責耶穌會寬容中國信徒祭祖、敬孔，終引起羅馬介入。

     當時耶穌會受葡萄牙國王保護，基地是葡萄牙佔據的澳門，道明會受西班牙國王保護，基地是西班牙佔據菲律賓馬尼拉。而葡西兩國在海上對抗，關係緊張。

     1644年（清朝順治元年）清兵入關時，天主教入華已62年，德意志籍傳教士湯若望協助編制曆法，獲清廷信任，天主教得以迅速發展。

     1645年9月12日（清朝順治二年），羅馬教廷經教皇英諾森十世批准，發佈通諭禁止天主教徒參加祭祖祀孔，但到了1651年，耶穌會教士衞匡國到羅馬向教皇申辯，1656年（清朝順治十三年）教皇亞歷山大七世決定準許耶穌會士照他們的理解參加祭孔等活動，只要不妨礙教徒的根本信仰。

     1664年，耶穌會住院共38所，耶穌會士來華人數累計82人，全國的教堂已經有156座，全國天主教徒達245000人之多 。

湯若望和南懷仁

     1665年，楊光先發表《闢繆論》，批評湯若望曆法不準，當時顧命大臣鰲拜不滿外國人蔘議朝政，於是支持楊光先，把湯若望收押獄中，天主教在華髮展直挫，史稱“曆獄”。

 康熙帝

往後，康熙帝執政，禁錮鰲拜，重新起用外國人。南懷仁利用西方發明貢獻清朝，建立天主教士的聲望，又與利類思和安文思共同上奏，為湯若望平反。1669年（康熙八年）9月5日，康熙頒旨：“惡人楊光先捏詞天主教系  邪教  ，已經議復禁止。今看得供奉天主教並無惡亂之處，相應將天主教仍令伊等照舊供奉。”康熙初年，成為傳教士在中國的蜜月期。

南懷仁畫像

      1689年（清朝康熙二十八年），清朝與俄羅斯帝國準備劃訂疆界，商議尼布楚條約，精於拉丁文的傳教士負責代表中方與俄國人溝通，這條條約最終以拉丁文簽訂。南懷仁等亦協助清廷鑄造火炮，平定三藩之亂。他們準確預測日食，使皇帝可以為相關祭奠做好準備；一些耶穌會傳教士則成為宮廷畫家。

      1692年（康熙三十一年），康熙下達一道容教令，標誌着傳教士的勢力攀上高峯：

康熙年間，新來中國的多明我會（Dominicans）及方濟會（Franciscans）教士反對明末以來耶穌會教士容許中國教徒祭天、敬孔、祀祖等禮俗，爆發禮儀之爭，因此1720年（康熙五十九年）清廷決定禁教（未嚴格執行），1723年（雍正元年）清世宗開始嚴格執行禁教，再加上日後傳教士介入世宗與兄弟爭奪皇位之事，還有擔心民眾信奉天主教後，國家命令無法貫徹，且會被西方天主教國家控制，因此清世宗下令除留京任職的傳教士外，其餘一律送往澳門，各地天主堂被拆毀，或改成公廨，屢下禁令，不許民間信仰。清高宗乾隆年間，取締尤烈，因此傳教活動幾乎消失，直到公元1842清宣宗時期（道光二十年）爆發鴉片戰爭後，簽訂中國首條不平等條約——《南京條約》才解除禁令。

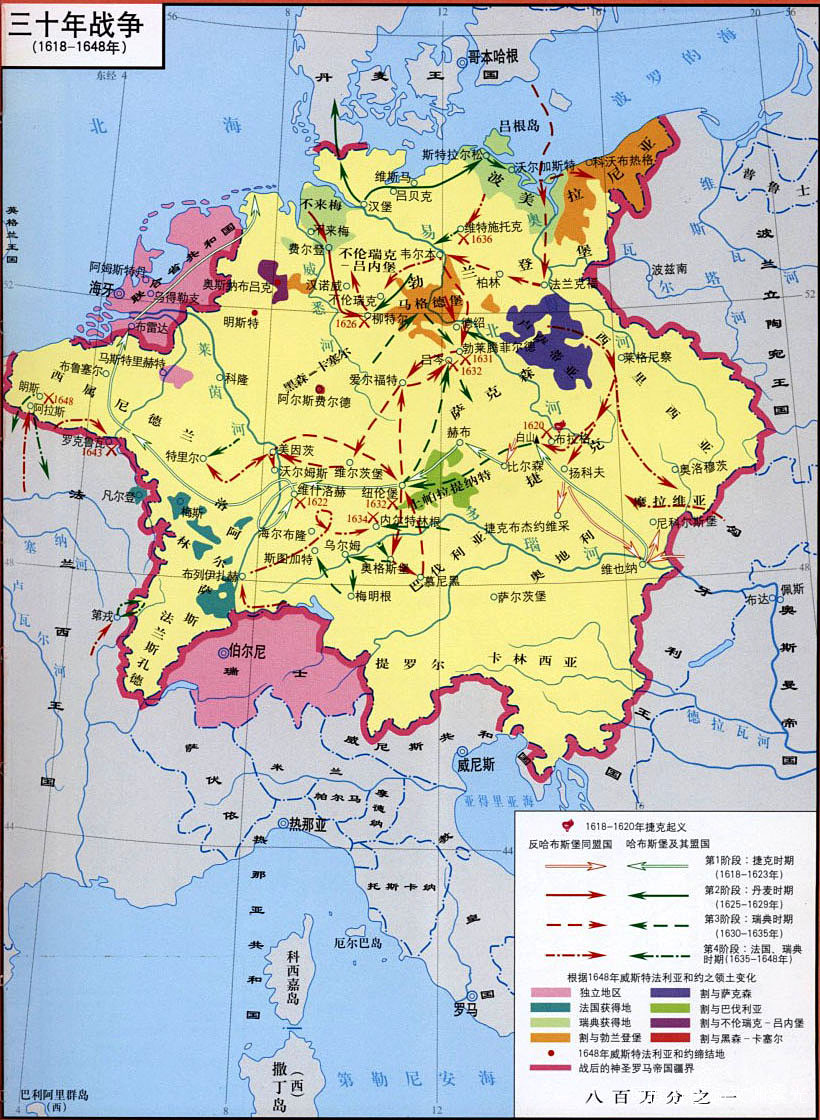
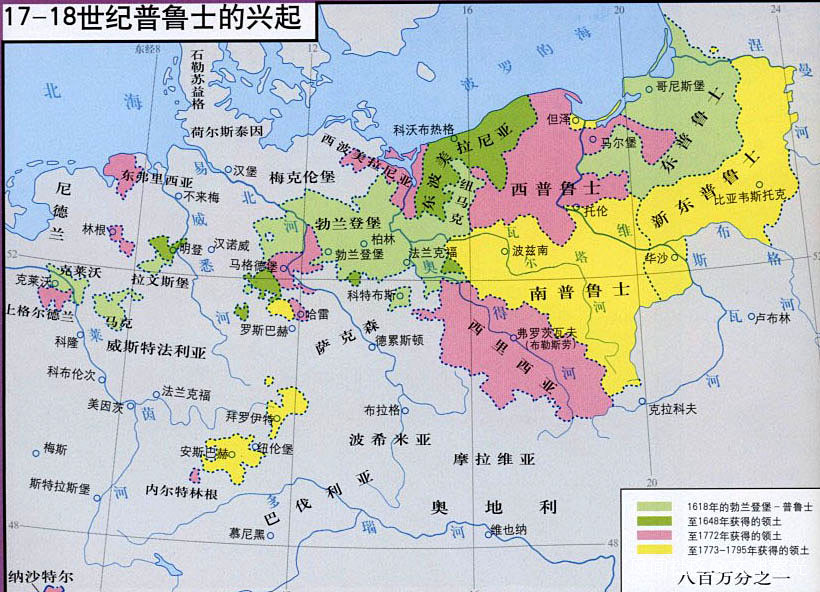
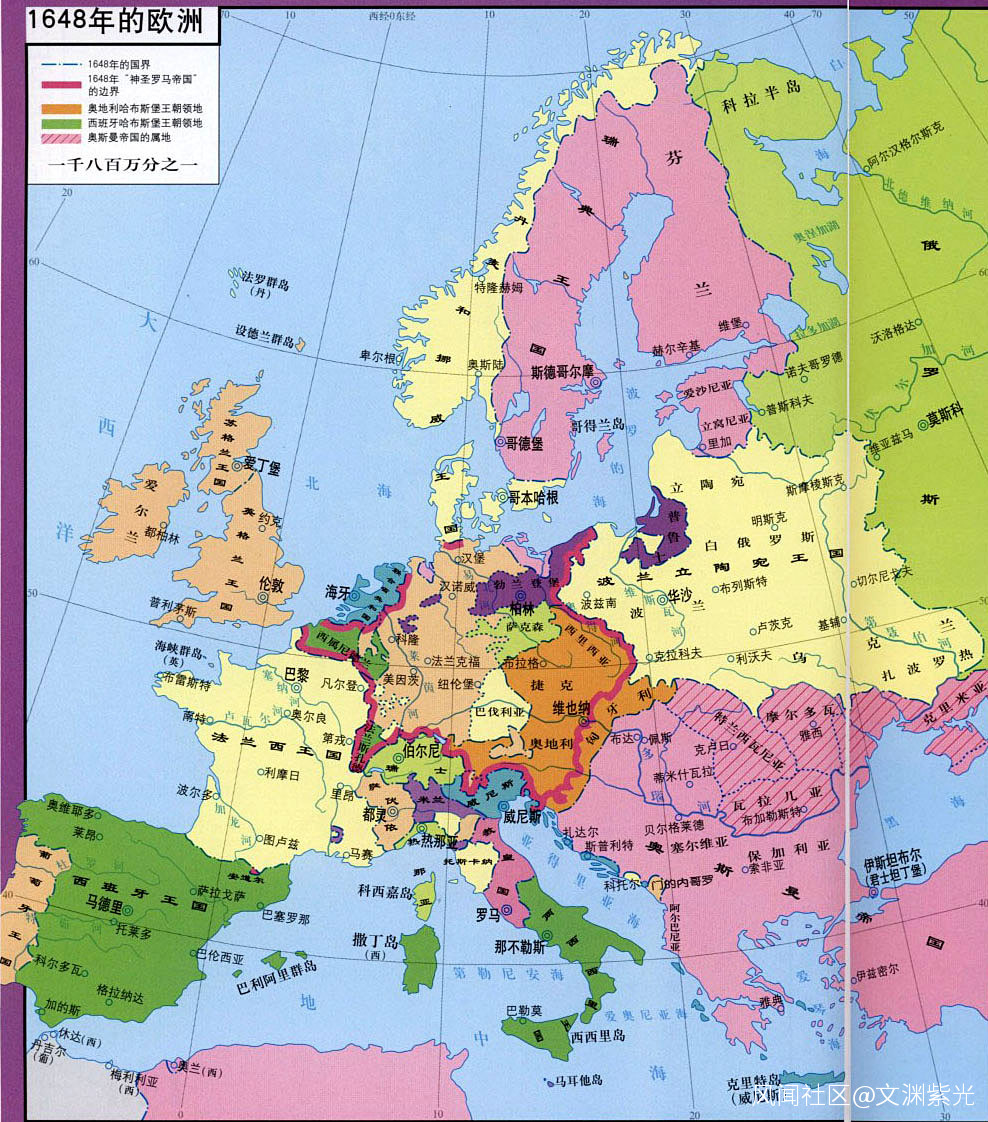
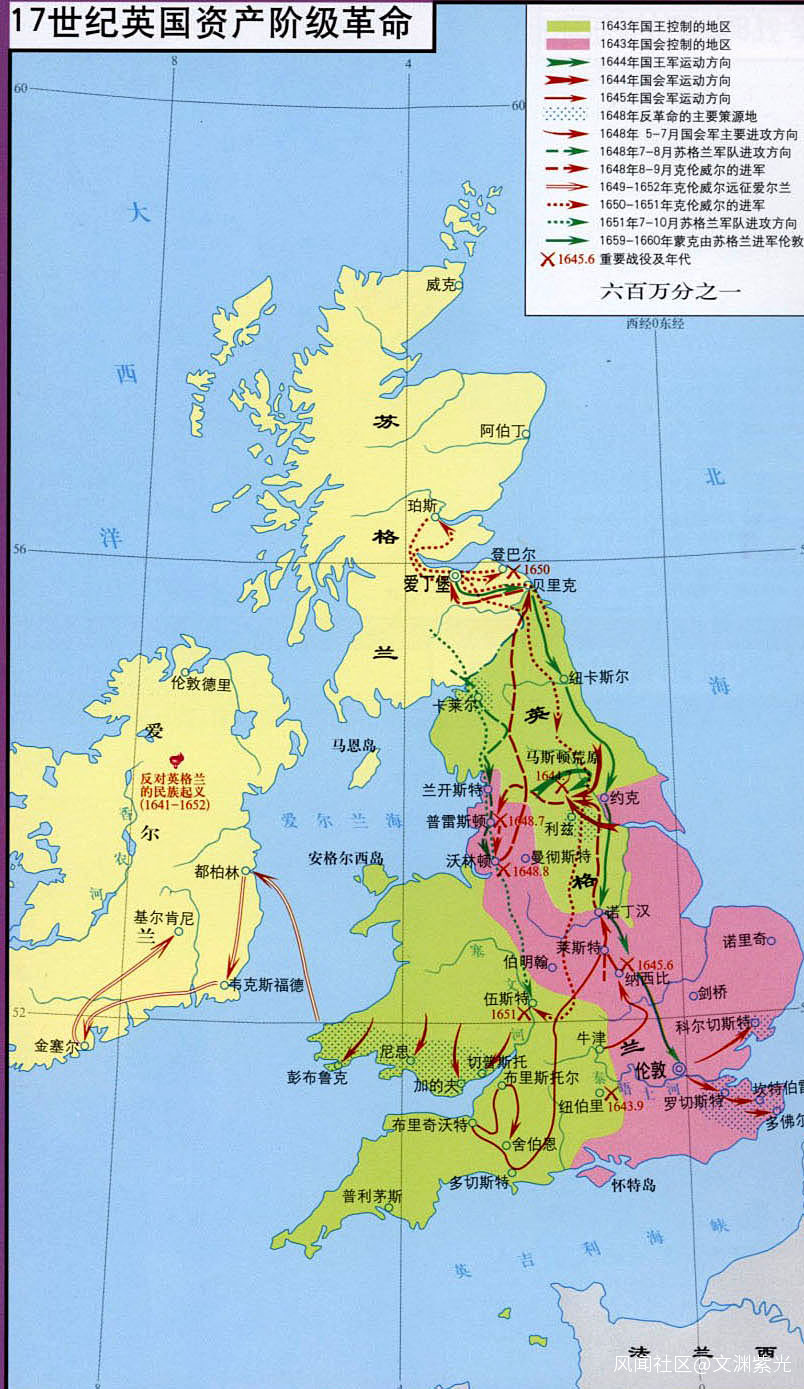
    15、17 世紀初，蘇格蘭納皮爾在《奇妙的對數》中闡述了對數方法，減輕了天文學的計算工作量。同時，笛卡爾和費馬分別發明了解析幾何。

中國的同期進展：  1667年（清朝康熙六年），因“曆獄”而被羈押在廣州的包括耶穌會、道明會、方濟會會士共23人召開了一場長達四十天的會議，討論在華傳教的方針，最後通過的決議之一，是遵守1656年（清朝順治十三年）教皇的裁定。其中道明會士 閔明我 始終持不同意見，在獲釋後立即返歐，並於1676年（清朝康熙十五年）在馬德里出版《中國歷史、政治、倫理和宗教概觀》（西班牙語：  Tratados históricos, políticos, éticos y religiosos de la monarchia de China  ）一書上冊，三年後出版下冊，抨擊在華耶穌會士的傳教方式，羅馬的耶穌會總會於是緊急將該書寄至中國，並要求各地的會士傳閲並提供駁斥的論據。羅馬教廷經過討論，決定不更改1656年的命令。

1687年（清朝康熙二十六年），法國國王路易十四派遣耶穌會士洪若翰、李明、張誠、白晉、劉應以**“國王數學家”**的名義赴華，在經歷與葡萄牙籍傳教士的鬥爭後，耶穌會在華法國傳教區終於成立，首任會長為張誠。該會成員大多贊成所謂“利瑪竇規矩”。只有劉應持反對意見。

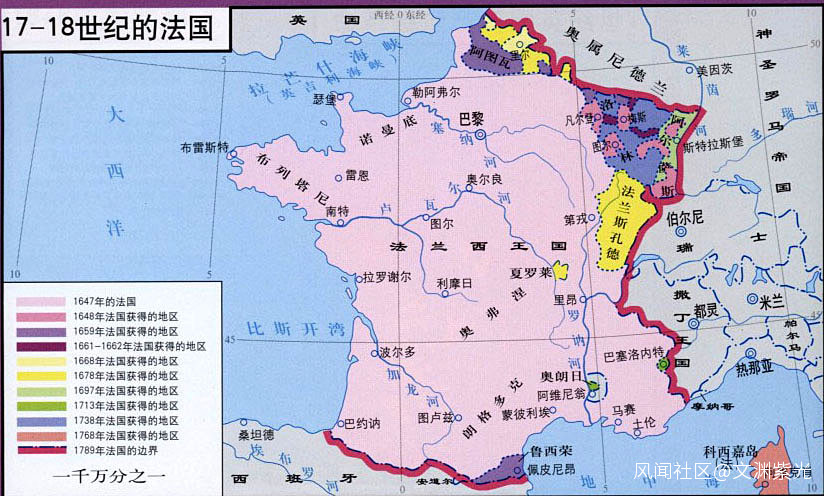
1693年（康熙三十二年）3月26日，巴黎外方傳教會的顏璫主教打破各方妥協，在他所管轄的福建代牧區內，發佈了禁止中國教徒實行中國禮儀的禁令，自此爭議迅速擴大，**由純宗教學術問題，逐漸演變成為清王朝和羅馬教廷之間的國家政治之爭。**羅馬教廷在1701年（康熙四十年）和1719年（康熙五十八年）先後派鐸羅（  Charles-Thomas Maillard De Tournon  ）和嘉樂（  Carlo Ambrogio Mezzabarba  ）兩位特使來華，期間也發佈了一系列的禁教令。鐸羅 使華 以失敗而告終，自1720年12月31日起嘉樂來華後康熙接見嘉樂宗主教前後共十三次 ，禮遇很隆，對於敬孔敬祖的問題，當面不願多言，也不許嘉樂奏請遵行禁約。嘉樂宗主教因有了鐸羅的經歷，遇事很謹慎。看到事情不能轉圓時，乃奏請回羅馬。

     16、**17 世紀牛頓和萊布尼茨獨立發明微積分。微積分被譽為人類精神的最高勝利。牛頓證明了積分與微分的互逆關係。**牛頓萊布尼茨微積分發明之爭：發明時間牛頓早於萊布尼茨；發表時間萊布尼茨（1684年）早於牛頓（1687年，原理）。牛頓在《原理》中為微積分披上的幾何外衣使他的流數術僵硬呆板，固守牛頓的幾何形式，阻礙了 18 世紀英國數學的發展；萊布尼茨的微積分符號（∫，dx）很精心並沿用至今，牛頓符號中用點.表示流數（微分），撇’表示流量（積分）已被淘汰；牛頓三大力學定律和萬有引力定律，萊布尼茨二進制。微積分，對數和解析幾何被恩格斯稱為 17 世紀數學三大重要成就。

清朝1644--1911年

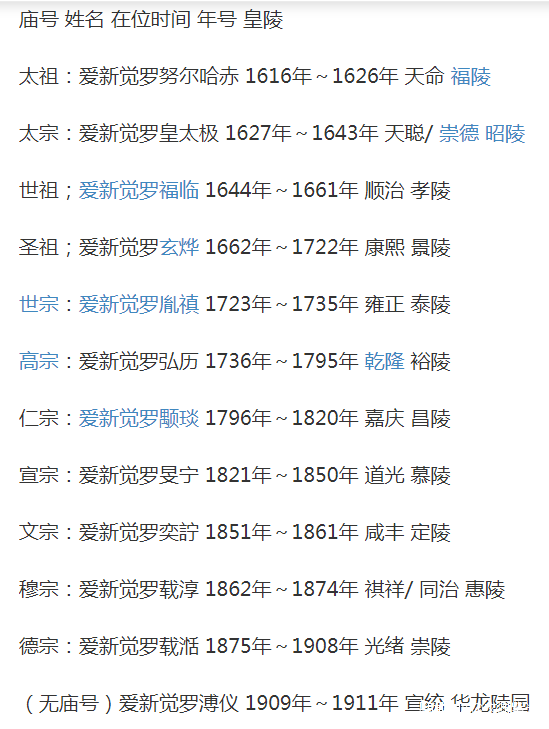
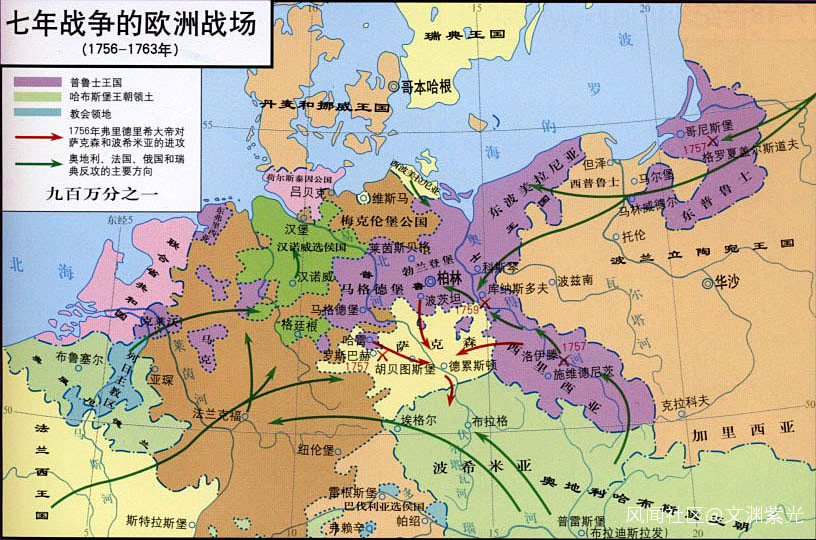
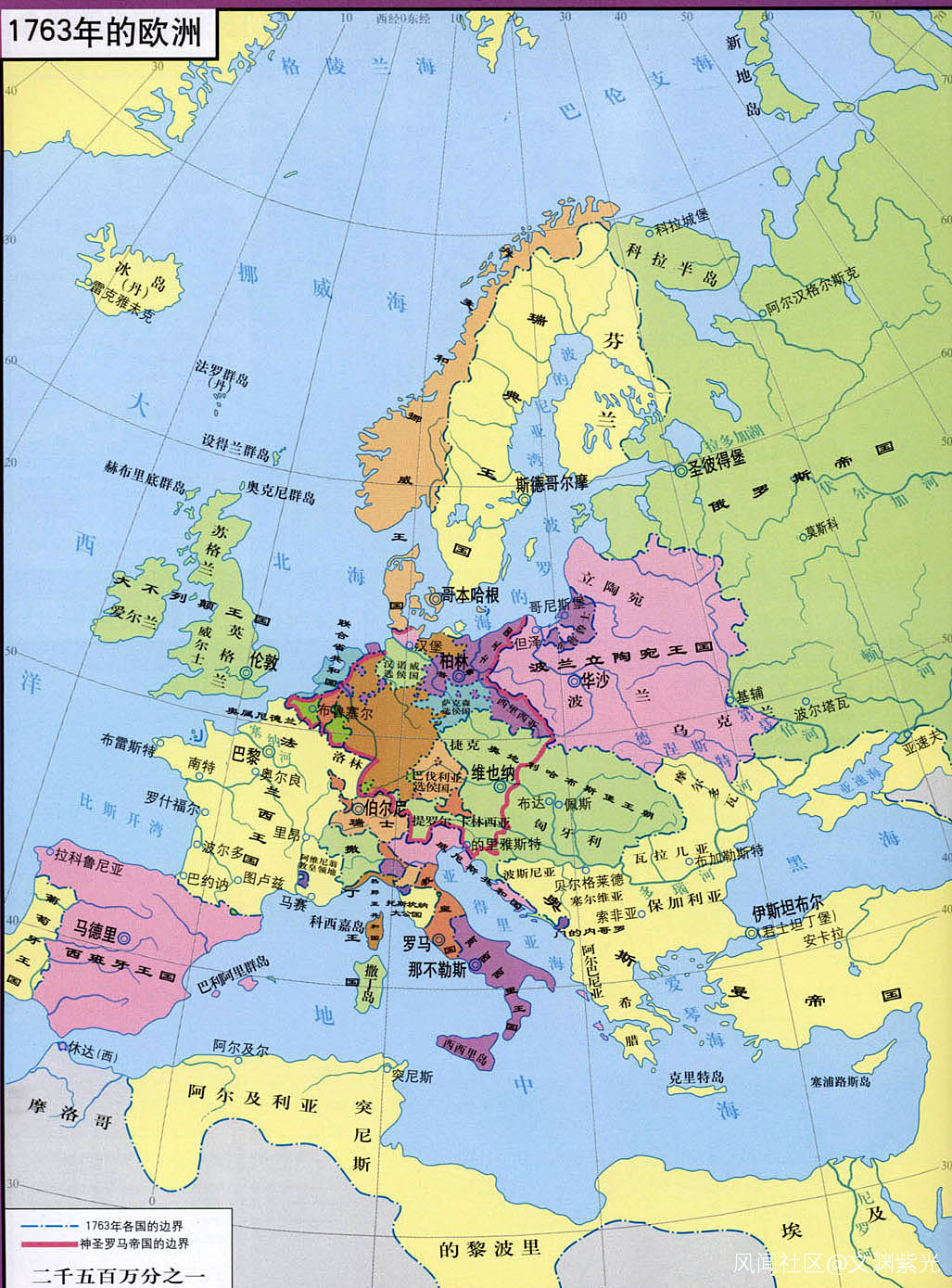
     17、18 世紀微積分進一步深入發展：泰勒，麥克勞林等發展研究了牛頓的流數術，歐陸數學家有伯努利兄弟，歐拉，克萊洛，達朗貝爾，拉格朗日，拉普拉斯，勒讓德，蒙日。

     18、18 世紀，費馬提出費馬大定理等開始研究數論，哥德巴赫給歐拉寫信，提出猜想：每個偶數是兩個素數之和；每個奇數是三個素數之和。拉格朗日指出用根式求解解 4 次以上的方程是不可能的，但未給出證明，19 世紀後被挪威年輕人阿貝爾（27 歲肺結核去世）證明，並引入了“域”這一重要的近世代數概念。後來法國數學家伽羅瓦（21 歲死於與政敵的愛情糾葛引起的決鬥）給出了能用根式可解的特殊方程的充要條件，並提出了最早的羣的定義，導致代數學的新生。但伽羅瓦的論文曾三次向法國科學院遞交：第一次被柯西丟失；第二次傅里葉病逝下落不明；第三次泊松認為不可理解打入冷宮。決鬥前夜，伽羅瓦整理了數學手稿，並在遺書中堅信“總會有人發現（14 年後），解釋清楚這堆東西對他們是有益的”愛爾蘭數學家哈密頓在推廣複數的時候，發現了四元數：a+bi+cj+dk（丟失了乘法的交換性），麥克斯韋把四元數分為數量和向量部分。向量部分的三個分量解釋成三個座標軸的長度。美國吉布斯和英國亥維賽拋棄四元數的數量部分，提出向量：v=ai+bj+ck線性代數起源於線性方程組求解中的行列式和矩陣，19 世紀開始獨立發展，柯西，凱萊和西爾維斯特等發展了行列式，矩陣理論。

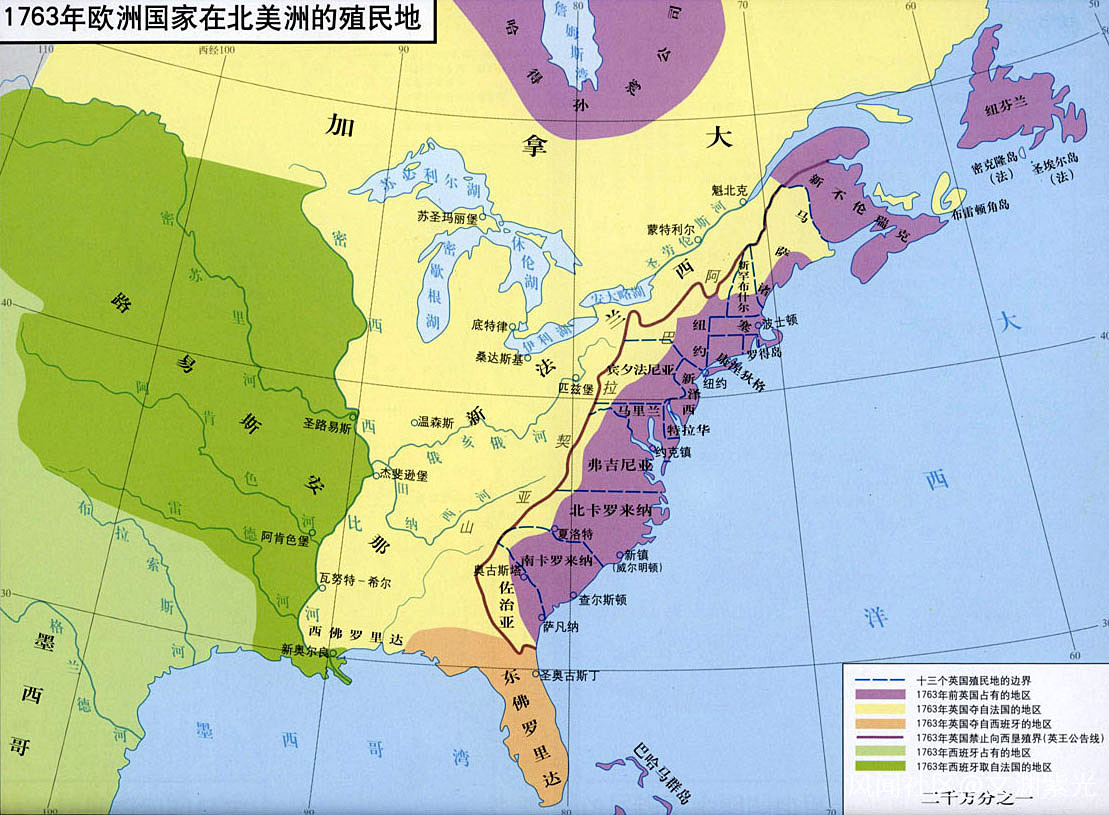
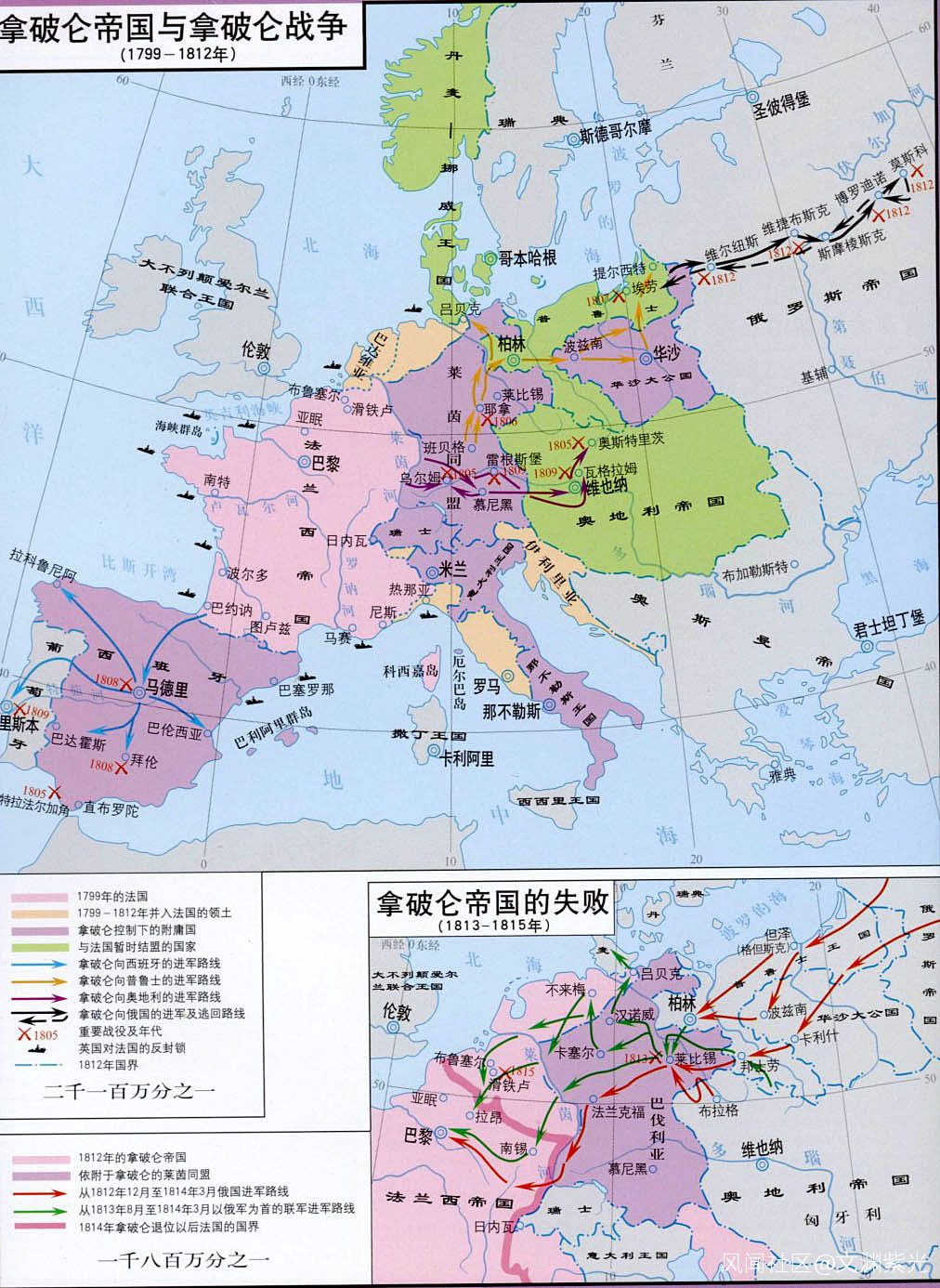
     19、 19 世紀中葉，英國布爾在 1847 和 1854 年出版的《邏輯的數學分析》和《思維規律研究》中闡述了布爾邏輯代數思想。

     20、 1840 年，俄國羅巴切夫斯基發表非歐幾何的德文著作，其基本思想與高斯，波約是一致的，被稱為幾何學中的哥白尼，遭到羣起而攻之。1854 年黎曼（不到 40 歲肺結核去世）在羅氏幾何，高斯的內藴微分幾何基礎上建立了更廣泛的黎曼幾何，歐氏幾何和羅氏幾何和黎曼幾何對應了三維空間的曲率為 0，負和正。

     21、1872 康托爾發表集合理論，並證明了有理數可數，實數不可數，為超窮集合理論邁出了堅實一步。

     21、1900 年 8 月，希爾伯特在國際數學家大會上作了題為《數學問題》的演講，提出了 23 個數學問題（包括黎曼猜想，哥德巴赫猜想，孿生素數猜想，），來開了 20 世紀數學的序幕。

     22、2000 年 5 月 24 日美國克雷數學研究所(Clay Mathematics Institute,CMI)公佈數學猜想：千禧年大獎難題(MillenniumPrize Problems), 又稱世界七大數學難題。根據克雷數學研究所訂定的規則，任何一個猜想的解答，只要發表在數學期刊上，並經過兩年的驗證期，解決者就會被頒發一百萬美元獎金。這些難題是呼應 1900 年德國數學家大衞·希爾伯特在巴黎提出的 23 個數學問題。包括了龐加萊猜想（其中三維的情形被俄羅斯數學家格里戈裏·佩雷爾曼於2003 年左右證明。2006 年，數學界最終確認佩雷爾曼的證明解決了龐加萊猜想。Clay 數學研究所在 2010 年為此召開特別會議，為此猜想蓋棺定論。佩雷爾曼拒領菲爾茲獎和千年問題獎。），霍奇猜想，黎曼猜想等。

現代數學獎：菲爾茲獎（1.5 萬美元，四年一次，40 歲下），沃爾夫獎（10 萬美元，每年一次，40 歲以上），阿貝爾獎（80 萬美元，每年一次），千年問題獎（100 萬美元），陳省身獎（25 萬美元+25 萬美元，四年一次）等。