嫌我們理科生不夠浪漫?你有一份音樂數學入門指南待查收_風聞
中科院物理所-中科院物理所官方账号-2020-07-26 12:00
某天小編閒來無事瀏覽今年的高考題,全國卷II文科數學一道與鋼琴相關的題成功引起了我的注意。大家總覺得我們理科生不懂浪漫,這道題看起來可以替我們評評理。

作為理科生,看到數學題自然是很興奮地先解題,列舉法可以很簡單粗暴地給出答案:
發現原位大三和絃和原位小三和絃在一組音中一共有10種情況,所以答案選C,你做對了嗎?
做完題小編不禁開始思考音樂背後的物理和數學原理,為什麼鋼琴一組音有7個白鍵5個黑鍵,和絃為什麼是這樣排列的?
什麼是聲音?
初中物理中我們就學過聲音是由振動產生的聲波,可以通過介質(空氣、固體或液體)以波的形式傳播被人耳或者其它接收器感知。在自然界中能為人的聽覺所感受到的音是非常多的,人耳能識別頻率在20Hz~20000Hz的聲音,但並不是所有的聲音都能作為音樂的材料。那麼什麼樣特別的聲音可以用來搞音樂呢?

我們知道聲音有高低、強弱、長短、音色等四種性質。振動發聲就會產生一定的頻率(Hz),對應的便是音高,而其傳播的能量大小對應的是音強(dB)。由於發聲體材料特性不同,會產生不同的音色,音色是一個比較玄學複雜的東西,它與發聲體的性質、形狀及其泛音的多少有關,比如二胡和鋼琴彈撥同一個音給人的體驗是完全不同的,比如班主任和小芳喊你名字給你的感覺也是不同的。
音強、音高、音色可以通過音頻圖像展示出來,音強對應的是其振幅大小,與彈撥樂器的力度有關;音高對應的是頻率高低,一般情況下樂音是固定頻率的;而音色是伴隨着主音高一些附加的頻率,與樂器的種類、材質、狀態等有關。
音頻圖像(圖源:QIPOST《鋼琴音色的物理學》)
並不是所有的聲音都好聽,好聽的是樂音,不好聽的是噪音,但是蘿蔔青菜各有所愛,如何更標準地區分樂音和噪音呢?我們可以簡單地根據聲音振動狀態的規則與不規則來定義樂音與噪音。在音樂中所使用的主要是樂音,並由一堆有規律的固定音高的音組成樂音體系。
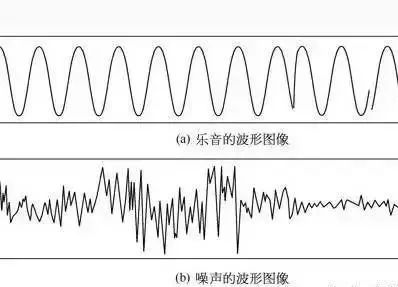
樂音與噪聲的波形圖(圖源:神州音響網)
樂音體系中的數學規律
樂音體系中的音,按照上行或下行次序排列起來叫做音列。在標準調音下,鋼琴這種頻率固定、音域廣泛的樂器成功引起了小編的注意,於是我去搜了普通鋼琴八十八鍵的頻率對照圖,可以從中明顯地看出樂音體系所使用的音和音列。
鋼琴八十八鍵的頻率對照圖 (圖源:CSDN《基礎樂理和鋼琴》)
從中我們可以發現第n個鍵所對應的頻率為:
這裏使用的頻率計算方法便是大名鼎鼎的十二平均律。從表中可以發現頻率比為整數倍的兩個音具有同樣的音名(現代音樂用字母CDEFGAB來標記),兩個相鄰的具有相同音名的音音程相差八度。音程指兩個音在音高上的相互關係,也可以理解為兩個音頻率的“距離”。在十二平均律中將八度的音“平均”分為了十二個部分——半音。相鄰半音之間的頻率比等於一個常數:
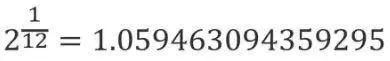
十二平均律早在古希臘便有人提出了,但並未加以科學的計算。世界上最早根據數學來制定十二平均律的是我國明朝大音樂家朱載堉(1584年)。

朱載堉:《樂律全書》
為什麼是十二平均律?或許大家和小編都有這樣的疑問,帶着這樣的問題我們來一起探討。
泛音與諧波的關係
相同音名頻率之間的整數倍關係不得不讓我們想到了在物理學中諧波這個概念,諧波是指週期函數或週期性的波形中能用常數、與原函數的最小正週期相同的正弦函數和餘弦函數的線性組合表達的部分,其頻率是基頻的整數倍,可通過傅里葉變換來得到。
“傅里葉”這三個字想必大家都不陌生,如傅里葉變換、傅里葉積分、傅里葉級數、傅里葉分析…不少理工科的同學為此飽受折磨,並留下了心理陰影(這個陰影也可以進行傅里葉變換喔~),逃不掉的都是命運。

傅里葉變換是一種線性積分變換,用於信號在時域(或空域)和頻域之間的變換,在物理學和工程學中有許多應用。因其基本思想首先由法國學者約瑟夫·傅里葉系統地提出,所以以其名字來命名以示紀念。簡單來説傅里葉變換就是將一個複雜的波形拆開成一個個正弦波的組合,實際上傅里葉變換就像化學分析,可以確定波的基本成分。
傅里葉變換將函數的時域(紅色)與頻域(藍色)相關聯。(圖源:維基百科)
在鋼琴中彈響一個音,都不只是一個音在響,而是許多音的結合,這種聲音叫做複合音,複合音可以通過傅里葉分析拆分成單音****。複合音的產生是由於發音體(以弦為例)不僅全段在振動,它的各部分(二分之一、三分之一、四分之一等)也分別同時在振動。由發音體全段振動而產生的音叫做基音,也就是最易聽見的聲音,由發聲體各部分分段振動而產生的音叫做泛音,其實就是物理學上的諧波,基波頻率2倍的音頻稱之為一次泛音,基波頻率3倍的音頻稱之為二次泛音,以此類推。
諧振現象(圖源:維基百科)
這些泛音是聽覺不易聽出來的,但是由於共振(在聲學中亦稱“共鳴”),可以在鋼琴對應鍵的鋼弦上觀察到其振動,這也是一個直觀的傅里葉分解。共振指的是物體在特定頻率下會比其他頻率以更大的振幅做振動,比如兩個頻率相同的音叉靠近,其中一個振動發聲時,另一個也會發聲。
它們與基音之間的音程以及頻率比是固定的:音程是一個八度(頻率比為2:1),然後是一個純五度(頻率比為3:2),等等。一件樂器的音色是由其泛音的比例決定的,泛音離不開基音,否則就是無本之木了,泛音和基音一同共鳴,才形成了豐滿完整的音色。
十二平均律與五度相生律的故事
由於複合音中的泛音與基音相處融洽和諧,根據複合音的第二分音和第三分音的純五度(頻率比為3:2)關係,即由某一音開始向上推一純五度,產生次一律,再由次一律向上推一純五度,產生再次一律,如此繼續相生產生了五度相生律。
在此做一個簡單的計算來推導五度相生律:
取一基音,以C為例,將其頻率f乘上3/2,即升高完全五度得下一音G。
將G升高完全五度得下一音D,D之頻為(3f/2)*(3/2)=9f/4,高於原基準音之倍頻,故將其除二,即降八度得9f/8。
將D升高完全五度得下一音A,A之頻為(9f/8)*(3/2)=27f/16。
將A升高完全五度得下一音E,E之頻為(27f/16)*(3/2)=81f/32,高於原基準音之倍頻,故將其降八度得81f/64。
將E升高完全五度得下一音B,此時B之頻為(81f/64)*(3/2)=243f/128。
假設有一音升高完全五度再降八度後為基準音C,可得此音之頻為4f/3,此即為F。
依上法可得七聲音階,整理可得下表:
由於
(m, n為正整數),隨着純五度的演進最後得到的音無法還原閉合,造成了音樂律學上的困難與妥協。並且五度相生律決定的音程之間頻率比不統一,雖然大部分五度之間的音聽起來是非常和諧的,但也有一部分不和諧的音存在。由五度相生律確定的音也面對一大難題,便是在樂曲轉調的時候聽起來也會很彆扭,這也是導致了人們試圖尋找其它的音律。
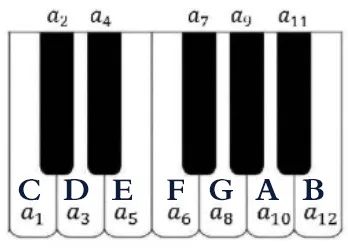
音名與琴鍵的對應關係
隨着時代的發展,復調音樂(有兩條及以上獨立旋律)佔了越來越多的比重,轉調也因此變得更加重要。為了解決轉調的難題,作曲家們嘗試更優化的律法,十二平均律脱穎而出。十二平均律將**八度的音程按頻率比例分成十二等份,讓兩個相鄰半音的頻率比等於一個常數,即2的1/12次方。**由於它純五度兩個音的頻率比
,人耳基本上聽不出“五度相生律”和“十二平均律”的五度音程的差別,由此十二平均律在交響樂隊和鍵盤樂器中得到廣泛使用。
在鋼琴中黑鍵與白鍵其實並無本質上的區別,音色完全一樣,相鄰琴鍵間(j-i=1)的頻率比都為2的1/12次方。白鍵是音的原型(自然中找得到的音),七個琴鍵構成基本音級(CDEFGAB),黑鍵是根據基本音級升高或降低一個半音而得到的音構成變化音級。由於黑鍵很規律的兩個一組和三個一組排列,我們可以很方便地在鋼琴中找到各個音的位置,鋼琴小白也可以看着簡譜演奏一段《小星星》。
和絃的起源
提到和絃,可能不少曾夢想仗劍走天涯的少年都擁有一把撲灰吉他,但棄於大橫按,吉他伴奏主要是由幾個和絃構成,那麼你們有想過和絃是什麼嗎?

小編的撲灰吉他
通過十二平均律定義的現代鋼琴,一組琴鍵由7個白鍵和5個黑鍵組成,已知相鄰琴鍵之間的頻率比:
按照和聲音程(同時彈奏的兩個音形成和聲音程)在聽覺上所產生的印象,音程可分為協和和不協和兩類。
協和音程顧名思義是聽起來悦耳、融合的音程。協和音程可分為三種(音程以第ai與aj個琴鍵來表示):
極完全協和音程:聲音完全合一的純一度(j=i)和幾乎完全合一的純八度(j-i=12)
完全協和音程:聲音相當融合的純五度(j-i=7)和純四度(j-i=5)
不完全協和音程:即很不融合的大三度(j-i=4)、小三度(j-i=3)、大六度(j-i=9)、小六度(j-i=8)。
極完全協和音程與完全協和音程的特性是聲音有點空,而不完全協和音程的聲音則較為豐滿,可配合視頻感受。
不協和音程聽起來比較刺耳,彼此不是很融合,比如大二度(j-i=2)、小二度(j-i=1)、大七度(j-i=11)、小七度(j-i=10)。
正因為這些聽起來和諧的聲音給人舒適放鬆的感覺,作曲家們便想辦法將其組合起來,把它們按照三度(大三度(j-i=4)、小三度(j-i=3))關係排列起來的三個以上的音結合起來構成和絃。按三度音程關係構成的和絃,由於各音間保持一定的緊張度,音響協調豐滿,併合乎泛音的自然規律,因而被廣泛採用。
最後再回到這道題目上來,瞭解一下什麼是原位大三和絃和原位小三和絃。原位和絃指以和絃的根音為低音(最低的音)的和絃,由三個音按照三度關係疊置起來的和絃叫做三和絃,在鋼琴中的12個鍵依次記為a1,a2,…,a12 ,設0<i<j<k<13 ,大三和絃中j-i=4 表示根音到三度音是大三度,k-j=3 表示三度音到五度音是小三度,k-i=7 表示根音到五度音是純五度。同理,小三和絃中 j-i=3 表示根音到三度音是小三度,k-j=4 表示三度音到五度音是小三度, k-i=7 表示根音到五度音依然是純五度。
寫完這些,小編不禁看了看在角落落灰的燒火棍,根據今天所學的樂理知識,可以來一段單絃演奏~
參考資料:
[1] 李重光. 《音樂理論基礎》
[2] 卓仁祥. 從文化史角度看十二平均律的發現
[3] 五度相生律,維基百科
[4] 十二平均律,維基百科











