讓中央集體學習的量子科技究竟是啥?這個科普我已經做了五年(四)_風聞
风云之声-风云之声官方账号-2020-12-10 08:25
導讀
分解300位和5000位的數字,量子算法會把所需時間從15萬年減到不足1秒鐘,從50億年減到2分鐘!
視頻鏈接:
西瓜視頻:
https://www.ixigua.com/6902292563307266573
本視頻發佈於2020年12月4日,播放量已超百萬
前三次我們説到,中央集體學習的量子科技,主要指的是量子信息(讓中央集體學習的量子科技究竟是啥?這個科普我已經做了五年(一)量子是什麼 | 袁嵐峯)。它分為量子通信和量子計算兩大領域,正如我們平時用的手機屬於通信,計算機屬於計算。這次我們就來講解量子計算。
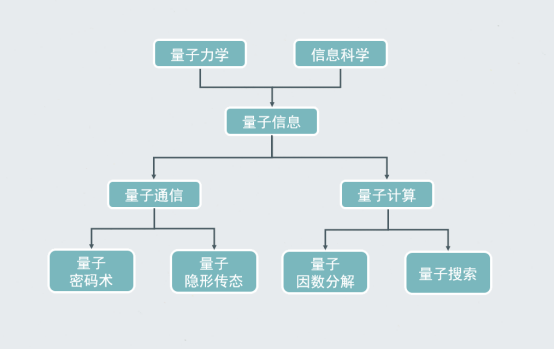
量子信息學科內容
你可能早已聽説過,量子計算是真正的顛覆性技術,能夠做到很多現有的計算機做不到的事。但是,量子計算為什麼這麼厲害呢?很奇妙,大多數人的理解都是錯誤的。
媒體常見的説法是:量子計算機的運算速度特別快,比經典計算機快得多。這聽起來很容易理解,就好像486比386快,386比286快。如果媒體想解釋原理,還會説這是因為量子計算機是並行計算,一次能處理很多任務,而經典計算機一次只能處理一個任務。
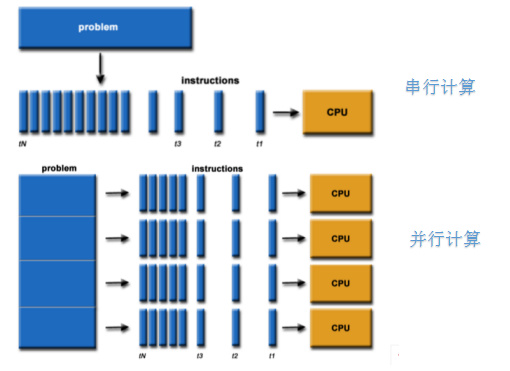
並行計算
然而,這種話只能矇住外行。如果你對計算機科學稍有了解,你立刻就知道,並行計算並不是什麼特別的東西,現在的計算機就經常在用。例如所有的超級計算機,神威太湖之光、天河二號等等,都是用大規模並行計算達到超高速度的(中國超算全自主,重奪第一已出發 | 袁嵐峯)。

神威太湖之光
所以,量子計算真正的原理是什麼?我來向大家解讀一下。
這裏的關鍵在於,量子計算機不是幹什麼都特別快,而是隻對某些問題特別快,因為對這些問題能設計出快速的量子算法。也就是説,量子計算機優於經典計算機,並不是像486優於386那樣幹什麼都強,而是好比你的計算機能運行某個遊戲,而別人的計算機不能運行這個遊戲,所以在這方面你的計算機強。
量子計算機為什麼會有這樣的優勢呢?原因就在於量子力學三大奧義:疊加、測量和糾纏(讓中央集體學習的量子科技究竟是啥?這個科普我已經做了五年(二)量子力學三大奧義 | 袁嵐峯)。這是我們在前面兩期中講的,不瞭解的同學們請回去複習一下。
最基本的道理是,經典計算機的基本操作單元是比特,而量子計算機的基本操作單元是量子比特。比特好比開關,只有開和關兩個狀態。而量子比特好比旋鈕,有無窮多個狀態。所以顯然,量子比特有可能做到比經典比特更多的事。
具體而言,量子比特超越經典比特的辦法是這樣的。
如果有n個經典比特,每一個有兩個狀態,它們的組合就總共有2n個狀態。如果想知道一個操作對n個比特產生的效果,就需要把這個操作作用到這2n個狀態上,把所有的結果都試一遍。也就是説,需要2n次操作。
2n是個增長非常快的函數。學過數學的人都知道,指數增長比任何的多項式增長都要快,比如説比n10000都快。所以隨着n的增長,經典計算機的計算量很快就會爆炸。
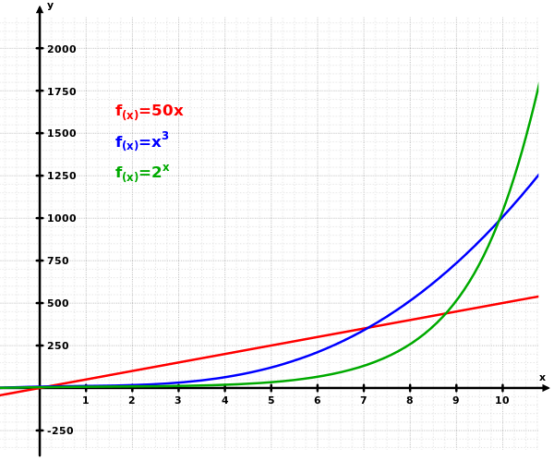
指數增長比任何的多項式增長都要快
但對於量子比特,事情就不一樣了。一個量子比特有兩個基本狀態,一個一般的狀態等於這兩個基本狀態的疊加。對於n個量子比特的體系,基本狀態有2n個,一個一般的狀態等於這2n個基本狀態的疊加(讓中央集體學習的量子科技究竟是啥?這個科普我已經做了五年(三)量子糾纏 | 袁嵐峯)。
也就是説,n量子比特體系的一般狀態可以寫成
c(000…) |000…> + c(100…) |100…> + c(010…) |010…> + … + c(111…) |111…>,
其中每一個c都是一個係數,總共有2n個這樣的係數。
現在重點來了:對這樣一個一般的狀態做一次操作,就可以同時改變2n個係數,相當於對n個比特的經典計算機進行了2n次操作。一個頂2n個!
這是一個嚇死人的優勢。所謂量子計算機的優勢來自並行計算,實際指的就是這個意思。如果使用得當,這可以帶來指數級的加速。原來需要上億年的任務,現在可能一秒鐘就能搞定,這是多麼驚人的進步!
但是且慢,這一切有個前提,“如果使用得當”。什麼意思呢?因為把數據讀出來是大問題。
你要把這2n個數據讀出來,就需要做測量。但我們前面講過,測量的時候體系的狀態會發生突變,落到某一個基本狀態上面。結果就是,你雖然一下子獲得了2n個數據,但讀出的時候又只剩下一個了(量子計算機強在哪裏?不是因為能存下全世界的信息 | 袁嵐峯)。
因此,量子計算確實具有巨大的優勢,但這是個潛在的優勢,需要非常巧妙的算法才能發揮出來。只對少數特定的問題,人們設計出了這樣的算法。而對於大多數的問題,量子計算還沒有表現出任何優勢。
你也許會感到很失望,原來量子計算沒什麼用啊?別急。目前已知的能發揮量子計算優勢的問題雖然不多,但其中有些就非常重要,例如因數分解(factorization)和無結構數據庫的搜索。下面,我們就來解釋一下量子因數分解。
因數分解是什麼?就是把一個合數分解成質因數的乘積,例如21 = 3 × 7。只需要小學數學水平,就能理解這個概念。但重點在於,因數分解是一個經典的數學難題。
你也許會感到很奇怪,這有什麼難的?吶,分解一個小的數字當然很容易,你不管三七二十一就能分解21。但是來分解下面這個數看看:
267 - 1 = 147, 573, 952, 589, 676, 412, 927。
這是一個21位數。它是質數還是合數呢?這就遠不是一眼能看出來的了。
1644年,也就是李自成進北京、明朝滅亡的那一年,法國數學家梅森(Marin Mersenne,1588 - 1648)提出這個數是一個質數。

李自成

馬林·梅森
在那之後的很長時間裏,人們都這麼認為。直到1903年,清朝都快亡了,人們才發現它其實是一個合數,等於
193, 707, 721 × 761, 838, 257, 287。

大清亡了
為了分解這個21位數,消耗了一個朝代的時間!
因數分解為什麼這麼困難呢?因為沒有特別高效的算法。
如果讓我們分解一個數字N,我們能夠想到的最簡單的算法,就是從2開始一個個往上試。先問:它能不能被2分解?如果不能,再問:它能不能被3分解?這樣一個個試,直到根號N為止。如果到根號N都分解不了,説明它是個質數。由此可見,嘗試的次數大約是根號N。
這是個特別簡單也特別愚笨的算法。如果N表示成二進制有n位數,也就是N約等於2n,那麼計算量就約等於根號N即2n/2。這正是指數增長,所以隨着位數的增長,計算量很快就爆炸了。
顯然,數學家不會滿足於這麼愚笨的算法。經過幾百年的研究,人們提出了很多改進的算法,目前最高效的算法叫做“數域篩”(number field sieve)。這些算法確實快了很多,然而在基本面上沒有變化,計算量仍然是指數增長的。
比如説,一台計算機每秒做一萬億次運算,它用數域篩算法分解一個300位的數字需要15萬年,分解一個5000位的數字需要……50億年!地球的年齡也不過是46億年而已!所以,因數分解仍然是一個難題。
奇妙的是,分解不開對我們是一件好事,——可以用來保密。當今世界最常用的密碼體系之一叫做RSA,它就是基於因數分解的困難性設計出來的。RSA這個名字,是三位發明者李維斯特(Ron Rivest)、薩莫爾(Adi Shamir)和阿德曼(Leonard Adleman)的姓氏首字母縮寫。

RSA密碼體系的三位發明者
大致而言,RSA的操作方式是這樣的。讓我們把信息的發送方叫做Alice,接收方叫做Bob。
首先,Bob取兩個很大的質數p和q,求出它們的乘積
N = pq。
這一步是很容易的。但是如果有人只知道N,想求出p和q,就是很困難的。
然後,Bob把N向全世界公佈,這叫做公鑰。把p和q藏好不公佈,這叫做私鑰。
註釋一下,密碼學裏的密鑰這個詞念mì yuè。鑰匙的鑰(yào)這個字是個多音字,在這裏念yuè。你去百度一下或者翻一下字典,就能找到這個答案。
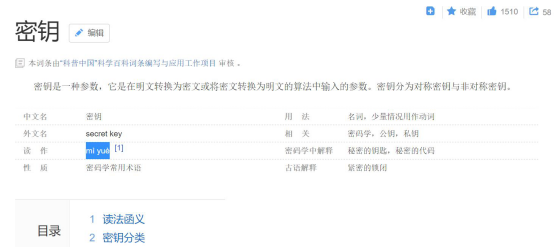
百度百科的密鑰詞條
然後,Alice把想發送的信息用公鑰N加密,用公開信道發給Bob。Bob拿到密文,用自己的私鑰p和q就可以解密。其他人雖然拿到了密文,但分解不開N,算不出p和q,所以無法竊密。
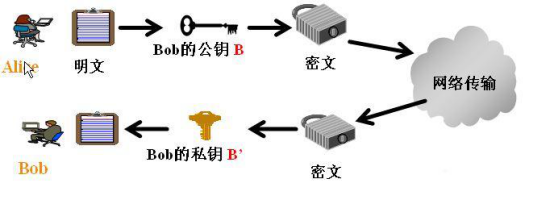
公鑰密碼體制
這確實是一個非常巧妙的思想。在這個意義上,我們平時的網購、網上銀行、瀏覽網站等習以為常的做法,都是依靠因數分解的困難性保駕護航的。經常有無知的人説,學數學有什麼用,又不能用來買菜。但實際上,如果沒有數學,你買菜的時候錢早就被別人轉走了!
然而,RSA真的可靠嗎?這其實並沒有證明,只是個經驗而已。
永遠不能排除這種可能:將來有個聰明人發明一種高效的算法,一下子就解決了因數分解。甚至還有可能,這樣的算法已經發明出來了,只不過沒有公佈。
設想一下,如果你是美國情報部門的領導人,你的手下有人發明了破解RSA的算法,你會公佈嗎?顯然,你更可能採取的做法是悶聲發大財,在暗中破解別人自以為安全的密碼。
斯諾登爆料五眼聯盟
如果説這些擔心是“隱患”,那麼量子計算已經帶來了一個“明患”。前面談的因數分解算法都是經典計算機上的算法,其中最高效的是數域篩。但是在1994年,美國科學家肖爾(Peter Shor)提出了一種高效的量子因數分解算法。

彼得·肖爾(http://www-math.mit.edu/~shor/)
高效到什麼程度呢?分解一個n位數的計算量大約是n2。跟以前的指數增長相比,這是一個指數級的節約。舉個例子,同樣還是分解300位和5000位的數字,量子算法會把所需時間從15萬年減到不足1秒鐘,從50億年減到2分鐘!
現在,大家明白量子計算的威力了吧?
許多媒體説,量子計算機可以破解全世界所有的密碼。這話基本是可以成立的,很有可能現在的各種密碼都會被量子計算破解。不過要加個限制條件,——除了量子密碼之外。
只有魔法才能打敗魔法,只有量子才能打敗量子。量子密碼保密的基礎是物理原理,而不是數學,所以即使是量子計算也無法破解。關於量子密碼,我們會在後面介紹。
話説回來,量子計算只是在算法層面破解了RSA。而在硬件層面,量子計算機還遠沒有達到實用的程度。迄今為止,量子分解的最大的數是
291, 311 = 523 × 557。
這是科大的杜江峯和彭新華等人在2017年實現的,他們在算法上又做了不少改進(https://arxiv.org/abs/1706.08061)。

杜江峯和彭新華等人2017年用量子算法分解291311的論文(https://arxiv.org/abs/1706.08061)
這離破解RSA有多遠呢?目前常用的RSA密鑰長度是1024,也就是説,密鑰是二進制的1024位數。上面提到的291, 311是一個十進制的六位數,換算成二進制是一個19位數,離1024位還遠。
因此,我們現在還在用RSA。但數據安全工作者都知道,這種狀況不會持續太久了。
例如谷歌CEO預測,加密技術的終結可能在5年內到來(美國哈德遜研究所發佈《高管的量子密碼指南:後量子時代中的信息安全》| 中國信息協會量子信息分會)。在我看來,無論是5年、10年還是15年,這個具體的時間並不重要,真正重要的是要意識到這個明確的趨勢,未雨綢繆。

谷歌首席執行官預測,加密技術的終結可能在5年內到來
那麼,量子計算什麼時候能實用呢?下次,我們就來介紹這方面的進展。