徐光啓《幾何原本》所述 “幾何”之稱謂 實指 今天統稱的標量_風聞

一、概論

   中西科學 會通600餘年，緣何近代以來愈發自斷文脈、強行穿鑿附會，而致 懵懂紛紜？   

義理深奧之故？ 勉強轉譯之？

非也。

蓋明白之人 旁通有限，術業專攻、比附其意，然後 遽然 傳道授業 耳。

故有 食洋不化 以致為外人所鼓惑者，自然之勢。

   常有人稱讚「幾何」一詞的翻譯是  音 意 兼顧，理由是「幾何」的讀音跟 geometry 中 geo- 的發音類似，同時「幾何」在漢語中又表示「大小、多少」的意思。這個説法靠譜嗎？  

  實際結論是附會有餘、幾無準確。 度量作為名詞稱謂，今科技著作統一有幾何量、標量、向量、矢量等這些顯然 生僻古怪的等價稱呼代替。

  當今幾何學 應正名 為 度量學，徐光啓所譯“**幾何度”一詞或《幾何原本》簡稱的“幾何”**一詞， 實指 那些可以 測而得知大小 的 度量項，今稱標量和矢量。可測而得知大小的度量項 包括有長度標示的線段、有面積標示的面、有體積標示的體。徐光啓在《幾何原本》中的清晰自定義如下四幅原文截圖：

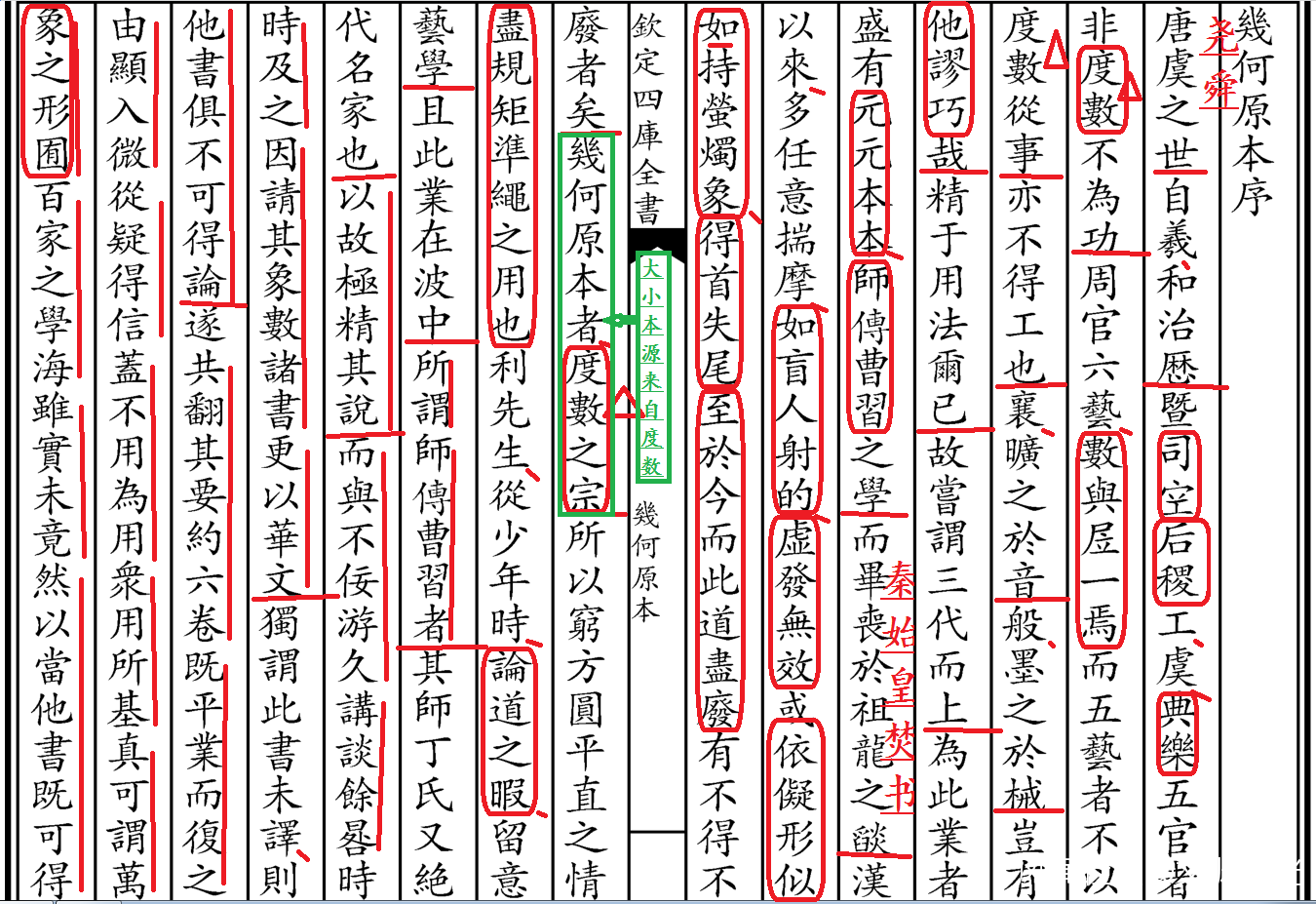
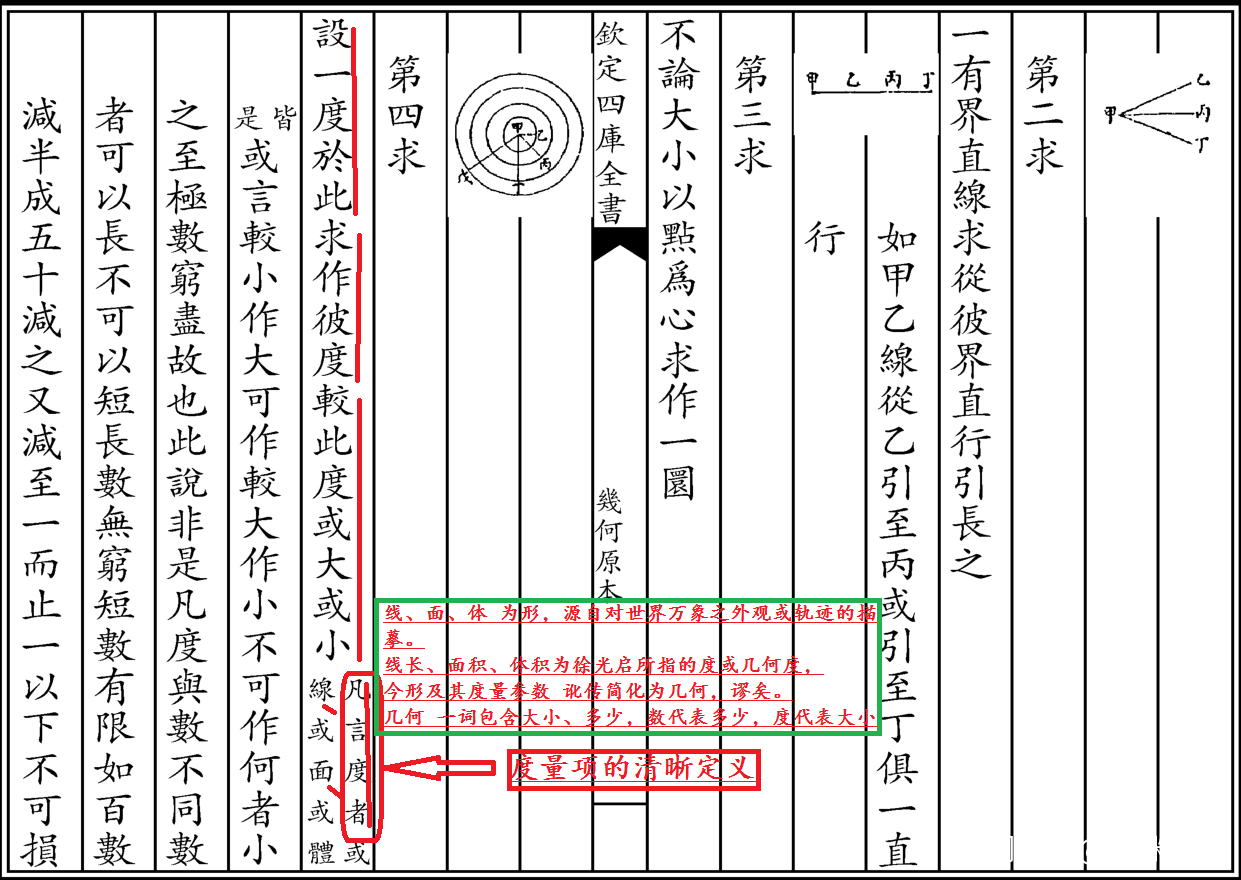
二、中國的傳統“幾何”稱謂 之實指

    在我國古代數學史上，“幾何”一詞從大約公元前186年前的《算數書》開始，一直是表示求解某數多少或某量大小的疑問詞。

表一 “幾何”一詞的含義思辨

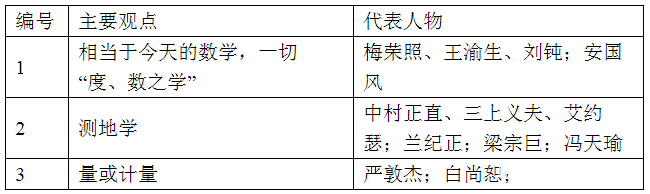
  《算數書》是1983、1984年之交出土於湖北江陵張家山247號墓一部抄寫於竹簡上的數學著作。該書的抄寫下限為公元前186年，其著作年代自然會更早些，比傳世最早的中國數學經典《周髀算經》和《九章算術》的編定至少還要早一個世紀左右。如下為竹簡整理小組整理出的釋文：

舂粟  

稟粟一石舂之為八斗八升，當益秏粟幾何？

曰：二斗三升十一分升八。

術曰：直所得米升數以為法，又值一石米粟升數而以秏米升數乘之，如法得一升。

關於“幾何”一詞的含義，即幾何一詞在漢語語境中的含義，馮天瑜先生做了精彩的考證：

    “幾何”本是漢語古典詞，義項有三：

其一，多少、若干，用於詢問數量或時間，如《詩·小雅·巧言》：“為猶將多少,爾居徒幾何？”《左傳·僖公二十七年》：“所獲幾何？”《史記·孔子世家》：“孔子居魯，得祿幾何？”劉獻廷《廣陽雜記》：“傢俬幾何？”

其二，無多時、所剩無幾，如《墨子·兼愛下》：“人之生乎地上之無幾何也。”《漢書·五行志》：“民生幾何”，注：“幾何，言無多時也。”曹操《短歌行》：“對酒當歌，人生幾何。”

其三，問當何時，如《國語·楚語下》:“其為寶也，幾何矣？”解：“幾何世也。”《漢書·五行志》：“趙孟曰：其幾何？”“注：師古曰，言當幾時也。” 

總之，“幾何”在古典漢語中是作為疑問數詞使用的。……這樣，利瑪竇便把中國士人常用的漢語疑問數詞“幾何”，改造成為一個表示物體形狀、大小、位置間互相關係的數學術語。

     但是，馮先生恰恰忽略了中國傳統數學文獻，“幾何”本來就是中國傳統數學的最常用術語，中國傳統數學典籍如《算經十書》中，作為表示求解某數量多少或大小的疑問詞，這一用法數不勝數，《九章算術》中幾乎每一道題都有它。今以徐光啓在其翻譯《幾何原本》之前的著作中所用為例：“算定勾幾何，股幾何，弦幾何，量取數處，便見何等勾股，方得免坍。”筆者做了一個統計，在這一篇僅5頁（32開）的論文中，他用了24次“幾何”這個詞，並且都是表示求解大小或多少的疑問詞或數量詞。

    另外，利瑪竇並沒有完全排斥幾何的中文原意，只是做了引申，比如，他也採用“其分者若截以為數則顯物幾何眾也，若完以為度則指物幾何大也”等説法，這裏“幾何大”、“幾何眾”意思是“數量大小”、“數量多少”。

三、“幾何”一詞外文源頭的思辨

表二  “幾何”一詞的外文來源

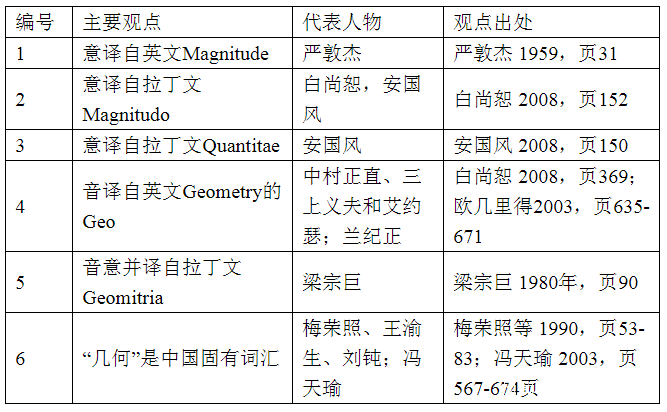
       “幾何”一詞選自中文固有詞彙，大家的認識是一致的。“幾何”一詞所對應的西學詞彙，已有研究基本使之明朗了，即“幾何”一詞意譯自拉丁文Magnitudo和Quantitae，而不是音譯。但是，仍有個別不完全一致之處，本部分以綜述前人成果為主，並擬將其理順。

       安國風將徐、利譯《幾何原本》與克拉維斯拉丁文本進行了比對，有力地證明“幾何”一詞的來源之一是，意譯自拉丁文Magnitudo。白尚恕將“幾何”唯一地對應於Magnitudo，有失全面。白認為Quantitae是“形學” ，有待商榷，Quantitae的對應英文是Quantity，漢譯為數量，筆者比對了今譯亞里士多德《工具論》（中國人民大學出版社，2003）和李之藻、傅汎際（Francisco Furtado）的《名理探》（三聯書店，1959）的相關部分，Quantitae翻譯為“數量”應是較為準確，在當時“數量”就是“幾何”。李之藻與傅汎際合譯的《名理探》明確説明“量法”譯自Geomitria：“審形學分為純雜兩端。凡測量幾何性情而不及與其所依賴者，是之謂純。類屬有二：一測量併合之幾何，是為量法，西雲日阿默第亞（Geomitria的漢語音譯）。一測量數目之幾何，是為算法，西雲亞利默第加也。”[傅汎際、李之藻 1959]

      音譯自英文****Geometry的Geo這一説法的錯誤性，嚴敦傑的研究已對其進行了糾正。其錯誤一是時間的不對應，將幾何與Geometry對應，在西方已是利瑪竇來中國一段時間以後的事，而我們在康熙時代法國傳教士白晉（Joachim Bouvet）、張誠（Jean-François Gerbillon）翻譯的巴蒂斯（Ignace Pardies）的《幾何原本》底本中，才發現“幾何”與Geometrie（此詞為法文，對應英文為 Geometry）完全對應[安國風 2008]；二是徐光啓和利瑪竇所用原文是拉丁文，而不是英文。同時這第二點也説明僅僅意譯自英文Magnitude這一説法也是不準確的。

       音譯並譯自拉丁文Geomitria這一説法也不是明末的原意。安國風已經注意到“李之藻和傅汎際合譯的《名理探》就將Geomitria音譯為‘日阿默第亞’。”[安國風 2008，頁149]但安先生在同一著作中似乎不同意將其意譯為“量法”[安國風 2008，頁151] ，值得討論。實際上，徐、利二人把這一詞彙翻譯為“量法”了，利瑪竇在《譯<幾何原本>引》中表述西方數學的基本分類：“幾何家者，專察物之分限者也，其分者若截以為數則顯物幾何眾也，若完以為度則指物幾何大也，其度與數或脱於物體而空論之，則數者立算法家，度者立量法家，”[徐宗澤 2006]在這裏他將“度者”立為“量法家”，這與克拉維斯的《導言》是一致的[安國風 2008，頁150-151]，其實在徐光啓的時代，漢字“度”的動詞含義就是今天的測量。艾儒略（Giulio Aleni）的《西學凡》（1623年刊行）也是這樣分類的：“幾何之學，名曰馬得馬第加者，譯言察幾何之道，則主乎審究形物之分限者也，復取斐祿之所論天地萬物，又進一番學問。……獨專究物形之度與數，度其完者為幾何大，數其截者以為幾何眾，然度數或脱於物體而空論之，則數者立算法家，度者立量法家，……”[艾儒略 1978]與利瑪竇的論述幾乎完全一致。

      根據耶穌會的教育體制，西方耶穌會教育計劃中的六科——文、理、醫、法、教、道，亞里士多德的邏輯學是他們的必修學科，屬於分科研修（醫、法、教、道）之前的公共必修課，教材也是統一的。所以利瑪竇所説“量法家”與傅汎際説法是一致的，即“量法家”對應的拉丁文是Geomitria。所謂Geomitria的測地學含義是埃及人的思想，在希臘人、羅馬人及其後的“利瑪竇們”那裏已變成了“量法家”。

四、與“幾何”有關的學術真實含義

表三 “幾何”一詞的含義思辨

       與“幾何”有關的學術主要有：幾何府、幾何家、幾何之學、幾何原本。幾何府，是《名理探》“十倫”之一，是今天邏輯學的一部分，它在數學原理中的應用是《幾何原本》；《幾何原本》又是徐光啓所稱的“度數之宗”，幾何家、幾何之學是《幾何原本》在度（測量）數（計算）之中的擴展。

1“幾何府”的邏輯意藴

     關於“幾何”的來歷及其在西學中的歸屬，徐光啓和利瑪竇在翻譯時採用的是“幾何府”這一説法，在徐光啓和利瑪竇的語境中，“幾何”的含義是大小，它屬於“幾何府”。他們所強調的是：“幾何”屬於“幾何府”這一邏輯學中的範疇。《幾何原本》開頭內容就是明證：“凡曆法、地理、樂律、算章、技藝、工巧諸事，有度有數者，皆依十府中，幾何府屬（“十府”指亞里士多德的十大範疇，“幾何”，今譯為標量或矢量，是其中之一）。凡論幾何，先從一點始，自點引之為線，線展為面，面積為體，是名三度（今天所説“三維）。”

     艾儒略則用“宗”來表達“府”的含義，“一門是十宗論，……（其）一為幾何，如尺寸一十等”[艾儒略 1978，頁32-33]。李之藻輯刻的《天學初函》中就有《幾何原本》和《西學凡》兩書，但他並沒有將其譯法統一，並且他和傅汎際稍後譯《名理探》時，又創造了“府”和“宗”之後的第三種譯法——“倫”。《名理探》所講“五公十倫”的“十倫之二”，即為“幾何”，是緊接着“十倫之一——自立體”來講的。總之，我們可以知道，“幾何”這一“府”與邏輯學關係密切。利瑪竇不否認中國有數學研究、只是缺乏邏輯性強的原本之論：“竇自入中國竊見為幾何之學者，其人與書信自不乏，獨未讀有原本之論，既缺根基，遂難創造，即有斐然述作者，亦不能推明所以然之故，其是者己亦無從別白，有謬者人亦無從辯證。”

       我們現在是把《幾何原本》看作一本數學書的，與徐光啓同時代的人幾乎都沒有把幾何原本看作一本數學書，而是看作一本探求萬事萬物之理的邏輯方法書。徐光啓把它看做數學的根本而不是數學本身：“《幾何原本》者度數之宗，所以窮方圓平直之情，盡規矩準繩之用……蓋不用為用，眾用所基，真可謂萬象之形圉，百家之學海。”王徵在其著作中強調了鄧玉函（Terrentius）的觀點：“鄧（玉函）先生則曰：‘譯是不難，第此道雖屬力藝之小技，然必先考度數之學而後可。蓋凡器用之微，須先有度有數。因度而生測量，因數而生計算，因測量計算而有比例，因比例而後可以窮物之理，理得而後法可立。不曉測量、計算，則必不得比例；不得比例，則此器圖説必不能通曉。測量另有專書，算指具在同文，比例亦大都見《幾何原本》中。’”

2“幾何之學”相當於今天的數學

     “幾何之學”，在徐光啓、利瑪竇和當時的其他人看來，所對應的拉丁文是Mathematicarum。艾儒略的《西學凡》（1623年刊行）即採用這一用法：“幾何之學，名曰馬得馬第加者，譯言察幾何之道，則主乎審究形物之分限者也，復取斐祿之所論天地萬物，又進一番學問。……獨專究物形之度與數，度其完者為幾何大，數其截者以為幾何眾，……”。李之藻和傅汎際也是持這一看法：其“明藝之二”明確界定了今天所説的數學為“審形學，西言瑪得瑪第加，”所以“審形學”、“察幾何之道”、“幾何家”，才是“幾何之學”的同義詞。筆者對徐光啓和利瑪竇關於西方數學的著作進行了考察，在利瑪竇的表述，比如《譯﹤幾何原本﹥引》（對該文的作者學界也有不同看法，本文認為是利瑪竇）中比比皆是，但徐光啓關於《幾何原本》的論述，一般不單獨用“幾何”一詞，多數情況下，“幾何”和“原本”同時出現。

      上文也已經説明過，利瑪竇、艾儒略和李之藻、傅汎際等人均將幾何家稱為“量法家”，將“量法”作為Geomitria的漢譯。

參考文獻

宋芝業 《 “幾何”曾經不是幾何學——明末“幾何”及相關學科命名新探》，****《科學文化評論》第8卷第三期科學與人文

艾儒略 1978．《西學凡》．1623年刊行．見：李之藻輯刻．《天學初函》．台北：台灣學生書局．頁37-38．

安國風 2008．《歐幾里得在中國》．紀志剛等譯，南京：江蘇人民出版社．頁473．

白尚恕 2008．《中國數學史研究——白尚恕文集》．李仲來主編．北京：北京師範大學出版社．頁368．

杜瑞芝(主編) 2000．《數學史辭典》．濟南：山東教育出版社．頁407．

馮天瑜 2003．晚明西學譯詞的文化轉型意義．《武漢大學學報人文科學版》，**11:**567-674．

傅汎際譯義，李之藻達辭 1959．《名理探》．北京：三聯書店，1959．頁12．

梁宗巨1980，《世界數學史簡編》，遼寧人民出版社．頁90．

利瑪竇口授、徐光啓筆受 1939．《幾何原本》．北京：商務印書館．頁1．

梅榮照、王渝生、劉鈍 1990．歐幾里得《原本》的傳入和對我國明清數學的影響．見: 梅榮照主編，《明清數學史論文集》．南京: 江蘇教育出版社．頁53-83．

歐幾里得2003．《幾何原本》．蘭紀正等譯．西安: 陝西科學技術出版社．

孫宏安 2008．《中國古代數學思想》．大連：大連理工大學出版社．頁49-51．

徐光啓 1984．《徐光啓集》．上海：上海古籍出版社．頁59．

徐宗澤 2006．《明清間耶穌會士譯著提要》．上海：上海書店出版社．頁199．

亞里士多德 2003．《工具論》．餘紀元等譯．北京：中國人民大學出版社．頁5．

嚴敦傑 1959．幾何不是Geo的譯音．《數學通報》, (11): 31．

張柏春等 2008．《傳播與會通——﹤奇器圖説﹥的研究與校注（下篇）》．南京: 鳳凰出版傳媒集團/江蘇科學技術出版社．頁20．