格拉斯曼:擴展的學問與線之代數丨賢説八道_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2021-01-25 10:26
We need an analysis which is distinctly geometrical or linear, and which will express situation directly as algebra expresses magnitude directly. (1)
——Gottfried Wilhelm Leibniz
Thus pure mathematics is the theory of forms. (2)
——Hermann Günther Graβmann
1 疑 惑

2 奇異數學兩例
先説用代數證明幾何題。1679年,萊布尼茲暢想應有一種普適代數 (universal algebra),能直截了當地 (directly and simply) 處理幾何對象。這一點在歐幾里得的幾何裏其實已實踐過,只是我才剛學到,有點大驚小怪。考察三角形ABC底邊BC邊上的一點D,則三角形

歐幾里得的幾何有兩個元素,點和線 (段)。那麼三角形是啥?三角形由三個線段構成的閉合線所圍成的一塊麪積,它可以看作是由兩個共點的 (有取向的) 線段所決定的 (有取向的線段如今稱為simplices)。因此,這個三角形,有取向的,是由兩條有取向的線段通過某種積所決定的。三角形是linear product (線之積)的結果。AB=A’B’ ,兩線段長度相等,取向相同;ABC=A’B’C’ ,三角形形狀全同,取向相同。
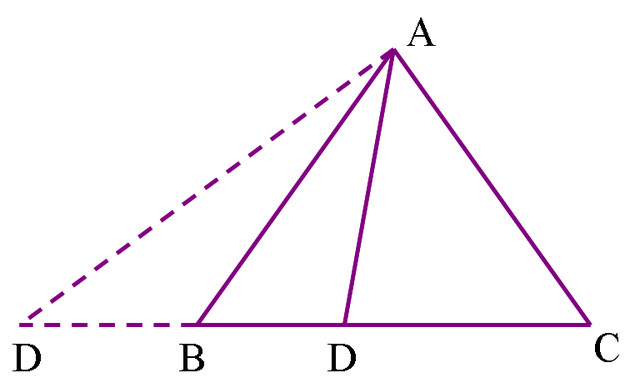
考察一條線段ABC,B在中間時,大家容易接受 AB+BC=AC 。可是,如果給線段以方向,則有 AB=-BA,那麼不管一條線上A、B、C三點是如何安排的,總有 AB+BC=AC 。可以移項,得 AB=AC-BC=AC+CB。對於AB=-BA ,把AB看作是A、B之間的一種乘積,具有性質 AB=-BA 的乘積就構成了一種新的代數,外代數 (exterior algebra) 。
用A, B…這樣的單個字母代表點,AB是A, B的積,有性質 AB=-BA 。由此得 ,A^2=0,A就是格拉斯曼數。引入實數 α+β=1 ,記P=αA+βB,則 AP=βAB,PB=αAB ,故有 AB=AP+PB,P是AB上的一個點 (這裏是數與點的乘積)。注意,兩個點之差是矢量 (the difference of two points is a vector),則 (A-B)+B=A 意思是矢量 (A-B) 以“+”這種操作把點B變成了A (你把這個操作解釋成挪動,那就是詮釋了)。
有了這套學問,幾何就好辦了。設A, B, C 是三角形三頂點,設D是AB邊上的一點, E是AC邊上的一點,且分別將兩邊長分成相同的比例。則有,D=(1-α)A+αB ,E=(1-α)A+αC ,兩式相減,得 D-E=α(B-C) 。啥意思?就是 D-E與 (B-C) 平行,長度比為 α 。D-E=α(B-C) 表示兩線段平行,多麼一目瞭然啊。再舉一例。證明平行四邊形的對角線平分之。對平行四邊形ABCD,有A-B=D-C, 移項得 A=D-C+B 。從右側接連乘上B, C,得 ABC=DBC。換一種移項方式,得 A-B+C=D ,從左側接連乘上B,A,得 ABC=ABD 。這樣 ABD=DBC。QED。整個證明過程就是用到代數的加減和乘法。有了這樣的代數幾何,幾何就是一道代數題 (別跟幾何代數弄混了。那個學問太難!)
有些的讀者可能注意到了,把乘法形式的 AB 和減法形式的 A-B 都當作矢量沒有矛盾,它們都滿足反交換的性質。還記得整數依據慣常的加法構成加法羣嗎?那個加法對於整數就有羣論意義下的乘法的功能。這只是記號問題。
再看如何解線性方程組。1853年,法國數學家柯西發表了一篇論代數鑰匙的論文 (Augustin Cauchy, sur les clefs algébriques, Comptes Rendus, 1853)。為簡單起見,以二元線性方程組為例,求解
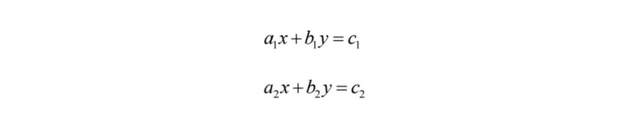

格拉斯曼 (Hermann Günther Grassmann,1809-1877) 是個德國多面型學者,著名的數學家、語言學家,對物理有深刻影響 (電動力學),職業上他是一位出版人 (圖2)。格拉斯曼1809年出生於離柏林不遠的Stettin小鎮 (今屬波蘭),幾乎畢生生活在那裏,其父為中學的數學、物理老師,但他顯然是具有開創能力的學問家。格拉斯曼小時候跟媽媽學音樂,彈鋼琴,但記憶力差也不專心。他爸認為這個十二個孩子中的老三沒啥天分。格拉斯曼自1827年起在柏林大學學習古典語言、哲學與文學三年。受歷史學家August Neander和Friedrich Schleiermacher的影響,大學期間格拉斯曼對數學發生了興趣,但沒有跡象表明他曾選修過數學或者物理的課程, 倒是讀過一些包括他父親撰寫的數學書和物理書。格拉斯曼1830年畢業後才算認真開始學習數學,同時攻讀數學、物理、博物學、神學和語言學,以便取得這方面的中學教師資格。1834年格拉斯曼曾接受柏林技校由數學家Jaco Steine留下的位置,因為後者到柏林大學任職去了。一説1834年開始格拉斯曼在柏林的奧托中學教數學,1847年獲得高級教師 (Oberlehrer) 的稱號,1852年在43歲上才在Stettin中學接替了其父的位置,獲得了Professor 稱號 (Professor來自動詞profess, 在法語、德語裏professor也用於中學老師。確切譯法是講述者、授課者)。格拉斯曼沒有在大學獲得教職的經歷,1847年他曾寫信給普魯士教育部想弄個大學教職,但沒成功。然而,格拉斯曼隻手創立了一個新的數學體系 (外代數),其意義可和創造非歐幾何與布爾代數相比擬。他的經典著作,《擴展的學問》1844版和《擴展的學問》1862版,一直未為同時代的數學家所認可,但今天卻是諸多數學分支和數學物理的基礎。初讀格拉斯曼,你會懷疑你曾學過歐幾里得幾何和線性代數。問題的真相是,我學過甚至教過,但是確實跟沒學過一樣!此外,他還是個成功的語言學家,比較語言學學者,東方學學者,格拉斯曼翻譯的《梨俱吠陀》(Rig Veda) 及長篇評論,據大英百科全書,至今仍被研究使用。

4 格拉斯曼學問的緣起
從畢達哥拉斯到十九世紀中葉,幾何學的基本問題都是如何將數賦予幾何,這對域論和線性代數的創立至關重要。實數的概念由荷蘭人史蒂文 (Simon Stevin, 1548-1620) 於1600年完成,實數納入幾何則始於笛卡爾和費馬於1630年代的工作。給幾何對象賦予數值非常笨拙,為此選擇的原點與座標軸不是問題本身必須的。1679年,萊布尼茲提及了建立普適代數 (universal algebra) 的可能性,可以directly and simply 處理幾何對象。萊布尼茲設想的普適代數,是想發現用計算研究圖形性質的方法 (系統) ,希望能用於處理力學。
格拉斯曼的父親老格拉斯曼 (Justus Günther Grassmann),一位中學數學老師,也是個幾何大家,可説是空間的理論 (Raumlehre) 開創者。老格拉斯曼的幾何積 (geometric product) 的概念同複數的幾何表示傳統或者“力的平行四邊形”傳統之間有聯繫。老格拉斯曼注意到意大利數學家韋達 (François Viète, 1540-1603) 的新代數強調 “le rectangle est réellement le vrai produit de deux longueurs (直角形(矩形)本質上是兩個長度真正的積) 。” 筆者覺得可不嘛,你看那乘號× ,就是直角啊。在代數方程中,我們就是把 xx=x2 稱為“x squared”的。平行四邊形同正方形沒有本質的不同,它也應該是線段的某種積的結果,而正方形只是特例。當然了,共線是另一個極限的情形。這引出了外積的概念。老格拉斯曼的學問和著作,為格拉斯曼提供了思想啓蒙。
據格拉斯曼自己的信件,他在1832年即考慮兩條或者多條線的幾何和 (差) 與幾何積的問題。格拉斯曼讓他的一開始沒有內容的形式取各種值:數,點,矢量,有取向的面、體,等等。他甚至提出了16種不同的乘法 (連接)。格拉斯曼發現他的學問緣起於幾何,但是幾何只是特殊應用。他的學問是以純粹抽象的方式得到了和幾何相似的規律。打破了三維空間的限制是其優點之一。1839年格拉斯曼把這個學問弄成了可以應用到所有力學問題的程度。為了證實自己的實力,格拉斯曼於當年撰寫了Theorie der Ebbe und Flut (潮汐的理論) 一書。此書格拉斯曼雖然多次提到,但是遲至1911年才得以出版。1840年,格拉斯曼寫過一篇論述如何用他自1832年就開始琢磨的矢量方法來表述拉普拉斯的天體力學和拉格朗日的分析力學這兩部經典。因為發現了新的應用與擴展,加上同時忙於許多事務,格拉斯曼於1842年才開始撰寫著作闡述自己的擴展的學問,1844年出版。萊布尼茲當初期望的納入實數的幾何,由格拉斯曼幾乎憑一己之力創造出來了。1861年格拉斯曼重新從公理化的角度定義了加法與乘法,以及這些運算的結合律、交換律、分配律,這比Giuseppe Peano (1858-1932) 和 Georg Cantor (1845-1918) 早了二十多年。有一種説法Möbius, Bellavitis, Hamilton, Grassmann, Saint-Venant和Cauchy 等人都幾乎獨立地考慮過相似的思想。研究動機來自幾何,但亮點主要是代數的。格拉斯曼關於點的學問、點的分析也被莫比烏斯 (August Ferdinand Möbius, 1790-1868) 獨立發現,並被用不同的方式所發展和表達過。
也許引用格拉斯曼自己的表述是恰當的。“第一個衝動來自對幾何中的負數(量)的考慮。我已習慣了把距離AB和BA看作是相反的量。AB+BC=AC ,當A,B,C不在一條線也依然成立。當我探討幾何積的這個概念的時候,這個概念已經由家父建立 (見於Raumlehre, part I, p.174 (一説是part II, p.194), Trigonometrie, p.10),結論是不僅是正方形,而是平行四邊形,也可以看作相鄰兩邊的積;假設邊可看作是有方向的量。轉動的概念導致幾何指數量 (geometrical exponential magnitudes), 以及導致三角函數的分析。”
格拉斯曼把他的學問稱為《擴展的學問》,筆者甚為歎服。數學,還有物理的發展一直在表現擴展的過程。這個擴展,是空間的擴展,對象的擴展,體系的擴展。僅僅從直線段上的 AB+BC=AC ,他就想到不共線時也應該成立,就是一種擴展。若 x+y=c 裏都是數或者量 (numbers or magnitude),這就是關於數或者量的代數。在 (A-B)+B=A 中, A表示點, (A-B) 表示矢量,這就是表示幾何的代數。這也是一種擴展。克利福德後來將加法擴


格拉斯曼引入了外積的概念。先是點的外積。AB=A-B 是從點B到點A的一個矢量 (not a vector from A to B, but as a vector limited to positions in the line through A and B, that’s line-bound vector! 矢量, vector, 是哈密頓為了他的四元數在同時期引進的一個詞兒),但是因為有AA=0 ,AB=-BA ,顯然這個 AB=A-B 就是外積。接着是矢量的外積。對於任意多個矢量,外積為0意味着它們必是相關的。格拉斯曼指出,外積的特徵是有如下性質:兩個相關的量,其外積為0。當然了這個性質不是積的必然性質,還可以定義別的積。

可以從共點的兩線段從重合時將其一逐漸打開張成一個平行四邊形的過程來看外積和內積。外積對應所張的有取向的平行四邊形的面積,為交換反對稱的,過程開始時對應的外積為0。然而面積並不能完全確定這個平行四邊形。內積為兩線段之一與另一者在其上投影的乘積,過程開始時應取極大值,為交換對稱的。內積為0是兩線段 (矢量) 垂直的判據;外積為0是兩線段 (矢量) 平行的判據。
5.3 關於矩陣本徵值問題

格拉斯曼構造的是一個全新的數學體系。他發現那不是幾何,而是一門新的科學,幾何只是一個應用領域而已。格拉斯曼嘗試過多種不同的表現形式,最終於1844年出版了《擴展的學問》 (圖3)。無疑地這是一本經典(請記住作者是語言學家),但是格拉斯曼要做的是發展一個寬大的新體系,而且思想還不好提取出來 (新思想的表達需要新概念、新語言體系以及新的表達方式),為此該書開始還有哲學的鋪墊,故而這本書雖然思想內容豐富,但可讀性值得商榷。這本書當時印了多少冊已無可考,但顯然鮮有人問津。1844版的出版人在1876年給格拉斯曼的信寫道:“您的著作Ausdehnungslehre無存貨已有一段時間了。因為您的大作幾乎無人問津,大約有600本在1864年被當成廢紙用了,剩下的那麼幾本最近賣出去了,我們的書庫裏還有一本。”
格拉斯曼本人一直在嘗試為自己的學問找到恰當的表述方式,其《擴展的學問》1862不是1844年版的重印,而是重寫。令人惋惜的是刪掉了此前的哲學闡述。所謂的《擴展的學問》1862,應該在1861年就有了,在那年10月格拉斯曼就送了一本給莫比烏斯,不過有300本上印着的日期是1862. 《擴展的學問》1862全名為Ausdehnungslehre:vollständig und in strenger Form bearbeitet (擴展的學問—以完備、嚴謹的形式呈現的),不過迎來的還是失望,甚至比第一本書更少受到關注。《擴展的學問》1844的第二版於1878年刊出,那時格拉斯曼已經去世了。《擴展的學問》1844和《擴展的學問》1862可作為兩本書看待。

7 格拉斯曼理論的接受問題
用後世的眼光來看,格拉斯曼是幾何計算、外代數、矢量空間理論的奠基人。作為一個知道自己做出了偉大成就的中學老師,他想獲得當世數學家認可的心情估計是強烈的。然而,如同阿貝爾,伽羅華,康託一樣,格拉斯曼是那種十九世紀不幸的偉大數學家,直到其辭世的1877年,格拉斯曼的數學所獲得的認可幾乎是聊勝於無。有一種説法是,格拉斯曼遭遇的是非同尋常的忽視 (colossal neglect)。
格拉斯曼的《擴展的學問》1844幾乎沒受到什麼關注。他肯定是送了一本給高斯的,高斯在1844年12月14日答覆道:“我曾在半個世紀前考慮過相關問題,並於1831年就發表過一些結果。”高斯指的可能是他在複數的幾何表示方面的工作。大數學家莫比烏斯應該是對格拉斯曼很早就有所耳聞,1839年,他評價格拉斯曼的晶體學工作很有意思。當然,晶體學首先就是關於空間堆垛的問題,而空間學是格拉斯曼父子考慮的主題。格拉斯曼1644年送了莫比烏斯他的《擴展的學問》,莫比烏斯也是作了評論的:“對於格拉斯曼著作中作為數學元素基礎的哲學元素我無意用正確的方式予以讚賞,甚至不能正確理解。”莫比烏斯認為格拉斯曼的著作缺少直觀性 (intuition, Anschaulichkeit) 這個數學思想的基本特徵, 他不得不跳過那些格拉斯曼稱為extension或者generality的東西。其實,愚以為,extension and generality (擴展與一般性),這後來都成了數學的傳統了, 什麼東西都有個generalized 版本,連相對論都未能逃脱這個命運。這恰是格拉斯曼偉大的地方啊。有能力處理一般性和抽象,才是大科學家!
1846年,莫比烏斯邀請格拉斯曼參加一場數學競賽,解決一個由萊布尼茲提出的問題:發明一種不用座標和度規性質的幾何算符 (萊布尼茲稱為analysis situs, 即是後來的拓撲學) 。這個思想,不正是後來廣義相對論要呈現的思想嘛!格拉斯曼以一篇Geometrische Analyse geknüpft an die von Leibniz erfundene geometrische Charakteristik (同萊布尼茲所發明的幾何特徵相聯繫的幾何分析)勝出,但被莫比烏斯批評其使用了抽象符號而未對讀者交代為什麼這些符號是有價值的。格拉斯曼雖然憑這篇勝出 (好像是為他量身定做的,只有他一份答案),但沒對他的命運帶來改變。
就幾何代數而言,有三個人是必須提到的,格拉斯曼、愛爾蘭的哈密頓與英國的克利福德。哈密頓在1843年發明了四元數。格拉斯曼思考空間的學問,把幾何當作代數;哈密頓考慮時間,把時間作為純粹的代數 (pure algebra),不知時空的概念是不是也能產生什麼新穎的代數。哈密頓得到一本《擴展的學問》1844版,覺得不好懂,他曾寫信給August de Morgan (1806-1871),説為了能讀格拉斯曼他可能不得不學抽煙。1852年哈密頓讀格拉斯曼的書,一些評論發表在他的Lectures on quaternions (1853) 的序言中了。哈密頓認為這是可以和他的與四元數相關的工作相提並論的成就,現在是讀起來with admiration and interest. 這應該算是對格拉斯曼學問的認可,可能是由於那個時代交流不便,這個1835年30歲上就封爵的愛爾蘭數理大神的認可沒能對格拉斯曼及其學問的命運產生及時的影響。
格拉斯曼的《擴展的學問》是他生命的傾情奉獻。到了1861年,格拉斯曼對他的成就所遭到的冷遇是有點憤懣的。格拉斯曼在他的《擴展的學問》1862版序言中寫道 (大意) :“我堅信就算再過17年甚至更長的時間這本書無人問津,不能進入科學的正軌,有一天它也會從遺忘的塵埃中被發現,如今沉睡的思想終會開花結果。……因為真理是永恆的、神聖的(Denn die Wahrheit ist ewig, ist göttlich……),真理的任何發育階段都不會不留痕跡。”
在盛產數學家的德國及周邊地區,格拉斯曼所創立的學問要説無人識貨,這也不正常。其實,1860年意大利的Cremona, Bellavitis 和 Peano等人對格拉斯曼的著作就產生了興趣。1866年德國青年漢克爾 (Hermann Hankel, 1839-1873) 來信讚揚格拉斯曼的闡述,並要求其能進一步整理,這算是對格拉斯曼的承認,但那時漢克爾不夠分量。1869年,克萊因 (Felix Klein, 1849-1925) 注意到了漢克爾Vorlesungen über die complexen Zahlen und ihre Functionen (複數與複函數教程) 一書中提到了格拉斯曼的名字。克萊因向克萊布什 (Alfred Clebsch, 1833-1872) 推薦了格拉斯曼,還跟Sophus Lie提及格拉斯曼的工作。後來,克萊因坦誠深受格拉斯曼的影響,甚至影響了他1872年的埃爾朗恩綱領。1871年,經由克萊布什推薦,格拉斯曼入選了哥廷恩科學院的通訊成員。至此,格拉斯曼算是得到了認可,不過格拉斯曼在1877年就過世了。1878年克利福德出版了“格拉斯曼展開代數的應用” (une Application de l’algèbre de l’extension de Grassmann ??),美國留學生吉布斯和克萊因一起在1894-1911年間整理了格拉斯曼的著作。到了1870年代中期,在英國也有Hermann Noth (1840-1882)、William Kindgdon Clifford (1845-1879)、W. Preyer (1841-1897)等人對格拉斯曼的工作產生興趣。注意這些數學家大多在50歲前就去世了。這些數學家,如同北極冰雪下的植物,在極短的生命裏早早地開出極為燦爛的花朵,結出可以連接下一個春天的果實!
1878年,格拉斯曼的《擴展的學問》1844版的第二版出版。格拉斯曼在序言中提到黎曼的學生漢克爾在1867年論述複數體系的理論 (Theorie der complexen zahlensysteme) 時強調了其學説的重要意義,1/10的內容用於介紹格拉斯曼的工作。這説明,格拉斯曼臨終歲月裏是知道自己的著作已經被人接受了的,這些多少對格拉斯曼是個安慰。
格拉斯曼之成就與著作的未被認可,反映在其人的境遇上。雖然幾經嘗試,但終其一生,格拉斯曼都未能在大學謀到一個教數學的差事。發現格拉斯曼價值的漢克爾和克萊布什不久年紀輕輕就辭世了;德國的莫比烏斯、英國的哈密頓和意大利的Bellavitis 夠分量,但在別處有要提倡和擁護的東西;而熱心腸的Victor Schlegel (1843-1905) 人微言輕,熱情超過能力。其實,這種革命性的發現被忽視,歷史上早有先例,這也不是例外。然而,正如格拉斯曼所堅信的那樣,真理是永恆的。今天的數學物理領域,格拉斯曼所創立的數學是其中燦爛的瑰寶,格拉斯曼的學問會為有心數學與物理的人們提供源源不盡的靈感。
8 多餘的話
研究格拉斯曼讓我對線性代數這個全世界理工科人都要學習的科目有了新的認識。2020年12月19日我認識到所謂的線性代數是對lineale Algebra (linear algebra) 的錯誤翻譯,正確的翻譯是“線之代數”,即人家本意的algebra about line segment,一時間悵然若失。這個學問來自數與點、數與線乘積的擴展。就着錯誤的概念學習,不明白一門學問的緣起,耽誤了多少人的寶貴時光。想起了那句《西遊記》的名言,“不聞至人傳妙訣,空教口困舌頭幹!” 學問是講究傳承的,這一點不服不行。
我們小時候學過一點淺淺的幾何與代數,淺得連基本的經典力學入門都不夠用,殊不知幾何、代數本是一體的。不能分析幾何的代數不是真正的代數,and vice verse。格拉斯曼、哈密頓和克利福德奠立的幾何代數,是能用於幾何的代數學;與此相對,代數幾何 (algebraic geometry) 則利用抽象代數技術研究多變量多項式的零點集合的幾何問題。你眼裏是看到代數還是幾何,是幾何代數還是代數幾何,還是個渾然一體,全在於你自己。格拉斯曼的代數更適於物理,因為它區分矢量與贗矢量。對矢量和贗矢量不加區分,讓電磁學理論始終是一團糊塗醬。用矢量導數及逆矢量導數表示的麥克斯韋方程組不妨瞭解一下。

格拉斯曼博學、高產。除了重點介紹的《擴展的學問》和《梨俱吠陀》譯本,1844-1861年間格拉斯曼發表了17篇包括物理學的科學文章,還有一些數學和語言的課本,包括1861年的Lehrbuch der Arithmetik (算術教程)。哦,為了評價格拉斯曼的高產,有必要順帶提一句:格拉斯曼於1849年結婚,除了產生了那麼多的思想成就以外,還連生了11個孩子。這一點,他也是繼承了其父的優點,他是12個孩子中的老三。格拉斯曼繼承了父親的數學思想,成為一個數學領域的開創者,但終生未能謀到一個大學教職;後來他的一個兒子 (Hermann Ernst Grassmann) 成了數學教授,算是圓了他的夢想。
注:本文改寫自曹則賢著《磅礴為一》一書。
參考文獻
[1] Michael J. Crowe, A history of vector analysis, Dover Publications, Inc. (1967).
[2] Vincent Pavan, Exterior Algebras: Elementary tribute to Grassmann’s ideas, ISTE (2017).
[3] Alfred North Whitehead, A treatise on universal algebra with applications, Cambridge (1898).
[4] Hermann Günther Grassmann, Gesammelte mathematische und physikalische Werke (數學物理全集), 3 Bde., Friedrich Engel (ed.), Teubner (1894–1911).
[5] Hermann Günther Grassmann, Geometrische Analyse geknüpft an die von Leibniz erfundene geometrische Charakteristik, (1847).
[6] Hermann Günther Grassmann, Die lineale Ausdehnungslehre, ein neuer Zweig der Mathematik, Wiegand (1844). English translation by Lloyd Kannenberg, The linear extension theory: A new branch of mathematics, Open Court (1995).
[7] Hermann Günther Grassmann, Die Ausdehnungslehre. Vollständig und in strenger Form begründet, Enslin (1862). English translation by Lloyd Kannenberg, Extension Theory, American Mathematical Society (2000).
[8] Hans-Joachim Petsche, Gottfried Keßler, Lloyd Kannenberg, Jolanta Liskowacka (eds.), Hermann Graßmann Roots and Traces: Autographs and Unknown Documents, Birkhäuser (2009).
[9] August Ferdinand Möbius, Der barycentrische Calcul, Leipzig (1827).A. Fraenkel, Über die Teiler der Null und die Zerlegung von Ringen, J. Reine Angew. Math., 145, 139-176(1915).
[10] Henry George Forder, The calculus of extension, Cambridge (1941).
[11] Otto F. Fischer, Universal Mechanics and Hamilton’s Quaternions, A Cavalcade (Stockholm, 1951).
[12] Otto F. Fischer, Five Mathematical Structural Models in Natural Philosophy with Technical Physical Quaternions (Stockholm, 1957).
註釋
(1)我們需要一門分明是幾何的或者是關於線的分析,其如同代數直接表達量一樣直接表達位—萊布尼茲。這句裏的situation [situs]不好翻譯,是關於位置、形有關的概念, 可在geometry of situation 的語境中加以理解。龐加萊1895年發表的Analysius situs成了後來的拓撲學(topology)。
(2)純數學是形式的理論——格拉斯曼
(3)AB=-BA, 走過路的都懂這個道理。距離也是有方向的量。不過,你敢認為AB是A和B的一種乘法嗎?
