無法割捨——幾何代數視角下的功與力矩丨賢説八道_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2021-02-17 12:41
力做功,力還產生力矩,但是力是怎麼分清楚這兩份工作的?如果力自己都做不到,那我該怎麼辦?我上初中時就覺得這地方有點兒不對勁,但是我們的中學、大學、研究生的物理課本對此問題都視而不見。其實,當力矢量 F 遇上位移矢量 dx 的時候,那個乘法 Fdx 天然地就是幾何積,而這樣的學問是1870年代就有了的。我們的中學生都能明白,只是沒有人教。
**撰文 ****|******曹則賢(中國科學院物理研究所)
I am not and grieve not.
——克利福德的墓誌銘
1 疑 惑
我初中二年級時開始有了物理課,從力學 (theory of force) 入手,往後在大學到研究生階段又學了各種力學 (mechanics),以及一些動力學 (dynamics) 的理論。這麼説吧,力估計是人們學物理結識的第一個對象。力的概念來自一種生理學的感知,提、拉、拽、扔都會讓手臂有緊張感,你就感覺到力的存在了。力,被當作一個重要的物理因素率先進入人類的認知活動。亞里士多德説力是造成運動的原因,你不費力拉車,那車子就不動彈。伽利略説不對,一個物體沒有外力它能一直保持原來的狀態,照樣往前運動,力是運動被改變的原因。牛頓説再具體一點兒吧,讓力與速度被改變的劇烈程度,即加速度,成正比


然而,對於天平、桿秤來説,平衡是測度為零的事件,是例外而非常態,更多的時候體系會被弄得圍繞着支點轉了起來。那麼,這個一般情況下施壓加一個力所產生的、與平衡或者轉動有關的物理效應該怎麼描述呢?為此,教科書裏突然就冒出來了力矩的概念,M=r×F ,並且強調 r 是參照點到着力點的空間矢量,× 這個乘法與 2×3.14=6.28 中的算術積不同了,叫叉乘 (cross product),乘出來的這個結果,力矩M,也是矢量,並且按照 r→F→M 的順序構成右手定則。有許多高中、大學的教科書在那裏努力闡述如何使用右手定則,卻不去問這叉乘是個什麼乘法、哪兒來的啊?又,r→F→M 構成右手定則,不對啊,在平面裏可沒有什麼右手定則,力加到恰當的地方一樣引起轉動啊?

圖1. 天平與桿秤

乘法被稱為標量積,有些地方又叫點乘、內積 (這兒有點亂)。這下子,問題好像清楚了:“力矢量和位移矢量之間有兩種乘積,點乘和叉乘,點乘同做功有關,而叉乘同力矩有關。用哪個,看你考慮什麼問題。” 可是,不對啊,力怎麼知道什麼情況下做功什麼情況下產生力矩 (圖2),什麼情況下該點乘什麼情況下該差乘啊?這個問題讓我從中學起一直很困惑。讓我更困惑的是,那些大學教科書給我的印象是編者們一點兒都不困惑,這讓我很自卑。我一直小心翼翼地把這個困惑藏在心裏。我教過某些大學本科的力學輔導課,給某大學力學教研室的教授們講過如何講經典力學,但我也忍着不提這茬兒。昨天,我忍不住了。

圖2. 這推的人是在做功呢還是在產生力矩呢?
其實,相關的內容,嚴謹的內容、成體系的內容,在1840年代就初步成型了。到了1878年,Applications of Grassmann’s extensive algebra 一文橫空出世,類似力與位移矢量乘法的問題不僅沒有了身份不同的問題,沒了空間維度的限制,還有了除法!要是學會了的話,接下來去學經典力學、電動力學、量子力學、相對論和規範場論還感覺暢通無阻呢。意外不?
2 外積、內積與標量積、矢量積與點乘、叉乘
外積、內積的概念來自德國中學老師格拉斯曼 (Hermann Graßmann, 1809-1877),一開始是關於線段之間的乘積。設想正方形是由兩條線段張開的,面積等於 S=aa 。若把思想擴展一下,線段是有取向的,而平行四邊形也是由兩個線段張開的,這兩個有方向的線段的乘積不就決定了這個平行四邊形的面積和取向?於是,格拉斯曼定義了兩矢量的外積(exterior product, outer product),a∧b ,這個乘法滿足反對稱性,a∧b=-b∧a ,其結果是個二矢量 (bivector),比矢量高一個層次, 可從幾何上理解為面是比線高一個層次的存在。然而面積與取向並不能完全確定這個平行四邊形。格拉斯曼還注意到,當一個線段從另一個共點的線段上出發,掃過一個角度去張開一個平行四邊形時,它在另一個線段上的投影也一直在變——從出發處的整個長度變為相互垂直時的0。這個投影與投影在其上的線段之積顯然是一種新的積,一種對稱的乘積(interior product, inner product), a·b=b·a (圖3)。外積出現於內積之前。
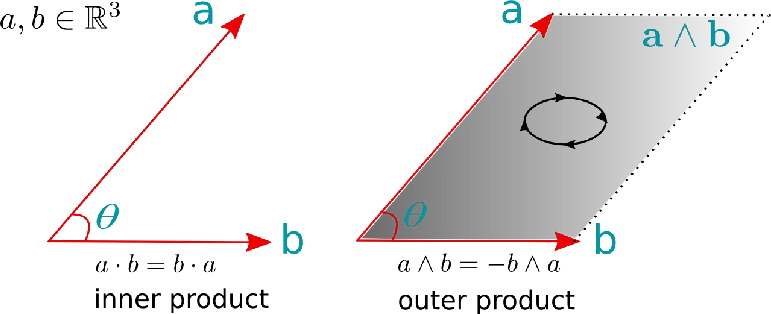
圖3. 量矢量的內積與外積
可以從共點的兩線段從重合時將其一逐漸打開張成一個平行四邊形的過程來看外積和內積。外積對應所張的有取向的平行四邊形的面積,為交換反對稱的,過程開始時對應的外積為0。內積為兩線段之一與另一者在其上投影的乘積,過程開始時應取極大值,為交換對稱的。內積為0是兩線段 (矢量) 垂直的判據;外積為0是兩線段 (矢量) 平行的判據。
當然了,有了矢量和矢量的外積,可以構造任意的多矢量 (multivector),對它們可定義內積、外積、遞歸積,還可以求補,等等。這套算法適應任意維的矢量空間。這是把思想從三維空間拓展到任意空間,把算法從簡單的算術乘法拓展到各種幾何乘積的結果,所以格拉斯曼把他的學問稱為Ausdehnungslehre (擴展的學問),第一本書於1844年出版。不過,結局是直到格拉斯曼去世,該門-學問幾乎無人喝彩。格拉斯曼後來憤而把時間專注於語言學研究。

Gibbs,1839–1903) 他們生生地把兩 (三維) 矢量的標量積和矢量積給割裂成了兩個獨立的乘積,標量積也叫點乘 (dot product),而哈密頓的矢量積去掉前面的負號變成了叉乘(cross product)。點乘和叉乘後來佔據了物理教科書,這種把一個數學整體的兩個部分當成獨立的兩個內容的作法,極大地傷害了物理學的表述。點乘、叉乘以及基於其上的矢量分析,按法國著名數學家丟多奈 (Jean Dieudonné, 1906–1992) 的説法,是那些毫無靈性的爛文人拿格拉斯曼和哈密頓的思想胡編亂造的 (which uninspired lacks concocted out his and Hamilton’s ideas)。丟多奈作為純粹數學家對數學不嚴謹的矢量分析的厭惡之情溢於言表。
1878年,英國數學家克利福德將格拉斯曼的外代數和哈密度的四元數代數結合到一起,創立了幾何代數 (geometric algebra)。在幾何代數中,兩個矢量的幾何積定義為 ab=a·b+a∧b,其中 a·b 是格拉斯曼的內積, a∧b 是格拉斯曼的外積, 類似哈密頓的四元數乘法包含標量積和矢量積。但是,克利福德代數克服了四元數代數只適用於三維矢量空間的侷限以及其中的一些錯誤認識,它適用於任意維空間,有除法。更重要的是,它發展了格拉斯曼的擴展的學問,對應任意n維矢量空間的克利福德代數是 2n-維的代數,而且具有強大的計算能力、緊緻的表達能力。用它學習經典力學、電動力學、量子力學、相對論和規範場論,讓人少了很多迷惑,推導的過程也簡化許多。
而那個讓我從中學時就疑惑不解的力到底是做功還是產生力矩的問題,也迎刃而解。當力矢量 F 和位移矢量 dx 相遇時,它們的積從一開始就天然地是幾何積,Fdx=F·dx+F∧dx ,其中的內積項 F·dx 就是做功,而外積項 F∧dx 就和力矩有關(和 M=dx×F 之間還差個單位贗標量。感興趣的讀者請自行修習相關內容)。這兩者,做功與產生力矩,不可割裂!
3 多餘的話
作為一個當了25年學生和21年教授的人,關於教科書、教師以及學問,我多少有一些感慨。因為怕得罪人,也一直懶得説出來;可我又希望我們一代一代的少年別這麼一直被耽誤下去,所以忍不住還想説。那就少説兩句吧。我覺得吧,作為教師,好學的姿態和不停地學的實踐是起碼的任職資格。作為一個教師,我想因為我的一直不學無術,我只欠世界半個道歉,而我若一直固步自封,那我就欠世界一個半道歉,畢竟不學無術可能事關天資不足,是可以自我原諒的,而固步自封那就純屬是思想問題了。

圖4. 英國通才型學者克利福德
介紹幾句克利福德吧,為了致敬。克利福德 (William Kingdon Clifford, 1845-1879),一位物理學家+數學家+哲學家+作家型的通才 (polymath), 一個路過人世僅僅34年的天才 (圖4)。克利福德15歲考上倫敦國王學院和劍橋三一學院,26歲獲聘數學與力學教授,29歲當選英國皇家學會會士。他在格拉斯曼 (Hermann Graßmann, 1809-1877) 之擴展的學問 (Ausdehnungslehre. 格拉斯曼在其中曾提出16種乘法) 基礎上建立起了幾何代數,即以他的姓名命名的克利福德代數。本文介紹的關於幾何積的系統學問,源於他1878年發表的論文 (Applications of Grassmann’s extensive algebra, American Journal of Mathematics 1(4), 350–358(1878))。克利福德是頂級的物理學家,他的《動力學原本》光看副標題就足以理解動力學的內涵。那個讓愛因斯坦變得偉大的“引力是時空幾何的表現”之思想也來自克利福德,他於1876年在“on the space-theory of matter”一文中已確立了廣義相對論的主導思想。他在哲學論述中提出的mind-stuff (思維原料) 這一概念,可能震撼過很多人。人啊,長了個腦殼,最好抽空往裏面也塞點兒mind-stuff.
順便説一句,克利福德1875年結婚,婚後有兩個孩子,他為孩子寫了童話集 “the little people”。克利福德是為數不多的被自己的天才累垮了的人。
克利福德的墓碑上刻着:“I was not, and was conceived. I loved and did a little work. I am not and grieve not.”讀來太過心酸,我就不翻譯了。