瞧!這些發明算法的人_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2021-05-10 11:08
量子蒙卡
穿破青春未展顏
時光將老亦無閒
扯來量子縫裁好
披上清雲越景山
撰文 | 嚴正、孟子楊
1 編 按
物理學領域千年來發展至今,給人的印象大多是嚴謹、規範、自律和低調。文采飛揚、充滿感性、甚至於揮斥方遒及指點江山的物理人並不是那麼多。不多不代表沒有,即便是近現代,我們也能夠如數家珍一般舉出很多例子。歷史也誕生了很多通俗易懂、朗朗上口的名句,如“more is different”、“there’s plenty of room at the bottom”,起到了引領科學時尚的旗幟作用。
我國物理人中,亦有一些“文采飛揚、情懷感性”之前輩和當代佼佼者,自然不必提及“筆下娟秀、娓娓道來”的中國物理驕傲之楊振寧先生。當代人中,有如網紅物理人“賢説八道”的曹則賢。這裏還有一位,即本文作者之一的孟子楊。子楊老師行文通透、情懷充盈,卻一直從事着“極為嚴謹的”量子多體算法之類的研究工作。他似乎能夠在兩個能量簡併、但功能迥異的量子態之間隨意躍遷、收放自如。當然,他麾下有一位助手,即本文另一位作者的嚴正博士,也有類似氣質。
期刊《npj Quantum Materials》有幸得嚴正博士和子楊老師眷顧,而微信公眾號《量子材料》亦有緣刊登此文。
1 引 子
發明量子多體問題算法的人,多與普通人不同。他們身上有一種得道高僧、終南隱士的先知之氣,往往想要揚棄和重新評價流俗所看重的種種價值觀念,率性而為以至於不被社會所理解,甚至被視為狂士和瘋子。這其中的原因,恐怕還是來自於在量子多體問題中發明算法本身的難度。
對於量子多體物理學中的基本晶格模型,從量子 Ising 模型,到海森堡模型,到 t - J 模型、Hubbard 模型、量子 dimer 模型、及至時下流行的 K – Γ 模型、Yukawa – SYK、 Kang – Vafek 模型等等。這些問題的計算複雜度,在普遍情況下,都是隨着模型中自由度數目 (比如晶格中的電子數、自旋數、軌道數等) 而指數增加。物理學家想要從統計的意義上計算 100 個電子的物理性質,問題的相空間大小就是 2^100 或者 4^100 這樣的天文數字。而眼下,就算用到最快的超級計算機,人類的計算能力也只能進行代數複雜度的計算,更不要説處理實際量子材料中阿伏伽德羅常數 (10^23 ) 量級的電子了。
如此困難和挑戰,庶幾“人生有何意義”和“與爾同消萬古愁”這樣的終極問題,在一般意義上難有普適的答案。每天面對着這樣終極問題的人,其心態自然和普通人不同。這就好比古希臘的悲劇作家,他們明明知道命運是無法抗拒的,作為個人只能退而求其次,嘗試着用手中的筆誠惶誠恐地描述悲劇性抗拒的過程,以求得到精神上的出路和慰藉。
在這樣的背景之下,如果有人可以設計出一種合適的算法,成功地用代數計算複雜度去克服某個或者某一類量子多體晶格模型問題的指數相空間,其重要性就可想而知、其神奇更是讓人驚歎。從算法的發明人來説,因為看穿極度複雜問題的“曾經滄海”和“除卻巫山”,因為可以成功地克服看似不可能完成的任務而暫時地擺脱困擾人類的終極問題,他們自然就不願再被日常中柴米油鹽雞零狗碎的問題所牽絆。因此,他們也就漸漸開始揚棄流俗,獨自向着狂士和瘋子的方向前進了。阿門!
這樣的例子其實不少。比如提出了 h – index 的 Jorge Hirsch,他在量子多體研究方面很大的一項貢獻,即是完善了費米子行列式的蒙特卡洛 (determinant quantum Monte Carlo, DQMC) 算法。他在 1980 年代初期的工作,結結實實地告訴人們:半滿正方晶格 Hubbard 模型的基態是具有長程反鐵磁序的絕緣相。這些堅實的數值結果,為後來的 resonance valence bond (RVB) 圖像、doped Mott insulator 和 slave particle 描述自旋-電荷分離等等理論構想,打下了堅實基礎。而 Hirsch 本人,從此之後就不屑於凝聚態物理學當下那些一地雞毛般的雜碎問題了,開始向着狂士邁進,比如他老先生最近的文章:
J. E. Hirsch, Superconductivity, what the H? The emperor has no clothes, https://arxiv.org/abs/2001.09496, also in “APS Forum on Physics and Society Newsletter, January 2020, p. 4-9”.
這題目,就有一股查拉圖斯特拉那種“上帝已死”的尼采氣撲面而來。
再比如發明瞭解決海森堡等自旋模型的隨機級數展開 (stochastic series expansion, SSE) 算法的 Anders Sandvik。眾所周知,諸如海森堡模型或 XXZ 模型所描述的量子磁體基態、相變和動力學,都是老大難問題。但是,因為有了 Anders Sandvik 的 SSE 算法,從 1990 年代開始,人們便有了可以嚴格計算的高效手段。這一手段易學好用,已經變成眼下許多量子多體計算課題組入門學生的第一步學習資料。Sandvik 有個很有意思的中文名 —— 善德偉。此名雖然不及王重陽、丘處機這樣的名號高渺,但還是有一股道系仙氣和出世氣,都是我們芸芸眾生和普通羣眾所不能比擬的。
如此看來,在量子多體晶格模型中,還是有一些可以用代數計算複雜度來克服指數相空間的成功案例。縱然這些問題需要一個一個地克服,縱然在克服的過程中造就了諸位狂士和仙人,但重要的是,這些成功的算法,比如上面提到的 DQMC 和 SSE,不僅解決了問題,其核心在於在設計中抓住了問題的物理實質,讓我等豁然開朗。這些方法,不能只靠強大計算資源和高超編程技巧來解決問題,而更重要的是要運用物理學的原理來達到高效遍歷相空間的目的。事實上,高瞄如善德偉老師者,至今還對面向對象編程的做法嗤之以鼻。可見從業人員真正需要的,是追求技術和思想的共同進步,而不是頭痛醫頭、腳痛醫腳。量子多體前沿的物理人面對的現狀是:不能解決的問題遠遠多於已經解決的問題,所以每一步推進都顯得彌足珍貴!
本文致力於講述本領域中的一個新進展,推介一個剛剛發明的掃描團簇 (sweeping cluster) 算法。在此基礎上,我們展示如何運用這樣的算法,去解決量子二聚模型 (quantum dimer model, QDM)。如此成功案例,令人激動和歡愉。
2 解決QDM的掃描團簇算法
量子二聚模型 (QDM) 是從阻挫磁體和統計物理中產生的低能有效模型。這一模型,可以説是把 RVB 的圖像用一種簡化的方式寫在晶格上。QDM 要求每個格點上有且僅有一個最近程 (最近鄰) 的 dimer,其局域約束條件見圖 1 的正方晶格的 dimer 構型 (黑粗棒表示 dimer)。同樣,我們也可以定義三角、六角晶格等格子上的 dimer 構型。

相比於阻挫自旋等等更加複雜的問題,QDM 在系統的 Hilbert 空間上進行了截斷,去除高能子空間[1]。因此,QDM 是很多自旋模型和統計物理模型的低能有效描述。
這裏,我們通過其與阻挫 Ising 模型的映射[2]來給出説明。
圖2 左圖所示是一個三角晶格反鐵磁的 Ising 模型。這一模型高度阻挫,因為每個三角形的三個 Ising 自旋無法同時實現反鐵磁排列。在低能時,有所謂的三角形規則:每個三角形上必定有兩對反向的自旋和一對同向的自旋。現在,由三角形晶格出發構造其對偶的六角格子,如圖 2 左圖的黃色虛線構成的六邊形格子,每個格子中間有一個自旋。我們規定,同向自旋之間存在一個dimer (黃色棒槌);反向自旋之間則是普通的 link (黃色虛線段)。這個低能條件下的三角形規則,就與六角晶格每個格點有且僅有一個dimer 存在嚴格的映射關係。通過這個方式,我們可以把高能的自旋構型去掉。也就是説,dimer 模型的 Hilbert 空間是一個阻挫自旋模型的低能有效空間。
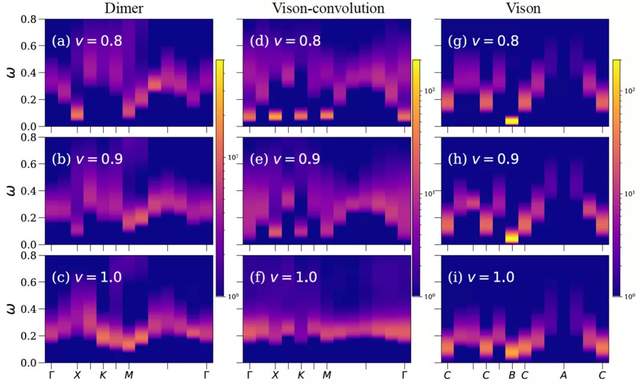
在阻挫量子 Ising 模型裏,自旋子 (spinon) 的激發表現為出現一個三自旋同向的三角形。這樣的激發違反了三角形規則,屬於系統的高能激發,很多時候可以不考慮。而dimer 模型抓住的是在spinon 激發能量之下的低能物理。比如,我們剛剛在《npj Quantum Materials》上發表的工作[3] (npj Quantum Materials 6, 39 (2021),https://www.nature.com/articles/s41535-021-00338-1),即是研究 vison (一種 Z2 拓撲序中的任意子) 的動力學性質。如果體系中存在 spinon 的激發,除了掩蓋 vison 激發信息之外,還使得 vison 本身的定義變得模糊。
同樣,對正方格子 Ising 模型,也可以定義類似的阻挫。以圖 2 右圖所示。自旋所在晶格上細的線段 (鍵) 定義為鐵磁,粗的線段 (鍵) 為反鐵磁。很顯然,這樣的規則難以得到全部滿足。晶格中一定存在一些違反這一規則的鍵,我們得到的只是一個低能的正方形規則:每個正方形上必定有一根線段上的自旋對,其能量不是最優的。這一線段處用一個 dimer 構型 (黃色的棒槌) 來表示,即有了約束條件。

經過如此這般考慮,正方晶格中的量子二聚模型 QDM 之哈密頓量一般寫為:


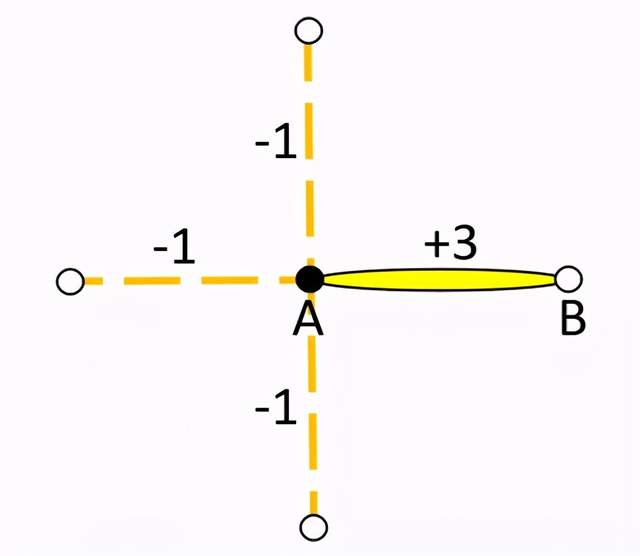
如圖 3 所示,在正方晶格上有黑色的 A 格點和白色的 B 格點兩套子格。在每個 link 上可以定義一個 flux:有 dimer (黃色棒槌) 的link 表示一個從 B 到 A 的 flux,數值為 3。沒有 dimer 的 link 表示一個從 B 到 A 的 flux,數值為 – 1。當把這樣的 flux 看成電場 E 時,可對 A 或者 B 點進行散度操作,即有 div E = 0。這是一個嚴格的格點高斯電磁場,也就是一個 U(1) 格點規範場。更有趣的是,當 t = V 時,即動能 t等於勢能 V時,此模型的基態是嚴格可解的,其基態波函數是一個標準的 RVB 態。這個嚴格可解的點稱之為 Rokhsar – Kivelson (RK) 點[5]。可見,QDM 模型正是一個可以找到自旋液體以及對應的拓撲序和任意子激發的好載體。
然而,QDM 有一個不同於其它如海森堡或者 XXZ 自旋模型的地方,就是它多了一個局域幾何限制條件 (local geometrical constraint):即每個格點上有且僅有一個最近程的 dimer 存在。對於這樣受限的 Hilbert 空間,雖然模型沒有符號問題,然而幾何限制條件讓其模擬求解變得十分繁瑣。之所以這樣説,是因為傳統的蒙特卡洛方法,不管是路徑積分的蠕蟲 (worm) 算法,還是 SSE 的圈 (loop) 更新方法,都不用考慮局域約束條件,算法只需要滿足模型的整體對稱性或者整體約束條件就行。比如,只要滿足總自旋守恆條件就行。換句話説,自旋的翻轉與否,和周邊的自旋構型無關。然而,QDM 被施加的局域幾何限制條件就不同了。如果把一個 link(鍵) 當作一個自旋,每個 link 也有兩個狀態:有 dimer 或沒有 dimer。如果此時只是翻轉單個 link 的狀態,即從佔據變成不佔據或者反之,則會破壞每個格點有且僅有一個 dimer 的約束條件。
那怎麼辦呢?為了滿足如此嚴格的約束條件,必須在每次蒙特卡洛更新的時候都要檢查是否違反了這一局域約束條件。這就是問題的難處,模擬時不光要在指數相空間中做高效更新,還得在每次更新時遵守局域約束條件,這就好比要帶着手銬和腳鐐跳舞:費時、費力、還難看!
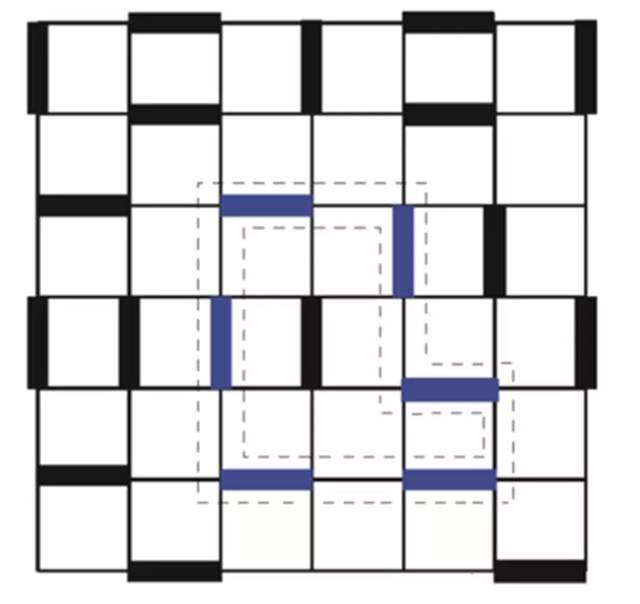
在經典的 dimer 模型 (即哈密頓量只有 V 項) 中,前人構造了首尾相接的 loop 算法[6],如圖 4 所示。很顯然,只要虛線包圍的路徑構成一個 loop,loop 內的 link 都翻轉,就依然可以滿足約束條件。但是,量子模型中還有一個t 項,系統在虛時方向需要用哈密頓量來演化,而不是隨機走一個圈而邊走邊翻轉 link 就行了。
這個哈密頓量演化條件讓問題變得極為複雜,應該怎麼設計量子dimer 模型之更新才能滿足這一約束條件呢?
這裏,該是我們的掃描團簇算法登場的時候了。眾所周知,一個 N 維量子模型,可以映射為一個 N + z 維的經典模型 (很多時候 z = 1)。量子蒙特卡洛的思路也正是如此,即通過虛時間軸 (imaginary time),將各個虛時間的經典構型連接在一起進行抽樣。因此,一個可行的解決方案應當如圖 5 所示:圖中每個虛時間對應一個經典構型層,層與層之間用量子演化算符聯繫起來,即基本的路徑積分思想。當我們對整個虛時間構型更新時,在每一層經典構型看來,都應該進行了 loop 更新以滿足約束條件,即如圖中藍線所示。同時,這些不同層的藍色 loop 之間還必然存在一些如紅線所示的更新線,來更新層間的量子演化算符,使得整個更新滿足路徑積分規則且遵從約束條件。
事實上,如此構想,很多前人都做過嘗試,但是沒有取得成功。問題的難處還是在於怎麼把局域的約束放進路徑積分的更新過程裏。

熟悉 SSE (隨機級數展開,stochastic series expansion) 的朋友都知道:虛時間內的算符和構型,可以用更新線來進行翻轉。同時,更新線其實也記錄了新的構型信息,可以被有效利用。這裏,我們正好可以利用更新線來記錄幾何限制,構造新的更新模式。在自旋模型的 SSE 算法中,更新線往往單獨行動,不受其它更新線的影響。而在約束條件下,如果讓所有更新線沿着虛時間方向一起更新,這樣就把約束條件記錄在更新線中、並同時帶到下一層。如果我們把虛時間想象成真的時間,那麼在每一個時刻只要我們做一些滿足約束條件的動作,下一個時刻,該構型勢必還是遵從約束條件的,然後再對它進行操作更新,如此繼續即可。這樣就可以在受限的 Hilbert 空間中實現滿足要求的更新。以前的量子蒙卡更新正是沒有在此處細心推敲,所以對約束只好束手無策。
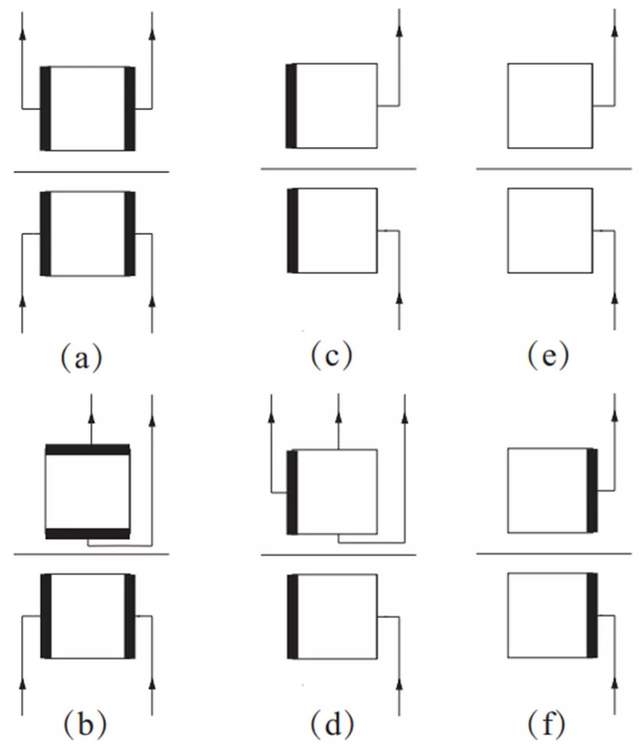
基於這樣的想法,可以把虛時間上哈密頓量算符對系統構型的更新操作用圖 6 這樣的圖表示出來。在圖 6 中,上 / 下方框表示算符作用後 / 前的 dimer 構型,中間的橫線是一個作用在該 plaquette 上的哈密頓量算符。舉個例子,比如 (a) 表示一個對角算符 (即哈密頓量中的 V項) 作用在一對平行 dimer 構型上後,其構型不變。類似的,(b) 表示一個非對角算符 (即哈密頓量中的 t 項) 作用在一對平行 dimer 構型上後,其構型改變。同時,為了遍歷性,量子蒙卡方法常常會在哈密頓量中添加常數項 (並不改變任何物理結果),如圖 6 (c)、(d)、(e)、(f) 就表示常數項作用在構型上,構型保持不變。另外,我們在圖中還會看到帶有箭頭的線,這些就是前文中提到的更新線。更新線所到之處,link 被翻轉,算符的種類隨之會發生改變。如圖 6 的例子,表現了當下方的更新線到達後,上方的更新線應該如何生長。比如 (a) 所示,下方的更新線到達之處,link 上的 dimer 被翻轉,即下方變成一個空的 plaquette。此時,只有常數項算符可以作用在這種構型上,所以中間橫線代表的算符必然是常數項,上面的構型也必然是一個空的 plaquette。所以,上面的兩個 dimer 需要被翻轉,即生長出兩條更新線。
值得注意的是,(c) 和 (d) 兩種情況下,下方的更新線到達後,都生成了一對平行的 dimer,而 t 項與 V 項都可以作用在一對平行 dimer 的構型上,從而可以有一個選擇自由度:即轉動這對 dimer (非對角算符) 還是不轉動 (對角算符),從中選擇 (c) 或者 (d) 繼續生長更新線。
有了這些設計之後,我們不妨看一個完整的團簇更新的例子。
以二維正方晶格 QDM 為例,將圖 5 的三維立體圖按照虛時間順序一層一層攤開,逐層解剖,以便仔細看看團簇更新是如何發生的。在圖 7 中,每一個小圖表示某一個特定虛時刻的構型,箭頭走向表示虛時間方向 ((a) 和 (b) 中各有 9 個構型)。“D” 和 “N” 表示作用在該方塊 (plaquette) 上的對角和非對角算符。再次特別提示,對角項並非單純的 V 項。為了更新的遍歷性,一般我們會在哈密頓量里加常數項,使得 plaq 中即使沒有平行 dimer 也有權重。非對角項即t 項。圖 7 (a) 和 (b) 表示團簇更新前和更新後的虛時 dimer 構型。更新後的圖中,紅色的 “D” 和 “N” 表示這裏要隨機選取兩種算符 (對角或者非對角) 中的一種,而我們隨機選取了紅色的這種。白色的小圓圈表示垂直紙面穿過該處的更新線,也就是説有圓圈的鍵 (link) 處需要翻轉。從每一層的虛時間切片看,的確是經典 dimer 型下的經典圈 (loop) 更新方法。從 (b) 中清晰可見,白色圓圈圍成的圈由小變大,再由大變小,最後生成一個三維的團簇並結束更新。

固然,到目前為止的描述仍然比較簡略。但是,通過這樣的基本規則和設計,可以成功實現一個約束體系的更新。這一實現過程,其實也完成了 QDM 對應的物理過程在 dimer 時空表象下的操作。再經過細緻平衡計算,可以給出具體的更新接收概率。此處不做進一步的展開,更多的細節參見文獻[7,8]。
因為更新是沿着虛時間方向展開,並且在更新過程中多線並行形成時空團簇,而團簇又在時空的掃描 (更新過程) 中不斷髮生變化。故而,我們將此方法命名為掃描團簇 (sweeping cluster) 算法[7, 8]。
3 應用於三角晶格QDM
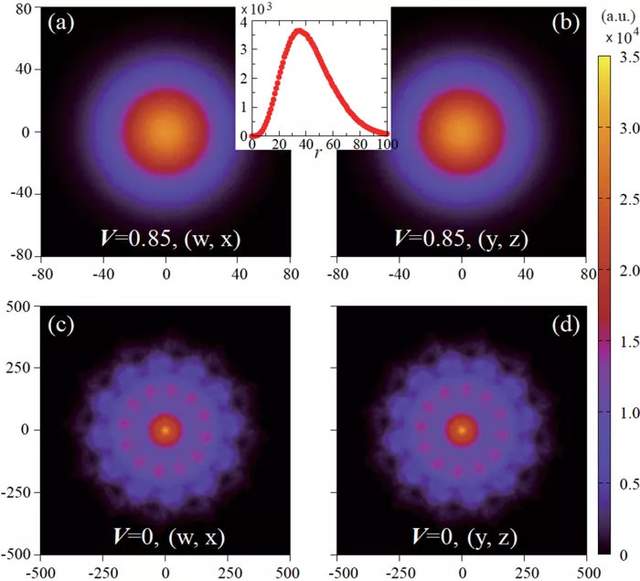
圖10. QSL – VBS 相變的序參量的統計分佈圖。因為此處的序參量生活在 4 維空間 (O(4) 對稱性),我們採用兩種方向的2維投影來表示。(a)、(b) 為相變點處的分佈圖 (V = 0.85),可以看到分佈接近正圓,説明序參量確實生活在 O(4) 球面上,具有湧現連續對稱性。(c)、(d) 為 VBS 序內部的分佈圖 (V = 0),可以看到由於對稱性發生破缺,此時序參量分佈在 O(4) 球面上的離散點處。
拼圖的最後一塊是 QSL – VBS 相變點的性質。前期的理論工作認為,由於 √12 × √12 的 VBS 複雜的對稱性破缺方式,這個相變點可能具有湧現 O(4) 對稱性。但是湧現連續對稱性這種事情還得靠重整化羣流動中的種種機緣巧合。這本身就是強關聯的問題,不是像平均場微擾論那樣心誠則靈的,需要數值計算來做無偏差檢驗。感興趣的讀者可以看看筆者舊文 [13],講的就是湧現連續對稱性在實際系統中不湧現的例子。

拉拉雜雜寫下這些,其實就是想把掃描團簇算法的發明及其在解決量子 dimer 模型中的應用過程推介給感興趣的讀者。正如本文引子中提到的,量子多體問題十分複雜,每一步算法的進步都推動着領域前進的紮實腳步。以代數量級的計算複雜度去征服指數量級的量子多體相空間,滲透着人們對於物理問題本身的深入理解。在算法設計中,也體現了緊密契合模型微觀物理過程的嘗試,以及對最新計算軟件硬件的熟練應用。當然,對量子多體問題的探索,最終還體現着人們對於問題本身深刻而豐富的物理內涵之深深眷戀和不懈求索。
無論如何,對於這些發明算法的人,也許他們在最終看破一切之後會遁入空門、逃進深山、避世嫉俗。但是,面對着 “以代數計算複雜度征服指數相空間”這樣庶幾的“人生有何意義”之終極問題,他們痛苦過、奮鬥過、成功過 (更多的時候是失敗過)。這樣結結實實、有血有肉的獨特體驗,是他們的光榮,更是他們的成績與自豪。
參考文獻
[1] Moessner, R., & Raman, K. S. (2011). Quantum dimer models. In Introduction to frustrated magnetism (pp. 437 - 479). Springer, Berlin, Heidelberg.
[2] Moessner, R., & Sondhi, S. L. (2001). Ising models of quantum frustration. Physical Review B 63, 224401.
[3] Yan, Z., Wang, Y. C., Ma, N., Qi, Y., & Meng, Z. Y. (2021). Topological phase transition and single / multi anyon dynamics of Z2 spin liquid, npj Quantum Materials 6, 39.
[4] Fradkin, E. (2013). Gauge theory, dimer models, and topological phases. In Field theoriesof condensed matter physics (pp. 286 - 342). Cambridge University Press.
[5] Rokhsar, D. S. and Kivelson, S. A. (1988). Superconductivity and the quantum hard-core dimer gas. Physical Review Letters 61, 2376.
[6] Alet, F., Jacobsen, J. L., Misguich, G., Pasquier,V., Mila, F., & Troyer, M. (2005). Interacting classical dimers on the square lattice. Physical Review Letters 94, 235702.
[7] Yan, Z., Wu, Y., Liu, C., Syljuåsen, O. F., Lou, J. & Chen, Y. (2019). Sweeping cluster algorithm for quantum spin systems with strong geometric restrictions. Physical Review B 99, 165135.
[8] Yan, Z. (2020). Improved sweeping cluster algorithm for quantum dimer model. arXiv preprint arXiv: 2011.08457.
[9] Misguich, G., & Mila, F. (2008). Quantum dimer model on the triangular lattice: Semiclassical and variational approaches to vison dispersion and condensation. Physical Review B 77, 134421.
[10] Ivanov, D. A. (2004). Vortex like elementary excitations in the Rokhsar - Kivelson dimer model on the triangular lattice. Physical Review B 70, 094430.
[11] Wang, Y. C., Cheng, M., Witczak - Krempa, W., & Meng, Z. Y. (2020). Fractionalized conductivity at topological phase transitions. arXiv preprint, arXiv: 2005.07337.
[12] Sun, G. Y., Wang, Y. C., Fang, C., Qi, Y., Cheng, M., & Meng, Z. Y. (2018). Dynamical signature of symmetry fractionalization in frustrated magnets. Physical Review Letters 121, 077201.
[13] 孟子楊,《學好蒙特卡洛,不會被忽悠》,https://mp.weixin.qq.com/s/1uqCWbKmIELOR8ehFvtSSw
備註
(1) 筆者嚴正、孟子楊,目前供職於香港大學。《瞧!這個人》是德國哲學家尼采的自傳,這裏借這個題目,取仰慕先賢“重估一切價值”的批判精神之意。
(2) 文首處的小詩為 Ising 所撰,表達對發展計算方法的物理人之敬意。
本文經授權轉載自微信公眾號“量子材料QuantumMaterials”。