還有人分不清咖啡杯和甜甜圈？數學家説，還真有_風聞

許多朋友聽説過關於“咖啡杯和甜甜圈是同一回事”的論述，也有許多朋友對於拓撲的最初印象也來自於此。但是拋開這個模糊的表述，我們有沒有辦法嚴格地去定義這一點呢？這就要用到我們今天的話題“同調論”的觀點了。

撰文 | Kelsey Houston-Edwards

翻譯 | xux

審校 | C&C

起初，拓撲學似乎是數學中一個異常不精確的分支。這是一門研究黏糊糊橡皮泥的學科，它的研究對象能夠無限地彎曲、拉伸和壓縮。但是也有一些限制：不能在形狀中創造或破壞洞。(一個古老的笑話：拓撲學家分不清咖啡杯和甜甜圈，因為它們都有一個洞。）雖然這似乎與代數的嚴謹相去甚遠，但一個叫做同調的強大想法幫助數學家連接了這兩個世界。

發明同調論起初是為了嚴格計算出“洞”的數量。同調論為數學思想提供了框架，讓我們能夠用一種新的方式來分析數據中的形狀。

“洞”這個詞在日常用語中有很多含義——泡泡、橡皮筋和碗的“洞”各不相同。數學家感興趣的是一種特殊類型的洞，這種洞可以被描述為一個封閉且中空的空間。一維的孔看起來像橡皮筋。橡皮筋的曲線是封閉的（不像一根鬆散的繩子）和中空的（不像一元硬幣的周界）。

洞、非封閉、非中空

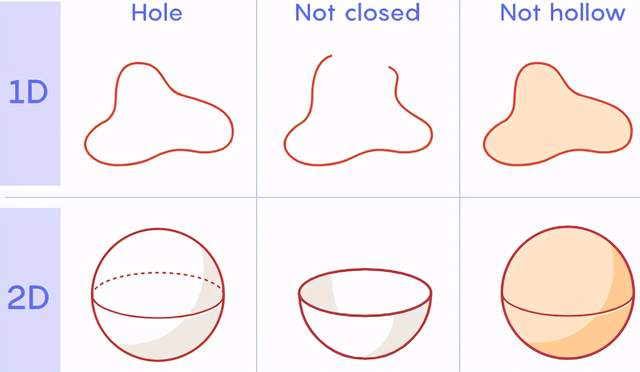
將這個邏輯擴展下去，那麼二維洞便是一個空心球。數學家們正在尋找的這種洞，是像籃球那樣封閉且中空的，而不是像碗或保齡球上的洞。

但是數學是嚴謹的，雖然用這種方式思考，能夠讓我們直觀地想到橡皮筋和籃球，但它還不夠精確，不足以作為一個數學定義。例如，它不能清楚地描述更高維度的洞，你也不能編程讓計算機區分封閉空間和中空空間。

密歇根州立大學的何塞·佩雷亞説：“對於洞，沒有一個好的定義。

相反，同調從物體的邊界推斷出物體的洞，這是一個更為精確的數學概念。想要研究物體上的洞，數學家只需要知道物體邊界的信息。

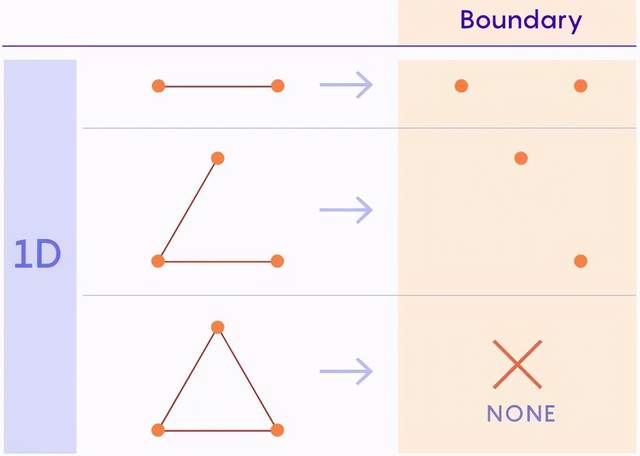
形狀的邊界是其外週上點的集合，邊界總是比形狀本身低一個維度。例如，一維線段的邊界由兩端的兩點組成。（點是零維的。）實心三角形的邊界是由一維邊線組成的空心三角形。同樣，實心稜錐的外邊界是空心稜錐。

不同維度的形狀的邊界（boundary）

如果將兩條線段粘在一起，它們相交的邊界點將消失。邊界點就像懸崖的邊緣——它們幾乎要從直線上掉下來。但是當你將這些線連在一起時，邊界上的點就會安全地呆在中心。另外，這兩條線總共有四個邊界點，但當它們粘在一起時，生成的形狀只有兩個邊界點。

如果再加一條邊，讓結構封閉起來，形成一個空心三角形，那麼邊界點就消失了。組成三角形的三條邊的每個邊界點與另一個邊界點兩兩相消，空心三角形沒有邊界。因此，每當一組線形成一個圈時，邊界就不復存在。

一個環（loop）繞回到它的起點會圈起來一片區域。但只有當環包圍區域是空的時，才能稱之為一個洞（hole），就像橡皮筋一樣。畫在紙上的圓形成一個環，但它不是一個洞，因為中心被填滿了，這個圈是二維區域的邊界。

因此，洞具有兩個重要且嚴格的特徵。首先，洞沒有邊界，因為它是封閉的。第二，洞不是其他東西的邊界，因為洞本身必須是中空的。

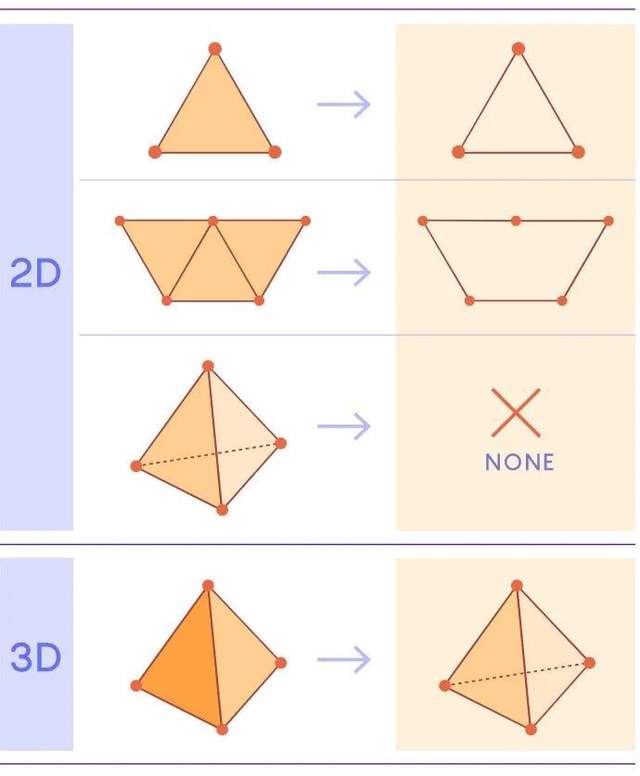
這個定義可以擴展到更高的維度。二維實心三角形有三條邊。如果將幾個三角形連接在一起，一些邊界邊就會消失。當四個三角形排列成一個稜錐時，每一條邊與另一條邊相消。所以稜錐的面沒有邊界。如果稜錐是空心的，那麼，它就不是一個三維實體塊的邊界，這時它就形成了一個二維洞。

為了在一個特定的拓撲圖形中找到所有類型的洞，數學家們建立了一個叫做鏈復形的東西，它為同調論搭起了框架。

鏈復形

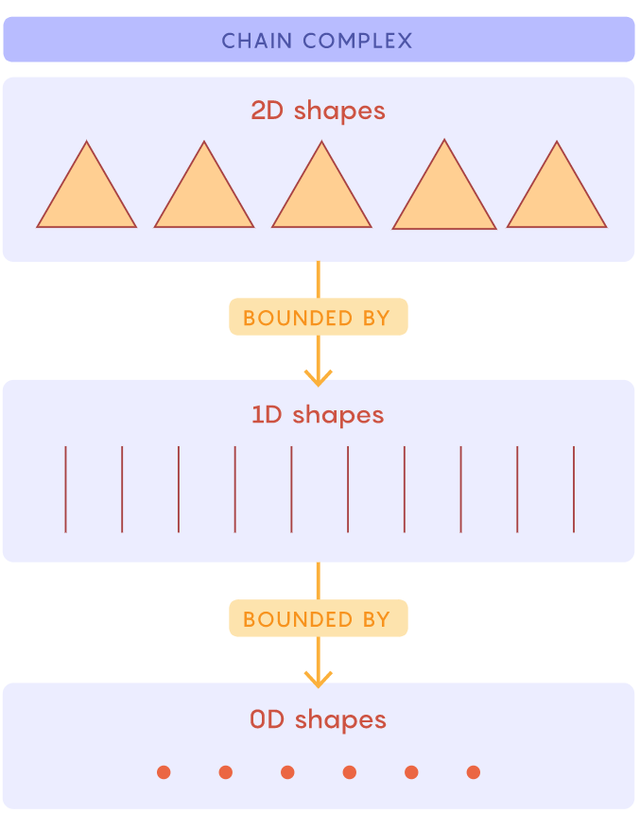
許多拓撲形狀可以通過把不同尺寸的部分粘在一起形成。鏈復形是一個圖表，它給出了一個幾何圖形的裝配説明。圖形的各個部分按維度分組，然後按層級排列：第一層包含所有點，下一層包含所有線，依此類推。(還有一個空的第零級，它只是作為基礎。）每一層都通過箭頭連接到下面的一層，這表明它們是如何粘合在一起的。例如，實心三角形連接到構成其邊界的三條邊。

數學家從鏈復形中提取圖形的同調，鏈復形提供了有關形狀組成部分及其邊界的結構化數據，這正是描述每個維度上的洞所需要的。使用鏈復形時，查找10維洞和一維洞的過程幾乎相同（只是其中一個比另一個更難可視化）。

同調的定義足夠嚴格，計算機可以用它來尋找和計算洞的數量，這有助於建立數學中通常需要的嚴格性。它還允許研究人員將同調用於越來越流行的用途：分析數據。

這是因為數據能夠可視化為浮在空間中的點。這些數據點可以表示物理對象（如傳感器）的位置，也可以表示抽象空間中的位置（如食物偏好的描述），附近的點表示具有相似味覺的人。

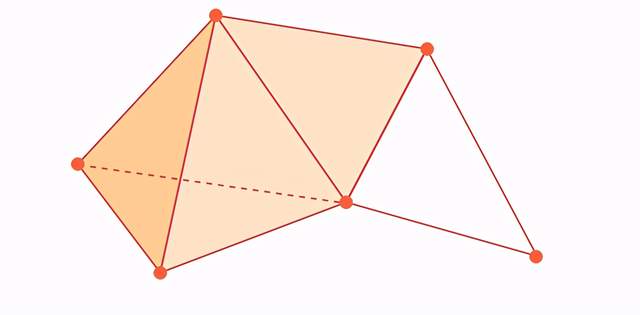
為了從數據中產生圖形，數學家在相鄰的點之間畫線。當三個點靠得很近時，它們被填充成一個實心三角形。當大量的點聚集在一起時，它們會形成更復雜、更高維的形狀。填充數據點會給它們帶來紋理和體積——從這些點創造出一個圖像。

同調將這個模糊形狀的世界轉化為嚴格的代數世界，代數是研究特殊數值結構和對稱性的數學分支。數學家在同調代數領域研究這些代數結構的性質。從代數中，他們間接地瞭解到有關數據的原始拓撲形狀的信息。同調有很多種，它們都與代數有關。

“同調是一種常見的結構。麻省理工學院的瑪吉·米勒説：“關於它，我們知道很多代數知識。”

同調提供的信息甚至可以解釋數據的不精確性：如果數據只是稍微移動，洞的數量應該保持不變。當處理大量的數據時，這些洞可以顯示出重要的特徵。例如，時變數據中的循環可以表示週期性。其他維度中的洞可以顯示數據中的簇（cluster）和空缺（void）。

賓夕法尼亞大學的羅伯特·格里斯特説：“真正的推動力是要有一種魯棒性的方法，能夠從數據中提取出定性特徵。這就是同調帶給我們的。”

本文經授權轉載自微信公眾號“中科院物理所”，原題目為《孩子分不清咖啡杯和甜甜圈，竟是因為……》。

原文鏈接：https://www.quantamagazine.org/how-mathematicians-use-homology-to-make-sense-of-topology-20210511/