哈爾莫斯,我的懷念_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2021-05-22 08:21
我以能成為教師而驕傲,教書是一個如蜉蝣般朝生暮死的事業,就像拉小提琴,樂曲結束就完了,教師給學生上課也是一樣,而寫作是一個永久的事業,雖然辛苦,可是我歡喜。
——哈爾莫斯
撰文 | 林開亮
引言
我之所以成長為一名數學工作者,並熱衷於幾何觀點下的線性代數,與一個人有很大的關係,這個人就是美國數學家哈爾莫斯(Paul Richard Halmos,1916–2006)。我第一次接觸到哈爾莫斯,是通過他的數學自傳《我要作數學家》[1]。不記得是大一還是大二,當時我在南開大學數學院的圖書資料室閒逛,偶然看到這本書。翻開前幾頁,我立刻就迷上了它。哈爾莫斯寫道(文獻[1],p. 4):
我主張講解問題要多用文字少用數字,特別是講解數學時要這樣做。在數學中,創造精妙的符號體系(以表示乘積、方冪、級數、積分等一切計算概念),常常是一大進步,然而,使用符號雖然能簡化計算,同樣也會導致概念變得晦澀難懂。
接下來哈爾莫斯舉了一個例子來説明文字的優越性,他只用一句話就點透了內積空間中著名的貝塞爾(F. Bessel)不等式的證明,令我大開眼界,並永誌不忘。我覺得自己學到了妙招,在此之前我從未聽到有老師這樣講數學。
再往下翻下去,我讀到了更多有趣的東西,也得到了更多的實惠,比如知道了《美國數學月刊》、哈代(G. H. Hardy)的名著《純數學教程》、加德納(M. Gardner)的數學小品、卡普蘭斯基(I. Kaplansky)、麥基(G. Mackey) 等數學名家編寫的優秀數學教材——以至於從此以後,我都對哈爾莫斯深懷感激之情;在他誕辰100週年之際,我決定給大家講一講我眼中的哈爾莫斯。完整描述哈爾莫斯非筆者能力所及,這裏只給出一個概貌。有興趣進一步瞭解的朋友可以去翻閲[1]以及他那本著名的《我有一本相冊回憶錄》 。

哈爾莫斯於1916年3月3日出生於匈牙利布達佩斯,是猶太人。父親是醫生。母親去世後,父親移民到美國另立家室。哈爾莫斯13歲被父親接到芝加哥,從此成了美國人。據哈爾莫斯説,他的繼母“像解極值問題一樣對待生活中的每件事情”。為了節省學費,繼母找人幫忙,讓哈爾莫斯直接插班高二。當然之所以能夠順利跳級,主要還是因為哈爾莫斯聰明。
哈爾莫斯很快就掌握了英語。高中畢業後,為了追求自由,哈爾莫斯選擇了離家更遠的伊利諾伊大學,而不是數學實力更雄厚、陣容更強大的且位於近水樓台的芝加哥大學。1931年9月,15歲的哈爾莫斯在伊利諾伊大學註冊,專業是化學工程。哈爾莫斯很快發現,自己對化學實驗不感興趣——用他本人的話説,“完成實驗報告就像在作假帳”。於是他轉到數學系。
大一時他修了三門數學課:代數、三角、解析幾何。只有解析幾何是新東西,可惜當時並沒有學習線性代數(矩陣和向量),他對所謂的“化簡”和“旋轉”不得要領。大二時他修了空間解析幾何與微積分(當時認為微積分對大一學生來説還太難了),用的教材是Granville–Smith–Longley的《微積分》。哈爾莫斯很憎惡這本書,不懂作者到底在説些什麼。直到大二快結束時,哈爾莫斯才“越來越確信,主修數學算是找對了方向。”大三時哈爾莫斯修了三門數學課:高等代數、高等微積分、射影幾何。教射影幾何的萊維(H. Levy)很喜歡哈爾莫斯,曾帶他到數學圖書館,教他使用數學文獻。後來萊維指導了哈爾莫斯的本科學位論文。大四時,哈爾莫斯又修了三門數學課:高等歐幾里得幾何、數學的基本概念、概率論。這些課程留給他的感覺,更多是神秘而非美妙。
總的來説,由於當時伊利諾伊大學的絕大部分數學教師都不搞數學研究(甚至連教學都成問題),哈爾莫斯本科階段沒有打好數學基礎,他是這樣回顧其本科生涯的(文獻[1],p.45):
我的以數學為主修科的本科教育,就這樣匆匆而過。在數學方面,我不僅缺乏啓迪,而且無知得驚人。Weierstrass,Hausdorff,Poincaré,Galois和Cayley,對我而言,純粹是傳聞;我對正經的分析、點集拓撲、代數拓撲、抽象代數、甚至是4階方陣乘法之外的線性代數,一無所知。
1934年,哈爾莫斯本科畢業。之後繼續在伊利諾伊研究生院深造。他起初選的是哲學專業(早在大二時,他就通過邏輯課對哲學發生了興趣),同時也修統計課,以保持對數學的興趣。大概是他在哲學方面沒什麼天分,在1935年的哲學碩士學位的綜合口試中掛了,這斷了他的哲學路。不過好在他還有數學這條後路,哈爾莫斯因此正式轉為數學研究生。
哈爾莫斯修的頭三門研究生數學課是代數、分析和數論。代數用的是博謝(M. Bôcher)的教材,哈爾莫斯發現很難,他後來這樣評價這本書(文獻[1], p.51):
我做學生的時候,我們用的矩陣論的教材是博謝的老得掉牙的書(我認為寫得一團糟),我在這個科目上花的大量時間當中,我的主要情緒是惱火,有時甚至達到憤怒。……直到四五年以後,在我已經取得博士學位、聽馮·諾依曼(J. von Neumann)講算子理論以後,我才真正開始懂得這個科目是講什麼的。

做這個題目——我第一次發表的研究成果——不需要任何靈感,只需要耐心和勤奮,多應用卡邁克爾教給我的那些技術。但這項工作給了我一種成就感和我可以做研究的信心(這是極其需要的)。我非常得意,買了200份抽印本。結果,等到好多年後,我才全部送完。
不過哈爾莫斯覺得自己突然躍遷為真正數學家的那一刻,是在1936年4月的某一天,他突然對分析有了頓悟,對此他記憶猶新(文獻[1],p.61):
天色破曉時——我記得彼時的情景——安布羅斯(W. Ambrose)和我在教學樓二層的一間討論室裏談話,他的一些話可謂是讓我撥雲見日所需的最後一抹陽光。突
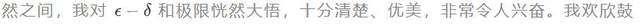
儘管哈爾莫斯在那一刻對分析有感覺了,但他並沒有立即喜歡上分析。他最終熱愛上分析,要歸因於年輕教員杜布(J. L. Doob)的影響。杜布1935年來到伊利諾伊,這對哈爾莫斯來説意義非凡。事實上,杜布後來成了哈爾莫斯的博士學位論文指導老師。1938年,哈爾莫斯以學位論文《隨機變換的不變量:賭博系統的一般理論》獲得博士學位。哈爾莫斯是杜布門下的第一個博士,而他的死黨安布羅斯則於次年成為杜布的第二個博士。(杜布一共培養了16名博士,除了哈爾莫斯和安布羅斯,還有David H. Blackwell和周元燊(1924–)。)

哈爾莫斯在母校的教學和研究並不順利,一年後安布羅斯被普林斯頓高等研究院接收為博士後研究員。哈爾莫斯認為這是個好機會,於是請求母校放行,允許他同去高等研究院遊學訪問。
普林斯頓遇貴人
高等研究院坐落在普林斯頓,離普林斯頓大學不遠,當時已成為數學世界的中心,哈爾莫斯在這裏結識了許多後來成名的大數學家,從他們那裏學到了許多東西。幸虧他的匈牙利同胞馮·諾依曼慧眼識珠,哈爾莫斯在第二個學期就被高等研究院接收為正式研究員。哈爾莫斯之所以被馮·諾依曼相中,是因為馮·諾依曼看了哈爾莫斯所記的線性代數筆記,非常滿意。哈爾莫斯覺得馮·諾依曼的講課優美而富有啓發性,後來自發為普林斯頓大學的研究生講授馮·諾依曼觀點下的線性代數,取得了空前的成功。他又根據學生記下的筆記,寫成了他的第一本數學著作《有限維向量空間》[2]。在馮·諾依曼的幫助下,該書於1942年作為普林斯頓數學研究叢書第7號出版。

我讀龐特里亞金的《拓撲羣》,雷默(E. Lehmer)夫人的英譯本剛出版,這是一本讓人開眼界的書,給人啓發、令人激動的書。真的,像讀偵探小説,要找到案件的主謀。哈爾莫斯在普林斯頓高等研究院一共待了三年(1939–1942),其間產生了兩項合作研究,一項是與馮·諾依曼關於遍歷理論的合作,一項是與薩默爾森(H. Samelson)關於拓撲羣的合作。跟他的《有限維向量空間》一樣,這兩個工作都發表於1942年。
芝加哥黃金時代
普林斯頓時代結束後,哈爾莫斯重新回到伊利諾伊,不過一年後他轉到錫拉丘茲,直到1946年9月,他換到了更好的大學——芝加哥大學,由此而開啓了他生命中最令人振奮和富有成果的階段。
當時斯通被芝加哥大學任命為新的數學系主任,數學系也因此而迎來了輝煌的斯通時代。哈爾莫斯之所以能收到芝加哥大學的聘書,與斯通的提名密切相關。在上世紀50年代,芝加哥大學數學系有四位名滿天下的數學家坐鎮,他們分別是:韋伊(A. Weil)、陳省身、麥克萊恩(S. MacLane)和齊格蒙德(A. Zygmund)。這幫助芝加哥大學吸引來不少傑出的學生,比如日後成為享譽世界的數學人物的湯普森(J. G. Thompson)、柯恩(P. J. Cohen)、斯坦(E. M. Stein)、辛格(I. M. Singer)、卡爾德倫 (A. P. Calderón) 等。儘管哈爾莫斯無法跟陳省身、韋伊等大牛比肩,但他仍吸引了九名優秀的學生作為博士研究生,其中他最引以為豪是畢曉普(E. Bishop),構造性分析的創始人。
在教學方面,哈爾莫斯雖然自認為是一個很優秀的教師,但芝加哥大學的學生很有才華而且非常用功,於是教學也是一大挑戰,哈爾莫斯非常努力地讓自己成為一名更優秀的教師。例如,他在每一個班幹得的第一件事情就是儘快瞭解他的學生。為此,他要求學生坐在自己想做的位置,但要求固定座位,以便他記住每一個人。他甚至還通過漫畫來記住學生的特徵:長頭髮、圓臉、牛角鏡框等。如果班上學生不多,他會要求每位學生在開學一兩週內去辦公室跟他閒聊,瞭解他們的大致情況(來自哪裏,高中是否學過微積分,想學什麼,哪門課程有困難……),讓學生真真切切感受到,一位近在咫尺的教授正實實在在地關心着他們的成長。
在研究方面,哈爾莫斯開始實踐他的一個信念:為保持活力,必須每五年更換一個領域。因此,他先後研究了許多領域:希爾伯特空間、測度論、遍歷理論、邏輯學。前三個領域是受杜布和馮·諾依曼的影響,對邏輯學的興趣則源於羅素(B. Russell)的通俗著作和羅素與懷特海(A. N. Whitehead)的經典著作《數學原理》。
作家哈爾莫斯
我以能成為教師而驕傲,教書是一個如蜉蝣般朝生暮死的事業,就像拉小提琴,樂曲結束就完了,教師給學生上課也是一樣,一門課程上完就結束了,而寫作是一個永久的事業,雖然辛苦,可是我歡喜。
哈爾莫斯
哈爾莫斯非常擅長寫書,他在許多領域都有專著,其中《測度論》[3]和《希爾伯特空間問題集》[4]列入他所主編的研究生數學叢書 (Graduate Texts in Mathematics,常縮寫為GTM)第18號和第19號,並且都有中譯本 ;而《布爾代數講義》和《樸素集合論》則與新版本的《有限維向量空間》一起列入他所主編的本科生數學叢書(Undergraduate Texts in Mathematics,常縮寫為UTM)的前三本,其中《布爾代數講義》的新版本《布爾代數引論》作為UTM第128號於2009年出版,這是由哈爾莫斯與葛範德(Steven Givant)合作完成的。特別要提到《希爾伯特空間問題集》一書,據哈爾莫斯講,第一版全書共有199個問題,他逼迫自己每天必須寫一個問題,但是事實上,完成此書花了他三倍的時間。哈爾莫斯認為,他寫的書中,最好的也許就是《希爾伯特空間問題集》和《有限維向量空間》。對於大一大二的本科生,我們還特別推薦一下他的《線性代數問題集》[5]。另外,哈爾莫斯還編了一本《寫給數學愛好者的新老問題》[6]。
哈爾莫斯的三本數學問題集,正是體現了他的一項特殊才能:善於提出問題。哈爾莫斯注意到習題的價值,可能受到他的同胞、匈牙利數學家波利亞(G. Pólya)與舍貴(G. Szegö)的兩卷本經典《分析中的問題和定理》 的影響。波利亞–舍貴的書培育了好幾代數學家,從我國的老前輩徐利治(1920–2019),到加州大學的年輕俄國女數學家霍爾茨(O. Holtz ,1973–),都曾從中受益(見Olga Holtz,My Random Walks with Pólya and Szegö. 對於徐利治的情況,可見徐利治、袁向東、郭金海《徐利治訪談錄》(湖南教育出版社,2009年)第七章)。該書收入的不少問題直接取自數學論文,因此難度較大,不少成名數學家在學生時代甚至患有所謂“波利亞–舍貴恐懼症”。哈爾莫斯的習題集似乎鋪墊得更舒服些,因為他處理的主題比較集中,他好像也更擅長組織和整理。

教師哈爾莫斯


數學家哈爾莫斯
作為研究型數學家,哈爾莫斯固然小有成就 ,但並不耀眼,特別是在他所處的芝加哥數學系的輝煌背景反襯下。當麥克萊恩接替斯通成為系主任以後,想要以一流數學家取代二流數學家,以造就“全球當之無愧的最好的數學系”。哈爾莫斯的研究沒有得到他的認可,遭到排擠。1960年底,哈爾莫斯接受密歇根大學的邀請,離開了芝加哥。(根據麥克萊恩寫的關於芝加哥大學數學系的歷史文章https://celebratio.org/MacLane_S/article/459/,芝加哥大學的“斯通時代”在1960年左右結束。Weil於1958年去了普林斯頓高等研究院,陳省身和Spanier 於1959年去了伯克利, Segal於1960年去了MIT。)他在密歇根帶了6名博士研究生,其中最突出的是薩拉森(D. Sarason)。他後來説,他無法判斷薩拉森和畢曉普究竟哪一個更優秀。此後,哈爾莫斯曾先後任教於加州大學聖塔芭芭拉分校、夏威夷大學和印第安納大學,1985年從印第安納大學退休。他的《我要作數學家》也正是在那一年出版。
哈爾莫斯在自傳中用第十二章的全部篇幅講“怎樣教書”,而在第十四章只有一小節講“怎樣做研究” 。他認為這個主題是很難講的,因為“如何做研究這個過程主要部分是心理上的,是難以描述的。”儘管如此,他還是儘可能地分享了他本人的研究心得——從特殊情形和具體例子出發:“所有偉大數學的源泉,都是特殊情形,都是具體例子。”這也是他寫文章、作報告的一貫宗旨。特別的,想要對此獲得切身感受的讀者可以參考他在台灣中央研究院數學所做的報告記錄[8]。哈爾莫斯本人對這個報告很滿意(文獻[1],p.436):
我很幸運:結果有一個很小的具體特例,其中涵蓋了所需理解的一切概念、所需克服的一切困難。於是我的報告着重於這個特殊情形。我感到很自豪:我覺得我成功地講述了一個漂亮的問題及其滿意的解答,而不必陷於無關的分析技巧的泥沼之中。

迪厄多內禮貌且友好,但事後明顯表現出不屑一顧的態度;我記不清他的原話了,但大意是,他祝賀我的滑稽表演,整個報告留給他的印象似乎是“趣味數學”。這在他的詞彙中是個譏諷的字眼;他認為我的報告趣味有餘,但是十分做作,流於膚淺。然而我認為(並一直認為),報告可遠遠超出這種水平。我倆評價的不同源於我們觀點上的差別。我想,對於迪厄多內來説,重要的是那個強大的一般性定理,從這一定理你很容易推出所有你需要的特例來;而對我來説,最偉大的前進步驟是,很能説明問題的中心例子,從這一例子中我們很容易搞清楚該例子周圍的所有具有普遍性的東西。
也許我們從迪厄多內這一方面可以側面理解,為何麥克萊恩不大認可哈爾莫斯的數學成就了。迪厄多內是著名的布爾巴基(N. Bourbaki)學派的代言人與筆桿子,他們提倡的是一般化、公理化;麥克萊恩曾與布爾巴基的成員艾倫伯格(S. Eilenberg)開創抽象的範疇論,他跟迪厄多內更容易產生共鳴。大致説來,數學家分兩類,一類是提問解題者,一類是理論創建者。哈爾莫斯屬於前者,布爾巴基成員和麥克萊恩屬於後者。正如哈爾莫斯自己所言,作為數學家,他最大的強項在於,在某些情況下,能看出兩個東西“相同”。雖然他對自己的數學成就總的評價並不高,不過他仍然因為曾經發現了一些美妙的東西而感到欣慰。他自認為,他最接近永垂不朽的數學貢獻是

除了教學和研究,哈爾莫斯還積極參與了許多服務,比如當編輯。作為編輯,哈爾莫斯除了與人合作主編UTM和GTM教學叢書以外,還主編過研究成果叢書、數學中的問題集(Problem Books in Mathematics)叢書,蓋伊(R. K. Guy)的《數論中未解決的問題》(有中譯本)以及《伯克利數學問題集》就屬於後者。哈爾莫斯還曾在1982–1986年間擔任著名的普及性數學期刊《美國數學月刊》(American Mathematical Monthly,以下簡稱《月刊》)的主編。
《月刊》是世界上發行量最大的數學期刊,而且(據哈爾莫斯推測)可能是讀者最多的數學期刊。事實上,如果哈爾莫斯知道,中科院數學所與中央研究院數學所各自主編的普及刊物《數學譯林》與《數學傳播》有很大一部分文章就譯自《月刊》的話,他就不會那麼保守了。
除了闡述性文章,哈爾莫斯還擅長寫書評。他曾負責編輯《美國數學會通報》(Bulletin of AMS)的書評專欄,而他在50年代曾寫過14篇書評(例如評過波利亞的《數學與猜想》)。1988年,美國數學會成立一百週年,哈爾莫斯寫過一篇精彩的書評《友誼地久天長的數學書》 。(Halmos, Some books of auld lang syne. A Century of Mathematics in America, Part I, pp. 131–174, Hist. Math. 1, Amer. Math. Soc., Providence, RI, 1988.)
哈爾莫斯在任期間,為這份刊物的傾注了許多心血。美國數學協會曾專門設立一個針對《月刊》中優秀綜述文章的獎項,名叫福特獎,2012年更名為哈爾莫斯–福特獎(Paul R. Halmos – Lester R. Ford Awards) ,以表示對兩位主編福特(Lester R. Ford,1942–1946年間任主編)和哈爾莫斯 工作的高度認可。Halmos本人就兩度獲得佛特獎(1971年https://www.maa.org/programs/maa-awards/writing-awards/finite-dimensional-hilbert-spaces, 1977年https://www.maa.org/programs/maa-awards/writing-awards/american-mathematics-from-1940-to-the-day-before-yesterday)。2016年,陸志勤與其合作者羅利特(Julie Rowlett)以其文章《對稱的聲音》 (Zhiqin Lu and Julie Rowlett, The Sound of Symmetry,The American Mathematical Monthly, vol. 122, no. 9, November 2015.)而榮獲這一獎項。
“他那個時代最優秀的數學闡述作者”
早在1944年,28歲的哈爾莫斯就寫出了人生中第一篇綜述文章《概率之基礎》(Halmos, The Foundations of Probability, The American Mathematical Monthly, Vol. 51, (1944), pp. 493-510.),並於兩年後獲得了美國數學協會頒發的查文尼特寫作獎(Chauvenet Prize)。正是這篇文章開啓了哈爾莫斯的綜述文章寫作的生涯,他的代表性綜述文章(http://www-groups.dcs.st-and.ac.uk/history/Extras/Halmos_popular_papers.html 有部分文章的介紹)彙集在其論文選第二卷《綜述寫作》,其中有許多名篇都已經譯成中文,如《1940年以來的美國數學》[7]、《數學的心臟》[8]、《解題的教學》 [9]、《如何寫數學》 [10]、《如何講數學》[11] 等。(我們正在籌劃編輯一本Halmos文集。)
如前所述,哈爾莫斯既是數學家、也是教師、編輯和作者,而他自認為他作為作者的成就最高。對此, MIT的數學家Gian-Carlo Rota曾在《我要作數學家》的書評(G-C Rota, Review: I Want to Be a Mathematician: An Automathography, by Paul R Halmos, Amer. Math. Monthly 94 (7) (1987), 700-702.)中特別寫道:“Halmos現在被認為是他那個時代最優秀的數學闡述作者。”
除了查文尼特獎,哈爾莫斯還獲得了美國數學協會1983年度波利亞寫作獎(George Pólya Award)。哈爾莫斯由於其闡述性文章方面的傑出貢獻而榮獲了美國數學會(AMS)1983年頒發的斯蒂爾數學著述獎(Leroy P. Steele Prize for Mathematical Exposition) ,其頒獎詞如下:
斯蒂爾數學著述獎授予保羅·哈爾莫斯,以表彰他寫出了許多處理有限維向量空間、測度論、遍歷論和希爾伯特空間的研究生數學教材。這些書中有許多是相關課題中用英文的首次系統闡述。這些著作的巧妙風格和內容對北美的數學教學產生了廣泛的影響。他關於如何寫作、如何談論和如何發表數學的文章,曾幫助所有的數學家更有效地交流思想和成果。
對此,哈爾莫斯做了精彩的答謝(此處中譯文改自胥鳴偉老師的譯稿《Halmos:他的原話》,作者J. Ewing,見《數學譯林》2009年第2期,148-160頁。):
不久前我偶然發現一篇標題為 “對兩個以上爭議進行表決的方法”的文章.你可知道,或者你能猜到,它的作者是誰嗎?那麼對於一篇標題為“論緊羣的自同構”又如何呢?誰寫的?第一個問題的答案是道奇森(C. L. Dodgson),更廣為人知的名字是劉易斯·卡羅爾 (Lewis Carroll),而第二個問題的答案則是保羅·哈爾莫斯。劉易斯·卡羅爾和我的共同點是,我們都被稱做為數學家,都努力做研究工作,並且我們都非常認真地努力擴大數學真理的所知範圍。為了謀生,劉易斯·卡羅爾當了教師,而僅僅是為了好玩,也因為他愛好講故事,所以他寫了《阿麗絲漫遊奇境記》(Alice’s Adventures in Wondeland) 。為了謀生,我當了近50 年的教師,而只是為了好玩,也因為喜歡,我愛好組織文字和闡明問題,所以我寫了《有限維向量空間》。那麼結果如何呢?我估計讀過 “對兩個以上爭議進行表決的方法”或者“論緊羣的自同構”的人屈指可數,然而劉易斯·卡羅爾卻因愛麗絲的故事而流芳百世,我也榮獲了關於闡述性數學著作的斯蒂爾獎。我不知道尊敬的道奇森先生對於名聲是怎樣想的,而我本人,則一直受到清教徒般的道德標準的教育:如果某件事好玩,那麼做這件事就不應該計較認可與回報。因此結果是,在我確實感到驕傲和快樂的同時,也不禁感到有點憂慮和懊悔。
我喜歡學習,探究,進行理解,而後則是解釋,但是接下來的把我所知道的傳遞給別人總非易事;它可能是極其艱難的。要解釋某件事,你必須不僅要加進一些東西還要有所保留;你必須知道什麼時候講出全部真實的東西,什麼時候跳過正確的思想而説些無傷大雅的閒言碎語。寫闡述性文章的困難不在於文章的風格、語句的斟酌,而是結構、文章的組織。誠然,語句是重要的,但是素材的安排,指出它的各部分間的相互關聯,以及與數學其它部分的關聯,並恰當地強調指出哪些是容易的,而哪些應該加以小心地處理,這些才是重要得多的……
作為回報、更是對優秀的作者的鼓勵,哈爾莫斯和他夫人弗吉尼亞·哈爾莫斯(Virginia Halmos)(他們1945年結婚,沒有子女。)向美國數學協會慷慨捐助,在2005年設立了歐拉圖書獎(Euler Book Prize),以表彰那些改觀了公眾對數學觀點的通俗書籍作者。之所以命名為歐拉獎,是因為擬定首屆頒獎在歐拉誕辰300週年的2007年。最近國內引進翻譯的好幾本數學科普書,就榮列歐拉圖書獎榜單:《素數之戀》、《普林斯頓數學指南》、《x的奇幻之旅》、《改變世界的17個方程式》、《魔鬼數學:大數據時代,數學思維的力量》、《魔法數學:大魔術的數學靈魂》、《愛與數學》、《算法霸權》。
在2005年,杜布去世後的第二年,哈爾莫斯夫婦捐助美國數學會設立了杜布獎(Joseph L. Doob Prize),每三年頒發一次,授予影響深遠的研究類書籍的作者。從2005起開始授獎,目前已頒獎四次,2005年和2014年的獲獎者分別是瑟斯頓(W. P. Thurston)和維拉尼(C. Villani)。
小結

哈爾莫斯從小就愛文字勝過數字。常言道“三歲看老”,他成功地發揮了自己的文字天才,成為了一位舉足輕重的數學著作家和數學編輯。哈爾莫斯清晰精煉的數學著作,讓許許多多的年輕人受益。例如,普林斯頓大學的數學教授馬瑟(J. N. Mather),在高中時代曾自學過不少數學書籍,但他真正讀懂的只有一本,就是哈爾莫斯的《有限維向量空間》。
哈爾莫斯及其合作者主編的UTM、GTM叢書已經排列在千千萬萬個圖書館的數學書架,惠及了世界各地一代又一代的數學新人。特別是在中國,世界圖書出版公司引進了影印版,為數學系的師生提供了便利。GTM叢書在國內被作為研究生教材普遍採用,我們期待UTM叢書也將得到本科師生的青睞,特別地,筆者這裏向所有數學本科生強烈推薦UTM第1號:《有限維向量空間》。它會讓你大開眼界,發現簡練的文字與優美的數學,讓你感受到從幾何的觀點來理解線性代數的激動與喜悦!
十多年前,我通過他的自傳而瞭解到他最為得意的《有限維向量空間》並開始閲讀,此後就成了他的忠實信徒,並且不自覺地逐漸追隨他的腳步,嘗試數學寫作。終於在十年後的今天,我可以寫他——我的引路人哈爾莫斯。如果十年前還是本科生的我能夠像現在這樣有想法,我會寫信告訴彼時還健在的他:親愛的哈爾莫斯教授,我是多麼地喜歡您的《有限維向量空間》!
致謝
在寫作過程中,作者得到香港城市大學的陳關榮教授、台灣國立交通大學的吳培元教授、美國南密西西比大學的丁玖教授、香港科技大學李健賢教授、 浙江省永嘉縣永臨中學的葉盧慶老師、美國勞倫斯伯克利國家實驗室邵美悦博士、重慶大學的邵紅亮博士、中國傳媒大學的陳見柯博士、上海大學的林明華博士和西北農林科技大學的汪逾淋同學的批評指正和有價值的建議,特表感謝!
參考文獻
[1] Halmos, I Want to Be a Mathematician– Automathography, Springer-Verlag,1985. 中譯本《我要作數學家》,馬元德、沈永歡、胡作玄、趙慧琪譯,江西教育出版社,1999年。
[2] Halmos, I Have a Photographic Memory. Mathematical Association of America, 1987.
[3] Halmos, 《測度論》,王建華譯,科學出版社,1958年
[4] Halmos,《希爾伯特空間問題集》,林辰譯,上海科技出版社,1984年
[5] Halmos, Linear Algebra Problem Book, Mathematical Association of America, 1995.
[6] Halmos, Problems for Mathematicians, Young and Old, Mathematical Association of America, 1991.
[7] J. H. Ewing, W. H. Gustafson, P. R. Halmos, S. H. Moolgavkar, W. H. Wheeler, and W. P. Ziemer, American mathematics from 1940 to the day before yesterday 中譯文《1940年以來的美國數學》,程其襄、張奠宙、應制夷 譯,《世界科學》1978年第1期,18–32.
[8] Halmos,The Heart of Mathematics, 中譯文《數學的心臟》,彌靜譯,《數學通報》1982年第4期,27–31.
[9] Halmos, Halmos講矩陣逼近(http://w3.math.sinica.edu.tw/mathmedia/pdf_a.jsp?m_file=ZDE2My8xNjMwNQ== “Halmos講矩陣逼近”),方資求筆錄,吳培元整理,《數學傳播》第十六卷(1992年)第三期, 1–10.
[10] Halmos, The teaching of problem solving, 中譯文可見《數學譯林》第9卷(1990年)第3期,256頁。
[11] Halmos, How to write mathematics,中譯文可見《數學譯林》第2卷(1983年)第2期,85頁。
[12] Halmos, How to talk mathematics,中譯文可見《數學譯林》第9卷(1990年)第4期,438頁。
本文經授權轉載自微信公眾號“數學與人文”。本文根據作者最新稿件進行編輯。
特 別 提 示
1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閲不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回覆四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。