你真的會解方程嗎？_風聞

你真的會解方程嗎？今天我們從簡單的解方程開始，為大家介紹一位英年早逝的數學家的工作，從這些工作中我們將看到優美的對稱性，以及藴含在其中的和諧奧妙。

撰文 | Marianne Freiberger

翻譯 | Nothing

審校 | C&C

尼爾斯·亨裏克·阿貝爾

1824年，一位年輕的挪威數學家尼爾斯·亨裏克·阿貝爾取得了一個與某類方程相關的令人震驚的結果。不久之後，法國天才數學家埃瓦里斯特·伽羅瓦以深入的眼光證明了這一結果為什麼是正確的——並在這個過程中開創了用數學研究對稱性的先河。可惜兩人都英年早逝，沒有來得及享受他們的工作帶來的好處。阿貝爾於1829年死於肺結核和貧困，時年26歲。伽羅瓦死於1832年，他在一場據稱是為了爭奪一個女人而進行的決鬥中被殺死。當時他只有二十歲。

那麼他們做出了什麼樣的工作？方程和對稱性又有什麼關係？

解方程

Solving Equations

最著名的公式之一是二次方程的通解公式，如果方程寫為：

雖然關於二次，三次，四次方程的通解公式看起來有些複雜，但是它們只包含了有限個運算操作：加、減、乘、除、開平方、開三次方、開四次方。

很顯然，你接下來會問，我們可以為五次方程找到一個類似的通解公式嗎？

更一般的，包含x高階項的多項式方程的通解公式長什麼樣子？

伽羅瓦畫像 在他死後16年的1848年，由他的兄弟根據記憶所作

我們想要的是一個公式，這個公式只包含加減乘除和求根操作。如果一個方程具有這樣一個通解公式，那麼我們説這個方程是有根式解的。

1824年阿貝爾證明的結論是：對於一般的五次方程，不存在根式解。當然，這並不意味所有的五次方程都是沒有根式解的。例如，多項式方程：

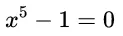擁有一個解：

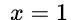但是對於一般的五次方程，確實不存在一個普適的根式解公式。

阿貝爾證明了這一結果，但幾年後，伽羅瓦才真正意識到為什麼五次方程不存在根式解。伽羅瓦常被認為羣論的奠基人，羣論是一門研究對稱性的數學。 我們通常認為對稱性是一種視覺現象：一幅畫或圖案可能是對稱的。但是對稱性和方程有什麼關係呢？答案有些微妙，但非常美麗。

不變的對稱性

Unchanging Symmetry

首先，讓我們思考對稱性真正的含義。我們説一個正方形是對稱的是因為我們將它繞着中心軸旋轉90度，或者將它對於各種軸做反射操作並不會改變它的外觀。所以對稱性意味着沒有變化：如果我們對某個物體進行某種操作之後並沒有改變它，那麼它就具有對稱性。

當我們思考二次方程式，我們可以發現少許對稱性。例如，二次方程

擁有兩個解

方程具有兩個離散的解，但是某種意義上，它們非常相似：只需在一個解上加上一個負號就可以得到另一個解。也許交換兩個解並不會帶來什麼不同，就像對正方形做鏡像操作一樣意味着一種對稱性一樣，交換方程的兩個解也許也意味着某種對稱性。但究竟是哪種對稱性呢？

加入無理數

Including Irrationals

蝴蝶有對稱性，方程也有對稱性！

為了理解這些結果，讓我們考察一下方程所包含的數字：

交換兩個解

Switching Solutions

伽羅瓦羣

Galois’s Group

為什麼你解不出一般的五次方程？

Why you can’t solve the general quintic?

我們可以對其他任意多項式做類似的事情，例如對一個五次方程：

紀念伽羅瓦的法國郵票

伽羅瓦所能證明的是，一個方程是否有根式解，取決於它的伽羅瓦羣的結構。有時候伽羅瓦羣可以被分成更小的分量，它們和取n次方根有關。如果是這種情況，那麼方程擁有根式解。

然而，如果它無法以恰當的方式分被解成更小的分量，如果你不能把對稱性分離出來，那麼你就找不到一個只涉及加、減、乘、除和求根的通解，在這種情況下，方程不存在根式解。

我們可以證明，五次方程並不能以恰當的方式分解。因此，五次方程不存在根式通解。對於包含x的更高次冪的多項式方程也是一樣的：它們沒有根式通解。用羣論研究方程的解被稱為伽羅瓦理論，這一理論以其發明者的名字命名。

本文經授權轉載自微信公眾號“中科院物理所”。

原文鏈接：https://plus.maths.org/content/stubborn-equations