相變點的演生對稱:物理常識今獲數學嚴格證明_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2021-07-18 10:21
一個物理系統中的相變可以是連續的,如鐵磁相變,或者是不連續的,如氣液相變。一個連續相變點的長程性質可以有比原系統更高的對稱性,這被稱之為演生對稱。如果原系統沒有連續旋轉對稱性,只有180度旋轉對稱性,那麼連續相變點也只有180度旋轉對稱性。可如果原系統有90度旋轉對稱性,那麼連續相變點就有可能有更大的連續旋轉對稱性。我們對連續相變點的演生對稱性有很好的物理理解,但數學上的嚴格證明還是很困難的。今天這篇文章介紹了這方面的一個最新進展。
——文小剛
撰文 | 潘佳棟
審校 | 劉培源
50多年來,數學家一直在尋找一種嚴謹的方法來證明對稱性在物理系統從一種狀態轉變為另一種狀態時是普遍存在的。被稱為共形不變性(conformal invariance)的對稱性,實際上包含三個獨立的對稱性。
現在,在2020年12月發佈的證明[1]中,一個由五名數學家組成的團隊更接近證明出共形不變性是物理系統在相變時的必要特徵。這項工作確定了旋轉不變性(共形不變性中三個對稱性之一)存在於各種物理系統的相變邊緣上。
以色列魏茨曼科學研究所的加迪·科茲馬(Gady Kozma)[2]説:“這是一項重大貢獻,它已經發布了很長時間。”

旋轉不變性是圓表現出的對稱性。將圓旋轉任意度數,它看起來都一樣。這意味着在處於相變邊緣的物理系統中,無論系統模型如何旋轉,系統都可以表現出一些相同的屬性。
早期的結果已經證明旋轉不變性適用於兩個特定模型,但他們的方法不夠靈活,無法應用於其他模型。 新的證明標誌着旋轉不變性是一系列模型中的普遍現象。
法國高等科學研究所 (IHES) 和日內瓦大學的雨果·杜米尼爾·科平(Hugo Duminil-Copin)[3]説:“這種普遍性結果更加有趣”,因為這意味着無論物理系統模型之間有什麼差異,都會出現相同的現象。
杜米尼爾·科平與里昂高等師範學院的卡羅爾·卡傑坦·科茲洛夫斯基(Karol Kajetan Kozlowski)[4]、日內瓦大學的德米特里·克拉春(Dmitry Krachun)、弗裏堡大學的伊昂·馬諾萊斯庫(Ioan Manolescu)[5]以及IHES和巴黎薩克雷大學的Mendes Oulamara[6]是這項工作的合作者。
這項新工作帶來了新的希望,數學家們可能正在接近一個更加宏大的結果:這些物理模型是共形不變的。 在過去的幾十年裏,數學家已經證明了共形不變性適用於一些特定的模型,但他們一直無法證明它適用於所有模型。這個新的證明為獲得全面的結果奠定了基礎。
日內瓦大學的斯坦尼斯拉夫·斯米爾諾夫(Stanislav Smirnov)[7]説:“這是一個非常大的突破,共形不變性現在看起來觸手可及。”
1. 神奇的時刻
一種狀態和另一種狀態之間的轉換是自然界中一些最令人着迷的事件。 有些是突然的,比如水加熱成蒸汽或冷卻成冰時的轉變。其他的,比如在新工作中研究的相變,它在兩種狀態之間有一個模糊的邊界。正是在這些臨界點,系統處在過渡狀態。
數學家們試圖用簡化的模型來抑制這種現象。
舉個例子,當你加熱鐵時,當它超過一定温度,它會失去磁性。這種變化發生在數以百萬計的原子作為微型磁鐵翻轉並且不再與它們鄰居的磁性位置對齊時。大約1000華氏度,熱效應獲得勝利,磁鐵就變成了一塊金屬。
數學家用伊辛模型[8]研究這個過程。它將一個鐵塊想象成一個二維方形格子,很像一張方格紙上的網格。 該模型將鐵原子置於晶格線的交點處,並將它們表示為向上或向下的箭頭。
伊辛模型在1950年代被廣泛用作表示臨界點附近物理系統的工具。這包括失去磁性的金屬、空氣中的汽液轉變和金屬有序和無序之間的轉換。這些都是不同類型的系統,它們在微觀層面上以不同的方式運行。
然後,在1970年,年輕的物理學家亞歷山大·波利亞科夫( Alexander Polyakov)[9]預測[10],儘管這些系統存在明顯差異,但這些系統在其臨界點都表現出共形不變性。經過數十年的分析,物理學家相信波利亞科夫是對的,但是數學家們面對着嚴格證明的艱鉅工作。
2. 對稱性的對稱性
共形不變性由三種類型的對稱性組成,它們共同組成一種更廣泛的對稱性。研究人員可以移動物體(平移對稱),將它們旋轉任意度數(旋轉對稱),或更改它們的大小(標度對稱),所有這些都不會改變它們的任何角度。
杜米尼爾·科平(Duminil-Copin)説:“對於共形不變性,有時我稱之為‘統治對稱性的對稱性’,這是因為它是一種整體對稱性,比其他三種對稱性更強。”
共形不變性以更微妙的方式出現在物理模型中。在伊辛模型中,當磁性仍然完整且尚未發生相變時,大多數箭頭的指向可以形成巨大的原子團。 還有一些小原子團,其中所有箭頭都指向下方。但是在臨界温度下,原子可以以更遠的距離相互影響。在臨界點,各處的原子排列都變得不穩定:大小不一、箭頭朝上或朝下的原子團同時出現,磁性臨近消失。
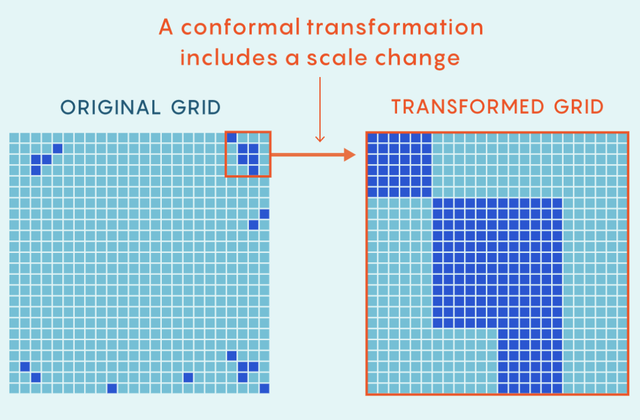
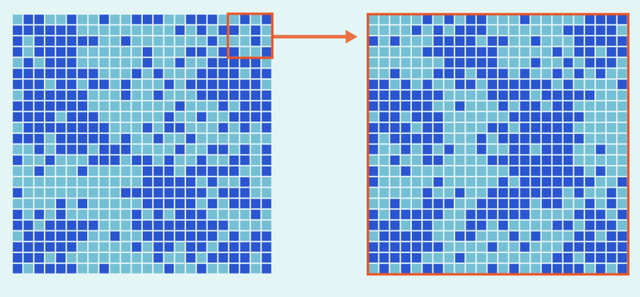
在這個臨界點,數學家觀察模型並研究箭頭之間的相關性,這表示了給定一對格點指向同一方向的可能性。在此設置中,共形不變性意味着可以平移、旋轉和縮放網格,而不會改變這些相關性。也就是説,如果兩個箭頭有50%的機會指向同一方向,然後使用這些對稱性,那麼在晶格中佔據相同位置的箭頭也有50%的機會對齊。
結果是,如果將原始晶格模型與變換後晶格模型進行比較,將無法分辨原來的和新的模型。重要的是,相變之前的伊辛模型並不是這樣的。在那裏,如果將格子的頂角調整為與原始大小相同的大小,這將增加向下箭頭原子團的大小,從而很明顯得到哪個格子是原來的。
共形不變性具有直接的物理意義:它表明即使調整物質的微觀細節,系統的全局行為也不會改變。 它還暗示了某種優雅的數學,就像整個系統正在打破其總體形式併成為其他東西一樣。
3. 第一個證明
2001 年,斯米爾諾夫提出了物理模型中共形不變性的第一個嚴格數學證明[11]。 它適用於滲流模型,即液體在多孔介質(如石頭)中穿過的過程。
斯米爾諾夫研究了三角形格子上的滲透,其中水只能流過“開放”的頂點。最初,每個頂點對水流開放的概率相同。 當概率較低時,水流穿過石頭的可能性較低。
但是隨着研究人員慢慢增加概率,會出現一個點,有足夠多的頂點打開以創建穿越石頭的第一條路徑。斯米爾諾夫證明,在臨界點處,三角形晶格是共形不變的,這意味着無論如何使用共形對稱對其進行變換,都會發生滲流。
五年後,斯米爾諾夫在2006年的國際數學家大會上宣佈他證明了共形不變性[12],這一次是在伊辛模型中。結合他2001年的證明,這項工作為他贏得了數學界的最高榮譽“菲爾茲獎”。
從那以後的幾年裏,研究人員提出了一些其他證明,為一些特定模型建立了共形不變性,但是沒有人能夠證明波利亞科夫所設想的共形不變性的普遍性。
紐約大學阿布扎比分校的數學物理學家費德里科·卡米亞(Federico Camia)[13]説:“之前的證明是針對特定模型的。你需要有一個非常具體的工具來證明一個非常具體的模型。”
斯米爾諾夫本人承認,他的兩個證明都依賴於他使用的兩個模型中存在但通常不可用的某種“魔法”。他説,“這項新工作是第一個打破這種模式的工作——它證明了旋轉不變性,這是共形不變性的核心特徵,在物理模型中廣泛存在。”
4. 一次一個
杜米尼爾·科平在2000年代後期首次開始考慮證明共形不變性的普遍性,他當時還是斯米爾諾夫在日內瓦大學的研究生。 他對導師證明的輝煌以及他們的侷限性有着獨特的理解。 斯米爾諾夫繞過了分別證明所有三個對稱性的需要,而是找到了建立共形不變性的直接途徑——就像通往山頂的捷徑一樣。
“他是一個了不起的問題解決者。 他在這座巨大的山上找到入口,證明了兩種統計物理學模型的共形不變性,就像他經過難點一樣。”杜米尼爾·科平説。
在研究生畢業後的幾年裏,杜米尼爾·科平致力於提出新的證明。當他和他的合作者開始認真研究共形不變性時,他們已經準備好採用與斯米爾諾夫不同的方法。他們沒有用魔法冒險,而是回到了波利亞科夫和後來的物理學家提出的共形不變性的最初假設。

物理學家需要分三個步驟進行證明,共性不變性都存在對稱性:平移不變性、旋轉不變性和標度不變性,分別證明它們中的每一個就會得到共形不變性。考慮到這一點,研究人員首先着手證明標度不變性,他們認為旋轉不變性將是最困難的對稱性。在嘗試時,他們認識到他們可以證明在方形和矩形網格上的各種滲流模型的臨界點存在旋轉不變性。
他們使用了概率論中概率耦合(coupling)的方法,該方法可以直接比較方形晶格與旋轉矩形晶格的大規模演化行為。 通過將這種方法與另一個稱為可積系統領域的思想相結合,該領域研究演化系統中的隱藏結構,他們能夠證明模型中相變點的行為是相同的——從而建立旋轉不變性。之後他們證明了他們的結果可以擴展到其他物理模型。
最終結果證明了旋轉不變性是二維模型的普遍屬性。他們工作的成功表明,融合不同數學領域的類似方法對於在共形不變性方面取得進一步的研究進展是必要的。
“我認為,在共形不變性的論證和相變研究中,你需要一點點證明。你不能只從一個角度來證明它。”杜米尼爾·科平説。
5. 最後的步驟
自斯米爾諾夫2001年的證明以來,數學家第一次對證明共形不變性的普遍性有了新的認識。 與早期的工作不同,這個新結果開闢了新的方法。通過使用遵循自下而上的方法,他們希望一次證明一個組成部分的對稱性。
現在,隨着旋轉不變性被證明,杜米尼爾·科平和他的同事們將目光投向了標度不變性,這是他們最初的目標。考慮到最近關於旋轉對稱的工作,標度不變性的證明將使數學家處於證明完全共形不變性的時刻,證明方法的靈活性使研究人員對其感到樂觀。
“我認為第三步很快就會被證明,”杜米尼爾·科平説。“如果不是我們,那就是更聰明的人,但我可以肯定這很快就會發生。”然而,旋轉不變性的證明耗費了五年時間,所以下一個結果可能還需要一些時間。 儘管如此,斯米爾諾夫還是希望共形不變性最終可以被證明。斯米爾諾夫説:“這可能需要一週時間,也可能需要五年,但我比11月時樂觀得多。”
參考文獻
[1]https://arxiv.org/abs/2012.11672
[2]http://www.wisdom.weizmann.ac.il/profile/scientists/kozma-profile.html
[3]https://www.ihes.fr/en/professeur/hugo-duminil-copin-2/
[4]http://www.ens-lyon.fr/PHYSIQUE/presentation/annuaire/kozlowski-karol
[5]https://homeweb.unifr.ch/manolesc/Pub/
[6]https://www.ihes.fr/~oulamara/
[7]http://www.unige.ch/~smirnov/
[8]https://www.quantamagazine.org/the-cartoon-picture-of-magnets-that-has-transformed-science-20200624/
[9]https://phy.princeton.edu/people/alexander-polyakov
[10]http://jetpletters.ru/cgi-bin/articles/download.cgi/1737/article_26381.pdf
[11]https://arxiv.org/abs/0909.4499
[12]https://www.unige.ch/~smirnov/papers/icm-publ.pdf
[13]https://nyuad.nyu.edu/en/academics/divisions/science/faculty/federico-camia.html
本文經授權轉載自微信公眾號“集智俱樂部”,原標題為《數學家證明相變的對稱性:從旋轉對稱性到標度不變性》。原文鏈接:
https://www.quantamagazine.org/mathematicians-prove-symmetry-of-phase-transitions-20210708/