Kitaev 模型材料α -RuCl 3中的近似鐵磁_風聞

抽象的

α -RuCl 3是實現 Kitaev 量子自旋液體的主要候選者，但其在低温下的鋸齒形反鐵磁有序表明與 Kitaev 模型存在偏差。我們通過在 Ru L3處的共振非彈性 X 射線散射研究量化了α -RuCl 3的自旋哈密頓量吸收邊。在順磁狀態下，磁激勵的準彈性強度在區域中心周圍具有廣泛的最大值，而在鋸齒形磁布拉格波矢處沒有任何局部最大值。這一發現意味着鋸齒形順序是脆弱的，並且很容易被競爭的鐵磁相關性破壞。實驗確定的哈密頓量的經典基態實際上是鐵磁性的。之字形狀態通過量子漲落而穩定，留下鐵磁性——連同基塔耶夫自旋液體——在能量上接近亞穩態。這三個密切競爭的狀態及其集體激發是對磁場中α -RuCl 3的不尋常性質的理論理解的關鍵。

介紹

量子自旋液體狀態的特點是大程度的糾纏支持分級準粒子1 , 2。由於其精確的溶解度和量子自旋液體基態，蜂窩晶格3上的 Kitaev 模型近年來一直是研究的中心焦點。值得注意的是，存在磁場時的基本激發由湧現的非阿貝爾任意子表示，這可以作為拓撲量子計算的關鍵元素。Kitaev 模型的鍵向磁相互作用可以在強相關的過渡金屬化合物中實現，其中自旋軌道糾纏的贗自旋[Math Processing Error]S~=1/2排列在共享邊緣的八面體的蜂窩晶格上4，5。由 Ir 4+或 Ru 3+離子組成的蜂窩狀晶格化合物是實驗實現 Kitaev 自旋液體6 , 7 , 8 的主要候選物，因為它們的[Math Processing Error]t2g5電子配置支持[Math Processing Error]S~=1/2在存在強自旋軌道耦合的情況下9 狀態。特別是，α -RuCl 3 (以下稱為 RuCl 3 ) 10，二維範德華磁性的典型例子11，由於大單晶的可用性和從剝離的納米片12合成功能器件的前景，一直是深入研究的焦點。

然而，大多數 Kitaev 候選材料在足夠低的温度下會發生磁性轉變。這主要是由非 Kitaev 最近鄰 (NN) 相互作用引起的，包括海森堡和非對角耦合13、14、15，它們源自離子之間的直接跳躍和來自其配位八面體的扭曲。真實材料中的額外相互作用需要對擴展的 Kitaev-Heisenberg Hamiltonian 進行分析，其參數空間中的理論相圖由各種磁性有序相主導。特別是在 RuCl 3 16 中實現的鋸齒形反鐵磁 (AFM) 狀態[Math Processing Error]S~=1/2中，在鄰近純Kitaev點寬的參數範圍預測14，15，17。長範圍海森堡相互作用趨向於進一步穩定鋸齒次序18，19，20，21，驅動系統從自旋-液相程。

儘管低温下真實材料的磁性有序，但 Kitaev 相互作用可以在動態自旋相關中表現出來。在純Kitaev模型，出射的準粒子的簽名出現在自旋動力學結構因子激發的連續體的形式22，23，24。在的RuCl 3，磁散射連續已經通過拉曼散射觀察到25個非彈性中子散射實驗26，27，28，29。此外，觀察到磁場中熱霍爾傳輸係數的半整數量化30支持將自旋分解為馬約拉納費米子。隨着在 RuCl 3 中Kitaev 相互作用的實驗證據越來越多，完全確定其贗自旋哈密頓量至關重要。一組連貫地解釋低温鋸齒形順序和分餾特徵的參數將建立一個具體的、可控的自旋液相途徑。這客觀上，然而，尚未實現，部分原因是不同的交互方面已經強調解釋套限量實驗數據，導致提出贗車型動物園31，32，33。

在目前的工作中，我們已經確定在的RuCl的贗哈密頓的首項3通過使用諧振無彈性x射線散射（RIXS）34，35在茹大號3吸收邊緣調查的RuCl的激發光譜3在寬光譜範圍。截面的共振增強使我們能夠以高統計量觀察高能激發 (>100 meV)，使我們能夠準確地確定立方晶體場分裂 10 D**q、洪德耦合JH和自旋軌道耦合常數λ; 然後將這些參數用於交換常數的理論評估。通過利用Ru L3吸收邊（2837.8 eV）處入射和出射光子之間的大動量轉移，我們繪製了低能橫跨整個第一布里淵區的流形。與 RIXS 強度的精確對角化計算的比較產生了贗自旋之間相互作用參數的層次結構並揭示了它們各自的作用：(1) 鐵磁 (FM) Kitaev 耦合K  = -5.0 meV 占主導地位，(2) FM Heisenberg 相互作用J[Math Processing Error]S~=1/2 = -3.0 meV 增強了 FM 相關性並使之字形順序變得脆弱，（3）非對角相互作用 Γ = 2.5 meV 在低温下穩定了之字形順序並解釋了磁矩方向。事實上，我們的實驗表明，鋸齒形和鐵磁態之間存在強烈的競爭，通過量子零點漲落解決了有利於前者的競爭，如圖1a所示 。以這種方式獲得的相互作用哈密頓量與我們從高能多重態的理論分析中獲得的相互作用非常吻合，從而為進一步研究 RuCl 3提供了堅實的基礎，包括對磁場中自旋液體行為的理論分析。更一般地説，我們確定低能量有效哈密頓量的綜合方法可以作為研究其他量子磁鐵和自旋液體候選物的藍圖。

圖 1：Ru L3邊緣 RIXS揭示的RuCl 3 中的相競爭和散射幾何。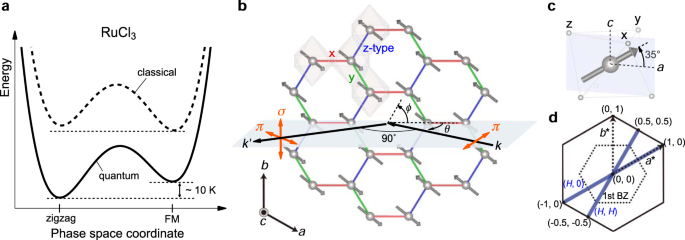a之字形基態附近的經典和量子能量圖譜示意圖。之字形順序通過量子效應穩定，並且僅比競爭性亞穩態鐵磁 (FM) 狀態的能量略低。b贗自旋-1/2矩（灰色箭頭）顯示了α -RuCl 3蜂窩晶格上的鋸齒形磁序模式。灰色陰影的 RuCl 6八面體共享三個不同的x、y和z型鍵的邊緣，分別由紅線、綠線和藍線表示。a、b和c表示晶格向量。具有動量k的入射 X 射線光子是線性π極化的，並且沒有分析具有動量的散射光子的極化。散射角固定在 90 ∘並且通過旋轉樣品角θ來改變面內動量傳遞q。方位角ϕ用於改變測量路徑。c RuCl 6八面體中的局部力矩方向。從中心 Ru 原子到相鄰的 Cl 原子的方向用x、y和z 表示[Math Processing Error]k′定義局部x、y和z座標軸。磁矩謊言內一個**Ç平面和點35 ∘從一個軸線68，53。在 RIXS 實驗中研究了d q  = ( H , 0) 和 ( H ,  H ) 路徑。虛線六邊形表示第一個布里淵區 (BZ)。

 結果晶體結構和散射幾何

圖 1（b）所示的晶體結構和曲折的RuCl的磁有序3，以及用於RIXS實驗散射幾何結構。為了便於與理論分析進行比較，我們將使用a  =  b  = 5.96 Å 和c  = 17.2 Å的六方晶體符號，其中a**b平面對應於蜂窩平面，c軸與其垂直。不同的x、y、z型鍵分別用紅線、綠線和藍線表示。入射 X 射線光子為π- 偏振，並且沒有分析散射光子的偏振。此後，動量傳遞用平面內分量q 表示，該分量通過旋轉樣本角度θ進行掃描。圖 1（c）所示的局部的定義XÿŽ座標和的RuCl內的局部磁矩方向6八面體。在下面的理論分析中，選擇贗自旋哈密頓量中的參數來重現力矩方向。圖 1 d示出了在所述測量路徑q -space研究在我們的實驗RIXS。我們沿着q  = ( H, 0) 和 ( H ,  H ) 方向，通過將方位角ϕ分別設置為 0° 和 -30°。q以倒格單位 (rlu) 表示。除非另有説明，測量是在 20 K 的基礎温度下在順磁狀態下進行的。

高能多重態圖 2提供了布里淵區中心 [ q  = (0, 0)] 在很寬的激發能量範圍內的 RIXS 光譜概覽。在約 1 eV 的電荷間隙（圖2 中的藍色虛線）上方出現並延伸至至少 4 eV的寬連續區 可以分配給位點間電子 - 空穴激發，這與光譜36和電子觀察到的連續區一致。能量損失光譜37。在位點連續體的頂部，觀察到主峯 B 和肩結構α、β和γ，它們被指定為從[Math Processing Error]t2g5基態到洪特多重內流形。在電荷間隙 (<1 eV) 以下，一個明顯的峯值 (A 1 ) 出現在 0.25 eV，它源於從基態雙峯到激發態四重奏。這種現象學建立了構成贗自旋哈密頓量的低能量雙峯的概念。我們將小肩結構 A 2歸因於A 1激子的倍數。光譜線形類似於 Ru M -edge RIXS 數據38[Math Processing Error]t2g4eg1[Math Processing Error]S~=1/2[Math Processing Error]S~=3/2[Math Processing Error]S~=1/2，但目前數據的更好統計允許從多重分析中精確確定微觀參數（補充説明 2）。

圖 2：從高能多重峯確定微觀參數。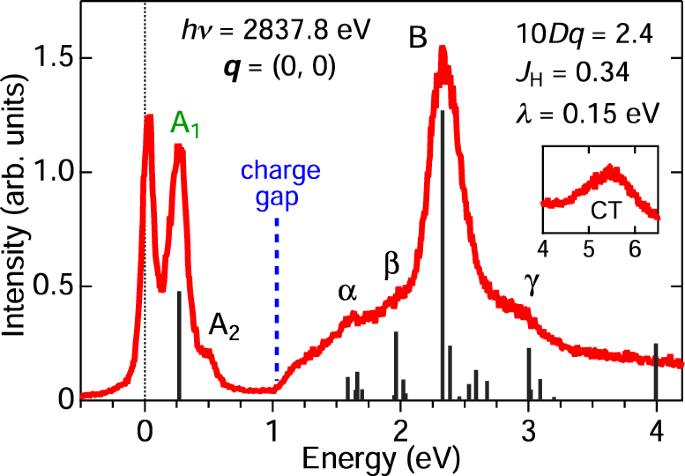RuCl 3在q  = (0, 0)處的代表性 Ru L3 RIXS 光譜，使用能量為 2837.8 eV 的光子拍攝。藍色虛線表示位點間電子-空穴連續體的起始能量。垂直黑條表示來自離子多重計算的理論 RIXS 強度（補充説明 2）。顯示了從 RIXS 光譜分析中獲得的立方晶體場分裂 (10 D**q )、洪德耦合 ( JH ) 和自旋軌道耦合 ( λ ) 參數。插圖顯示了包含p - d的高能量區域 電荷轉移 (CT) 激發。

全尺寸圖片具有最佳參數 10 D**q  = 2.4 eV、JH  = 0.34 eV 和λ  = 0.15 eV的理論 RIXS 強度顯示為圖2 中的豎線 。這些參數有較好的一致性與以前的報告10，36，38，39和下面將要用於量化交換常數。理論結果清楚地捕獲了位於 10 D**q 附近並分裂為JH函數的晶體場多重峯（B、α、β和γ）的峯值能量和強度，以及位於 ~3 λ /2處的轉換 (A 1 ) 。請注意，A 1峯沒有明顯的分裂。這與在蜂窩狀銥酸鹽 A 2 IrO 3 (A = Na, Li) 40 中觀察到的清晰的三角晶體場分裂形成對比，並表明 RuCl 3中的三角場分裂小於~0.1 eV 的實驗能量分辨率. 實際上，通過對磁化率各向異性的分析，我們獲得了四重分裂，僅為≃ 30 meV（補充説明4）。[Math Processing Error]S~=3/2[Math Processing Error]S~=3/2

自旋軌道激子和準彈性峯圖 3顯示了原始 RIXS 光譜在低能量範圍內沿q  = ( H , 0) 和 ( H ,  H ) 方向的動量依賴性。強度從H  < 0（掠入射）到H  > 0（掠射出口）的整體單調下降是由於 X 射線自吸收41的幾何效應，這將在以下定量強度分析中得到解釋。A 1峯顯示沿 ( H , 0) 和 ( H ,  H ) 方向沒有能量色散，表明[Math Processing Error]S~=3/2激子。值得注意的是，在T  = 20 K 時，準彈性峯值強度在鋸齒形磁布拉格波矢q  = (±0.5, 0)處沒有顯示任何局部最大值，表明當磁長程有序時，短程鋸齒形相關性被迅速抑制在TN  = 7 K 時消失。這一觀察結果與Na 2 IrO 3 42 , 43中遠高於TN的穩健的鋸齒形相關性形成鮮明對比。這一發現表明，RuCl 3的能量景觀在鋸齒形有序狀態周圍只有淺的最小值（圖 1a)，並且具有特徵向量q  ~ 0 的緊密競爭態，例如鐵磁態，作為亞穩態存在，其能量為kB TN  ~ 1 meV量級。該能量標度與約 8 T 磁場下的塞曼能量大致一致，其中之字形順序消失44和場誘導量子自旋液體的特徵出現29、45、46。[Math Processing Error]S~=1/2

圖 3：低能 RIXS 光譜的動量依賴性。a , b T  = 20 K 沿q  = ( H , 0) 和 ( H ,  H ) 方向的低能 Ru L3 RIXS 光譜。插圖顯示了q空間中的測量路徑。

 為了對 RIXS 光譜進行定量分析，我們按照 Minola 等人所述的程序校正了原始 RIXS 強度以應對 X 射線自吸收的影響。41（詳見補充説明 5）。圖 4 a、b 顯示了沿q  = ( H , 0) 和 ( H ,  H ) 方向的代表性校正光譜。我們將這些光譜分解為三個 Voigt 剖面，代表準彈性散射（藍色）、激子（綠色）和多激子（黑色虛線）。此處，Voigt 輪廓的高斯半峯全寬 (FWHM) 固定為 0.1 eV 的能量分辨率。[Math Processing Error]S~=3/2

圖 4：A 1峯和激發的FWHM 和強度。[Math Processing Error]S~=1/2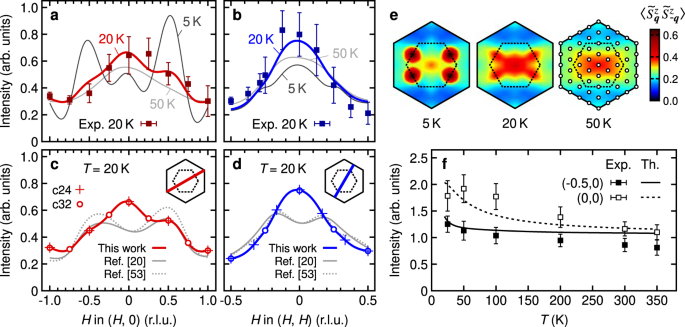a , b理論 RIXS 強度的動量依賴性在T  = 5 K（虛線）、20 K（實心藍色）和 50 K（實心青色）下計算，使用贗自旋哈密頓量 [方程。( 1 )]。為了獲得與實驗數據（平方）的最佳擬合，交換參數K  = -5, J  = -3, Γ = 2.5,和使用了 J3  = 0.75 meV。c , d比較使用不同參數集計算的 RIXS 強度。最佳理論曲線與參考文獻中提出的參數集的理論曲線進行了比較。 20和53[Math Processing Error]Γ′=0.1. 插圖顯示了q條路徑。這些點表示用於構建平滑輪廓的 24 位點簇（交叉）和 32 位點簇（圓圈）的可訪問q向量的結果。e等時贗自旋相關函數的温度演化為最優參數集。這些地圖是針對 32 站點集羣計算的，可訪問的q向量（圓圈）標記在 50 K 地圖上。f在q  = (0, 0) 和 (-0.5, 0)處 RIXS 強度的温度依賴性。數據點是用φ的方位角收集的[Math Processing Error]⟨S~qzS~−qz⟩ = 0 [( H , 0) 路徑的幾何形狀]。這些線顯示了通過模擬 24 站點集羣獲得的理論曲線。

全尺寸圖片準彈性強度和交換常數的動量依賴性圖 5 a、b 分別顯示了沿q  = ( H , 0) 和 ( H ,  H ) 方向的強度數據，以及在多個温度下計算的理論曲線對於最優參數集K  = -5, J  = -3, Γ = 2.5,和J3  = 0.75 meV。理論曲線是通過插入 24 和 32 位點簇的原始數據點生成的 [見圖 5 c、d]。觀察到的q[Math Processing Error]S~=1/2[Math Processing Error]Γ′=0.1我們的計算很好地再現了 20 K 時 RIXS 強度的依賴性，特別是包括 (0, 0) 處的強度最大值和沿 ( H ,  H ) 方向的更清晰的強度分佈。請注意，在 5 K 處計算的 ( H , 0) 方向的理論曲線在q  = (±0.5, 0)處具有明顯的峯值，對應於在TN  ≃  7 K處設置的鋸齒形磁序。 然而，這些峯值很快在 20 K 時消失，導致 RIXS 強度沒有局部最大值，而光譜的其他區域僅顯示逐漸修改。

在證明了我們的理論方法對 RIXS 強度的能力後，我們將我們的方法應用於文獻中的其他模型以測試它們的有效性。圖 5 c、d 顯示了不同參數集在 20 K 時的理論 RIXS 強度的比較。具體來説，我們比較我們的模型與 Winter 等人的。20 (-5, -0.5, 2.5, 0, 0.5) 和 Sears 等人的模型 2。53[Math Processing Error](K,J,Γ,Γ′,J3)=(−5,−3,2.5,0.1,0.75)(-10, -1.5, 8.8, 0, 0.4) meV。與我們的數據相反，文獻中的兩個模型表明，全局最大值不在 (0, 0) 附近，而是停留在磁布拉格波矢 (±0.5, 0) 附近。因此，Γ 點附近的實驗強度最大值突出了增強的 FM 相關性，我們將其歸因於大 FM Heisenberg 相互作用J  = -3 meV ~  K /2（與J / K  = 0.1 20和 0.15 53 相比）。該比較表明 RIXS 強度的動量依賴性對模型參數高度敏感。雖然它們受到一定的變化（例如，通過包括在層間聯軸器54，55在擬閤中），上面獲得的整體層次結構是穩健的，正如 由 FM Kitaev 和 FM Heisenberg 耦合支持的q ~ 0 相關性與鋸齒形順序密切競爭並在T  ~ 20 K 時變得突出的條件所決定的.基於對低能磁激勵的分析，最近的理論著作33 , 56也指出了與 FM 的接近性。

我們注意到接近 FM 狀態對 RuCl 3的理論描述具有重要意義。表 1顯示了幾種模型中 FM 狀態的經典能量（相對於鋸齒相的能量）。與參考模型相反。 如圖 20和53 所示，我們的 RIXS 衍生模型中的鐵磁態實際上比經典水平上的鋸齒狀狀態的能量 (-0.12 meV) 低，如圖 1a 所示。因此，鋸齒形順序的穩定歸因於強量子漲落，這是高度受挫的 Kitaev 相互作用所固有的，並在我們的精確對角化分析中得到了充分考慮。這一觀察結果使 RuCl 中鋸齒形順序的經典處理無效3基於例如標準線性自旋波理論。相反，必須從一開始就考慮量子零點漲落，以獲得穩定的鋸齒形順序並正確描述其激發。考慮到鐵磁磁振子的非平凡拓撲結構，鋸齒形順序的量子起源和與 FM 狀態的接近性對於理解 RuCl 3 26 , 27 , 28 , 29 中的異常中子散射連續譜及其場致特性是必不可少的在Kitaev材料57，58。

  典型模型參數的鐵磁態相對於鋸齒形的經典能量（所有能量均以 meV 為單位）。全尺寸表為了進一步形象化我們的模型的特性，我們繪製在圖 5的等時間贗相關函數電子強度映射對於T  = 5 K、20 K 和 50 K。地圖是從 32 個站點的集羣生成的，可訪問q[Math Processing Error]⟨S~qzS~−qz⟩矢量（圓圈）標記在 50 K 地圖上。在 5 K 時，系統處於鋸齒形有序相位，頻譜權重集中在磁布拉格波矢周圍，但從 (0, 0) 附近的強度也可以看出相當大的 FM 相關性。隨着之字形長程階數消失，布拉格波矢處的頻譜權重迅速轉移到 (0, 0) 附近，反映了由於 FM Kitaev 和 Heisenberg 相互作用而產生的明顯 FM 相關性 [ T  = 20 K 圖 5 e ]。在T  = 50 K 時，強度分佈完全由 Kitaev 項主導，類似於純 FM Kitaev 模型的強度分佈。為了進一步證明我們模型的預測能力，我們在圖 5 中顯示f 在q  = (0, 0) 和 (-0.5, 0)處 RIXS 強度的温度依賴性。數據是在方位角φ  = 0 時收集的[即( H , 0) 路徑的幾何形狀]。與理論一致，q  = (0, 0) 和 (-0.5, 0)處的 RIXS 強度逐漸降低至 ~200 K 並在較高温度下收斂。值得注意的是，即使在T  = 100 K 時，q依賴性也明顯存在，表明遠高於TN 的贗自旋之間的強相關性。

K , J , Γ 和理論估計[Math Processing Error]Γ′實驗發現的 FM Kitaev 耦合的優勢與理論考慮4的 Hund 規則耦合JH對交換相互作用的影響是一致的。Γ 的可觀值可歸因於這樣一個事實，即 4 d軌道在空間上延伸，因此它們的直接重疊很大14。FM 符號相對較大的 ( J  ~  K /2) 海森堡耦合有點令人驚訝。它可能由interorbital支持噸2克- ë克hoppings 5，給定分裂立方體10 d**q[Math Processing Error]t′ 這裏比較小。

手頭有幾個微觀參數，如JH、10 D**q、Δ p**d和λ由上述 RIXS 數據量化，我們可以從理論上估計交換參數。特別地，我們想評估非對角線項（在上面的擬閤中被忽略）作為三角晶體場 Δ 的函數，看看它是否是對於 RuCl 3 來説，Δ 值確實很小。為此，我們按照以前的工作17，59，並考慮四種不同的NN交換機制：（1）間接跳牛逼的牛逼2克[Math Processing Error]Γ′電子通過中間 Cl 離子，（2）它們的直接 NN 跳躍，（3）電荷轉移和循環交換過程，涉及具有能量 Δ pd 的p**d電荷轉移激發，以及（4 )軌道間t2g - eg跳躍涉及Cl- p和 Ru- e-g軌道之間的強tpd**σ重疊。計算是標準但冗長的，詳細信息將在別處介紹。[Math Processing Error]t′

圖 6顯示了這些計算的結果作為三角晶體場 Δ 的函數，它控制着贗自旋波函數的形狀。在 Δ = 0 的三次極限中，消失並且J也很小，因此 NN 交換哈密頓量以K和 Γ為主。對於正 Δ，海森堡項J為正，Δ 較大時它變得與 Kitaev 相互作用相當，而 Γ 逐漸減小。觀察到的 FM J  < 0 和 RuCl 3 中相當大的 Γ 值清楚地表明該化合物中的 Δ 為負值。事實上，從我們對順磁化率的分析（見補充説明 4[Math Processing Error]Γ′=0)，我們得到了一個負值 Δ  ≃  −50 meV 和比率δ  = 2Δ/ λ ≃  − 0.7。在這個δ值，計算的交換常數為 meV（我們假設能量標度t2 / U≃  12 meV）。這些常數的符號和相對值與參數集 meV 從 RIXS 實驗推導出來。最重要的是，計算得到的[Math Processing Error](K,J,Γ,Γ′)≃(−5,−2.2,3.3,1.3) [數學處理錯誤] (鉀,J,Γ,Γ′)=(-5,-3,2.5,0.1)[數學處理錯誤]Γ′值確實是 NN 交換常數中最小的。該結果與最近對交換常數60 的ab-initio 估計一致。

圖 6：理論交換參數。 交換參數K（紅色）、J（黑色）、Γ（藍色）和（灰色）作為δ  = 2Δ/ λ的函數，使用以下公式計算10 D**q  = 2.4 eV，JH  = 0.34 eV， 從 RIXS 數據獲得的p**d電荷轉移間隙 Δ pd = 5.5 eV（圖 2）。我們使用庫侖相互作用的代表值U  = 2.5 eV 對於 Ru- d軌道，Up  = 1.5 eV 和 Hund 耦合Jp  = 0.7 eV 對於 Cl- p[數學處理錯誤]Γ′軌道，σ和π通道中p**d電荷轉移積分 之間的比率t**pdσ / t**pdπ = 2 ，以及直接t2 g跳躍。交換常數以t2 / U為單位給出。垂直灰線表示 適合於 RuCl 3 的δ ~ - 0.7 。[數學處理錯誤]噸′=0.4噸

 圖6 中顯示的交換參數的整體行為 對於d5 Ru 和 Ir 化合物是通用的。實際上，使用適用於銥酸鹽59、61的微觀參數，可以獲得類似的依賴關係K ( δ ) 等，J的符號變化接近三次極限δ  ~ 0。具體來説，對於具有正δ 的Na 2 IrO 3  ~ 0.75 49，計算給出一個 AFM和一個小的[數學處理錯誤]J～Γ～12|鉀|[數學處理錯誤]Γ′<0，與最近的 RIXS 數據43一致。因此，RuCl 3和Na 2 IrO 3之間的質的差異可以主要歸因於δ的符號變化，這導致J的符號變化。RuCl 3 中具有負δ的FM增強了FM 相關性並導致鋸齒形順序的脆弱性。另一方面，具有正δ 的Na 2 IrO 3 中的 AFM導致穩定的鋸齒形相關性高達 70 K 43[數學處理錯誤]J～12鉀[數學處理錯誤]J≃12|鉀|. 這些考慮突出了三角場作為 Kitaev 材料中磁性的有效控制參數。我們還指出了 4 d RuCl 3和一類基於 3 d鈷酸鹽62、63的新型 Kitaev 材料的類比。在蜂窩狀鈷酸鹽中，K和J也是 FM 符號，FM 狀態與鋸齒形順序64密切競爭；因此，鋸齒形 AFM 階次可以在小至~1T 65 的磁場中被抑制。

這裏值得注意的是，我們的計算假設了理想的六邊形對稱，即x、y和z型鍵上的交換耦合K、J等是相同的。雖然這是順磁相（我們的實驗進行的地方）的合理近似，但低於T**N 的鋸齒形排序預計會通過贗自旋晶格磁彈性耦合打破這種對稱性，導致z型鍵上的交換參數與x上的不同/ y鍵沿之字形方向（見圖 1）。這種耦合，這一直是儀器對於理解低能磁振子動力學中自旋-軌道莫特絕緣體的Sr 2的IrO 4 66，67，也應在的RuCl的AFM狀態重要3，值得進一步研究。

總之，我們通過Ru L3 -edge RIXS研究了Kitaev模型材料RuCl 3。從準彈性 RIXS 強度的動量依賴性及其理論分析，我們量化了贗自旋 1/2 哈密頓參數。FM Kitaev 項K  = -5 meV 被發現是最大的，但海森堡交換J  = -3 meV 和非對角線交換 Γ = 2.5 meV 也很重要。特別是，大的 FM 相互作用J對於解釋觀察到的TN以上短程鋸齒形相關性的快速抑制至關重要. 我們發現鋸齒形 AFM 階的能量僅略低於競爭狀態，並且q  ~ 0 相關性，對於 FM Kitaev 模型是典型的，並通過大型 FM Heisenberg 相互作用J  ~  K /2進一步增強，很快就會變得突出當温度略高於TN. 我們對能量接近 FM 狀態的觀察也解釋了小磁場對鋸齒形順序的快速抑制。由高度受挫的 Kitaev 耦合控制的亞穩態的精確性質仍然是一個有趣的開放問題。這些狀態的層次結構和它們之間的相互作用可能會受到哈密頓量中的子主導項的影響，這無法通過我們的測量和分析來精確確定，也可能受到我們沒有考慮的高階或層間相互作用的影響。

基於 從居里-魏斯分析確定的各向異性g因子gab  = -2.53 和g**c = -1.56，我們確定三角場分裂 Δ 為 ~-50 meV（對應於三角伸長率）。與自旋軌道耦合λ相比，相對較弱的三角分裂導致未淬滅的軌道矩並支持自旋軌道糾纏波函數的概念。使用 從 RIXS 光譜的高能多重峯推導出的微觀參數 10 D**q  = 2.4、JH  = 0.34 和λ = 0.15 eV，我們評估了交換常數[數學處理錯誤](鉀,J,Γ,Γ′)也在理論上，再現了實驗確定參數的符號和層次結構。值得注意的是，對於實驗相關的三角參數δ確實處於層次結構的底部，並且J作為δ的函數改變符號。在 RuCl 3 中以負δ獲得的 FM J是造成鋸齒形順序的脆性的原因，與其在具有正δ和 AFM J 的Na 2 IrO 3 中的穩定性遠高於T**N[數學處理錯誤]Γ′. 總的來説，我們的發現為未來 RuCl 3 的理論和實驗研究奠定了堅實的基礎。特別是，在q  ~ 0處觀察到的低能亞穩態，由受挫的基塔耶夫和海森堡相互作用控制，應該與對該材料不尋常的場誘導特性的定量理解有關。

為了確定 RuCl 3的交換哈密頓量，我們引入了一種綜合方法，該方法將來自 RIXS 數據的信息整合到非常廣泛的能量和動量範圍內。對這些光譜的雙管齊下的理論分析產生了一致的結果，激發了人們對相互作用參數的信心，作為對該材料未來研究的基礎。特別是，等時相關函數的系統計算使我們能夠將準彈性 RIXS 數據評估為真實空間中贗自旋相互作用的指紋。由於 RIXS 只需要特徵尺寸約 10μm 的小晶體，我們的方法有可能發展成為一種強大的篩選工具，用於快速擴展的 Kitaev 候選材料列表。

方法樣品生長和表徵

RuCl 3單晶是通過化學蒸汽傳輸生長的，如前所述12。在真空下將無水多晶 RuCl 3（99.9%，Acros Organics）密封在約 12 釐米長的石英安瓿中。將反應物以 3 K min -1的速率加熱至 1023 K 120 小時，然後自然冷卻至室温。該反應在安瓿的較冷端產生閃亮的黑色結晶片狀 RuCl 3。通過粉末X射線衍射和掃描電子顯微鏡以及能量色散X射線光譜分析產物以檢查晶體的純度。我們晶體的磁化率在 7 K 處顯示異常，對應於 Néel 温度 ( TÑ）之字形順序AFM的，但不顯示出任何異常現象在14ķ 12引起的堆垛層錯的非本徵磁轉變相關聯68，69。

IRIXS光譜儀的RuCl的RIXS光譜3使用新建成的中間體的X射線能量採集的RIXS分光計（IRIXS）在PETRA III，DESY動力學光束線P01 70，71，72。X 射線束聚焦到 20 μm × 150 μm (H × V) 的束斑上。使用 SiO 2 (10 ) 切塊球面分析儀和 CCD 相機以 90 ∘的散射角收集水平散射的光子，兩者都放置在羅蘭幾何中。零能量損失線的位置是通過測量沉積在樣品旁邊的銀漆的非共振光譜來確定的。IRIXS 光譜儀在 Ru L3處的總能量分辨率[數學處理錯誤]2¯-edge，定義為銀的非共振光譜的 FWHM，約為 100 meV。樣品上不同θ的 X 射線束足跡的變化不會影響我們檢測方案中的總強度。