關於糾纏的十四行詩｜量子多體中的吶喊與彷徨之十_風聞

撰文 | 孟子楊

來源 | 本文選自《物理》2021年第7期

十四行詩，英文叫Sonnet，老一輩翻譯家還曾根據音譯翻成商籟體，很好聽。其實是歐洲的格律詩，最初是小詩、小歌謠，也不一定十四行，隨着歷史的演進十四行詩句的格式逐漸被定型下來，而且押韻結構也有了嚴格的限制。在文藝復興時的意大利，有了彼特拉克體 (Petrarchan Sonnet)，音韻優美，以歌頌愛情為主。一般分為兩部分，前一部分由兩段四行詩組成，韻腳為a-b-b-a，a-b-b-a；後一部分由兩段三行詩組成，韻腳為c-d-e，c-d-e。後來流傳到英國，莎士比亞創作了大量的十四行詩 (其十四行詩集收錄154首，是莎翁全部作品中的重要一部分)，內容也從描寫愛情擴展到更加廣泛的領域，結構變成了三段四句加最後兩句，一般的韻腳為a-b-a-b，c-d-c-d，e-f-e-f，g-g，是為莎士比亞體 (Shakespearean Sonnet)。我們來舉一個實際的例子，下面是著名的莎翁十四行詩第18篇 (Sonnet 18)：Shall I compare thee to a summer′s day? (我能否將你比作夏天？)。

Shall I compare thee to a summer′s day?

Shall I compare thee to a summer′s day? (a)

Thou art more lovely and more temperate：(b)

Rough winds do shake the darling buds of May，(a)

And summer′s lease hath all too short a date；(b)

Sometime too hot the eye of heaven shines，(c)

And often is his gold complexion dimmed；(d)

And every fair from fair sometime declines，(c)

By chance, or nature′s changing course untrimmed：(d)

But thy eternal summer shall not fade，(e)

Nor lose possession of that fair thou ow′st；(f)

Nor shall Death brag thou wander′st in his shade，(e)

When in eternal lines to time thou grow′st：(f)

So long as men can breathe, or eyes can see，(g)

So long lives this, and this gives life to thee. (g)

我能否將你比作夏天？

我能否將你比作夏天？

你比夏天更加美麗温婉。

狂風將五月的蓓蕾凋殘，

夏日的勾留何其短暫？

休戀那麗日當空，

轉眼會雲霧迷濛。

休嘆那百花凋零，

摧折於無常的天命。

唯有你永恆的夏日常新，

你的美亦將毫髮無損。

死神也無緣將你幽閉，

你在我永恆的詩中長存。

只要一天有人類，或人有眼睛，

這詩將長存，並賜給你生命。

韻腳在每句後標明，大家可以反覆咀嚼體會，其實和中國的格律詩還有點模糊的相似。下面的中文翻譯是筆者從市面上幾家中湊出來的，儘量兼顧信和達，但還不夠雅，僅供參考。

雖然字面上還是寫愛情，如詩人將愛人比作夏天，寓意美麗和生命力的茂盛，但是也説出了夏天的不完美，也有狂風、驕陽、陰暗和結束的時候。任何美麗都會時過境遷，然而只要詩歌可以流傳，詩中的美——人類的精神創造，就可以在時間的長河裏不朽。這就超出了原本十四行詩只是情歌的範疇，討論起人的價值和人類創造的意義，從卿卿我我鴛鴦蝴蝶走向了人文主義的命題，是現代人的覺醒。

莎翁身後，十四行詩大行其道，一如老杜開創的律詩道路對中國後世詩人的影響。彌爾頓、華茲華斯、雪萊、濟慈、勃朗寧夫人，還有俄國的普希金、萊蒙托夫都創作出優秀的十四行詩，以至於普希金的詩體小説《葉甫蓋尼·奧涅金》就是用十四行的格律寫成，小説由四百多個十四行詩的單元組成，人稱“奧涅金詩節”，前無古人後無來者，一如戰鬥民族在其他領域 (比如物理學) 中的做事風格。

到了近代、現代，作為格律詩的十四行詩就像中國的律詩絕句一樣，慢慢被白話的自由體詩歌替代。但是還是有人創作不懈，如德語詩人里爾克和俄國的阿赫瑪託娃都有傳世之作，而且他們描寫的也是更加深沉和廣闊的主題，如前者的《致奧爾甫斯的十四行詩》(前後兩部共55首) 與後者的《海濱的十四行詩》。而正是里爾克的作品，對中國新詩人產生了極大的影響，這也就讓我們散漫的敍述又落到了中國，落到現代詩人、德國文學研究學者馮至身上。

1940—1941年間，詩人馮至經過了德國留學、回國工作，於抗戰中輾轉到昆明西南聯大教書。他從1920年代新文化運動時期的淺草社、晨鐘社，“我的寂寞是一條蛇”這樣略顯稚嫩的苦悶象徵中蜕化出來。在經歷了動盪年代的洗滌和近十年的沉默和思考之後，人到中年的詩人突然間被深沉的情感所喚起，爆發般地寫出了27首十四行詩，就是有名的《十四行集》。除了具有同時期宣傳愛國、痛訴苦難的作品 (如艾青、何其芳等人的) 的內容之外，馮至寫出一些更高的、更普遍也因此更動人的感受，所以就算撇開時代背景，在今天仍會觸動到我們內心深處的情感。這是詩人詩歌創作的巔峯之作，甚至可以説是“二十世紀上半葉中國詩歌創作的頂峯”。《十四行集》是馮至對生命的解答，而他給出的解答歸根結底是兩個字：孤獨。他用雕塑般的語言，用沉靜質樸的時空感受，完成了從幼嫩的白話詩到明晰的現代漢語詩的過渡。他的語言是適當歐化的白話，表現出具有現代性的感受力。不再囉嗦，還是抄一首做例子吧 (好在不用翻譯了)：

鼠尾草

我常常想到人的一生，

便不由得要向你祈禱。

你一叢白茸茸的小草

不曾辜負了一個名稱

但你躲避着一切名稱，

過一個渺小的生活，

不辜負高貴和潔白，

默默地成就你的死生。

一切的形容、一切喧囂

到你身邊，有的就凋落，

有的化成了你的靜默：

這是你偉大的驕傲

卻在你的否定裏完成。

我向你祈禱，為了人生。

這確實是現代漢語詩的高峯，不是古代的、也不是西洋的，而是新的、成熟的，描寫着現代人的情感和困惑的中文。

其實拉拉雜雜寫到此處，還沒有觸到這篇散漫文章的主題。也許這篇本來就沒有主題，就像馮至的十四行詩，“但願這些詩象一面風旗，把住一些把不住的事體”，只是在描述感受。那麼就讓我們按着如此的路數，接着描述筆者最近一段時間在量子多體糾纏中類似的感受吧。

諸君也許記得，我們在前文中討論過糾纏熵的秋褲量法 (參見：量子多體中的吶喊與彷徨之八：我愛糾纏如秋褲. 物理，2021，50(3)：199) 。但量子多體晶格模型糾纏的定量測量，還是一個新的領域。其背後的內容牽涉到量子糾纏應該用怎樣的數學語言來描述，怎樣在晶格模型中有效地進行計算，既關乎數學物理理論的進步也涉及量子多體計算技術的發展，需要兩相配合，才能達到有效探測量子多體糾纏這種與數學、物理學和信息科學都有關的新問題。

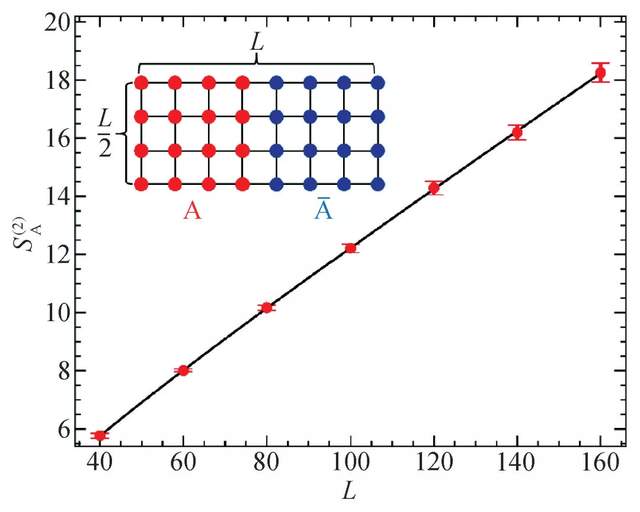
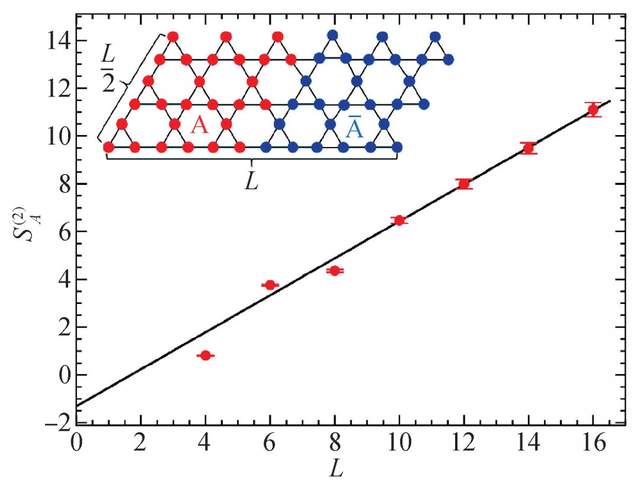
其中的一個主要想法，就是把量子多體系統放到有各種不同拓撲性質的流形上，然後把問題的配分函數和物理量在不同的時空流形上計算出來 (比如秋褲流形就是為了計算2階Renyi糾纏熵所設計的)，然後分析計算所得到系統的物理性質，比如糾纏熵隨着系統邊界面積的變化形式，從而得到糾纏熵的面積律和更加重要的——面積率後面的對數修正項和常數項。對數修正項的係數，或者常數項的數值，就反映了我們關心的量子多體系統的一些隱秘的但更加本質的性質。

如我們在前文中介紹的，在具有自旋旋轉對稱性自發破缺的反鐵磁奈爾態中，糾纏熵對數修正項前面的係數，就是系統中無能隙的戈德斯通 (Goldstone) 模式 (此處就是自旋波) 的數目 (圖1)；而在量子臨界點上的糾纏熵對數修正項的係數，就是如此相變共形場論描述中的中心荷 (central charge) 的值……糾纏熵的測量結果抓住了這些基本性質，就是抓住瞭如是量子多體系統的本質，超越了不同模型、不同量子材料繁複的化學、物理性質的表象。也正是因為能夠讓人們穿透量子多體系統指數增長的複雜性迷霧直抵問題的本質，糾纏熵——還有前文提到的無序算符等非局域測量——才吸引大家展開不懈的追尋。人們渴望能夠建立量子多體糾纏的內部結構——也就是大家經常看到的拓撲序這一個名稱——和流形的拓撲結構之間更加明確的關係，然後再通過切實可行的解析、數值計算方法，希望在量子多體晶格模型和更加複雜的實際材料中，把握糾纏，“把住一些把不住的事體”。

也只是在最近，事情才有了進展，筆者和合作者完善了糾纏熵的非平衡秋褲算法，通過引入非平衡做功的介觀物理概念和並行計算的程序實現 (細節此處從略了，解釋以待來日吧)，終於可以在有限的計算資源下比較可靠地得到2階Renyi在複雜的2維量子多體模型中的有限尺度標度關係，這是具有通用性的數值計算方法。

寫到此處，請允許筆者在本文中做最後一次跑題，跑回到十四行詩。馮至的《十四行集》中的最後一首“從一片氾濫無形的水裏” (不再抄了，感興趣的讀者可以自行查閲) 中有這樣的話，“但願這些詩象一面風旗，把住一些把不住的事體”。現代人的生活、我們面對的周邊和世界，紛繁蕪雜，又每每對我們施以略顯荒謬的挫折和羈絆，讓孤獨的個體常常感到苦悶、迷惑和看不懂生活的本質，一如孤獨的物理學者面對着現代的量子多體系統。但話説回來，我們這些渺小的個體仍想盡一己之力抓住一些生命中本質性的東西，能夠把自己的思、想安排在一個暫且穩定的流形之上，就是哲人們所説的——在存在與時間中詩意地棲居。從這個意義上講，從糾纏熵中看到對數修正的普適係數，看到拓撲序的普適簡併度，就和馮至的十四行詩一樣，讓我們從氾濫無形的水裏得到一個定形，用文字、用數學、用物理學、用計算，把住了一些把不住的事體。

本文經授權轉載自微信公眾號“中國物理學會期刊網”。

注：題圖為瑞士瓦萊的穆佐古堡，里爾克寫作《致奧爾甫斯的十四行詩》的地方。