Science封面文章解讀:花椰菜分形結構的起源_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2021-08-06 08:50

撰文 | 十三維
論文題目:
Cauliflower fractal forms arise from perturbations of floral gene networks View ORCID Profile
論文地址:
目錄:
1. 自然造化數學:從斐波那契數列到植物的葉序螺旋
2. 構建植物發育的 SALT 基因調控網絡
3. 形態動力學和GRN結合的多尺度生成模型
4.羅馬花椰菜花球的動態發展模型
5. 生物數學中斑圖動力學:形態發生學與基因調控網絡
在植物發育整個過程中,分生組織經常以確定的螺旋形、對生或輪生模式產生不同器官。花椰菜(Cauliflowers)呈現出一種不尋常的器官排列,在廣泛的尺度範圍內產生許多螺旋形的嵌套。這種分形的、自相似的組織是如何從發育機制中出現的,從古至今一直難以捉摸透。
最近一項結合對擬南芥花椰菜類突變體的實驗分析和建模研究發現,花球自相似性產生是因為分生組織未能形成花,但保留了它們在花狀態下短暫的“記憶”,並且在遞減的葉間期中不斷進行表達。
這項研究通過建立一個SALT基因調控網絡,並結合形態動力學參數,完整地解釋了羅馬花椰菜凝乳狀、具有明顯分形特徵的花球,是如何從分生組織發育程序和動態定義的關鍵參數中湧現出來的。
1 自然造化數學:從斐波那契數列到植物的葉序螺旋
不管植物學家是否懂得數學,但可以肯定的是,植物一定懂得數學。
例如,不同種類的花,花瓣數量是不一樣的,但卻並非是任意的。百合花有3個花瓣,毛莨花有5個,金雞菊通常有8個,瓜葉菊有13個,紫菀有21個,雛菊和向日葵通常有34、55、或89個,大型向日葵往往有144個花瓣——它們都符合著名的斐波那契數列:
Fn = Fn-1+Fn-2(n>=2), F0=0, F1=1
這個規律很少有意外,如果你發現少了,那很可能是因為一個花瓣掉落了。對於葉也一樣,人們常常憧憬去尋找傳説中象徵幸福的四葉草,也正因為這種三葉草的變異體極為稀少。

包括花葉在內的植物器官,都源自一種幹細胞池——莖尖分生組織 (SAMs) 的活動,由一種被稱為原基(primordium)的細胞團塊形成。人們很早就發現,葉在莖上的排列方式,即葉序的生長角度不是任意的,最常見的是相鄰偏差角總是137.5°的整數倍,對應週期分數的3/8。此外還有1/2、1/3、2/5、3/8、5/13……其組成同樣是斐波那契數列項,且比值越來越接近一個無理數——黃金分割比 ϕ=(1+√5)/2。
進一步研究發現,花數、葉序和果實的螺旋線在生長過程中所接近的角度就是 1/(1+ϕ),對應圓周角大約137.507764……°的值,它也被稱為黃金角度。原基在植物莖尖的生長規律如圖2所示,最終各個原基呈螺旋狀以黃金角度的倍數依次排開,形成了莖葉相間的奇特的幾何樣貌。

不要小看黃金角度的精確值,只有沿137.5°生長,才會形成圖3中間的費馬螺線。此外哪怕有十分之一的偏差,都會形成截然不同的結果[2]。在沿費馬螺線時,向日葵種子會緊密聚集在一起,中間沒有縫隙或重疊。此時種子充分利用了空間,堆積效率最高。

不僅角度,具有螺旋葉序的植物器官,還會通常形成兩個螺旋簇族(圖1A-C),以正反方向轉動,並出現在斐波那契數列的兩個連續數字中[1]。例如雛菊(圖4A)或向日葵花盤上的種子,逆時或順時針螺旋線的數量,往往都是8、13、21 或 34條。

而在花椰菜中,不僅一個尺度,在多個尺度上都可以看到凝乳狀的螺旋簇族(圖4D-F),每個花菜的小花球就像是由一個個微型版本的花菜組成的。這種組織自相似性在羅馬花椰菜(Romanesco)中達到了頂峯,其螺旋呈現類似於浮雕,在所有尺度上都是圓錐形,整個幾何外觀賦予了花球明顯的分形特徵(圖4G)。
如何解釋植物懂數學的現象?
維多利亞時代的科學家們信誓旦旦地認為,由於黃金分割是無理數,花葉的偏差角度或器官螺旋,讓空間利用效率最高,又能避免器官之間互相遮蓋,由此才能更有效地接收雨水和陽光生長。
但這種簡單解釋,就好像未卜先知地預設了植物們生長的目的,認為植物喜歡斐波那契數列或分形是原因一樣,卻並沒有給出「植物為什麼懂數學」的形成機制。答案當然不會這麼簡單。
最近,來自法國植物學家和數學家在 Nature上發佈的一項研究《Cauliflower fractal forms arise from perturbations of floral gene networks View ORCID Profile》,對通過研究擬南芥和花椰菜花球形成機制,建立了一個基於基因調控網絡 (GRN) 和形態動力學參數的模型,從分子層次解釋了調控羅馬花椰菜花球的形成具有明顯分形數學特徵的原因,對這一橫跨數百年的謎題給出了一個複雜但確切的回答。
2 構建植物發育的SALT基因調控網絡
花椰菜從捲心菜馴化而來,花序呈螺旋狀,每個新出現的花原基永遠不會成熟到花期,因此會不斷產生更多凝乳狀的花球[4, 5]。這種結構由十字花科擬南芥(Arabidopsis thaliana)的基因 AP1和CAL 雙突變引起(圖4H-I),是編碼MADS盒蛋白轉錄因子、促進花卉發育[8, 9]的兩個旁系同源基因。
控制擬南芥芽和花發育的基因調控網絡 (GRN) 已被大量研究,但能否夠解釋 AP1 CAL 突變尚不清楚[10-16]。在擬南芥中,花的發育由 LFY 啓動(圖5),LFY 由 SOC1 和 AGL24 兩種MADS盒蛋白,通過環境和內源性線索在整個花序分生組織中調控,並通過標記花分生組織起始位點的植物生長素最大值進行誘導,但它同時又被 TFL1 花序身份蛋白抑制。
此後在花原基中,LFY 誘導 AP1 和 CAL,同時它們也對 LFY 產生正反饋,並抑制SOC1/AGL24 和 TFL1,從而確保每個新分生組織的命運是成為一朵花。

但在 AP1 CAL突變體如花椰菜中,AP1/LFY 正反饋不存在,TFL1 不受產生花的分生組織中 AP1/CAL 的抑制。因此,幼花原基不能維持 LFY 表達並開始表達 TFL1。結果,它們失去了花朵身份而成為別樣花序的分生組織[8]。
TFL1 在新生花原基中的抑制在以往研究已理解,但直接導致它在 AP1 CAL 花序分生組織中上調的因素尚不清楚。作者通過搜索了除 LFY 之外的 TFL1 的直接正向調節因子,檢查了 SOC1 和 AGL24,通過功能性喪失和獲得實驗表明二者均誘導 TFL1(圖6A-I),染色質免疫沉澱 (ChIP) 也表明這兩個轉錄因子會與 TFL1 區域結合,調節分生組織中的表達[22](圖6J-L)。通過在過渡相試驗(transient assay)中構建 SOC1 和 AGL24,表明這些區域足以激活TFL1 併產生基因報告(圖6M&N),從而證實它們是 TFL1 的直接調節器。
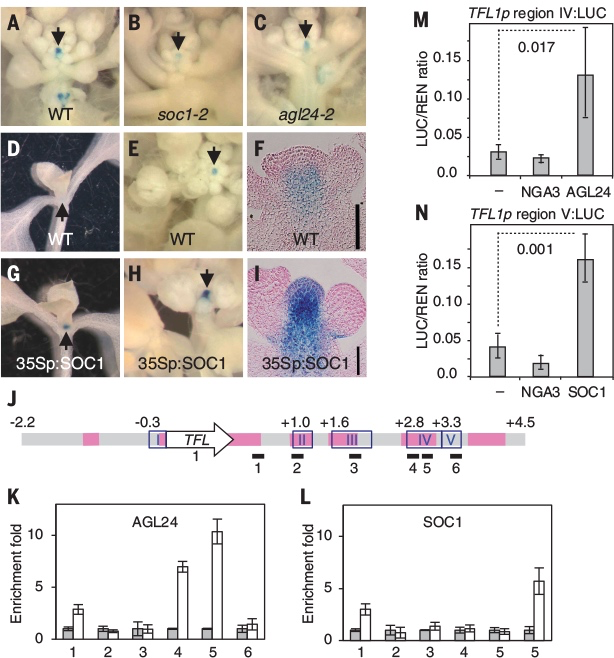
此外因為二者的同系物 XAL2 也結合並誘導 TFL1[23],論文將 SOC1、AGL24 和 XAL2 的活動聚合到 SAX 代理中,一起充當 TFL1 正向調節器[9]。由此創建了 SALT基因調控網絡(圖7),由這四個調節器、生長素Auxin [24]和代表成花激素的F值組成。後者是一種誘導花的信號,當植物老化或暴露於誘導開花的環境條件時該信號會增加[25, 26]。最後研究還在網絡中添加了一個TFL1 的早期過渡抑制因子代理(eREP)。

SALT網絡的真實基因表達概括了在分子層次會驅動植物分生組織成為何種命運。然而,最終植物結構不僅取決於分生組織的類型,還取決於形態動力學參數,包括決定通路的分子閾值、器官生長速率、分生組織開始生成器官的延遲以及器官生產速率,這些都是獨立調節的。LFY 和 ap1 cal 突變體實例説明了這一點,它們具有相同的GRN輸出(圖8C),但具有明顯不同的結構和形態[8, 29]。
因此,最終植物花序結構源於花基因調控網絡 (GRN) 和形態動力學參數之間複雜的相互作用。為研究這種相互作用在擬南芥中是如何運作的,還需要結合動力學進行 3D植物計算建模。
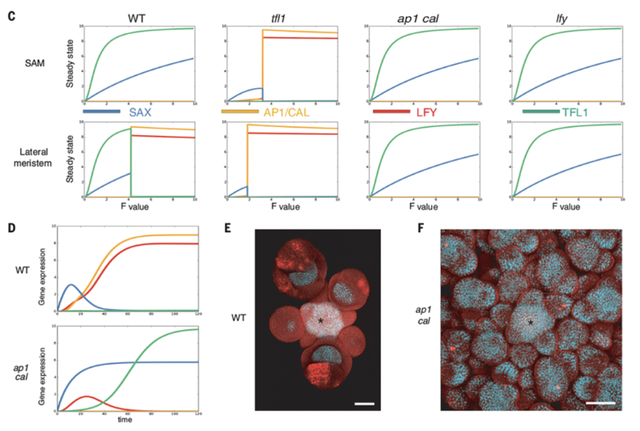
(圖8 SALT GRN模型及實驗驗證 (A)SALT GRN網絡結構 (B)SAX、AP1/CAL、LFY和TFL1在 WT 和 ap1 cal 突變體的分生組織(SAM)和側原基中的已知表達模式。問號表示模型的預測表達模式。(C)在SAM(低生長素)和側分生組織(高生長素)中不同F值下模型的 WT、tfl1、ap1 cal 和 lfy 穩態。預測的 WT 和所有突變體分生組織的遺傳特性與實驗觀察到的表型一致 (D)高F值下側原基基因表達的時間模擬 (E&F)SOC1:GFP(白色/淺藍色信號)基因報告在WT(E)和 ap1-7 cal-1 突變體(F)中的花序表達)
3 形態動力學和GRN結合的多尺度生成模型
基於SALT GRN,作者將L系統(L-System)集成一個到3D計算圖形模型:由塑造地面植物結構的四種器官構成:分生組織(meristems)、節間(internodes)、花朵和葉子(圖9)。每個分生組織的狀態標識(植株、花序和花朵)由 GRN 穩態 State(t) 決定,每個時間步的計算為分生組織先前狀態和外部因素(植物生長素auxin 和 F)的函數。GRN模型實現為單室常微分方程 (見論文補充材料)。
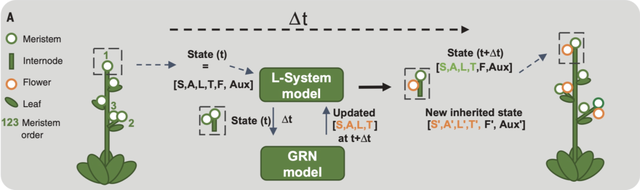
該模型還包含描述器官生長動態的規則(節間和葉片伸長、花的生長、器官產生速度和生長初始延遲)。模擬植物從一個單一植株分生組織開始,根據GRN、形態動力學規則和F的輸入值,不斷重複產生新的器官。通過在合理範圍內的值調整GRN和形態動力學參數,作者成功地校準了模型,產生了 WT 和 lfy 植株及 tfl1 突變體(圖13B-D,movie S1&S2)的真實結構和 SAX 不開花突變體表型。
但模型並沒有模擬出真實的 ap1 cal 突變體,即在沒有苞片或莖生葉的情況下生長出的高階分生組織(圖10a&b),這表明花椰菜表型還涉及額外的調節。

作者推斷,側生的 ap1 cal 花序與其它基因型產生不同,是因為它們只在存於 LFY 的短暫表達中(圖8D)。幾項證據表明,LFY 的短暫表達,會抑制苞片生長[8],也可能有助於高階分生組織釋放。隨後作者通過在模型中引入一個當 LFY 超過最小閾值水平時,會上調的因子X ,抽象出了這個抑制苞片生長並釋放高階分生組織的分子路徑,從而解釋了側生分生組織的遞歸生長。即分生組織會因花信號短暫且不可逆地通路而產生的 ap1 cal 花球結構,且不會改變 WT 原有生長動態(圖13E&H,movie S3)。
因此擬南芥 ap1 cal 和 lfy 具有不同結構(圖8C),是因為它們花序的分生組織分子表達歷史不同,從而揭示了發育滯後的存在。
4 羅馬花椰菜花球的動態發展模型
那麼這個概念框架能否解釋在馴化過程中出現的可食用花椰菜 (Bob) 和羅馬花椰菜變體麼?
作者分析了 Bob 花球的RNA測序數據,確認了先前發現的 BobCAL 基因突變[6, 7, 9],及兩個 AP1 旁系同源基因表達水平遠低於捲心菜的花序。通過比較花椰菜和捲心菜序列,確定 BoAP1 候選調節器結合位點的差異,是它們延遲激活的原因(圖11)。
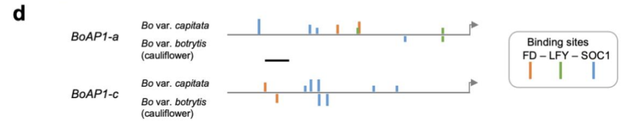
即 BoCAL 失活和 BobAP1-a/c 表達延遲(由順式或反式突變引起的異時性)的組合參與了Bob花球的發展。
與擬南芥 ap1 cal 類似,花椰菜的最大分生組織(n≥7)比捲心菜(n=3到4)的分生組織階數更高(圖12)。儘管如此,單體大塊花椰菜花球的發育卻並不完全等同於擬南芥突變體[5, 7],它還涉及形態動力學參數額外很多因素改變,例如節間伸長的減少和分支直徑的增加影響。

出現在羅馬花椰菜螺旋所有尺度的中的圓錐形狀(圖1F),代表了通過馴化獲得的額外幾何變化,作者發現有幾個形態動力學參數花椰菜發育過程中保持不變,在羅馬花椰菜中卻有所不同:
1. 葉間期,兩個連續分生組織(如葉原基)產生的時間間隔
2. 源自特定分生組織的可視螺旋數
3. 側生起始延遲。以葉間期數衡量,一個側原基開始產生它自己的原基(或延遲側生物)前所需的時間
4. 分生組織的大小
葉序研究[37, 38]表明前三個參數與分生組織大小有關:分生組織中心區域大小的增加會相應減少葉間期,而這又反過來增加了螺旋數和側生起始延遲。
因此論文假設,在分生組織中從恆定到遞減的葉間期,或許可以將花椰菜變成羅馬花椰菜形態。
兩個分生組織平衡被擾動的證據也支持這一假設:羅馬花椰菜偶爾表現出束狀(圖13N-O)、CLV3 的表達低於花椰菜。
作者先使用了一個簡化的純幾何生長模型進行測試,結果表明遞減的葉間期足以產生羅馬花椰菜形狀(圖13G),而該參數的恆定值則產生花椰菜形態(圖13F)。然後在更復雜的基於GRN的擬南芥花椰菜結構模型,通過L系統中引入了相同的變化,同時保持器官生長動態在 WT 上校準。結果雖然不像純幾何模型那樣規整,但花球變成了具有典型圓錐形的羅馬式形態(13H-I)。花椰菜生長公示:
s .PCD (t + Δt) = s.PCD(t) - cte
對羅馬花椰菜而言,隨着分生組織年齡增長,葉間期會更快遞減:
s .PCD( t+ Δt) = s.PCD (t) - (cte)(s.AGE )
(公式:以L系統實現遞減的葉間期,L系統是生成分形的一種方法)
在模擬之後進行實驗驗證。通過在 CLV3 基因中引入突變,直接改變分生組織的大小,對擬南芥進行實驗測試這一假設。CLV3基因控制分生組織穩態並在生長過程中誘導分生組織中心區增加[29, 30]。結果如預測所料,ap1 cal擬南芥突變體中引入 CLV3 突變後,失去了球形並獲得了更錐形的形狀,且在不同的尺度上具有相似的結構,即羅馬式花球標誌特徵[31](圖13L&M)。即實驗觀察結果也表明,分生組織大小通過控制葉間期值來調節羅馬花椰菜最終花球形態。

總結而言,論文建立了影響植物分生組織表達的SALT基因調控網絡,並結合形態動力學建立一套植物器官形態發育的多尺度生成模型。其結果揭示瞭如何通過改變身份標識,影響植物動態生長和發育網絡,使分生組織獲得了不同的特性,並輔助調節形態發生學種種參數,最終使得自然界產生的高度多樣化的植物器官和迷人的結構如分形等特徵。
5 生物數學中班圖動力學:動態發生學與基因調控網絡
在以往研究中,生物學家只能對生物形態發育問題博物學式地總結出規律,在環境或基因網絡找到幾個影響表觀或調控發育的因素,或者如達西・湯普森,他在1917年的著作《生長與形式》中提出的,動物身體的形狀是由不同方向和大小的生長速度造成的。然而這也只是涉及描述層面而非機制層面探討問題。
只有計算理論和人工智能的奠基人之一圖靈,在1952發表的的《形態發生的化學基礎》[27]中,建立了一個形態發育及斑圖生成問題的形態發生學框架,在這個框架中,圖靈把斑圖生成的化學基礎歸結為初始發育系統的對稱性破缺:其中作為化學物質的形態發生體,會在激活劑(Activator)和抑制劑(Inhibitor)兩種形式作用下不斷擴散,如果擴散抑制劑要比激活劑速度更快,就會在不同條件下就會產生不同種類形態各異的斑圖。

從80年代末至90 年代初,我國歐陽頎院士及其合作者在非線性動力學實驗研究中首次發現二維穩態Turing 斑圖,證實了Turing 理論的正確性,並有力地推動了Turing 斑圖動力學的發展。在2014年,在 PNAS上發表的一篇由 Brandeis大學和 Pittsburgh大學的研究人員完成的論文《Testing Turing’s theory of morphogenesis in chemical cells》[28],通過類細胞結構,也首次為圖靈的理論提供了完整實驗證據,驗證了他提出的模型。2018年和2020年,浙江大學張林教授和復旦大學徐凡教授又分別把圖靈結構應用到了納米尺度的化學膜結構和液體對植物葉片的生長上。此外應用圖靈結構對種族入侵、擴散和捕食者系統的研究也在深入展開中[32]。
儘管曾經有諸多質疑,很多生物學家認為圖靈框架不能解釋這麼複雜的生物系統。但從近些年的種種研究來看,尤其在彌補了尋找基因調控網絡的缺失後,越來越多的證據表明Turing 系統提供了描述生物系統斑圖形成的總體理論框架,能夠揭示從自然系統到生物系統、以及種族空間擴散的生態系統等各類系統的斑圖動力演化情況。
即使在基因網絡研究中,例如本次對花椰菜的研究,我們也發現其實基因網絡的調控也是由激活因子和抑制因子構成的,它們一起調控了植物生物發育的初始參數;因此可以説圖靈斑圖模型是一個跨越所有層級系統的動力學框架,如今生物學家和數學家、計算機科學家聯手,再結合分子遺傳學和形態發生學,才終於能對這個橫跨數學、生物學、遺傳學、複雜動力學系統的現象做出一個完整解釋了。
這是生物學家的勝利,更是偉大圖靈的勝利。它不僅證明了自然、植物和各種動物懂數學,而且更説明了:唯有我們懂數學、研究數學,才能理解懂數學的生命和世間萬事萬物。
參考文獻
[1] The Mathematics of Life,Ian Stewart,2011
[2] Helmut Vogel,1979
[3] C. Godin, C. Golé, S. Douady, Development 147, dev165878 (2020).
[2] C. F. Quiros, M. W. Farnham, “The genetics of Brassica oleracea,” in Genetics and Genomics of the Brassicaceae, R. Schmidt, I. Bancroft, Eds. (Springer, 2011), pp. 261–289.
[3] D. V. Duclos, T. Björkman, J. Exp. Bot. 59, 421–433 (2008).
[4] L. B. Smith, G. J. King, Mol. Breed. 6, 603–613 (2000).
[5] N. Guo et al., BMC Biol. 19, 93 (2021).
[6] J. L. Bowman, J. Alvarez, D. Weigel, E. M. Meyerowitz, D. R. Smyth, Development 119, 721–743 (1993).
[7] S. A. Kempin, B. Savidge, M. F. Yanofsky, Science 267, 522–525 (1995).
[8] G. Denay, H. Chahtane, G. Tichtinsky, F. Parcy, Curr. Opin. Plant Biol. 35, 15–22 (2017).
[9] A. Pajoro et al., J. Exp. Bot. 65, 4731–4745 (2014).
[10] B. Thomson, F. Wellmer, Curr. Top. Dev. Biol. 131, 185–210 (2019).
[11] K. E. Jaeger, N. Pullen, S. Lamzin, R. J. Morris, P. A. Wigge, Plant Cell 25, 820–833 (2013).
[12] C. Espinosa-Soto, P. Padilla-Longoria, E. R. Alvarez-Buylla, Plant Cell 16, 2923–2939 (2004).
[13] F. Leal Valentim et al., PLOS ONE 10, e0116973 (2015).
[14] P. Prusinkiewicz, Y. Erasmus, B. Lane, L. D. Harder, E. Coen, Science 316, 1452–1456 (2007).
[15] K. Goslin et al., Plant Physiol. 174, 1097–1109 (2017).
[16] C. Ferrándiz, Q. Gu, R. Martienssen, M. F. Yanofsky, Development 127, 725–734 (2000).
[17] D. Bradley, O. Ratcliffe, C. Vincent, R. Carpenter, E. Coen, Science 275, 80–83 (1997).
[18] X. Hou et al., Nat. Commun. 5, 4601 (2014).
[19] S. K. Yoo et al., Plant Physiol. 139, 770–778 (2005).
[20] A. Serrano-Mislata et al., Development 143, 3315–3327 (2016).
[21] R. V. Pérez-Ruiz et al., Mol. Plant 8, 796–813 (2015).
[22] D. Reinhardt et al., Nature 426, 255–260 (2003).
[23] P. A. Wigge, Curr. Biol. 21, R374–R378 (2011).
[24] J. Putterill, E. Varkonyi-Gasic, Curr. Opin. Plant Biol. 33, 77–82 (2016).
[25] C. Liu et al., Dev. Cell 24, 612–622 (2013).
[26] O. J. Ratcliffe et al., Development 125, 1609–1615 (1998).
[27] https://royalsocietypublishing.org/doi/pdf/10.1098/rstb.1952.0012
[28] https://doi.org/10.1073/pnas.1322005111
[29] J. C. Fletcher, U. Brand, M. P. Running, R. Simon, E. M. Meyerowitz, Science 283, 1911–1914 (1999).
[30] M. Kitagawa, D. Jackson, Annu. Rev. Plant Biol. 70, 269–291 (2019).
[31] L. E. Watts, Euphytica 15, 224–228 (1966).
[32] 生物數學模型斑圖動力學。王瑋明,蔡永麗,2020.12
本文經授權轉載自微信公眾號“集智俱樂部”。