1+1=1…吧？_風聞

原創：中科院物理所

　　你憑什麼認為 1+1=2 ？

　　如果我説 1+1=1 ，我們可以構造出怎樣的數學？

　　讓我們首先考慮一個可以説是最基本的數學公式：

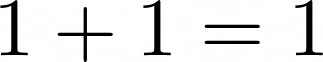
　　這可能是我們小時候學到的第一個等式。我們中有些人可能對此還有模糊的記憶：我們的父母把它重複了一遍又一遍，直到我們設法掰着手指去理解它。

　　等等，你可能會提出反對意見。這個等式有點小問題啊！不應該是：

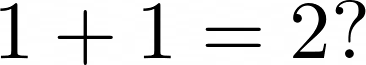
　　那麼我要問你，你怎麼知道“應該是這樣的”？

　　你可能會説，這不是很明顯嗎？當你把一個彈珠和另一個彈珠放在一起，你會得到兩個彈珠！你小時候你父母沒給你演示過嗎？

　　1 + 1 = 1?

　　根據經驗主義者的觀點，**我們通過經驗獲得數學知識。**這可以從我們如何通過與周圍世界的互動來學習數學中看出。例如，我們的父母可能教我們用周圍的各種物體數數或做一些簡單的算術。

　　但正如開頭的的這個思想實驗所表明的那樣，這種數學觀似乎存在一個問題——我們從世界上獲得的知識是不確定的。為了理解為什麼會這樣，我們必須更仔細地研究我們是如何學習 1+1=2 的。

　　假設一個孩子要開始學習 1+1=2 。首先，父母可能每隻手拿一個彈珠，然後再把它們放在一起，讓孩子看到現在有兩個彈珠。他們也可能用餅乾、鉛筆、數學課本之類的來重複這些演示。

　　一段時間後，孩子將開始意識到這個模式，並得出 1+1=2 的（正確的？）結論。通過這種方式我們看到，孩子從一個有限數量的樣本開始，將一個對象和另一個對象相加，然後再總結他的經驗來得出等式。

　　問題是，這種總結方法——也被稱為歸納法，它也有可能會帶來一些錯誤。如果我們遵循這樣的邏輯，有時會遇到例外情況，比如説我們將一杯水和另一杯水相加將導致我們得出一個非常不同的結論。

　　因此，雖然我們可以通過經驗來學習數學，但經驗並不能作為數學的全部依據。換句話説，雖然我們可以通過操控各種對象來了解 “1+1=2” 的含義，但這並不是該命題為真的原因。這一點至關重要，特別是當我們想確認數學知識的正確性的時候。

　　經驗主義不是數學知識的最佳來源的另一個原因是，它無法解釋我們如何獲得關於理想和抽象實體的知識，而這些實體在現實世界中並不存在。例如，一條線被定義為有長度但沒有寬度的對象，但是現實世界中我們不可能繪製出或感知到一條線。無論你畫的多好，即使它是由計算機繪製的，它在數學上也不是完美的線，因為在放大後，“線”只是一系列相鄰的像素，它們具有寬度。如果這些數學對象在現實世界中不存在，我們怎麼能僅僅通過我們的經驗來想象它們呢？

　　出於上述原因，數學通常被視為一門先驗學科，這意味着我們需要通過理性而不只是經驗來認識它。這是因為像 1+1=2 這樣的命題被視為是分析性的，也就是説，根據定義是真的。這意味着否命題 “1+1≠ 2” 是假的，這一點僅僅通過思考（也就是説僅使用理性）就可以明顯看出。其他例子包括 “三角形有三條邊” 或 “平行線永不相交” 。這樣一來我們現有的數學知識就是確定的了，因為如果你説 “1+1=1” 或 “三角形有四條邊” ，這些命題首先在邏輯上就是不正確的。

　　Not a triangle.

　　非三角形

　　但這仍然不能解釋我們是如何得出這樣的結論的。要回答這個問題，我們必須轉向最一般的數學觀點：柏拉圖主義。

　　在柏拉圖主義中，數學實體是抽象的、永恆的、永不改變的。它們存在於形式世界中，獨立於物理世界。當我們做數學的時候，我們用我們的頭腦進入這個形式的世界，發現其中的真理。例如，我們知道三角形有三條邊，因為這就是完美三角形在這個“形式世界”中的存在方式，我們可以通過使用我們的理性來了解它。

　　你可能認為形式世界的概念有點奇怪，但請允許我換個説法。因為像完美的圓和線這樣的數學實體在現實世界中並不存在，它們必須存在於某個地方。否則我們怎麼知道他們？它們存在的地方正是柏拉圖主義者所説的形式世界！

　　Perfect shapes enjoying life in the World of Forms

　　形式世界的完美圖形

　　這也符合數學的先驗性質，因為數學的正確性不在於實體或定理能否在物理世界中找到，而在於我們能否在形式世界中找到它。例如，我們沒有通過測量多個物理三角形來證明三角形中內角之和為 180° 。取而代之的是，我們使用了一個我們可以在精神上發現的證據，讓我們能夠接近這樣一個真理：三角形的內角之和等於 180° 。

　　此外，它還解釋了為什麼數學是普遍正確的。當我們聚在一起時，我們都會同意 1+1=2 或者畢達哥拉斯定理是正確的，因為數學是獨立於我們的思想而存在的。這意味着我們都可以訪問存在於形式世界中的同一套通用數學規則和實體。事實上，像萊布尼茨和牛頓這樣的人獨立於他人發明微積分，這也證明了這一點。

　　然而，正如許多人會指出的那樣，“形式世界”的模糊概念並不能真正準確地解釋數學實體存在的位置和方式，以及我們是如何瞭解它們的。這似乎有點奇怪，好像有一個神秘的領域，像完美的線條和圓圈這樣的物體只是在那裏存在，等待着我們以某種方式偶然發現它們。這就是為什麼有些人可能更喜歡以下觀點：直覺主義。

　　根據直覺主義者的説法，我們在一些抽象的領域中並沒有發現數學實體。更確切地説，數學是由人類的思維構建的。

　　所有人對數學都有一種原始的直覺，從自然數 1、2、3 開始……這意味着我們對數字1的含義有一個直接理解，並且形成數字 1 的心理過程可以重複得到 2，然後是3，依此類推。接下來，我們可以構建數學的其他領域，如算術、代數和集合論。

　　這種觀點很有吸引力，因為它仍然堅持數學是先驗的和普遍的。由於數學命題的構造是一種心理活動，它是一種先驗行為，這使我們能夠確定像 1+1=2 這樣的命題是正確的。此外，所有人對數學都有相同的直覺，這一事實允許我們提出相同的數學並達成一致。

　　此外，根據德哈恩(D­ehaene）的説法，數學是被構造出來的的這一論點似乎提供了“數學與人腦之間關係的最佳解釋”。現代心理學似乎支持原始數學直覺的觀點，它認為我們有某些固有範疇，而我們根據這些固有範疇來理解世界。例如研究發現，嬰兒天生就具有區分對象和提取小集合數量的先天能力，而在幼兒中，簡單的算術似乎在沒有太多明確指示的情況下自發出現。因此，直覺主義似乎是我們如何做數學的最好解釋。

　　然而，直覺主義也有一些缺點。它的主要問題是，雖然許多定理可以用古典和直覺兩種方法來證明，但直覺性定理通常要長得多，因而看起來不那麼優雅，這導致許多數學家不願接受它們。

　　儘管如此，我們知道優雅與否並不是檢驗真理的標準，因此僅僅因為直覺主義不如柏拉圖主義優雅而拒絕直覺主義並不是最合理的做法。

　　總而言之，一個簡單的思維實驗説明了為什麼看似直觀的數學觀經驗主義是站不住腳的，然後我們比較了兩種關於我們如何獲得數學知識的觀點：柏拉圖主義和直覺主義。由於數學家和哲學家在這個問題上仍然存在分歧，我選擇讓讀者來決定你們更喜歡哪一個。但同時，我希望這篇文章能讓你更深入地理解我們所説的 1+1=2 的真正含義。

　　作者：Xavier Lien

　　翻譯：Nothing

　　審校：Dannis

　　原文鏈接：

　　https://www.cantorsparadise.com/what-makes-you-so-sure-that-1-1-2-659001f741ba