蒙特卡洛方法計算圓周率_風聞

文/陳新龍

圓周率（Pi）是圓的周長與直徑的比值，一般用希臘字母π表示，是一個數學中最基本的常數之一。π也等於圓形之面積與半徑平方之比，是精確計算圓周長、圓面積、球體積等幾何形狀的關鍵值。它是一個無理數，即無限不循環小數。在日常生活中，通常都用3.14代表圓周率去進行近似計算。這裏我想問大家幾個問題：圓周率是誰發明的？從前的人們是怎麼樣推導出圓周率的呢？今天我們在Python中用一種概率算法“蒙特卡洛方法”來計算圓周率吧。

蒙特卡洛是一座位於歐洲摩納哥公國的賭城，這個地名也象徵概率。蒙特卡洛方法是由大名鼎鼎的數學家馮·諾伊曼在上世紀40年代參與美國研究原子彈的“曼哈頓計劃”時提出的。這個方法的原理是通過大量隨機樣本，去了解一個系統，進而得到所要計算的值。

蒙特卡洛方法在計算圓周率時設一個正方形內部相切一個圓，這時圓和正方形的面積之比是π/4。在這個正方形內部，隨機產生n個點（這些點服從均勻分佈），計算它們與中心點的距離是否大於圓的半徑，以此判斷是否落在圓的內部。統計圓內的點數，與n的比值乘以4，就是π的值。理論上，n越大，計算的π值越精確。

首先引入random庫和time庫，調用random和perf_counter，再編寫一個計時函數start用來計算得出圓周率所需要的時間，然後通過循環編寫模擬撒點代碼，讓計算機每次隨機生成兩個0到1之間的數（設圓的半徑為1），看以這兩個實數為橫縱座標的點是否在單位圓內，因此我們實際只是計算了1/4圓，但不影響結果。通過生成一系列隨機點，統計單位圓內的點數與總點數，當隨機點獲取越多時，其結果越接近於圓周率。計算出結果後將圓周率和計算的時間輸出結果。

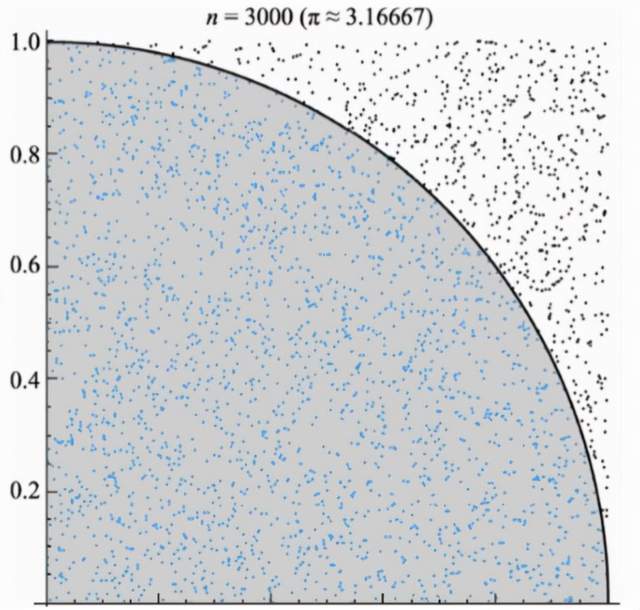
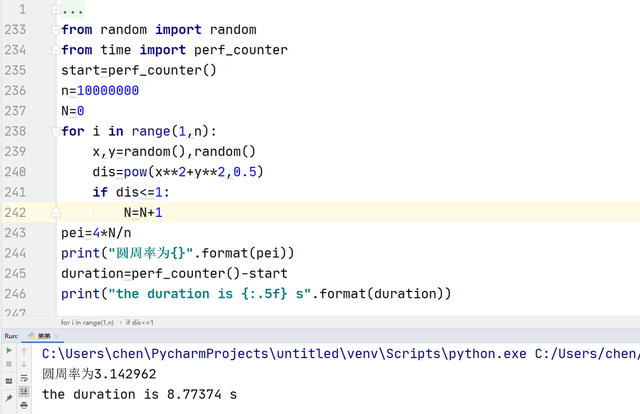
通過比較點到圓心的距離判斷點是否在圓內，利用計算機的運算速度，可以很快統計出多次撒點的結果，即使我們計算1000萬次，也只需要8.7秒（具體計算時間與計算機運行速度相關）。根據運算結果來看即使有這麼大的數據量使用概率算法求出的π精度依然不夠高。