同樣是關於質數,為啥哥德巴赫猜想比我有名?_風聞
中科院物理所-中科院物理所官方账号-2021-09-14 14:14
原創:中科院物理所
質數是那些只能被自身和1整除的整數,比如前七個質數是2,3,5,7,11,13,17。
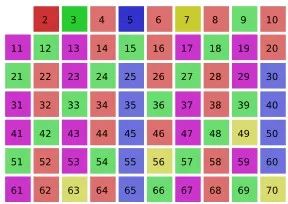
圖示為埃拉托色尼篩選法,可以用於尋找質數。
圖源 SKopp, CC BY-SA 3.0.
每一個正整數都可以藉助一種特定的數學結構寫成質數的乘積,例如 30 = 2×3×5 。質數就像是構成其他整數的基本積木,而這就是人們覺得它們有趣的原因。
質數是無窮多的,而這一點早已被古希臘數學家熟知,無論你在數軸上移動多遠總有一個質數在你前面。下面是希臘最著名的數學家歐幾里得的證明。
假設質數是有限的。我們可以用 p1 , p2 , p3 等來表示,直到最後一個質數 pn 。現在定義某個數字 P :
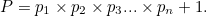
比方説如果只有5個質數:p1 = 2, p2 = 3, p3 = 5, p4 = 7, p5 = 11,那麼存在一個數 P :
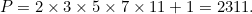
如果 P 本身是質數(就像在我們的例子中一樣),那麼很明顯它不可能是我們列表中的一個質數:因為它比所有的質數都大。如果 P 不是質數,那麼,就像其他自然數一樣,它一定可以寫成質數的乘積。我們選一個能被 P 整除的質數,用 p 表示。可以看出, p 不能是 p1 到 pn 的任何質數,否則就會出現餘數 1 :
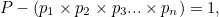
而 1 不能被任何其他的自然數整除。因此,集合 p1,p2,p3…pn 並不能包含我們假設的所有質數。這個矛盾意味着質數一定是無限多的。
幾千年來,我們一直知道有無限多個質數(參見這裏的證明),但並沒有一個簡單的公式告訴我們它們都是多少。強大的計算機算法使我們能夠找到越來越大的質數,但卻永遠不可能把它們全部寫下來。
質數定理告訴我們質數在其他整數中的分佈。它試圖回答這樣一個問題:“給定一個正整數 n ,包括 n 在內的所有整數,有多少個是質數?”
質數定理並沒有精確地回答這個問題,而是給出了一個近似值。寬泛地説,對於比較大的整數,表達式:
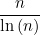
是一個很準確的質數估計,而且隨着n的增大,這個估計也會變得更準確。其中 ln(n) 是自然對數,可以通過計算器得到。
舉個例子,讓我們來看看 n=1000 的情況。此時所有質數可以在這個列表中查找。我們的估計是:
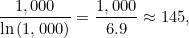
這是一個很準確的近似。
然而,要精確地理解質數定理告訴我們的東西,我們需要説出我們所説的“一個準確的近似”是什麼意思。質數定理並不是説,對於一個給定的整數n,真值和我們的近似值之間的差值接近 0 。相反,它告訴我們關於“近似值佔真值的百分比是多少?”的問題。
回到我們 n=1000 的例子,真值是 168,近似值是 145 。因此,近似構成的比例:
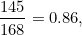
近似值佔真實值的 86% ,不錯。
當 n=100000 時,包含 100000 的質數是 9592 ,這是真值,估值是 8686 。
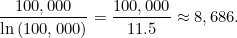
在這種情況下,估值佔真值的 90% 。
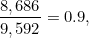
這相比於 n=1000 的情況,比例從 86% 提升到了 90% 。
一般來説,質數定理告訴我們,對於 n 很大的情況, n/ln(n) 得到的近似值幾乎是真值的 100% 。事實上,你可以讓它接近 100% ——只要你選擇足夠大的 n 。
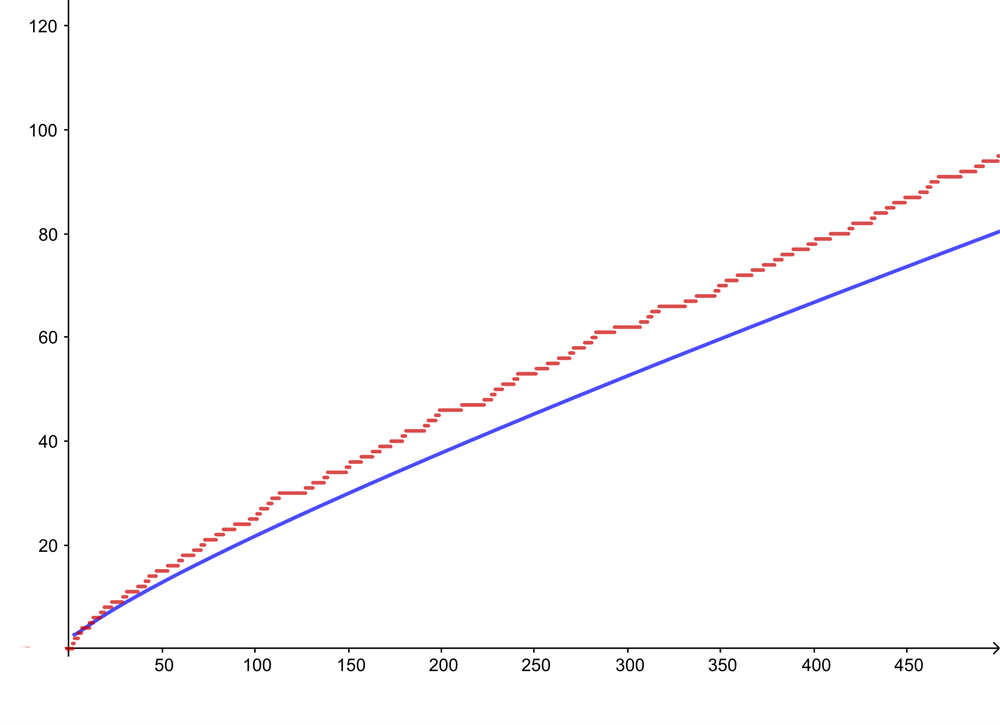
紅色曲線顯示的是小於或等於n的質數數目,其中橫軸表示 n 。藍色曲線給出 n/ln(n) 的值。真實結果和近似結果之間的差值隨着 n 的增長而增加,但兩者之間的比值趨於 1 。
為了用數學符號來描述素數定理在數學上的輝煌,讓我們先用表示小於或等於的質數的數目。這個定理可以用公式表述:
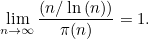
(1)
如果你懂一點微積分你就會知道你可以交換分子和分母,此時表達式 (1) 等於:
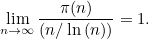
(2)
素數定理通常用第二個表達式 (2) 來表述,有時也寫成:
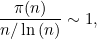
表示:“當 n 趨近於無窮大時, n/log(n) 趨近於 π(n) ”。
作者:Marianne
翻譯:C&C
審校:zhenni
原文鏈接:
https://plus.maths.org/content/maths-minute-prime-number-theorem
https://plus.maths.org/content/maths-minute-how-many-primes