座標系是如何誕生的？_風聞

撰文 | 張偉偉

我們知道，座標的意義在於將代數與幾何聯繫起來，使兩者貫通，使得能對自然進行數學描述。在力學分析中，可能不會有人懷疑座標的價值，可以説力學的每一個分支都依賴於一定的座標系。力學所研究的物體，每個都有自己的位置和形狀，形狀描述需要座標；所研究的範疇，無論運動還是變形，還是需要座標；有了座標，力學描述才變得簡潔、明瞭，很難想象，如果沒有了座標，力學會如何演繹。然而，座標系雖然看似簡單、但它形成卻是一個十分漫長的過程。

從本質上講，座標就是一種位置參考。古代的天文學家們為了確定出天空中星星的位置，自然的用到了某種類似於座標的方法，即對天空進行網格劃分，根據網格位置來確定星體位置。古希臘天文學家喜帕恰斯（Hipparchus，約前190-前125，另譯為依巴古，這是由於希臘文、拉丁文、中文翻譯過程中所造成的）運用經度和緯度標出天空中點的位置，這就像是給天空畫上了網格，利用網格可以標記和快速的找到各類星星。

歐多克索斯（Eudoxus of Cnidus, c.408-c.355BC）是古希臘早於喜帕恰斯的天文學家和數學家，曾向阿契塔和柏拉圖學習過，他也曾使用過一種座標體系標記天空中的星體位置。喜帕恰斯曾評價歐多克索斯在描述恆星位置時採用了恆星的極距（相當於赤道系統的偏角）、赤經（赤道，以赤道為參考面）、經度（黃道，以黃道面為參考）、極經度（混合兩種參考），但沒有提供天體緯度。

如果在平面上，經度相當於水平線，緯線相當於豎直線，從喜帕恰斯對歐多克索斯的評價可以看出，歐多克索斯的座標系統，只能確定出星星的高度，並不能準確的定位星星。喜帕恰斯引入緯線，則可以準確的定位星星。

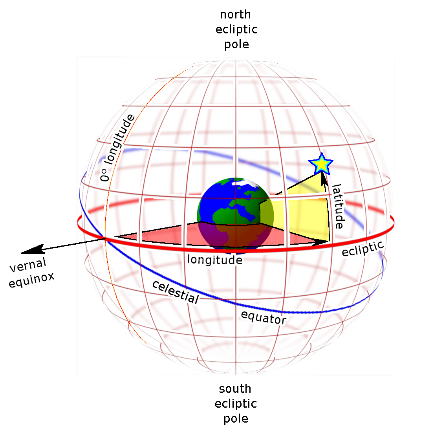(a)黃道座標系

地球繞太陽公轉的軌道平面稱為黃道，以黃道為參考平面

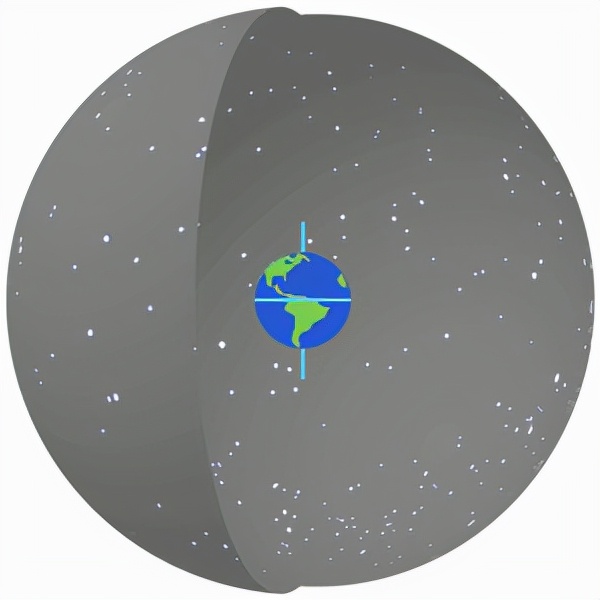(b)赤道座標系

假想過天球中心與地球赤道面重合的平面為赤道面，以赤道面為參考平面

圖1 兩種星空座標系

後來這種網格座標被古希臘數學家進行了改進，他們在一個平面底部畫出一條水平線，然後在左側畫出一條垂直線（有時是傾斜的），平面內任意點的位置通過該點到水平線和垂直線之間的距離來確定。這樣做的意義主要有兩點：首先，把可見的網格轉變成了隱形的網格，使空間看起更簡潔；其次，由於測量距離的需求，引入了標準的公共設備——尺子，這就向着標準座標系邁出了重要一步。

現在已無法考證是誰首先使用了這種方法，但是之後的阿波羅尼奧斯（Apollonius of Perga, c.262– c.190BC）在座標系上的貢獻被給予了極高的評價，阿波羅尼奧斯的座標體系直接將古希臘幾何一口氣帶到費馬、笛卡爾等人發明現代座標系之前（Wiki百科中的描述），阿波羅尼奧斯本人也被稱為是古希臘僅次於阿基米德聰明的人。我們今天使用的橢圓、拋物線和雙曲線的定義就是由他提供的，他還利用偏心軌道解釋了行星為什麼會有異常運動，這或許為開普勒偏心的行星運動軌道提供了啓示。

在阿波羅尼奧斯的座標體系中，他將水平線稱為“直徑”，這個稱謂大概是因為古希臘對直徑一詞的含義要廣一些，在圓錐圖形中（如拋物線、橢圓、圓），將過頂點平分圖形的直線。他將點到該“直徑”的直線距離稱為tetagmenos（意為“擴展”），類似於我們現在的縱座標，這種情況下，“直徑”就是我們熟知的x軸，“頂點”就是座標原點，他將y軸定義為曲線的切線（參見圖2）。

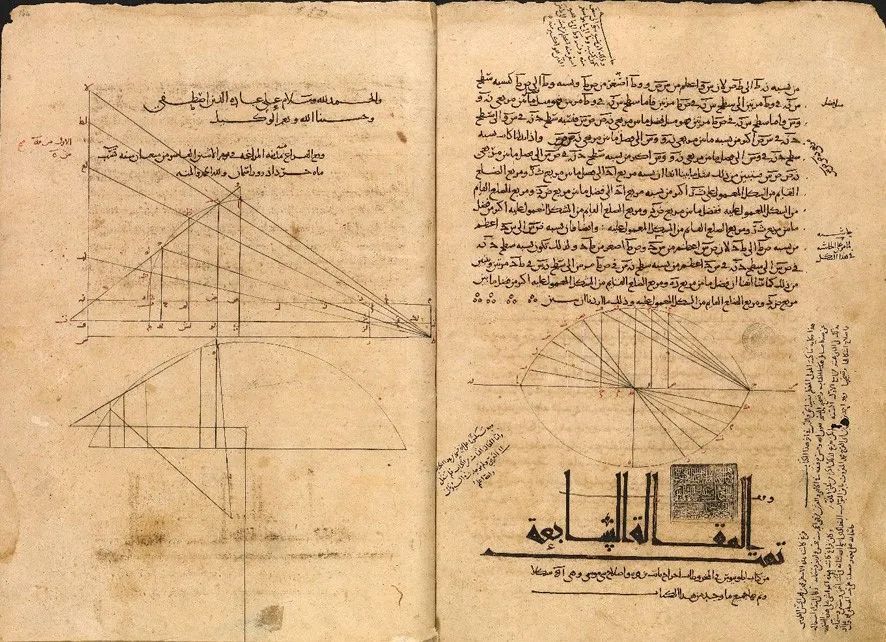圖2 阿波羅尼奧斯《偉大的幾何》中的插圖

The Conica of Apollonius ofPerga ‘the great geometer’ (c. 262-190 BCE) were translated into Arabic in the9th century CE

這樣，我們已經看到阿波羅尼奧斯已經區分出了x軸，y軸，座標原點，儘管它們使用了不同的稱謂。在外在形式上，他的座標軸只是一條直線，並沒有方向，也沒有負軸，相當於今天只在笛卡爾座標系第一象限中進行研究。現代座標系的建立並溝通代數與幾何之間的聯繫，主要是費馬（Pierre de Fermat, 1607-1665）和笛卡爾（RenéDescartes, 1596-1650）的貢獻。

費馬關於座標系的工作是從阿波羅尼奧斯的《論平面軌跡》開始的，他借用了韋達（François Viète, 1540-1603）在代數中系統地使用字母表達的方式，這為代數方法在幾何中應用提供了便利條件。如圖3所示，設有任意曲線，其上的點標記為J，J的位置由A、E給出（圖中它們分別表示OZ和ZJ線段的長度），這個座標系相當於現在的傾斜座標系。費馬的座標系被認為是利用韋達的現代表示方法，重新翻譯了阿波羅尼奧斯的座標系。特點是沒有使用y軸，沒有負座標軸。

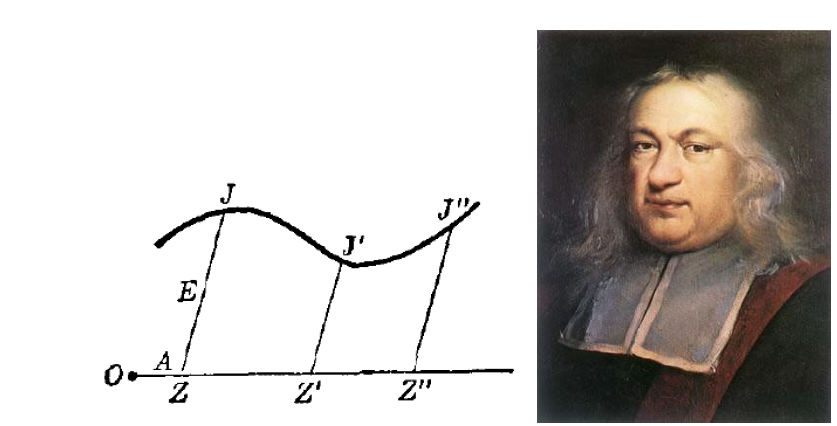圖3 費馬和他用座標圖形表達的曲線方程

費馬敍述出了一條基本原則：只要在最後的方程裏出現兩個未知量，我們就得到一個軌跡，這兩個量之一，其末端就描繪出一條直線或曲線，即J點的描繪出的軌跡。例如圖3中，用x、y表示A、E，它們之間的關係就表示該曲線的方程，它的意義在於利用座標系表示了代數方程，給出了曲線方程的意義，這無論是對於幾何還是代數都是巨大的進步。

笛卡爾在座標系上的工作更進一步，他首先批評了希臘幾何與代數的不足，他稱歐幾里得幾何中每一個證明，總是依賴於某種新奇的技巧，缺少可以通用的一般方法，這使得人們在想象力大大疲乏的情況下去練習理解力（幾何的證明有時讓人摸不着頭腦）。他也批評代數，説它完全受法則和公式的控制，以至於成為一種充滿混雜與晦暗，成為阻礙思想的藝術，而不是一門改進思想的科學（代數太過於抽象，不便於理解）。

但是，幾何與代數的優點也是顯著的，幾何的形象直觀，代數作為一般科學方法的重大優勢，引起了笛卡爾的關注。這便促使他產生了把代數應用到幾何中，發展一種同時融合兩種方法優點的想法。這就是他的《幾何》一書，他也採用韋達的字母體系。笛卡爾座標系就是這一過程中提出來的，他主要完成了以下幾個方面的工作：

1. 利用方程思想解決作圖問題。例如假定某個幾何問題歸結為尋求一個未知長度的線段，設為x，並且知道x滿足關係x^2=ax+b^2，其中a和b為已知長度。由代數給出的結果為

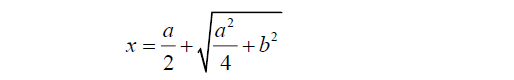笛卡爾只考慮正根，不考慮負根。他強調對於未知量，必須假定已知，然後建立方程。

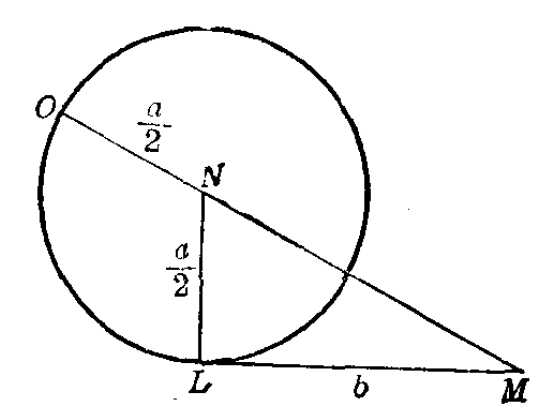圖4 笛卡爾利用代數解決幾何作圖問題的一個例題

2. 座標系中的方程曲線。對於不確定問題，結果可能有許多長度作為答案，將這些長度的端點連接起來將成為一條曲線。笛卡爾的做法是先選定一條直線作為基線，如圖5所示的A點為原點，x是基線上從A點量起的長度AP，y是PC的長度，它與基線所成角為固定角。

可以看出，笛卡爾與費馬繪製曲線的方法，以及座標的使用基本一致。但是我們看到，笛卡爾座標系中原點A的兩側都有點或線，笛卡爾曾附帶的討論過取負座標軸的情況，但是他並沒有提出負軸的概念，他對座標的討論依然以第一象限為主。

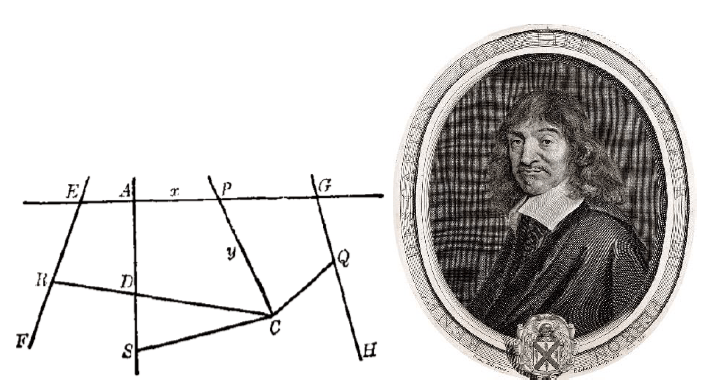圖5 笛卡爾和他使用的座標系

3. 笛卡爾建立了一般方程與曲線的關係，極大擴展曲線的範疇。古希臘只認為可以同直尺和圓規作出來的曲線為可靠曲線，但笛卡爾認為只要給定一個含x和y的代數方程，人們都可以求出它的曲線，這些曲線有些是全新的。因為在古希臘，人們只認可平面曲線（尺規作出的曲線）、圓錐曲線和少數的特殊曲線，如蚌線、螺線、割圓線和蔓葉線等。

4. 笛卡爾藉助於座標從事光學研究，給出了折射定律（這個定律一般認為是Snell給出，笛卡爾是否獨立完成仍有爭論）。笛卡爾還設計了一種能將光線匯聚在一點的透鏡。他還解決了一個一般性問題：什麼樣的曲面作為兩種介質的交界面時，從第一種介質內一點發出的光線射到曲面上折射進入第二種介質恰好匯聚於一點。笛卡爾給出了一種卵形線，並給出了曲線方程。

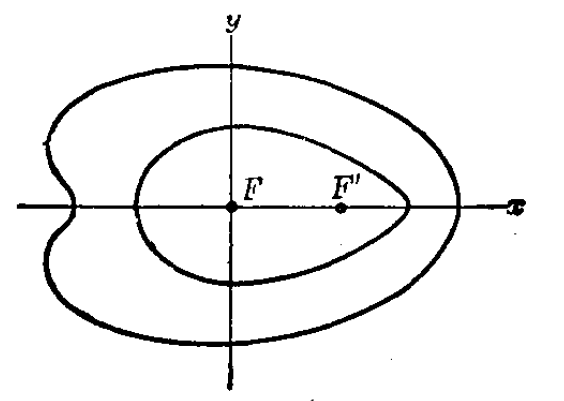圖6 笛卡爾卵形線（座標系是後人加的）

費馬對於座標的研究主要目的在於繼承希臘人的思想，主要是阿波羅尼奧斯的思想。但笛卡爾利用座標提出了更為一般的處理方法，大大超越了費馬。也正是由於笛卡爾，使人們認識到了座標系的偉大，並由此誕生了解析幾何。

但是，笛卡爾有關座標的發明，起初並沒有得到科學家的歡迎。許多科學家認為笛卡爾只是提供了一種幾何分析方法，所得到了科學結論仍沒有挑出古希臘幾何成就，只能説這些科學家只看重知識本身（幾何知識）而沒有發現獲得這些知識方法（座標幾何法）的價值。

另一個原因來自於笛卡爾自身。笛卡爾為了表示自己工作的高深，許多地方故意寫的模糊不清，他曾自稱説歐洲的數學家幾乎沒有一個人能看懂他的著作。在一些地方故意做了刪減，稱他不願意奪去讀者自行加工的樂趣，這或許是一種冠冕堂皇的説法，實際上是擔心如果書寫的太過於易懂，那些自命非凡的人將會稱笛卡爾所寫的東西都是他們已知的東西（歐洲科學界多項優先權之爭的副作用）。

隨着笛卡爾解析幾何的推廣，座標系也逐漸被改進與完善，這主要得益於範斯庫藤（Frans van Schooten,1615-1660）和沃利斯（John Wallis, 1616-1703）。範斯庫藤是荷蘭數學家，1632年與笛卡爾相識，並閲讀了他尚未出版的《幾何》一書，當時覺得難以理解，後來對《幾何》做了重要的註解，翻譯成拉丁文於1649年出版，後來又多次再版，這為笛卡爾座標方法的推廣起到了關鍵作用。更為重要的是，範斯庫藤還給出了座標變換——從一條基線（x軸）到另一條基線變換的代數式，這可能是座標變換的最早工作。

沃利斯是一位英國牧師和數學家，他的主要貢獻在於推動了無窮小微積分的發展。我們在高數中學習到的無窮大的符號∞，就是他發明的，同樣他用1/∞來表示無窮小。沃利斯在座標系上的貢獻在於他引入了負座標，將座標幾何的研究由第一象限推廣到了四個象限，再後來牛頓又用了沃利斯的座標體系，使得解析幾何有了快速的普及。

圖7 範斯庫藤（左）和沃利斯（右）

牛頓在《流數法與無窮級數》一書中還發明瞭新的座標體系。17-18世紀座標系的標準是一個x軸，一個與x軸垂直或成某一角度的y軸。牛頓則採用了固定點和通過該點的直線作標準（類似於極座標），他還採用了雙極座標，點的位置決定於該點到兩個固定點的距離。不過，牛頓的這些成果大約形成於1671年，但出版卻到了1736年。而雅各布.伯努利（JakobI. Bernoulli, 1654-1705）於1691年在《教師學報》上發表了有關極座標的成果，因此通常認為是雅各布首先發明瞭極座標。

17世紀中後期，由拉伊爾（Philippede La Hire, 1640-1718，法國數學家）、約翰.伯努利（JohannBernoulli, 1667-1748）、帕朗（Antoine Parent,1666-1716）、歐拉（Leonhard Paul Euler, 1707-1783）等人的工作，將平面座標系發展為空間三維座標系。

座標系的偉大在於它溝通了幾何與代數，首先，幾何的概念得以用代數表示，幾何的目標也可以通過代數求解獲得。反過來，又可以利用幾何來解釋代數，使代數具有了形象直觀的優勢，還可以藉助幾何去發現那些新的代數結論。拉格朗日曾對這一結合做出過非常高的評價，他説：“只要代數同幾何分道揚鑣，它們的進展就是緩慢的，它們的應用就十分狹窄。但當它們結伴成侶時，它們相互吸取新鮮的活力，就會以快速的步伐走向完善。”

毫無疑問，力學的學習也必須將代數與幾何聯合起來，無論是力學的研究對象（物體位置或形狀）還是研究內容（運動或形變），都離不開座標系，只有在座標系的框架下，實在物體的運動或形變，才抽象成了數學，力學才得以演算。這對於我們的啓示在於：孤立代數與幾何來學習力學就會變得艱難。只有同時將代數和幾何聯合起來，使其在力學的框架內成為伴侶，它們就會相互吸取新鮮活力，學習者就會以較快的步伐進入力學的殿堂！

別忘了，實現這一目標唯有依靠座標！

參考文獻

[1] 莫里斯.克萊因.《古今數學思想》，上海科學技術出版社. 2014.1

[2] 百度、維基等百科知識。

本文經授權轉載自微信公眾號“力學酒吧”，原標題為：《淺談座標系的發展與形成》。