“五家共井”問題的圖形化、Python和APPInventor解法_風聞

文/王德貴

中國古代數學鉅著《九章算數》是張蒼、耿壽昌所撰寫的一部數學專著。其內容十分豐富，總結了戰國、秦、漢時期的數學成就。是當時世界上最簡練有效的應用數學，它的出現標誌中國古代數學形成了完整的體系。其中有一道題是“五家共井”問題，原文如下：

五家共井，甲二綆不足，如乙一綆；乙三綆不足，如丙一綆；丙四綆不足，如丁一綆；丁五綆不足，如戊一綆；戊六綆不足，如甲一綆，皆及。

這道題的白話解釋是：五家合用一口井，甲家的2根井繩和乙家1根井繩總長為井深；乙家的3根井繩和丙家的1根井繩總長為井深；丙家的4根井繩和丁家1根井繩總長為井深；丁家的5根井繩和戊家1根井繩總長為井深；戊家的6根井繩和甲家1根井繩總長為井深。問：井深、各家井繩各多少？（每家的井繩均等長）

下面我們也來分析一下五家共井問題，並用Python、圖形化和APPInventor分別求解。

一、創意來源

在教授學生學習Python四級課程時，合用的練習和案例並不多，於是在搜索案例過程中，看到了這個“五家共井”問題，經過研究發現比較適合用Python四級的知識點來解決，現分享出來。

二、設計思路

這是一個不定方程問題。遇到方程最初的想法還是用枚舉法，在100範圍內運行後，無果。説明最小正整數解，一定比100大，於是擴大範圍到300，結果運行很久也沒有輸出結果，看來運算時間過長了，沒有能等到程序運行出結果。

於是想到庫函數sympy，它是一個符號計算的Python庫。我在文章《阿基米德羣牛問題的分析及Python驗證》裏講過，這裏不再贅述。

通過解方程，得到關係式，從而求出最小正整數解。

在使用Python求解過程中，想試着再用Scratch和APPInventor求解，通過編程，運行，在對比三種代碼之後很有啓發，下面把求解過程分享給大家。

三、程序設計

（一）Python程序設計

1.枚舉法

這是一種最直接是思路，不知道具體結果，那就用枚舉法測試。

由於運行時間較長，運行時將消耗時間打印出來了，此時顯示的是運行了a取值1到10的運行時間222秒。

2.時間複雜度

如果取值範圍在100以內，則時間複雜度是10的10次方，按運行時間算，運行了10個a將近4分鐘，那運行100個a，需要的時間就大約是40分鐘。

當a的取值在1~300時，運行1個a需要的時間將近30分鐘，那300個a就是近150個小時，需要6天多的時間。

這樣長的運行時間完全無法實用，必須通過縮減無效運算來優化程序。改為根據最短的繩子e作為枚舉的主要參數，根據網絡搜索答案，我已經知道e的解小於100，等待一段時間能夠獲得答案。

運行10個e的時間將近是6分鐘，隨e值增大，單次運算時間還會縮短。優化後，運行時間大大縮短了，只需25分鐘左右，已經獲得了一組結果。

我們根據已有答案回推優化程序，最終獲得了結果。但是如果我們不知道答案的範圍，即使只在300範圍內試算，運行也要6個小時左右。枚舉法在面對這樣一個不定方程的情況，如果不知道結果的範圍，那麼運行時間就會非常長！必須去尋找更簡捷的算法。

3.方程解法的程序設計

（1）利用Sympy庫函數先求出不定方程的關係式

運行結果：

因為繩長是整數，所以e一定是76的倍數，因此可以求出最小正整數解：甲:265，乙:191，丙:148，丁:129，戊:76；井深:721。

即甲家井繩長265，乙家井繩長191，丙家井繩長148，丁家井繩長129，戊家井繩長76，井深721。

（二）Scratch程序設計

1.基本思想還是枚舉，利用附加條件循環。

2.程序説明

注意的是，幾個條件都應該是“與”的關係，4個條件截圖不全。如果滿足條件，則説5秒。

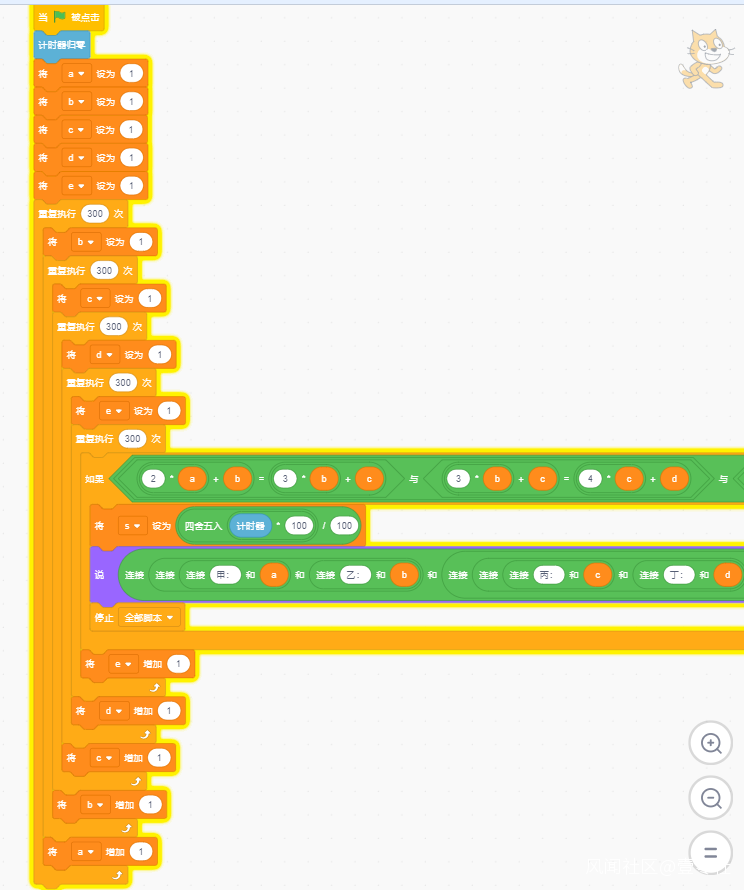程序是5重循環，每個都是300次，a在最外層，運行了1次，就相當於運行了4重300次，就是300×300×300×300次，用了將近24小時，a要是運行300次，總時長則大約需要300天！

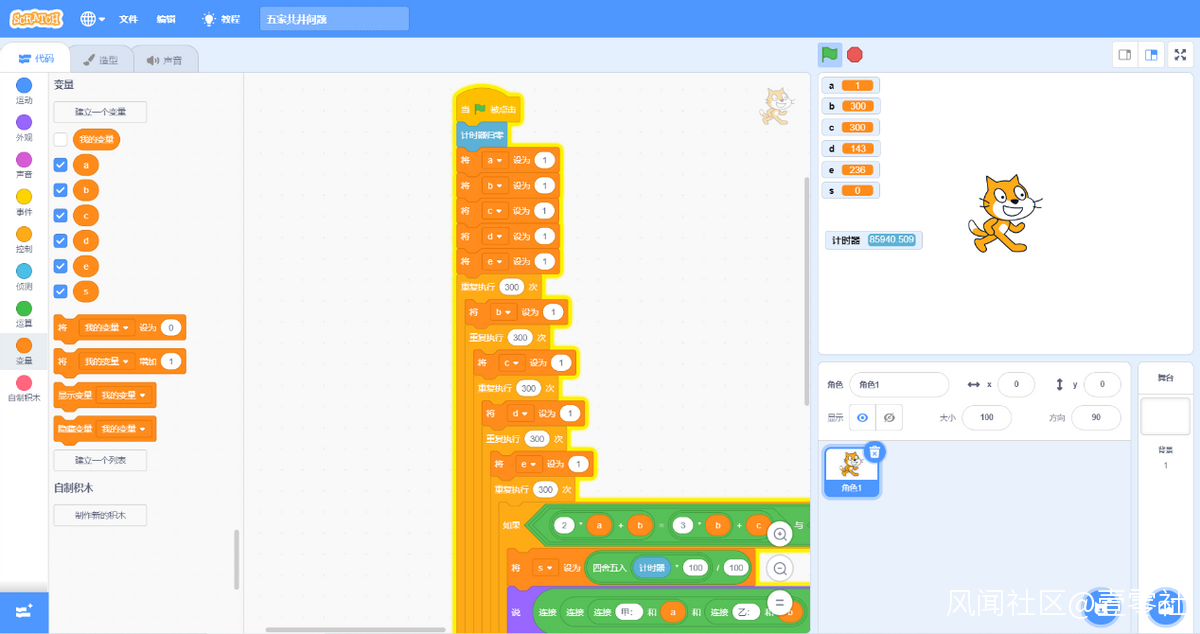3.優化

必須要優化程序，縮小取值範圍。

運行時間6個e，大約3.5小時，但e越大，相對運行時間會越短，所以總運行時間大大縮短了。

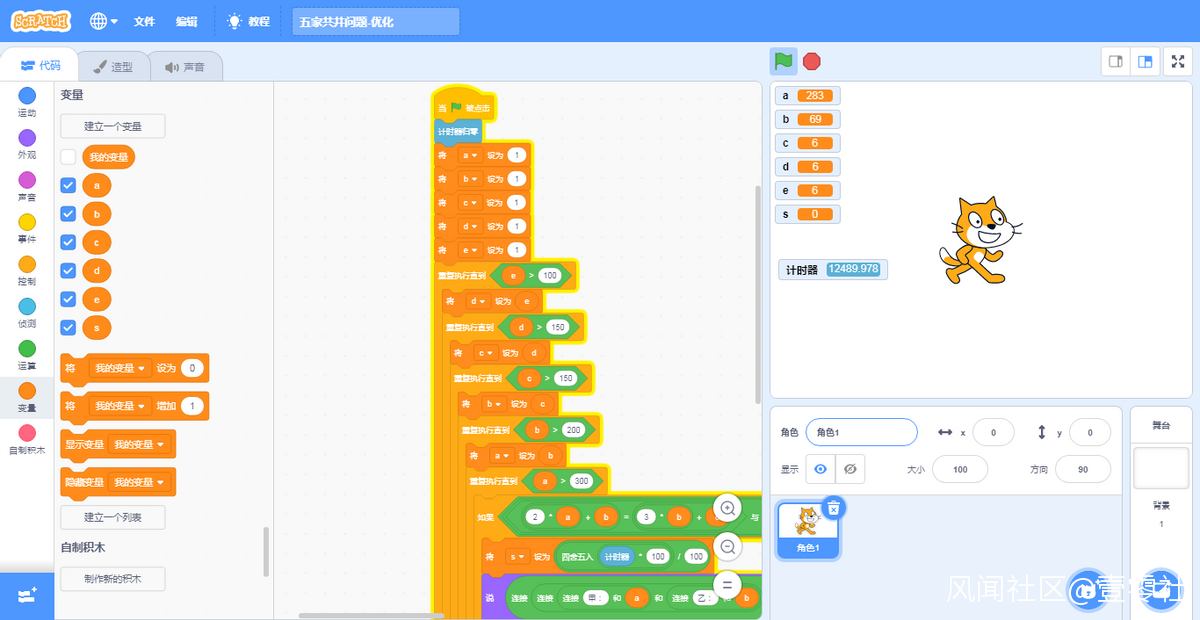但是畢竟時間複雜度太大，Scratch運行效率又太低，總時長還是太大，即使用優化程序測試結果，也需要兩天左右的時間。

（三）APPInventor程序設計

1.設計思路

在Python測試時，在電腦上運行速度還是很快的了，但在手機上運行，則更依賴於手機的配置，明顯感覺運行的很慢很慢。所以加上了直接驗證的程序代碼。

2.程序設計及説明

（1）變量和初始化

變量“枚舉驗證”是使用枚舉法還是驗證數據的轉換開關。

變量“分解列表”是在驗證的時候，分解輸入的數據，並放在列表中，以備程序調用。

初始化程序，一是初始化程序為枚舉狀態，二是提示先選擇使用“枚舉”還是“驗證”。

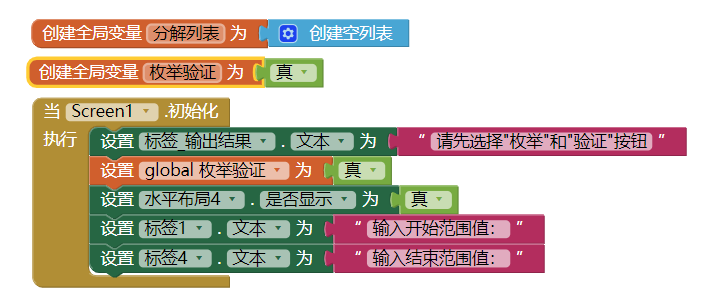（2）枚舉

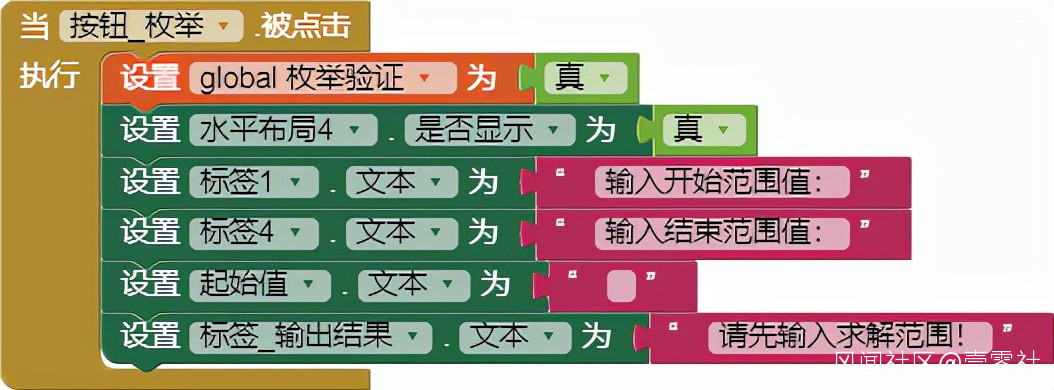點擊“枚舉”按鈕，輸入相關數據。因為驗證時不需要水平佈局4，被程序隱藏，所以使用“枚舉”時，必須讓其顯示出來。

（3）驗證