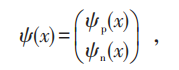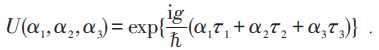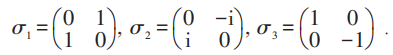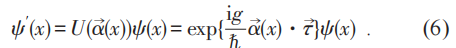楊-米爾斯規範原理和粒子物理標準模型丨慶賀楊振寧先生百歲華誕_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2021-09-23 10:27
撰文 | 吳詠時(猶他大學物理與天文學系)
來源 | 本文選自《物理》2021年第9期
當今世界,諾貝爾獎是公認的科學 (不包括數學) 界的頂尖獎項。當然諾貝爾獎也有遺珠之憾。沒得到諾貝爾獎,不一定意味着水平不夠或貢獻不大。另一方面,得了諾貝爾獎的工作,也不一定就是得獎者最好的工作。這樣的科學家鳳毛麟角,極為罕見。在物理學領域除了愛因斯坦,似乎只有楊振寧先生了。
1957年諾貝爾物理學獎堪稱一個傳奇。該獎頒發給楊振寧和李政道,是因為前一年他們二位合作發表了一篇粒子 (高能) 物理學的文章,質疑公認的左右 (鏡像) 對稱性,提出它可能在弱相互作用中不成立,並建議了若干實驗以進行檢驗。該文發表後受到了高能物理界的普遍冷遇、懷疑甚至否定。一些非常知名的理論物理學家紛紛表示,不相信左右鏡像這樣簡單和基本的操作會導致不同的結果。許多實驗物理學家也不願意浪費精力在這些“註定沒有正面結果”的實驗上。只有吳健雄“獨具慧眼”,立即決定放棄旅行計劃,開始準備開展李—楊文章中建議的一個難度相當大的實驗。到1957年初她的實驗結果明確顯示,左右鏡像對稱性在原子核的貝塔衰變中發生了確鑿的破壞。隨即有關的加速器實驗也很快驗證了類似的現象。消息傳出,立即轟動了全球物理學界。粒子物理學的理論和實驗就此掀開新篇章,出現新高潮。1957年諾貝爾物理學獎也創造了一個新記錄,即獲獎工作的發表到頒獎之間的最短時間差。
這樣的諾貝爾獎,按時下中國網絡的語言,真是“太牛了”。還能有什麼樣的工作或貢獻比這還“牛”?回答是:真的還有。這就是楊-米爾斯的規範場理論和規範原理。在此慶賀楊振寧先生百歲華誕之際,本文意向讀者儘可能通俗地介紹楊先生這個世紀性的偉大貢獻。

20世紀是物理學空前蓬勃、迅猛發展的輝煌世紀。從基礎物理學的角度,人類對於物質結構及其相互作用的動力學,在微觀尺度上推進了至少18個數量級,即10的18次冪。19世紀,物理學的主要進展在熱力學和宏觀電磁學,其實驗基礎都在於日常生活尺度的物體系統;化學已經觸及了原子層級,但令物理學家普遍接受原子存在的實驗尚未出現。到20世紀20年代末,量子力學已經發展成熟,可以用來理解元素週期表和化學的許多細節。至此古希臘關於物質結構的原子學説得到20世紀科學的確證。這是人類科學史上一個歷史性的里程碑。這個里程碑所跨越的尺度是從日常生活 (米的量級) 到原子大小 (0.1 nm),大約是一百億倍。從假説到科學的認知,原子論的成功花費了人類兩千多年的時間。但是,物理學家沒有時間在這一歷史成就前停步,認識自然的下一個挑戰很快就擺在他/她們的面前。1932年中子 (作為原子核的組分粒子) 的發現,開啓了人類邁向亞原子尺度的粒子物理 (或高能物理),研究更深層次的物質結構及其動力學的偉大征程。當時人們沒有料到的是,下一個里程碑的到來是如此之快。2012年歐洲核子研究中心的大型強子對撞機上希格斯粒子的發現,從實驗上補全了粒子物理標準模型的最後一塊拼圖。迄今為止,所有的實驗結果都和標準模型的預言一致,並未發現超出標準模型的確鑿證據。如此人類就達到了科學史上關於物質結構及相互作用動力學的一個新的輝煌的里程碑——粒子物理標準模型的提出和確立。這個里程碑所跨越的尺度是從原子大小 (0.1 nm) 到電子大小的上界 (納米的十億分之一)。所花的時間,距離上一個 (原子論) 里程碑,還不到一個世紀。我下面要講的是,楊—米爾斯規範場理論和規範原理,在實現20世紀後半葉物理學新的里程碑的過程中,起到了巨大的奠基作用。
2 放射性和三大基本作用力
19世紀90年代放射性的發現,特別是放射線的巨大穿透能力,已經預示了比化學能更高的能量尺度。1900年世紀之交,開爾文爵士談到了古典物理學地平線上的兩朵烏雲,它們給20世紀前30年的物理學帶來了相對論和量子論的狂風驟雨。然而無人在那個時候意識到,放射性的發現其實才是定義整個20世紀物理學的隱藏在地平線邊緣的熱帶風暴;風暴過後物理學進入一個新時代,物質結構及其相互作用動力學的微觀尺度,在短短的不到一百年內又推進了近一百億倍。20世紀的第一個十年裏,就已發現放射性物質其實發射出三種射線,用前三個希臘字母,阿爾法、貝塔和伽馬來命名。後來知道阿爾法射線由氦的原子核組成,貝塔射線由電子或其反粒子 (正電子) 組成,而伽馬射線是極高頻率的電磁波 (即光子) 組成。這三種射線都是在原子核內的物理過程產生的,而原子核的大小比原子要小十萬倍,所以説放射性的發現開啓了物理學下一個未知領域的新徵程。更為有趣而絕非巧合的是,放射性的這三種射線恰好對應着自然界的三種基本相互作用或三種基本的力:阿爾法射線對應的是強 (相互作用) 力,把原子核中的質子和中子束縛在一起的力 (也叫做核力) 是它的一種表現;貝塔射線對應於弱 (相互作用) 力,它是導致原子核發射貝塔射線 (弱衰變) 的力;伽馬射線就對應於熟知的電磁 (相互作用) 力。這三種相互作用力和從牛頓時代我們就熟知的引力,合稱物理學中的四大基本 (相互作用) 力。電磁相互作用是麥克斯韋理論的對象。電磁力和引力都是長程相互作用,在我們的日常生活中就可以觀察到。而強力和弱力是所謂的短程力,它的作用力程限於原子核大小的尺度。在20世紀之前,人類不知道這兩種力的存在。它們是20世紀亞原子新物理學的研究對象。
3 提出規範原理的歷史背景
楊—米爾斯的規範場理論文章,發表於1954年。當時正是粒子物理實驗蓬勃發展的初期,各種加速器和新型的探測器飛速發展,陸續投入運行,開啓了粒子物理 (又叫高能物理) 的黃金時代。大量有關新粒子發現的實驗數據和結果層出不窮,激動人心。那時研究粒子物理的理論家,就是在研究分析有關新粒子的實驗數據,從中提煉出新粒子的性質、新的分類模式等等,並提出解釋實驗數據的理論新觀念,發現實驗數據中可能的新問題,提出新的可能的實驗來檢驗理論上的新觀點等等。一句話,當時的粒子理論學家,都是圍繞新粒子的現象學 (即有關新粒子的前沿實驗數據和結果) 開展工作。楊先生當然也不例外。當時他的主要精力也花在這些方面,並已成為粒子物理現象學前沿的一位青年專家。到1954年,他已在美國普林斯頓的高等研究院工作了5年。那年夏天,他去紐約長島布魯克海文國家實驗室 (美國當時的加速器中心之一) 訪問。在那裏,他重新撿起一個在芝加哥大學讀研期間思考過而沒有成功的問題,就是能否推廣電磁場的麥克斯韋理論的問題。當年他開始思考這個問題,也許是好奇心在驅使。但是到此時在布魯克海文,他已精通但不滿意新粒子現象學的研究了,他越發感到了這個問題的重要性和迫切性1):現在已經發現了不少新粒子,未來估計還會發現更多的新粒子。這樣,新粒子之間的相互作用,特別是它們之間的新型未知的強力和弱力,可能會變成理論研究的中心問題。而新粒子一多,它們的動力學運動方程 (或者推導運動方程的最小作用量原理中的作用量) 就必然包含許多項,會變得極其複雜。所以,理論上我們需要一個新的原則去寫新粒子的新的運動方程 (或者作用量)。這在當時是一個相當超前的、思路與眾不同的問題。也許不少習慣於現象學思維的人可能從來沒有想過這個問題。或者偶爾想過但會認為,當時缺乏新粒子相互作用的實驗數據和結果,這個問題不具有解決的實驗基礎和理論基礎,應該在未來積累了相當數量的實驗數據和實驗結果後才提出問題和解決問題。但是,就在那個夏天,和同在一個辦公室的米爾斯合作討論,通過理性的思維,沒有依賴實驗的數據,楊先生就在數學上發明了一個新的方法,從理論上解答了這個問題。這就是非阿貝爾規範場理論和規範原理文章的由來。
4 作為規範理論的麥克斯韋理論
要尋找支配新相互作用動力學的基礎原則,突破口在哪裏?借鑑歷史,借鑑推廣一百年前的麥克斯韋電磁理論,應該是一個好的自然的想法。但即便想到這裏,前進的方向也不是清晰的、唯一的。也許需要先想一想什麼是麥克斯韋理論的實質或精華。這個問題的答案在歷史上、在教科書中也不是唯一的。
最遲20世紀初以來,幾乎所有電磁理論或電動力學的教科書,就是直接從關於電場強度和磁場強度 (統稱電磁場強) 的四個 (包含一階時空偏導數的) 麥克斯韋方程出發。所謂的標量勢ϕ 和矢量勢
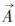
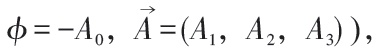
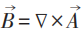
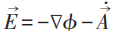
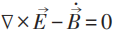
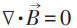
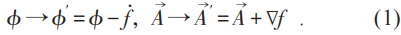
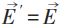
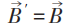
可是,這不是麥克斯韋原始文章和他本人一貫持有的觀點。早年麥克斯韋為完整建立電磁場理論,寫了三篇文章。其第一篇就引入了矢量勢,並在電磁感應 (即沒有電荷) 的情形下寫出了電場強度等於矢量勢的時間導數的方程,以此作為他對法拉第關於電磁感應實驗的直覺的數學表達。通常認為關鍵性的麥克斯韋位移電流是在第二篇文章中引入的。他在第三篇文章中提出了電磁場 (而非分別的電場和磁場) 的統一觀念,從矢量勢和標量勢作為基本量出發,用電磁場能量的表達式作為哈密頓量,從變分原理推導出完整的麥克斯韋方程組。特別是在寫出電荷和電流與電磁場相互作用的哈密頓量時,必須明顯用到電磁勢!在這個理論體系中,電磁勢的規範不變性就有基本的重要性,儘管它們不進入運動方程——麥克斯韋方程組。但是這裏有一個令人困惑之處:不知該怎麼解釋電磁勢規範變換的特定形式和規範不變性的來源。如果採用前面一段的觀點,這個困惑就不存在了。
在經典電磁理論中,這兩種觀點似乎各有千秋。從概念體系的簡單性來看,似乎第一種觀點還多點好處。但是量子力學出來以後就不同了。在量子理論中,電子的波函數ψ(x)可取複數值,其中x是時空點的座標。因為只有波函數模的平方代表幾率密度,我們可以對電子波函數做以下的位相變換:
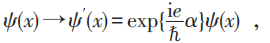
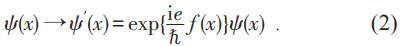
按照定域相互作用原理,電子場有電磁相互作用的理論也應當在電子場的規範變換(2)下不變。但是因為場的時空偏導數不滿足和場同樣的變換,多出了一個附加項:
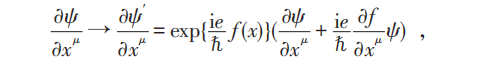
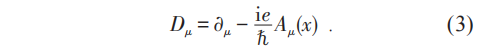
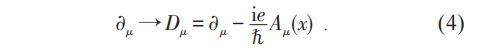
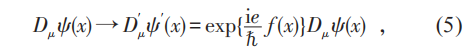
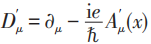
由此可見,經典的麥克斯韋理論中電磁勢的規範變換和規範不變性其實來源於量子理論,即電子 (或任何帶電粒子) 的波函數或者場的(局域)位相變換不變性!後者又是與量子理論中的電荷守恆定律密切相關的深刻的對稱性!楊先生就是抓住了麥克斯韋理論是一個規範場理論的實質,要在對稱性和規範場理論的水平上推廣麥克斯韋理論。
5 楊-米爾斯非阿貝爾規範場理論
在電磁理論中規範羣是U (1)羣;交換兩次規範變換的次序,並不改變結果,這屬於可交換羣,又叫阿貝爾羣。楊—米爾斯所做的推廣就是把規範變換羣推廣到非阿貝爾 (即不可交換的) 羣。考慮最簡單的非阿貝爾羣SU (2)。一個簡單的物理例子,就是核子 (組成原子核的粒子),即質子 (氫原子核) 和中子。它們電荷不同但質量接近,可以考慮為同一核子的兩種不同內部狀態。這很像電子的自旋向上和自旋向下的兩個態,故叫做核子的同位旋態。數學上則用二分量 (列向量) 波函數來描寫,很像一個量子位 (qubit) 的量子態: