在密鋪的瓷磚背後,隱藏着令人毛骨悚然的幻影...._風聞
中科院物理所-中科院物理所官方账号-2021-09-28 22:39
原創:中科院物理所
如果你擅長利用圓規和直尺創造各種神奇的圖案,你會發現各種邊為弧形的有趣圖形。讓我們看看弧形構成的簡單幾何形狀吧。
一個簡單的例子是由等邊三角形的頂點構成的曲邊三角形(Reuleauxtriangle)(如圖一所示)。依次將圓規頂點放在三個頂點上,然後繪製連接剩餘兩個頂點的圓弧,這樣便得到了三段圓弧組成的曲邊三角形。三條弧所對應的圓周角都為 60° 。曲邊三角形是唯一一個邊由弧形構成,且弧形的中心為頂點的曲邊形狀。
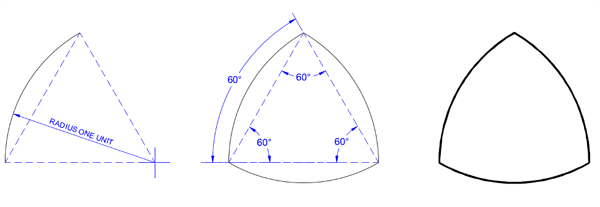
圖一:曲邊三角由等邊三角構成。
通常,圓弧的形狀主要由兩條信息定義:圓的半徑和圓弧角。我們可以找到圓弧中心與圖形頂點存在有趣關係的其他弧邊圖形,比如圖二中的三種圖形。從圖形頂點出發繪畫新的圓弧,得到的圖形與原始圖形之間存在旋轉或鏡像關係。此外,原始圖形中每段圓弧對應的的圓心同樣位於新圖形的頂點,因此不難看出這個繪製的過程是可逆的。
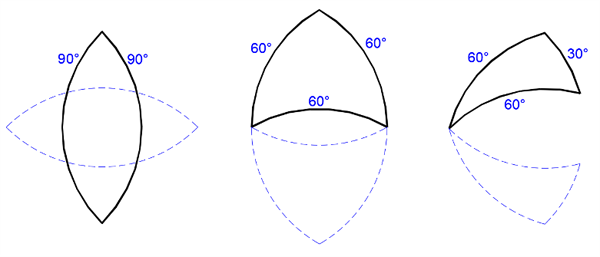
圖二:存在“幻影”的三種形狀
新繪製的圖形被稱為原始圖形的“幻影”,它**是由原始圖形頂點繪製的圓弧構成的,它與原始圖形形狀一致,但存在旋轉或者鏡像的關係。**上面提到的曲邊三角形是自參照的:它是自身的幻影。你可能覺得這些幻影跟隨着原始形狀虛無縹緲地存在着,就像一種幽靈般的存在。
當數學家們遇到二維圖形時,他們經常會問自己一個問題:類似於正方形瓷磚可以鋪滿整個廣場,如果給你這個形狀的瓷磚,你能用它來平鋪整個平面嗎?
對於目前提到的這四種形狀而言,答案是“不”,這幾種形狀都不能單獨平鋪一個完整的平面。用弧邊圖形鋪滿平面需要等量的凹面和凸面圓弧。
接下來,讓我們看看第五種形狀,或者説一類形狀。
三曲線
鏡片是一種最簡單的幾何形狀,它由兩條相同的弧線拼接而成,假設弧線的半徑為 1 ,鏡片就可以簡單得用弧的角度來描述。在弧線上取一點,將弧線分成兩部分,然後每部分都可以製作一個鏡片,從大的鏡片裏面減去兩個小的鏡片,就會得到一個不同尋常的三曲線的形狀。
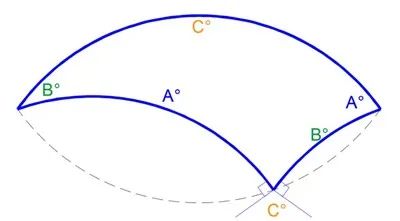
圖三:三曲線幾何圖形
**任意的三曲線都能週期性地平鋪:**將三曲線圖形沿着某個方向平鋪,就會得到如圖四的形狀。
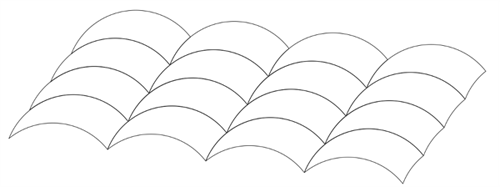
圖四:週期平鋪
如果構成三曲線的弧度的角度是 360° 的因數,而且弧線滿足特殊的比例(比如 1:2:3 ),那麼三曲線就會具有徑向和非週期性質的平鋪屬性,這個性質非常有趣,你可以自制這個拼圖進行嘗試。

1

2
圖五:拼圖
每個三曲線都可以升序的三個弧角來形容,其中兩個凹弧的和為大的凸弧的值。迄今為止製作的拼圖多是用 30°-60°-90°(圖五1)或 36°-72°-108° 弧度(圖五2)的三曲線製成,當然還可以用其他角度或者比例的圖。除了單面平鋪之外,還可以用多種類型的方式平鋪。
三曲線的幻影
三曲線的幻影是什麼樣子的?每個三曲線都存在對應的幻影,將三曲線按照一個固定的旋轉中心旋轉 180° 得到其幻影,根據三曲線的不同,幻影可能會跟原形狀分離,也可能會重疊。
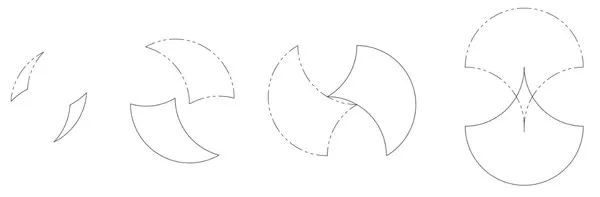
圖六:一些三曲線的幻影
為了確定或者可視化三曲線的幻影,只需要三曲線旋轉半圈,再將連接兩個凹面的那個頂點定位在原始大圓弧的中心。例如,對於任何具有 180° 大弧的三曲線,無論兩個較小的弧線如何,幻影的中間頂點都位於半圓的中心。
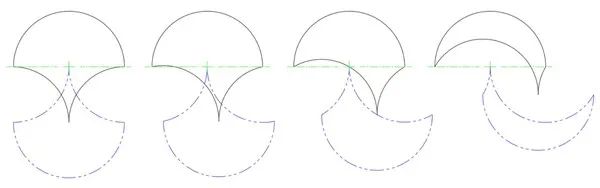
圖七:一些具有180°大弧的三曲線以及幻影
對於一些對稱的三曲線,幻影是原始形狀旋轉 180° 之後的樣子,也是初始圖像沿原始三曲線對稱軸的鏡像對稱圖案。
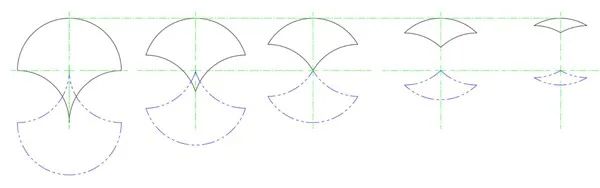
圖八:一些對稱的三曲線和其幻影。
用幻影進行平鋪
當利用三曲線平鋪平面時,觀察平鋪三曲線的幻影,會發現幻影也在進行平鋪。正如預測的那樣,週期平鋪也會使得幻影週期排列。

圖九:帶有幻影的週期性平鋪
但是,仔細觀察這個形狀,會發現事情不是那麼簡單的。在圖九中,你必須得仔細觀察才能發現哪個幻影跟原始形狀是搭配的。你會發現,除了整組原始三曲線發生了 180° 旋轉之外,幻影位置還變了。如果將幻影位置逆旋轉 180° 會發現這組排列位置變了。
如果用不同大小的三曲線,這一現象會更加明顯。在圖十中,可以看出幻影不僅僅旋轉了 180° ,而且位於彼此對立的兩邊,不再共享一條弧。
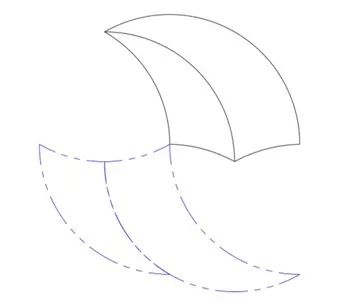
圖十:轉置的幻影
這種怪異的行為也出現在徑向的平鋪中,對於圖十一來説,星星或者花瓣形狀的三曲線的幻影,是一個環形。
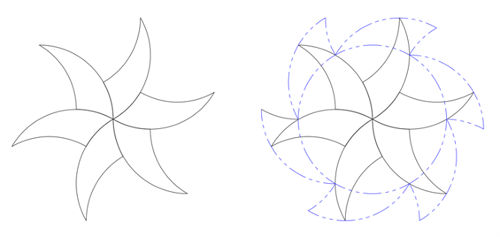
圖十一:帶有環形幻影的花型三曲線
因此,當利用三曲線進行平鋪時,其對應的幻影也以一種非直觀的、轉置的方式來平鋪。仔細想想,當你將三曲線形狀的材料進行平鋪時,其對應的幻影也在一種奇怪的方式進行平鋪,這件事讓人感到毛骨悚然。
用三曲線填充特定的形狀會發生什麼?
填充圓形
假如有任意一個鏡片形狀的物體,用三曲線來對其進行填充可以得到兩個較小的鏡片。每個小鏡片可以被兩個更小的鏡片和一個三曲線填充。以此類推,任何鏡片都可以用一系列越來越小的鏡片填充。這種情況也適用於圓,因為圓同樣是一種鏡片。
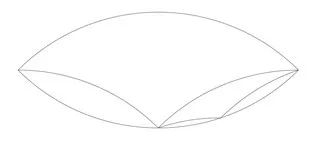
圖十二:鏡片的層次
填充圓的方法有許多,而這裏介紹一種普通的方法。首先用最大的三曲線來進行填充,然後向下尋找次一級最大的圓弧進行填充,以此類推,將“剩餘鏡片”留在下半部分的周邊。然後,這些剩餘鏡片被逐漸變小的三曲線填充,直至變為無限的序列。
這裏列舉四種方法,每種方法的介紹僅深入到一定的填充程度。
方案 A 是利用對稱的方法填充,每一層的弧線都一分為二,如下圖所示:第一個三曲線弧角為 90°-90°-180°,第二層是 45°-45°-90° ,第三層是 22.5°-22.5°-45° 。
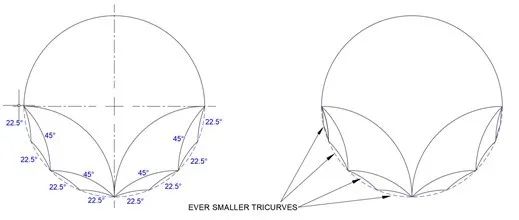
圖十三:A: 圓的對稱填充
或者,可以將三曲線最小的弧角保持為 22.5° ,利用從同一點出發的圓弧(圖十四左),或者大的三曲線交錯的形式(圖十四右)來完成填充。
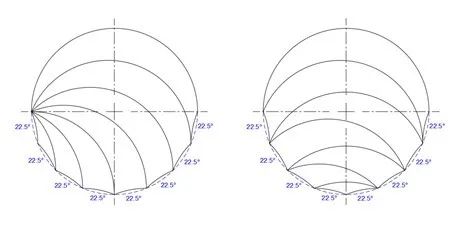
圖十四:方案 B 和 C 。
這兩例都用了七個三曲線,只是排列方式不同,兩種情況下頂部的三曲線都是 22.5°-157.5°-180° 。同時,以上三種填充方式,未填充的下半周的鏡片數量和尺寸都相同,恰好是八個 22.5° 的鏡片,這些鏡片也最終會用無限的小的三曲線來進行填充。
方案 D 是方案 B 的變體,只不過是用更細的三曲線進行的填充。剛開始,我們可以用 5° 的小角度(5°的小圓弧)來進行填充,最大的三曲線是 5°-175°-180° 。
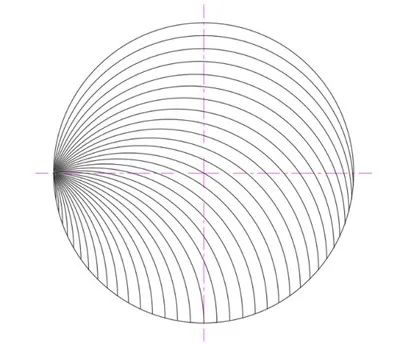
圖十五:細的三曲線
圖十五沒有顯示圓下半部分的圓弧和鏡片,因為將其做的很小,所以在這個尺度下很難區分。**隨着小圓弧的角度大小趨近於 0° ,主要的三曲線的會趨近於無限多,而剩餘要填充的鏡片也會無限小。**這似乎是最簡單,也是最優雅的填充圓的方法。
此時,填充三曲線的幻影是什麼樣子的?
考慮上面 A-C 三種情況下的幻影,如圖十六所示。
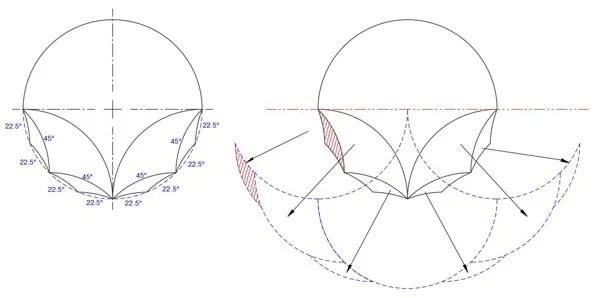
圖十六:方案 A 的幻影
方案 A 中對稱的三曲線填充比較簡單,每個幻影都是原始圖形的鏡面對稱,頂點在原始圖形的對稱軸上。方案 B 和 C 的幻影如圖十七所示。
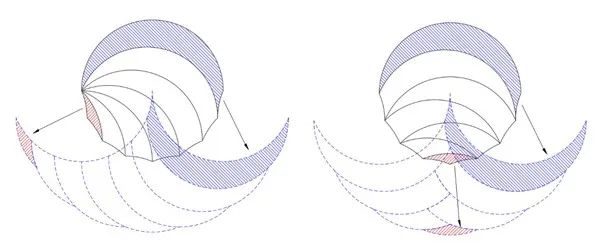
圖十七:B和C的幻影
可以發現,三種情況生成的幻影都是一樣的,這是為什麼呢?
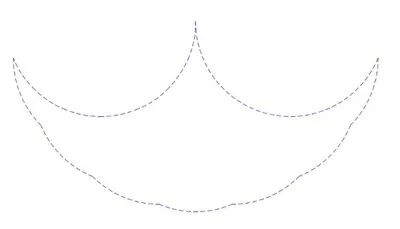
圖十八:幻影的神秘輪廓
如果繼續填充圖形剩餘的鏡片,會發生什麼?以方案 A 為例,繼續填充的圖形如圖十九所示。
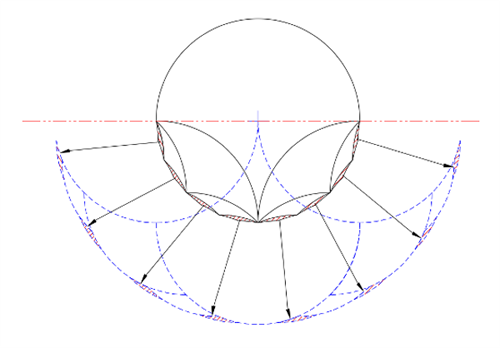
圖十九:填補剩餘“裂縫”
對於 A-C 繼續進行填充得到的結果是一樣的。對於每種填充方式,幻影填充新形狀外側的凸起之間的縫隙,或者向上延伸尖端。極限形狀是一個半徑為原始圓的直徑的半圓,減去兩個原始的半圓形狀,如圖二十所示。無論用對稱還是不對稱的三曲線對圓進行填充,其幻影得到的結果是一樣的。因此,幻影創造並填充了一個新的形狀:一個對稱的方圓(arbelos,由三個半圓組成的形狀)。
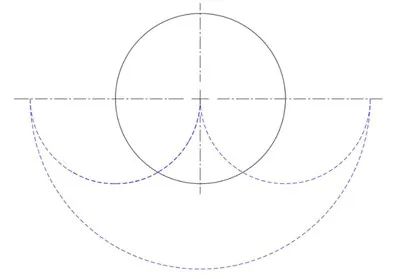
圖二十:產生的超級幻影
當方案 D 採用同樣的極限情況時,得到的結果相同:隨着填充的三曲線的數量接近無限大,幻影的形狀接近對稱的方圓。
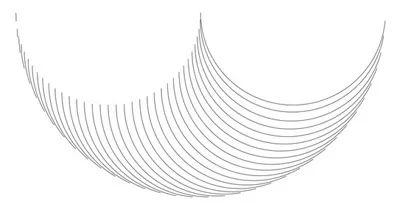
圖二十一:方案D的轉換
我們可以反過來做,雖然會有點困難:我們可以從對稱的方圓開始,用無窮的三曲線填充它,然後製作這些三曲線的幻影,最後回到填充圓。無論圓是如何用三曲線填充的,這都是正確的。因為**對稱的方圓是填充圓中所有幻影三曲線的並集,所以我們稱對稱的方圓是圓的超級幻影。反之亦然,因為它是可逆的。**因此,一個形狀的超級幻影是該形狀的填充三曲線的幻影結合的輪廓。
回到鏡片
將上面對圓的操作同樣作用到鏡片上。回到方案B,從整個圓中找到一個鏡片(橙色輪廓),其對應的超級幻影圖二十二所示。
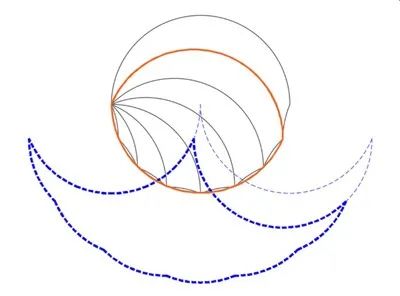
圖二十二:子鏡片和其超級幻影
更多子分級的鏡片和其幻影。
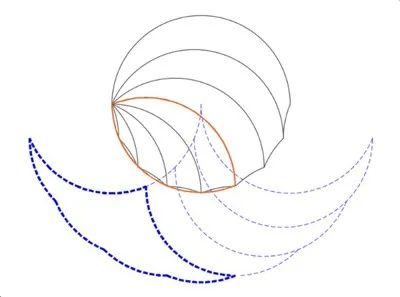
圖二十三:另一級別的鏡片和它的超級幻影
如果將不同級別的鏡片並排比對,會發現圖二十四的結果。
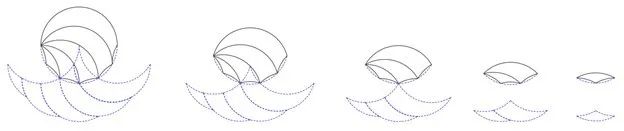
圖二十四:方案B填充下不同鏡片及其幻影
用三曲線填充鏡片的方法還有很多,我們也可以用小於 22.5° 的鏡片進行填充。就像我們填充圓時所做的那樣,可以將其填充到極限。最後,對於任何鏡片,超級幻影都是一個廣義對稱的方圓,而其中弧度可能會小於 180° 。這裏有一個由三條角度相同的圓弧構成的初始鏡片,鏡片跟其幻影的關係如圖二十五所示。
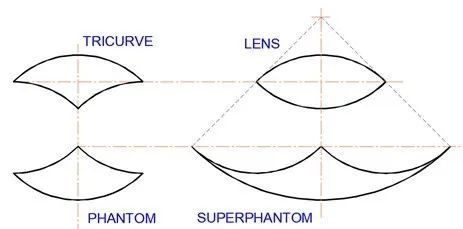
圖二十五:鏡片和其超級幻影
減去超級幻影
最後,我們注意到鏡片和超級幻影可以從更大的鏡片和超級幻影中減去。在下面的圖中,在原始鏡片(左)中移除了兩個較小的鏡片(中),從而得到了一個三曲線(右),而超級幻影在這個過程中相應地發生了改變。
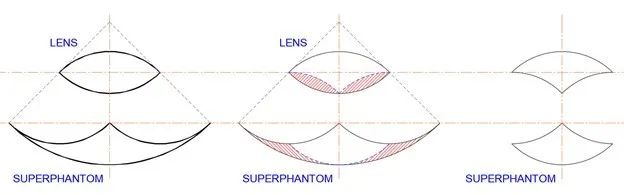
圖二十六:移除兩個鏡片
再來看另一個例子,從一個圓中減去兩個鏡片,對應的超級幻影則是從完全對稱的方圓中減去兩個廣義對稱的方圓。
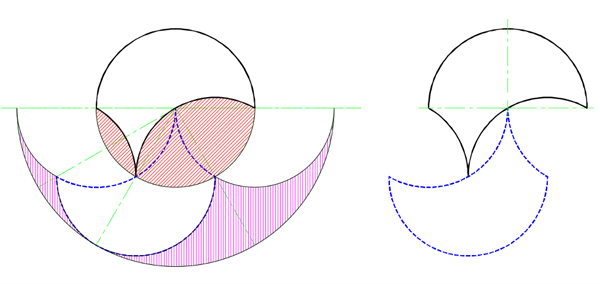
圖二十七:從圓中減去兩個鏡片
你可能會注意到,在上面的兩幅圖中,兩個較小的鏡片從較大的鏡片上取下,剩下的形成了一個三曲線。由此產生的超級幻影也是該三曲線的幻影。事實證明,對於任何三曲線,超級幻影都和幻影一樣!
這篇文章從簡單的直尺和圓規開始,從圓弧到鏡片,到三曲線,到幻影,到填充圓,超級幻影再到方圓。但還可以再進一步,把圓圈和其超級幻影結合起來,你快動手試一試吧~
作者:Tim Lexen
翻譯:Nuor
審校:C&C
原文鏈接:
https://plus.maths.org/content/ghosts-tiles https://plus.maths.org/content/ghosts-tiles-continued