2021年諾獎得主Giorgio Parisi的集體行為研究_風聞
返朴-返朴官方账号-关注返朴（ID：fanpu2019）,阅读更多！2021-10-17 14:45
對一個鳥羣而言，最智能的狀態應該是某種“團結緊張”的狀態。這種狀態恰好處在“有序”與“無序”之間，類似於相變的臨界點處，此時，一個羣體既能保持其穩定性，又能保證個體的信息在羣體中有效地傳遞。
撰文 | 傅渥成
圖1. 魚羣的集體運動
最早嘗試研究動物集體運動的人是日本的魚類學家，他們早在六七十年代就提出了魚類集體運動中的基本原則，然而因為太過於超前，他們又只用日語發文章，這些研究並沒有得到重視。而到了八十年代，隨着計算機科技的發展，動物集體運動的原則重新被計算機科學家 Reynolds 發現了，這一工作發表在計算機圖形學的會議上。我們今天見到的許多動畫、電影中的大場面，通常都是用類似的方法讓計算機生成的。在這篇文章中，Reynolds 總結了羣體運動模擬的幾個核心的要點：
體積排斥：每個模擬的個體（boid）都會佔據一定的體積，而這些體積永遠不會相交，即每個個體都會避免與最近的個體發生碰撞。速度對齊：每個個體與其近鄰的個體們保持速度同步。聚集傾向：粒子不會傾向於獨立行動（粒子羣保持維持），每個個體會盡量與附近個體靠近，避免被孤立。
有了這些基本要點，我們就確定了集體運動中個體之間的相互作用，當許許多多的個體聚集在一起時，動物的羣體就可以產生各種各樣複雜的運動模式。我們已經知道，在鳥羣中，相鄰的鳥的速度會趨向於平行，但僅僅知道這些還並不夠，我們想知道這種相鄰的鳥與鳥的相互作用究竟會在多大的範圍內影響鳥羣的運動。事實上，雖然每個鳥只受到附近較少的幾個近鄰的影響，但這種影響竟然可以遍及整個羣體！
圖2.2021年諾貝爾物理學獎三位得主。一半獎金授予了Giorgio Parisi，表彰其對複雜系統的開創性研究
2021年諾貝爾獎得主 Parisi 曾經與 Cavagna 等人合作，對鳥羣的運動進行了長期的觀察，他們用兩個攝像機拍攝同一個鳥羣，從而重建出鳥運動的三維座標（這與我們在電影院觀看 3D 電影的基本原理是相同的），然後從這樣一個 3D 的影片中算出來各個時刻，羣體中的各只鳥分別處在怎樣的位置，又根據相鄰各幀畫面，計算出鳥的速度，從這樣的視頻中我們可以得到很多有用的信息，這裏我們介紹其中最有趣的“臨界”特徵。
論文題目：
Scale-free correlations in starling flocks
論文地址：
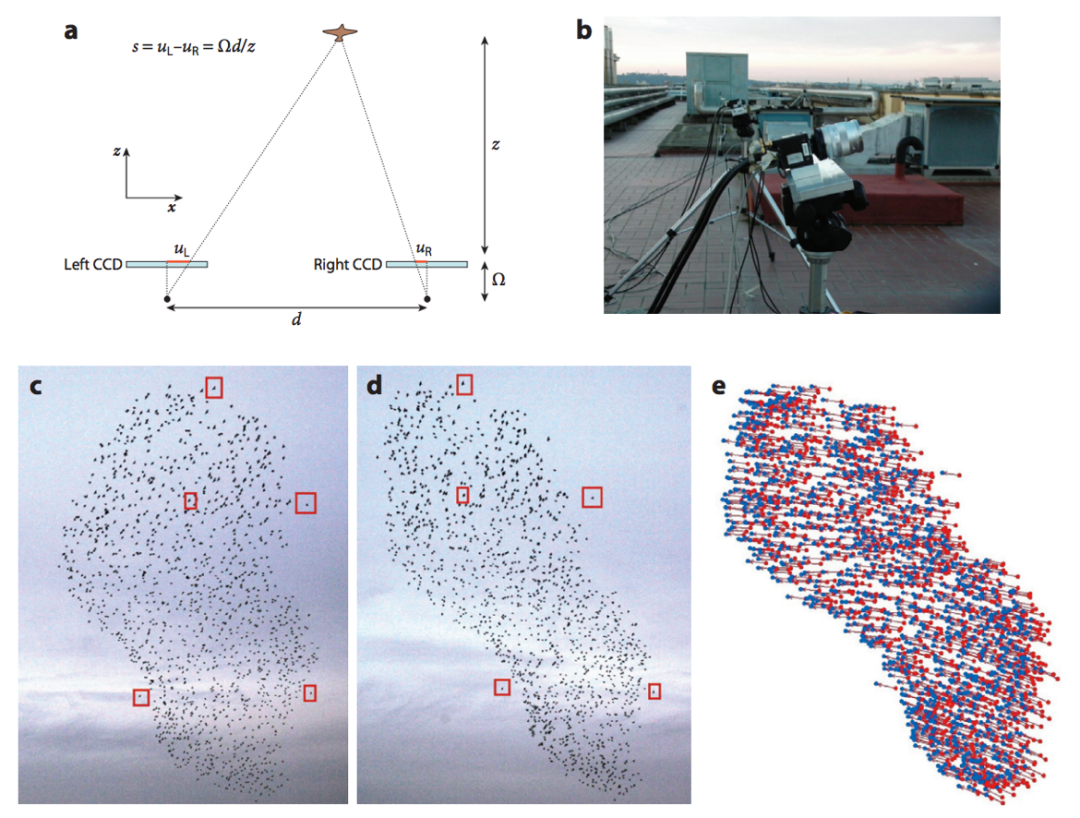圖3. 實驗裝置及原理圖
一隻鳥因為各種不確定性因素、外界刺激或者突發奇想，稍稍改變了它的運動方向，那麼它的這種行為能影響到多大的範圍呢？這裏的“影響力範圍”就是“關聯長度”。分析關聯，對於物理問題的分析非常重要，文小剛教授曾經在他的《量子多體理論》中提到：“我們可以測量的其實只是關聯函數。我們不禁很想用關聯函數來定義世界上的物理理論，關聯函數可能就代表着我們世界的真實。”在舍恩伯格的《大數據時代》中，“關聯”（相關）跟“因果”是相對的，在物理學裏，直接的相互作用就對應於“因果”，例如兩隻相鄰的鳥為了防止相互碰撞而產生相互排斥的效果，如果不是“因為”鳥 A 如此靠近，鳥 B 也不至於要到改變運動方向的“結果”；而“關聯”則更多的是因為間接的相互作用所造成的，例如處在鳥羣的外圍、直接觀察到了捕食者的鳥跟位於鳥羣另一側的鳥之間顯然不存在直接的相互作用，但它們的運動依然能相互影響，這即為“關聯”。這種關聯性就可以用“關聯函數”來描述。
怎樣用關聯函數描述鳥羣中不同個體之間運動情況的關聯呢？儘管整個鳥羣在朝着某一個共同方向以平均速度 v 運動，但鳥羣中的諸多個體可能自己的運動速度會與這個平均速度的方向或大小有所偏離。我們可以計算鳥的速度偏差之間的關聯，即考慮在鳥羣中挑出距離為 r 的兩隻鳥（i, j），讓它們各自真實的運動速度分別減去平均速度，得到相對速度，然後計算相對速度的內積，再然後，把所有這樣的距離為 r 的鳥都選出來計算內積，這一內積的平均值即為 C(r)。
如圖 4 中（a）（b）所示，距離很近的兩個鳥當然更傾向於同進退（關聯接近 1，不然就會撞在一起），而距離遠到一定的程度，C(r) 的值會降低到 0，在鳥羣的運動問題中我們把 C(r) = 0 時 r 的取值 ξ 定義為“關聯長度”，而當 r>ξ 時，鳥與鳥的速度關聯可能為負，即這些鳥傾向於往相反的方向運動。如果還對速度的大小和方向的漲落進行進一步的區分，可以得到如圖 4 所示的結果。如圖 4 的（c）（d）中所示，對於不同大小的鳥羣，其關聯長度與鳥羣的尺寸成正比，因而這種關聯可以遍及整個鳥羣。在臨界態，對於無限大的系統，關聯長度甚至可以趨向於無窮。
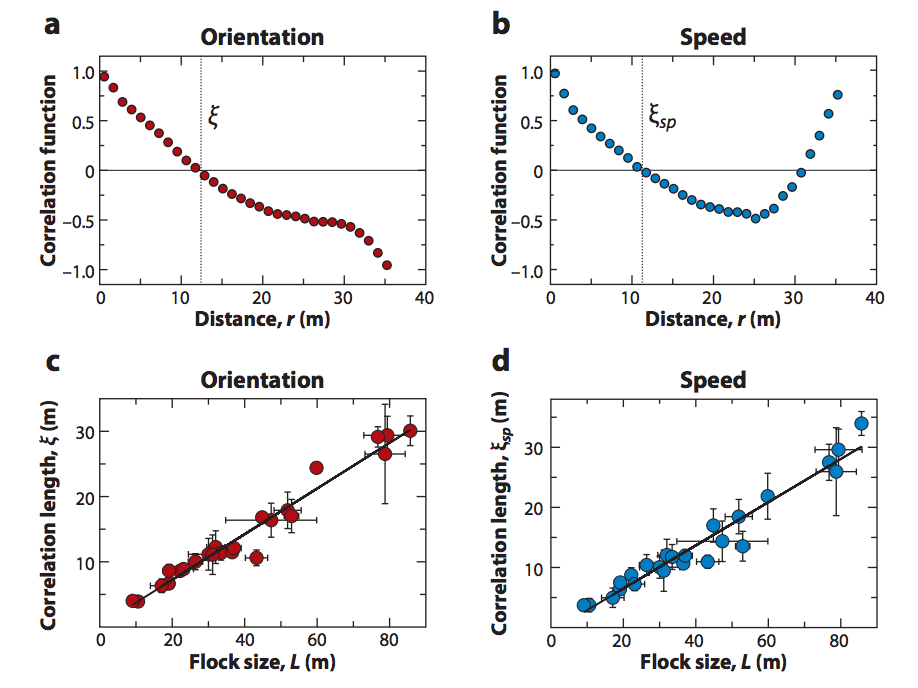圖4. 鳥羣運動的（速度漲落）關聯函數。這裏的圖 （a）和（c）對應的是速度方向的關聯，圖 （b）和（d）對應的是速度大小的關聯。而圖（a）（b）計算的是關聯函數的距離依賴關係，圖（c）（d）計算的是關聯長度隨着鳥羣大小的變化關係，從圖中可以看到關聯長度與鳥羣的大小是成正比的。
直觀地看，關聯函數可以理解成一種”影響力”，在一個鳥羣中，平均地來看，較長的關聯長度意味着各個鳥都有較大的影響力範圍。如果鳥羣在運動中沒有達到臨界，那麼對於不同大小的鳥羣而言，關聯長度會更像是一個常數，這看起來是自然的，因為在描述集體運動的各類計算模型中，每個鳥的速度只與跟它們距離小於一定值的鳥的速度存在”相互作用”。在沒有到達”臨界”的情況下，在一個有 100 只鳥的鳥羣中，一隻鳥運動方向的改變，大概會影響與這隻鳥距離小於 1 米範圍內的其它同類，如果是更大規模的鳥羣，如 1000 只鳥的羣體，一隻鳥的“影響力”範圍仍然會是大約 1 米。然而如果鳥羣達到了”臨界”，讓人感覺意外的事實發生了，正如我們在各種物理系統的臨界態中所看到的那樣，這種“影響力”就可能會變得非常長。
“影響力”變長並不是一件簡單的事情。不同的體系中可能出現非常類似的“長程關聯”現象，但這些長程關聯出現的原因可能並不相同。在有的體系中，因為存在“領導人”的角色，而所有個體都無比尊崇領導人的一切決定，因此個體間就出現了這種長程關聯。而有的體系或許因為一些組織形式使它們產生了這種長程關聯，例如 Ising 模型所描述的磁體當其位於相變臨界點附近時，這種長程關聯就會存在，其關聯長度會趨向於無窮。不管產生長程關聯的原因如何，從觀測和統計的角度來看，在系統中出現了某種與系統本身尺寸無關的關聯性，這種長程關聯也被叫做“無標度的關聯”（scale-free correlation）。處在臨界態的系統普遍具有這種無標度的關聯。雖然每個鳥只受到附近較少的幾個近鄰的影響（保持速度的一致性），但在羣體中任意一隻鳥的速度如果發生變化（這種變化可能是由於發現了障礙物或者天敵所造成的），那麼這種速度的變化不只會對這隻鳥的鄰居們產生影響，而且可以遍及整個羣體。這種無標度的長程關聯正是鳥羣“敏感性”的來源。
有意思的是，但在各種不同的生物系統中，這種長程關聯竟然也普遍存在。為什麼鳥羣傾向於在臨界點附近工作呢？如果一個鳥羣過於團結（類似於有序的固體），那麼它們將會盲目地朝着一個方向飛，此時，如果有一個個體注意到前方的障礙物，在其它個體沒有看到障礙物的情況下，他將沒有辦法阻礙集體的力量，最終，整個羣體將撞上障礙物；而如果一個鳥羣過於鬆散（類似於無序的氣體），那麼它們就沒有辦法組織起來完成那些個體無法實現的行為（如一起對抗天敵）。對一個鳥羣而言，最智能的狀態應該是某種“團結緊張”的狀態。這種狀態恰好處在“有序”與“無序”之間，類似於相變的臨界點處，此時，一個羣體既能保持其穩定性，又能保證個體的信息在羣體中有效地傳遞。
臨界的特徵對生物羣體來説有着重要的意義，在草原上遷徙的羊羣，天空中飛翔的鳥羣，河流中洄游的魚羣都常常會遇到相似的問題，因為捕食者可能會從各個方向靠近來捕獵羣體中的某些個體，甚至有的時候捕食者也會展開羣體的攻勢——這些情況就像自習的教室外有老師走過一樣危險。這時候，這些動物們會需要快速做出反應，於是我們看到鳥羣在空中不斷變換着形狀，羊羣突然聚集在一起，或者魚羣組合成一條看起來更大的魚的樣子，這種靈活應變的能力體現了生物的某種集體智能，這也是簡單的有序或者無序態難以實現的。
大腦的工作原理與鳥羣也有相似之處。在大腦中，信息的有效整合需要有“長程關聯”的存在。近年來，隨着各種實驗技術的發展，我們可以用功能性核磁共振（fMRI）等實驗直接測量大腦皮層中不同區域之間神經信號發放之間的關聯，這種關聯也是長程的，並且大腦皮層中距離距離較遠的區域的放電情況還可能出現反關聯，這些性質表明，大腦也是處在臨界態的。這種特性幫助大腦始終保持在最佳的工作狀態——穩定性與可塑性的最佳平衡。幸運的是，我們的大腦在穩定性和可塑性之間達成了一種巧妙的平衡，我們的大腦恰好處在一個最具適應性的臨界點上。
本文經授權轉載自微信公眾號“集智俱樂部”。