MIT副教授趙宇飛團隊登數學四大頂刊，華人作者中兩位是本科生，最小的是00後_風聞

　　夢晨 蕭簫 發自 凹非寺

　　量子位 報道 | 公眾號 QbitAI

　　你能想象，一個等角線問題，竟然困擾了數學家們70餘年？

　　等角線的定義很簡單，穿過一個點的一組直線，任2條之間夾角都相等就是等角線。

　　比如在二維平面相互垂直的兩條直線或，或相互成60度角的3條直線。

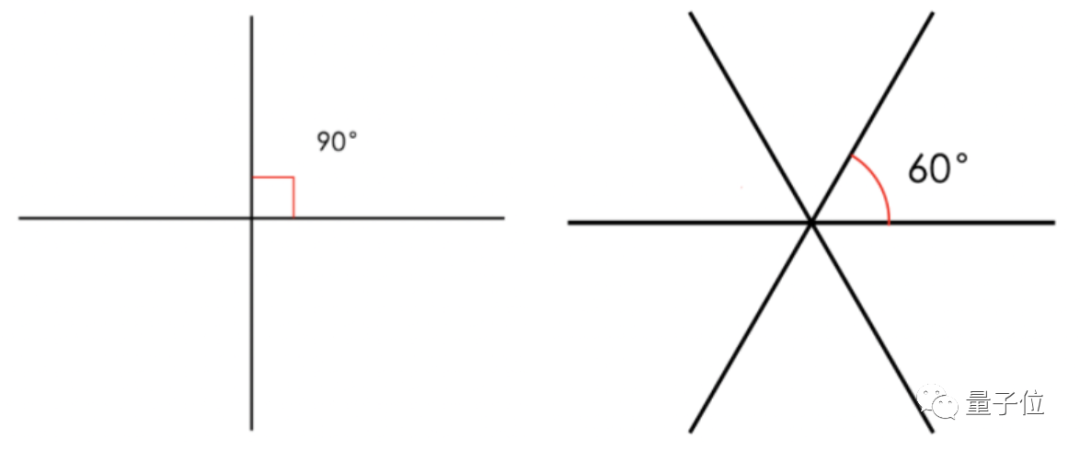
　　3條直線形成的6個60度夾角，也剛好把一個二維空間分成6部分，合起來就是360度。

　　3也就是二維空間中等角線數量的最大值了，很極限的滿足了任意兩條直線之間夾角都相等這個條件。

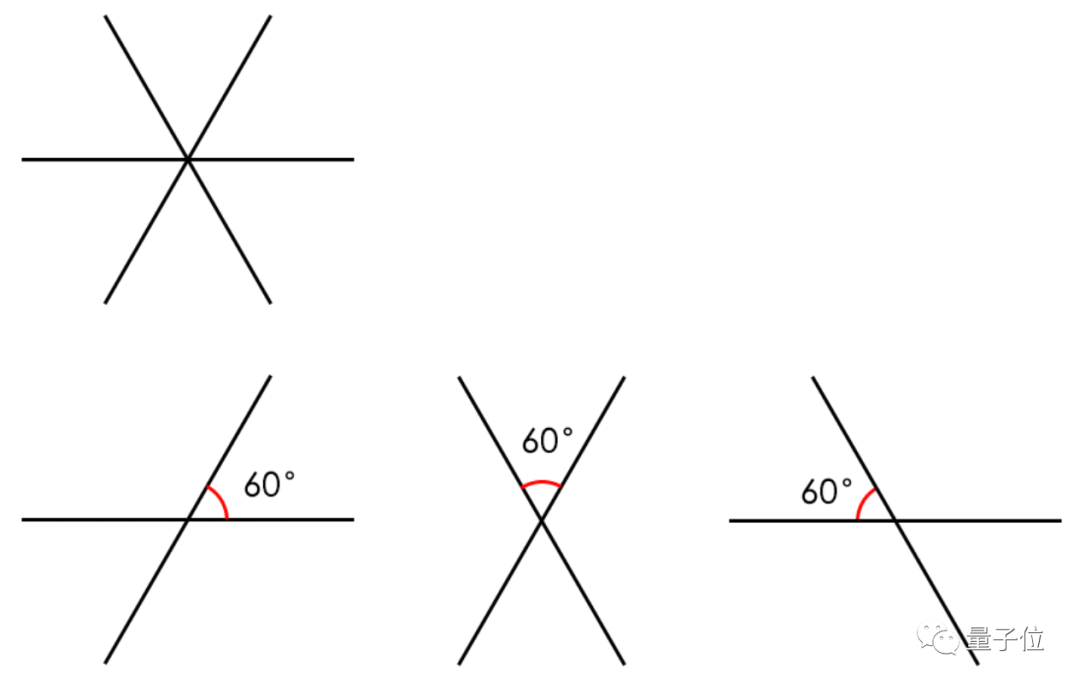
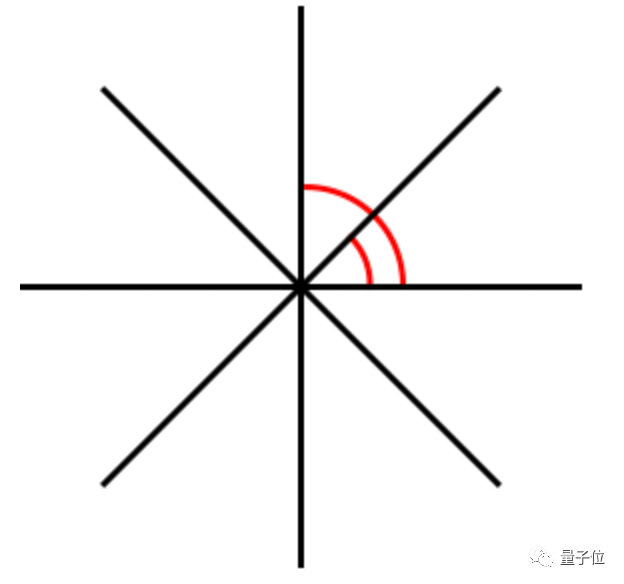
　　如果再多一條直線，無論怎麼擺條件都無法成立。

　　到了3維空間，情況要複雜一些，不過通過想象和畫圖也可以找出，等角線最多可以有6條，此時的夾角是63.4度。

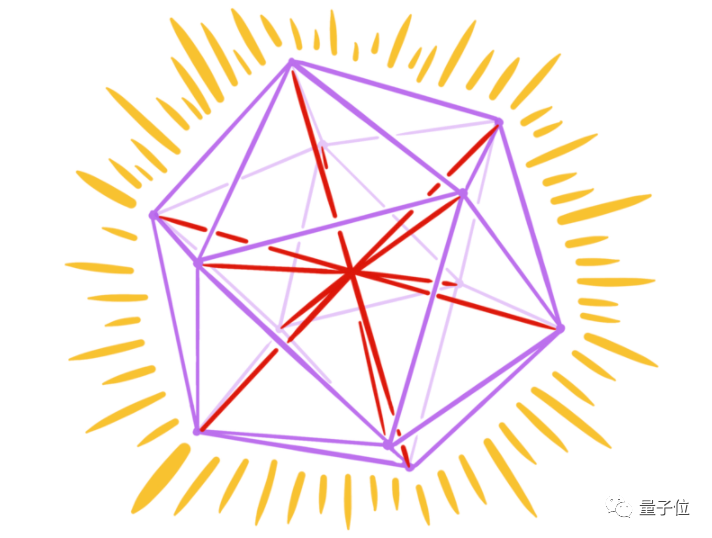
　　****△圖源：MIT 作者：Zilin Jiang

　　到這裏都還不難，然而推廣到4維、5維、6維……N維呢？

　　高維空間等角線數量最大值問題，一困擾數學家們就是幾十年。

　　科學家們長久以來只能給出一個範圍，而沒辦法算出精確的數值。

　　現在，這一難題終於被MIT副教授趙宇飛帶領團隊突破了，已被四大頂刊之一的《數學年刊》接受，預計於2022年的第一期發表。

　　普林斯頓大學教授Noga Alon對此評價：

　　這是一個美妙的結果，為幾何極值中一個已經被廣泛研究的問題提供了驚人的答案。

　　火星通信就用上了

　　在解答問題前，你可能有一個疑惑，研究這個做什麼？

　　其實，尋找高維空間中的等角線最大值不僅有理論數學上的意義，也有一定的應用價值。

　　特別是嘈雜通信環境下的信息編碼和傳輸問題。

　　比如正在遙遠火星上探索的天問一號和祝融號，它們傳回地球的信號該如何保證準確性？

　　信號在如此長的距離中傳輸，不可避免會遇到許多噪聲。

　　像地球上飛機與塔台間的通信，手機移動信號等都會造成干擾，這樣火星探測器發出的信號等傳到地球早就變了樣。

　　地球這邊的接收方其實一直是靠猜去試圖理解火星上傳回的信息，這樣問題就轉化成了“發送方以什麼形式編碼信息，能讓接收方更容易猜？”。

　　數學家們想到的一種辦法，是把信息打包成“球形編碼”，可以理解成把信息放在像經緯度一樣的座標點上。

　　關鍵在於只使用有限數量的點，只要不同點之間的距離足夠遠又有規律，接收一方就不容易把兩個點的內容混淆。

　　只不過這裏的球説的不是日常中能見到的三維球體，而是用數學描述的高維幾何球體。

　　找到等角線就可以找出那些用來編碼信息效果最好的點。

　　要理解這個問題，還是先回到簡單的二維平面説起。

　　前面説到，二維平面上的等角線最多有3條，相互之間呈60度夾角。

　　用這3條直線可以構造出一個正六邊形，它的6個頂點就適合用來構造球形編碼（雖然在二維空間還只能叫圓形），相鄰的點之間距離相等，經過噪聲干擾後也不容易被誤判成另一個點。

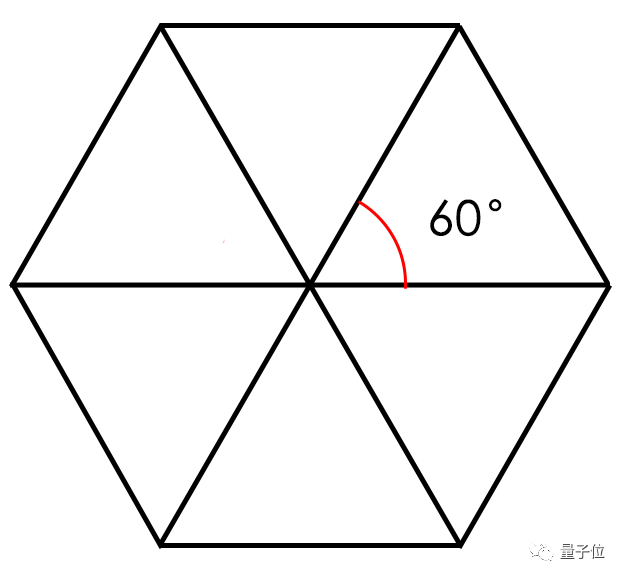
　　之所以要尋找等角線數量的最大值，是因為合適的點越多能發送的信息量也就越多。

　　如果換成三維，就是經過正二十面體中心的6條對角線。

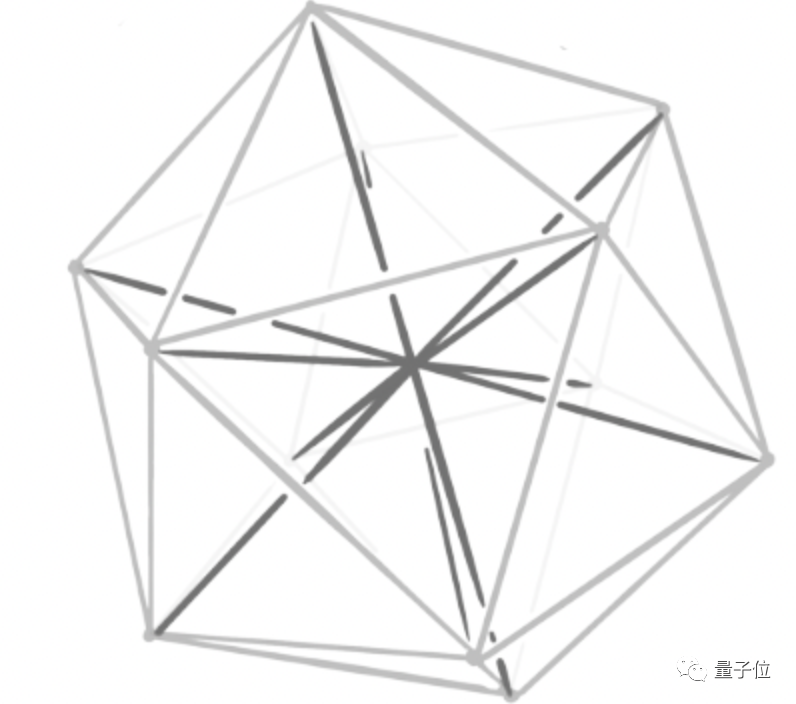
　　不過三維球形編碼能發送的數據量，對於火星與地球間通信來説還是遠遠不夠。

　　如何計算出更高維空間中等角線的最大值，就成了數學家們努力的目標。

　　用矩陣研究高維幾何

　　很長一段時間裏，數學家們能做到的就是證明等角線數量的最大值大致不能超過維度數的平方。

　　更具體一些，設維度數為d，d維空間的等角線數量最大值不能超過下面這個值：

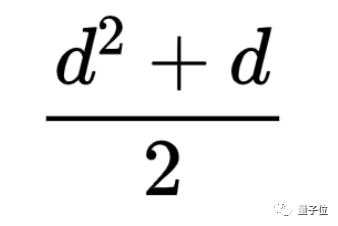
　　直到2017年，蘇黎世聯邦理工學院的Benny Sudakov教授的研究才在這一問題上取得了重要進展。

　　Sudakov的方法是用線性代數和圖論的方法來研究這個問題。

　　還是拿二維平面舉例，先沿着每條線畫一個單位向量：

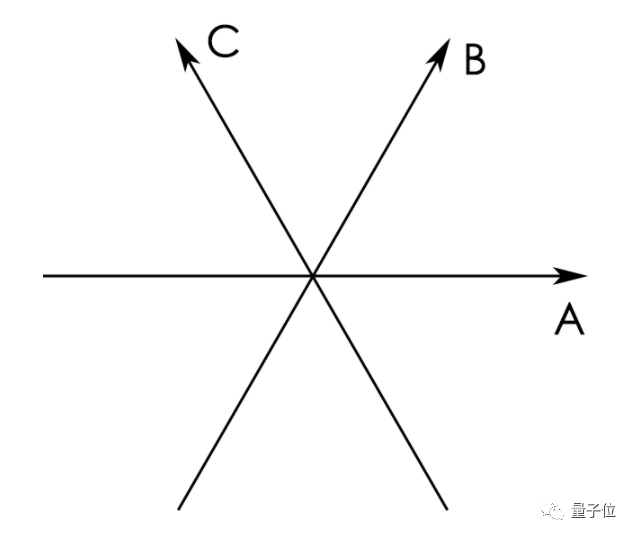
　　再去計算每兩條向量之間的點積：

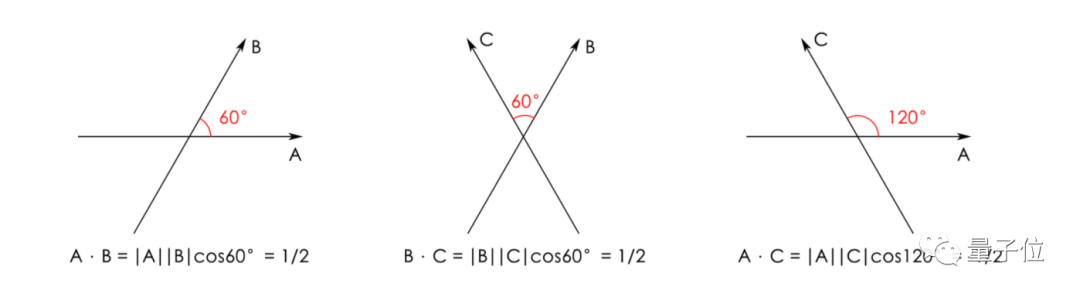
　　接下來需要圖論的方法建立一個圖，向量是圖中的點。如果向量間的點積是正的，邊就是紅色；點積是負的，邊就是藍色。

　　進而可以用矩陣表示這個圖：

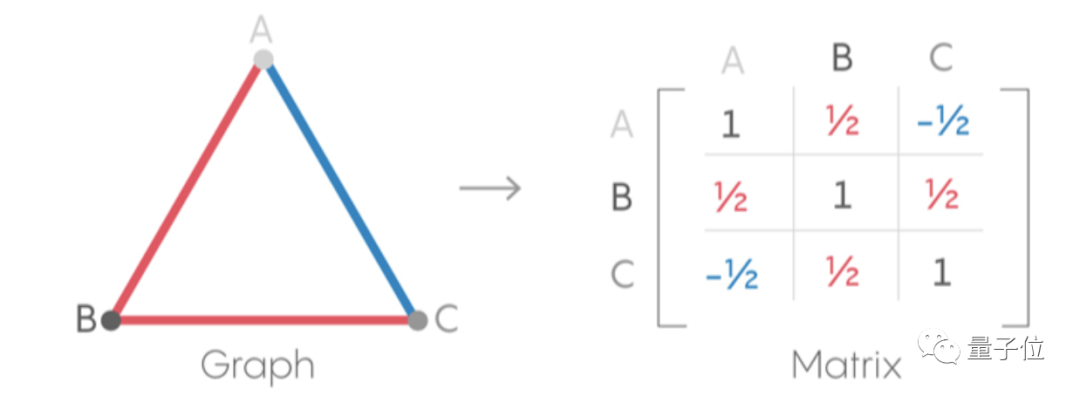
　　****△圖源：Quantum Magzine

　　高維等角線也可以按這個方法轉換成矩陣表示，比如5維空間中的8個等角線：

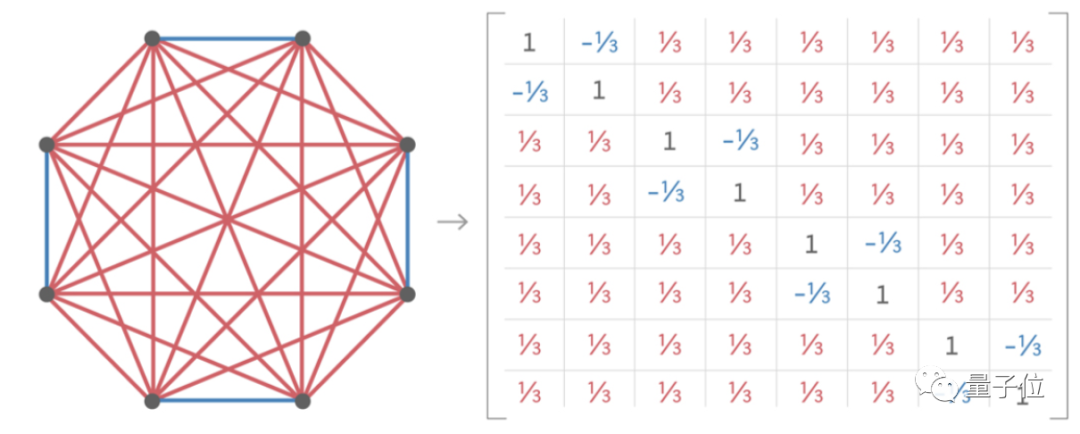
　　****△圖源：Quantum Magzine

　　這樣一個不直觀、不方便研究的高維幾何問題，就可以用上圖論和線性代數里的諸多數學工具。

　　對於這種將高維幾何問題轉換的思路，西門菲沙大學的Jonathan Jedwab形容道：

　　這就像拿光照射3維物體，能看見它在一個方向的2維投影圖；如果在光照下移動3維物體，就能比較不同方向得到的2維投影圖，從而獲得更多高維物體的信息。

　　在對這些矩陣進行研究的過程中，圖論中的拉姆齊定理給了Sudakov靈感。

　　拉姆齊定理認為，找一個最小的自然數R(k,l)=n ，使得n個人中必定有k個人互相認識或l個人互不相識。

　　這裏的k和l，剛好能和矩陣中的正負數對應起來，也就是上面圖中的紅色和藍色。

　　通過將拉姆齊定理的相關結論靈活應用於等角線研究中，Sudakov等人最終證明：

　　對任何d維的圖，在特定角度（約70.7°）下，等角線的最大數目是2d-2；對於其他任何角度，等角線最大數目不超過1.93d。

　　然而，這並不算是一個真正確定的結果，只是再次收緊了“等角線數量”的最大值範圍。

　　現在，來自MIT的趙宇飛團隊，利用一個發現的新定理，給出了這個難題的確定公式。

　　新定理解決70年難題

　　趙宇飛團隊先是在對等角線進行研究中，發現並證明了一個新定理。

　　這個定理認為，有界度圖（bounded degree graph）必須具有次線性第二特徵值重數。

　　其中，度指在圖論中，頂點相連接的邊的數目，因此有限圖一定是有界度圖。

　　神奇的是，這個定理之前並沒有人給出過，但發現它也確實需要非常的洞察力。

　　依據發現的新定理，趙宇飛團隊成功解決了這個70年一直懸而未解的問題：

　　在給定角度的情況下，所有足夠大的任意維度空間中，等角線數量的最大值是多少。

　　具體來説，這篇論文的結論如下：

　　給定數值α滿足0＜α＜1，計算出給定角度arccos α，設d維圖中等角線數量的最大值為。

　　設k代表鄰接矩陣譜半徑為(1 − α)/(2α)的圖的最小頂點數。

　　如果k＜∞，那麼對於所有足夠大的d，都有：

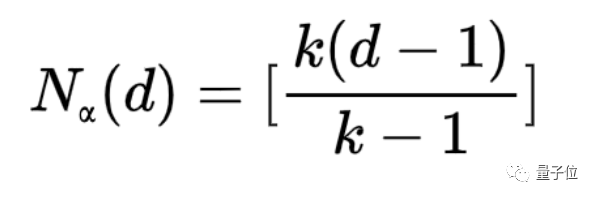
　　否則有：

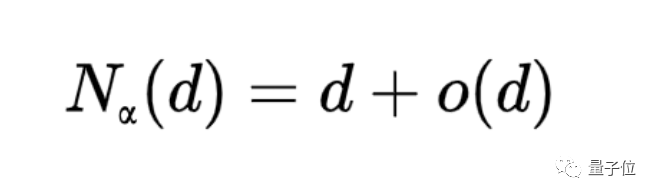
　　特殊地，在k(k為整數)≥2的情況下，對於所有足夠大的d，有：

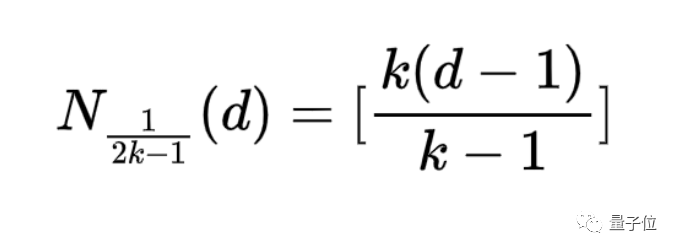
　　在此之前，數學家們的研究一直都停留在研究最大值的範圍上，沒有人能給出在指定角度下，任意維度的等角線數量最大值的確定公式。

　　對於這項研究，趙宇飛表示：

　　當時我有預感，團隊會在等角線上取得一些不錯的進展，但完全解決整個問題還是超出了我的預期。

　　本來是學生暑期項目，最小作者00後

　　這次論文背後的團隊導師趙宇飛（Yufei Zhao），在武漢出生，1999年隨父母移民加拿大。

　　據中新網報道，趙宇飛在中學時被選入資優班，他的數學老師表示“15年間，從未給過學生滿分，直至遇到他”。

　　目前，趙宇飛在MIT任助理教授。

　　他在MIT獲得數學和計算機科學雙學士學位後，於劍橋大學取得碩士學位，並於2015年獲MIT博士學位。

　　在求學期間，趙宇飛深入研究了大圖（足夠大的圖graph）的規律，尤其是對其中的“圖正則引理”進行了深入研究。

　　他認為，在圖數據越來越龐大的當下，大圖的世界是無限的，而圖正則原理、圖極限等數學方法，正是解決圖數據問題的重要工具。

　　也正是基於這一領域的研究成果，趙宇飛獲得了有“諾獎風向標”之稱的斯隆獎、柯尼希獎（König Prize ）和MIT未來科學家獎。

　　雖然他的主要研究領域是加性組合，不過他興趣廣泛，對極值問題和概率論，以及理論計算機科學中的很多問題都感興趣。

　　值得注意的是，趙宇飛的學生Ashwin Sah在本科期間，還曾經對本次研究用到的拉姆齊數理論做出過重要突破。

　　這次與等角線最大值問題結緣，是從2018年先在這一問題作出突破的Sudakov教授到MIT訪問交流開始。

　　趙宇飛是那次交流活動的主持人。

　　Sudakov研究這一問題是受卡耐基梅隆大學的一位學者Bukh Boris啓發，而本次研究的另一位作者博士後姜子麟在博士時的導師正是Boris。

　　到了2019年暑期，趙宇飛和姜子麟帶着共同的興趣將這一課題作為MIT數學系暑期研究項目開展。

　　學生中的3人張盛桐、姚遠和Jonathan Tidor參與了這個項目，5人組成了研究小組。

　　一開始他們只是覺得這個問題足夠大，是一個暑期研究的好項目，也沒想着能取得多大進展。

　　沒想到，最後直接一舉解決了。

　　合影裏中間一位是趙宇飛。

　　左數第一位姜子麟，北大數院校友，CMU博士，以色列理工學院博士後，發表這篇論文期間，他曾經在MIT進行博士後工作。

　　2017年，他曾經與MIPT的Alexandr Polyanskii證明了離散幾何中的一個重要猜想“球帶猜想”（Zone Conjecture），解決了困擾數學家們長達四十餘年的問題。

　　左數第二位是Jonathan Tidor，現MIT博士生，主要研究方向是加性組合、高階傅里葉分析和離散幾何。

　　右數第二位姚遠，上外附中校友，目前是MIT研究生，2016年美國隊IMO金牌滿分選手，連續兩屆獲得阿里全球數學競賽優秀獎和銅獎，普特南大學生數學競賽特等獎（fellow）。

　　右數第一位張盛桐，上海中學校友，MIT本科生（2000年出生），連續三屆獲得阿里全球數學競賽銀獎、2016年國家隊IMO金牌，有“加強版IMO”之稱的普特南大學生數學競賽特等獎（fellow）。

　　據趙宇飛教授2019年的博客，發表這篇文章時，姚遠和張盛桐分別都還是MIT的本科生，其中姚遠就讀大二，張盛桐則剛上大一：

　　本科生階段的研究成果就登上四大頂刊之一《數學年刊》，也是很厲害了。

　　ArXiv論文地址：

　　https://arxiv.org/abs/1907.12466

　　參考鏈接：

　　[1]https://annals.math.princeton.edu/articles/18190

　　[2]https://math.mit.edu/directory/profile.php?pid=1354

　　[3]https://news.mit.edu/2021/mathematicians-solve-old-geometry-problem-equiangular-lines-1004

　　[4]https://www.quantamagazine.org/a-new-path-to-equal-angle-lines-20170411/

　　[5]https://www.quantamagazine.org/how-spherical-codes-work-20170412/

　　[6]https://www.zilin.one/

　　[7]https://www.quantamagazine.org/how-spherical-codes-work-20170412/

　　[8]https://www.linkedin.com/in/shengtong-zhang-73a642197/

　　[9]https://math.mit.edu/directory/profile?pid=2324

　　[10]https://yufeizhao.com/blog/2019/07/30/equiangular-lines-with-a-fixed-angle/

　　[11]https://news.mit.edu/2019/mit-students-place-highly-putnam-mathematical-competition-0304

　　[12]http://www.chinanews.com/hr/mzhrxw/news/2006/07-24/762695.shtml