天機運化,人道可窺;數度相推,算必程式_風聞
文渊紫光-2021-10-22 00:21
總論
天機運化,人道可窺;數度相推,算必程式。
然而謬言數有神理者,在中為推衍預言,在西為名稱義理循辨。
《海島算經》由劉徽於三國魏景元四年(公元263年)撰成,本為《九章算術注》之第十卷,題為《重差》。
唐初開始單行,體例亦是應用型的問題集形式。研究的對象全是有關高度與距離的測量。
所使用的工具也都是利用垂直關係所連接起來的測竿與橫棒。
有人説是實用三角法的啓蒙,不過其內容並未涉及三角學中的正餘弦概念。
所有問題都是利用兩次或多次測望所得的數據,來推算可望而不可及的目標的高、深、廣、遠。
此卷書被收錄入明成祖時編修的永樂大典中,現保存在英國劍橋大學圖書館。
《海島算經》共設九問,均是利用表尺從不同位置多次測望,取多次測量所得的差數,進行計算從而求得山高或谷深,這就是劉徽的重差理論。
《海島算經》中,從題目文字可知所有計算都是用籌算進行的。“為實”指作為一個分數的分子,“為法”指作為分數的分母。所用的長度單位有裏、丈、步、尺、寸:1裏=180丈=1800尺;1丈=10尺:1步=6尺,1尺=10寸。
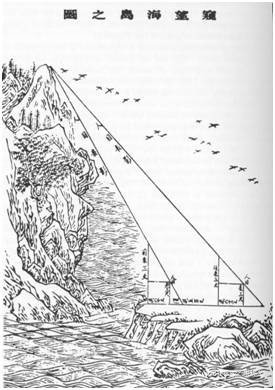
第一題:
今有望海島,立兩表,齊高三丈,前後相去千步,令後表與前表參相直。從前表卻行一百二十三步,人目着地取望島峯,與表末參合。從後表卻行一百二十七步,人目着地取望島峯,亦與表末參合。問島高及去表各幾何?
答曰:島高四里五十五步;去表一百二里一百五十步。
術曰:以表高乘表間為實;相多為法,除之。所得加表高,即得島高。求前表去島遠近者:以前表卻行乘表間為實;相多為法。除之,得島去表數。
今人解答:
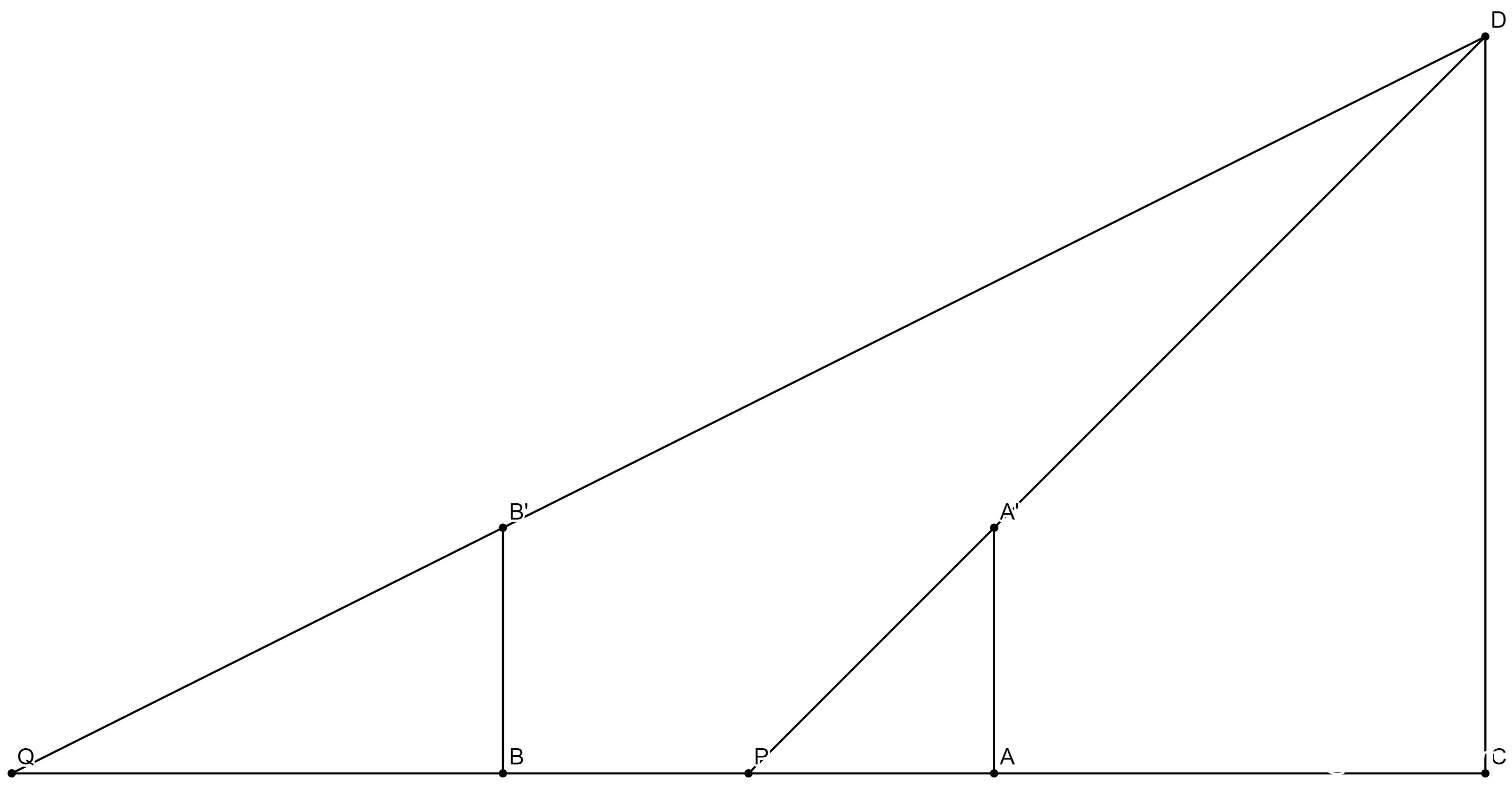
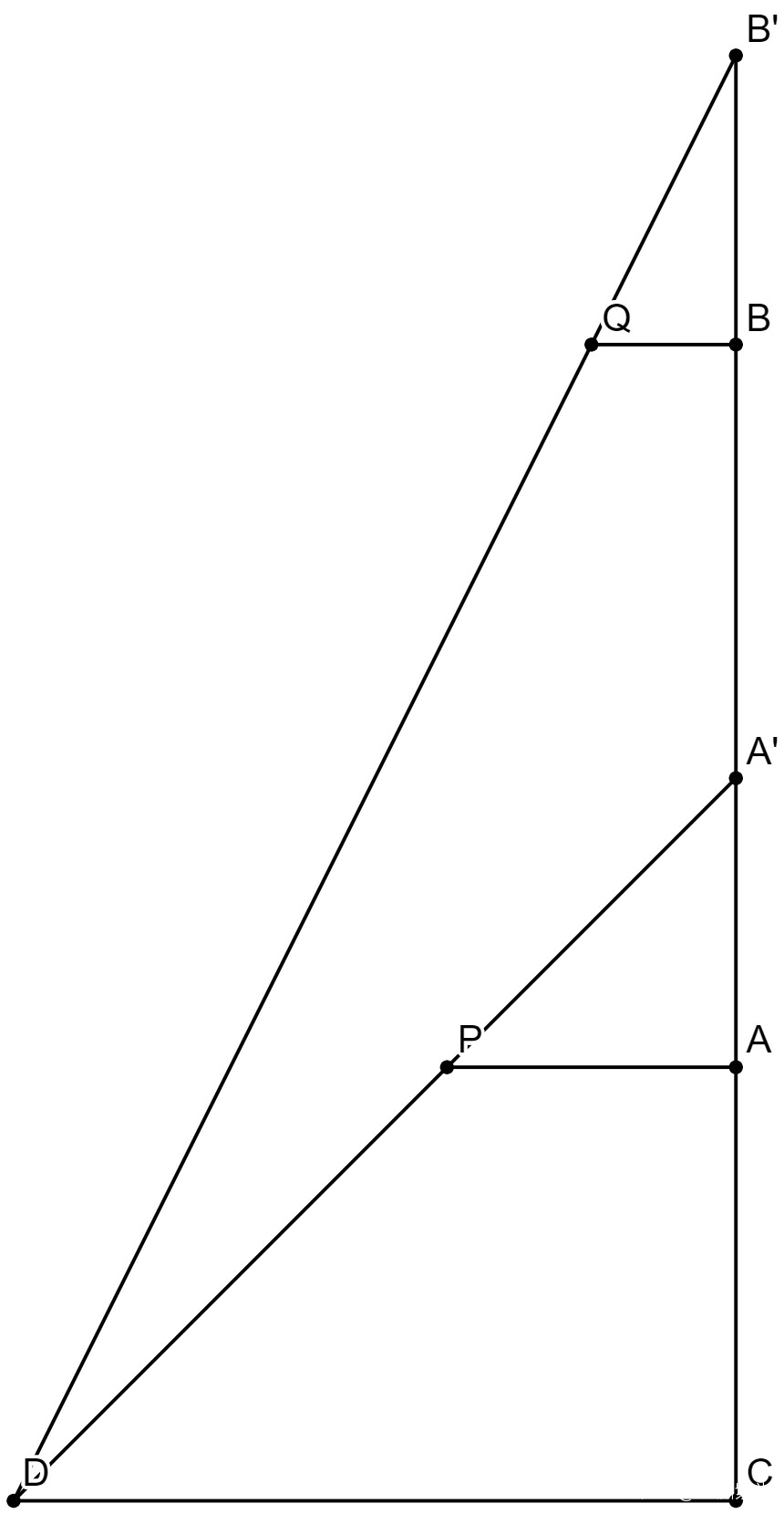
AA’和BB’是兩根標杆(兩表),現在的目標是測量CD的高度(島高)和CA的距離(去表)。
已知從P點通過A’剛好望到D,從Q點通過B’也剛好望到D。則根據相似三角形屬性:
CD/CP = AA’/AP
CD/CQ = BB’/BQ
∵AA’=BB’ → CP/AP = CD/AA’ = CD/BB’ = CQ/BQ
(CA+AP)/AP = (CA+AB+BQ)/BQ
CA/AP = (CA+AB)/BQ
CA*BQ = (CA+AB)*AP = CA*AP + AB*AP
CA*(BQ-AP) = AB*AP
CA = AB*AP/(BQ-AP)
CD = CP*AA’/AP = (CA+AP)*AA’/AP = CA*AA’/AP + AA’ = AB*AA’/(BQ-AP) + AA'
【術曰:以表高乘表間為實;相多為法,除之。所得加表高,即得島高。求前表去島遠近者:以前表卻行乘表間為實;相多為法。除之,得島去表數。】這裏【表高】=AA’,【表間】=AB,【相多】=BQ-AP,【前表卻行】=AP,跟以上兩道等式完全吻合!
【今有望海島,立兩表,齊高三丈,前後相去千步,令後表與前表參相直。從前表卻行一百二十三步,人目着地取望島峯,與表末參合。從後表卻行一百二十七步,人目着地取望島峯,亦與表末參合。問島高及去表各幾何?】
這裏以步作基本單位:
【表高】=3丈=30尺=5步(AA’=5),
【表間】=1000步(AB=1000),
【前表卻行】=123步(AP=123),
【後表卻行】=127步(BQ=127),
【相多】=127-123=4步(BQ-AP=4)。
得:CD = AB*AA’/(BQ-AP) + AA’ = 1000*5/4 + 5 = 1250 + 5 = 1255CA = AB*AP/(BQ-AP) = 1000*123/4 = 30750
【答曰:島高四里五十五步;去表一百二里一百五十步。】【島高】= 4裏 + 55步 = 7200尺 + 55步 = 1200步 + 55步 = 1255步【去表】= 102裏 + 150步 = 183600尺 + 150步 = 30600步 + 150步 = 30750步,結果完全吻合!
第二題
今有望松生山上,不知高下。立兩表齊,高二丈,前後相去五十步,令後表與前表參相直。從前表卻行七步四尺,薄地遙望松末,與表端參合。又望松本,入表二尺八寸。復從後表卻行八步五尺,薄地遙望松末,亦與表端參合。問松高及山去表各幾何?
答曰:松高一十二丈二尺八寸;山去表一里二十八步、七分步之四。
術曰:以入表乘表間為實。相多為法,除之。加入表,即得松高。求表去山遠近者:置表間,以前表卻行乘之為實。相多為法,除之,得山去表。
今人解答:
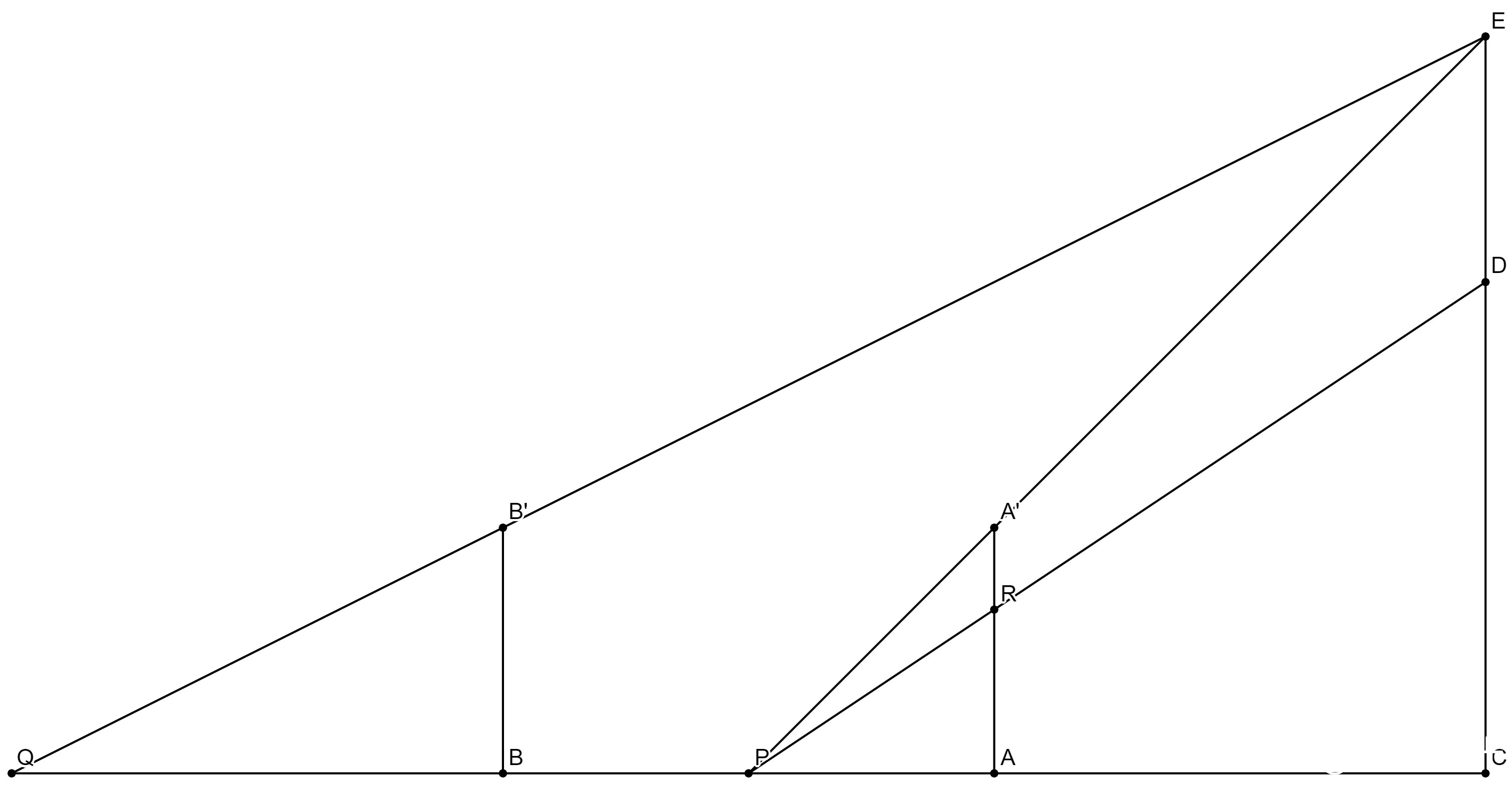
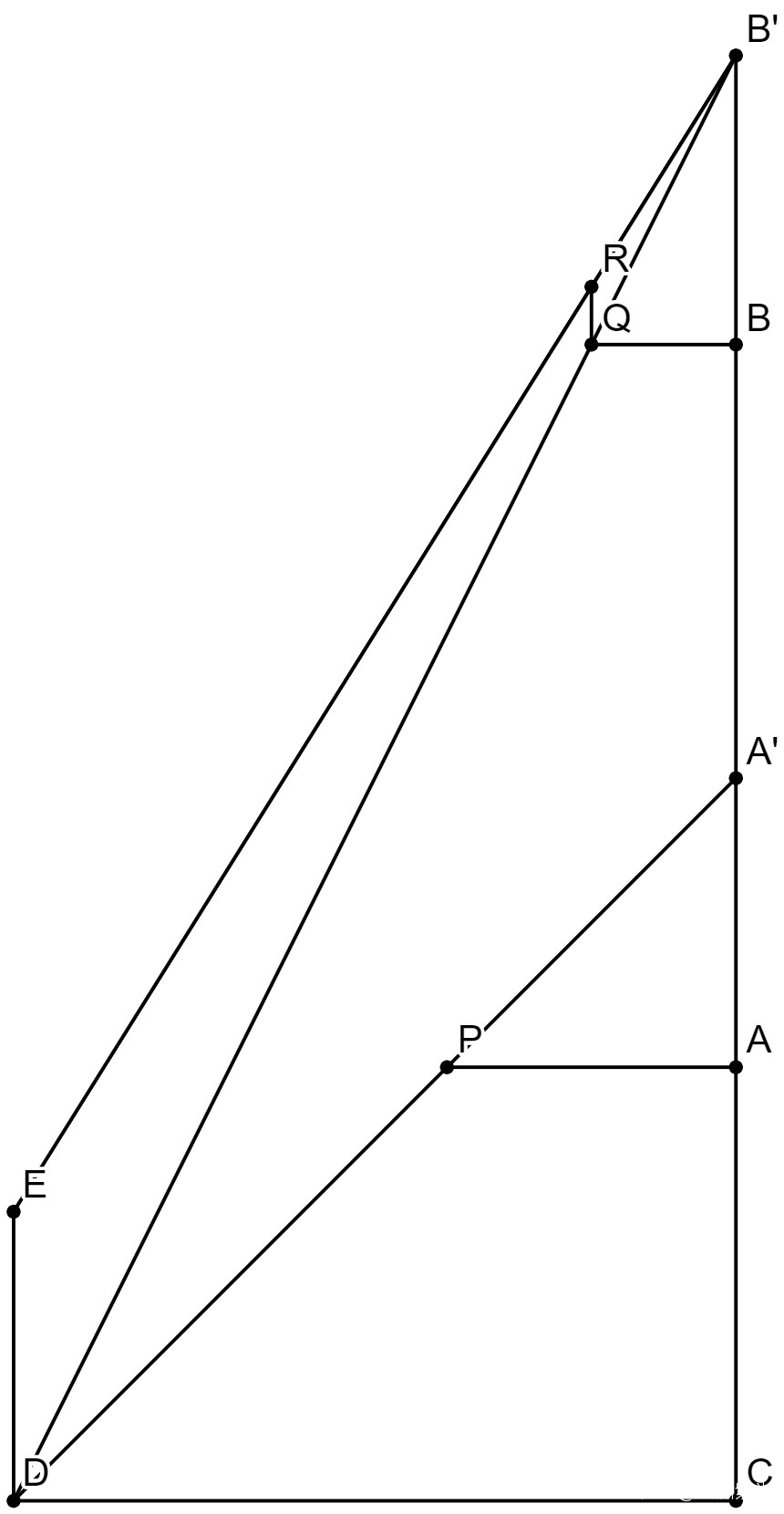
AA’和BB’是兩根標杆(兩表),
R是AA’上的一個刻度點,
現在的目標是測量DE的高度(松高)和CA的距離(山去表)。
已知從P點通過A’剛好望到E,通過R剛好望到D,又從Q點通過B’也剛好望到E。
則根據相似三角形屬性:
CE/CP=AA’/AP
CE/CQ=BB’/BQ
CD/CP=AR/AP
∵AA’=BB’ → CP/AP = CE/AA’ = CE/BB’ = CQ/BQ
(CA+AP)/AP = (CA+AB+BQ)/BQ
CA/AP = (CA+AB)/BQ
CA*BQ = (CA+AB)*AP = CA*AP + AB*AP
CA*(BQ-AP) = AB*AP
CA = AB*AP/(BQ-AP)
DE = CE - CD = CP*AA’/AP - CP*AR/AP = (CA+AP)*(AA’-AR)/AP
DE = AB*RA’/(BQ-AP) + RA'
【術曰:以入表乘表間為實。相多為法,除之。加入表,即得松高。求表去山遠近者:置表間,以前表卻行乘之為實。相多為法,除之,得山去表。】
這裏【入表】=RA’,【表間】=AB,【相多】=BQ-AP,【前表卻行】=AP,式子完全吻合!
【今有望松生山上,不知高下。立兩表齊,高二丈,前後相去五十步,令後表與前表參相直。從前表卻行七步四尺,薄地遙望松末,與表端參合。又望松本,入表二尺八寸。復從後表卻行八步五尺,薄地遙望松末,亦與表端參合。問松高及山去表各幾何?】
這次以【尺】為基本單位:
【表高】=2丈=20尺(AA’=20),
【表間】=50步=300尺(AB=300),
【前表卻行】=7步+4尺=46尺(AP=46),
【後表卻行】=8步+5尺=53尺(BQ=53),
【相多】=53-46=7尺(BQ-AP=7),
【入表】=2尺+8寸=2.8尺(RA’=2.8)。
得:DE = AB*RA’/(BQ-AP) + RA’ = 300*2.8/7 + 2.8 = 122.8CA = AB*AP/(BQ-AP) = 300*46/7 = 1971+3/7
【答曰:松高一十二丈二尺八寸;山去表一里二十八步、七分步之四。】
【松高】= 12丈 + 2尺 + 8寸 = 120尺 + 2.8尺 = 122.8尺
【山去表】= 1裏 + 28步 + 4/7步 = 1800尺+ 168尺 + 24/7尺 = 1971+3/7尺結果完全吻合!
第三題:
今有南望方邑,不知大小。立兩表東、西去六丈,齊人目,以索連之。令東表與邑 東南隅及東北隅參相直。當東表之北卻行五步,遙望邑西北隅,入索東端二丈二尺六寸半。又卻北行去表一十三步二尺,遙望邑西北隅,適與西表相參合。問邑方及邑去表各幾何?
答曰:邑方三里四十三步、四分步之三;邑去表四里四十五步。
術曰:以入索乘後去表,以兩表相去除之,所得為景長;以前去表減之,不盡以為法。置後去表,以前去表減之,餘以乘入索為實。實如法而一,得邑方。求去表遠近者:置後去表,以景長減之,餘以乘前去表為實。實如法而一,得邑去表。
今人解答:
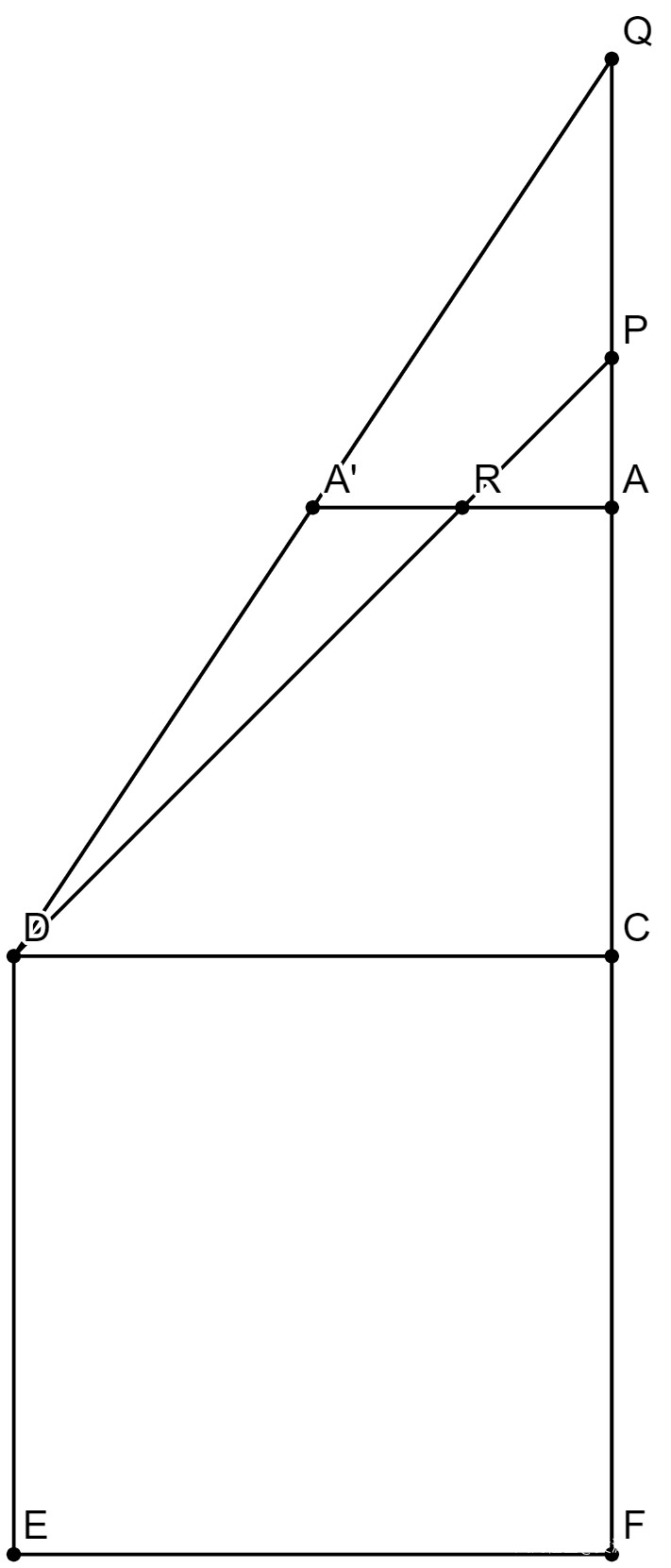
CDEF是一個四牆分別面向正東南西北方的正方形邑城,
A和A’分別是兩根標杆,
中間用一條繩索AA’連着,
R是AA’上的一個刻度點,
現在的目標是測量CD的寬度(邑方)和CA的距離(邑去表)。
已知FCAPQ成一直線,
AA’與CD平行,
從P點通過R剛好望向D,從Q點通過A’也剛好望向D。
則根據相似三角形屬性:
CD/CP = AR/AP
CD/CQ = AA’/AQ
CP*AR/AP = CD = CQ*AA’/AQ
(CA+AP)*AQ*AR = (CA+AQ)*AP*AA'
CA*AQ*AR + AP*AQ*AR = CA*AP*AA’ + AQ*AP*AA'
CA*AQ*AR - CA*AP*AA’ = AP*AQ*AA’ - AP*AQ*AR
CA*AQ*AR/AA’ - CA*AP = AP*AQ - AP*AQ*AR/AA'
CA*(AQ*AR/AA’-AP) = AP*(AQ-AQ*AR/AA')
CA = (AQ-AQ*AR/AA’)*AP / (AQ*AR/AA’-AP)
CD = CQ*AA’/AQ = (CA+AQ)*AA’/AQ = CA*AA’/AQ + AA'
CD = (AA’-AR)*AP/(AQ*AR/AA’-AP) + (AQ*AR-AP*AA’)/(AQ*AR/AA’-AP)
CD = (AQ-AP)*AR / (AQ*AR/AA’-AP)
【術曰:以入索乘後去表,以兩表相去除之,所得為景長;以前去表減之,不盡以為法。置後去表,以前去表減之,餘以乘入索為實。實如法而一,得邑方。求去表遠近者:置後去表,以景長減之,餘以乘前去表為實。實如法而一,得邑去表。】
【入索】=AR,
【後去表】=AQ,
【兩表相去】=AA’,
【景長】=AQ*AR/AA’,
【前去表】=AP,
【不盡】=AQ*AR/AA’-AP,
式子完全吻合!
【今有南望方邑,不知大小。立兩表東、西去六丈,齊人目,以索連之。令東表與邑東南隅及東北隅參相直。當東表之北卻行五步,遙望邑西北隅,入索東端二丈二尺六寸半。又卻北行去表一十三步二尺,遙望邑西北隅,適與西表相參合。問邑方及邑去表各幾何?】
【兩表相去】=AA’=6丈=60尺,
【前去表】=AP=5步=30尺,
【入索】=AR=2丈+2尺+6.5寸=22.65尺,
【後去表】=AQ=13步+2尺=80尺,
【景長】=80*22.65/60=30.2尺,
【不盡】=30.2-30=0.2尺。
得:CD = (AQ-AP)*AR / (AQ*AR/AA’-AP) = (80-30)*22.65 / 0.2 = 5662.5CA = (AQ-AQ*AR/AA’)*AP / (AQ*AR/AA’-AP) = (80-30.2)*30 / 0.2 = 7470
【答曰:邑方三里四十三步、四分步之三;邑去表四里四十五步。】
【邑方】= 3裏 + 43步 + 3/4步 = 5400尺 + 258尺 + 18/4尺 = 5662.5尺
【邑去表】= 4裏 + 45步 = 7200尺 + 270尺 = 7470尺
結果完全吻合!
第四題:
今有望深谷,偃矩岸上,令勾高六尺。從勺端望谷底,入下股九尺一寸。又設重矩於上,其矩間相去三丈。更從勺端望谷底,入上股八尺五寸。問谷深幾何?
答曰:四十一丈九尺。
術曰:置矩間,以上股乘之,為實。上、下股相減,餘為法,除之。所得以勾高減之,即得谷深。
今人解答:
AA’和BB’是在深谷懸崖邊上豎起的兩段垂直柱子(勾),
AP和BQ則為柱子底部伸出的水平杆子(股),
P、Q為杆子上面的刻度點,
CD為深谷底部的一條水平線,
現在的目標是測量CA的長度(谷深)。
已知從A’通過P點剛好望到D,
從B’通過Q點也剛好望到D。
則根據相似三角形屬性:
CD/CA’ = AP/AA'
CD/CB’ = BQ/BB'
∵AA’ = BB’ → CA’*AP = CD*AA’ = CD*BB’ = CB’*BQ
(CA+AA’)*AP = (CA+AB+BB’)*BQ
CA*AP-CA*BQ = AB*BQ+BB’*BQ-AA’*AP
CA*(AP-BQ) = AB*BQ-AA’*(AP-BQ)
CA = AB*BQ/(AP-BQ)-AA'
【術曰:置矩間,以上股乘之,為實。上、下股相減,餘為法,除之。所得以勾高減之,即得谷深。】
【矩間】=AB,
【上股】=BQ,
【下股】=AP,
【勾高】=AA’,
式子完全吻合!
【今有望深谷,偃矩岸上,令勾高六尺。從勺端望谷底,入下股九尺一寸。又設重矩於上,其矩間相去三丈。更從勺端望谷底,入上股八尺五寸。問谷深幾何?】
【勾高】=AA’=6尺,
【下股】=AP=9尺+1寸=9.1尺,
【矩間】=AB=3丈=30尺,
【上股】=BQ=8尺+5寸=8.5尺。
得:CA = AB*BQ/(AP-BQ)-AA’ = 30*8.5/(9.1-8.5)-6 = 419
【答曰:四十一丈九尺。】
【谷深】= 41丈+9尺 = 419尺結果完全吻合!
第五題:
今有登山望樓,樓在平地。偃矩山上,令勾高六尺。從勾端斜望樓足,入下股一丈二尺。又設重矩於上,令其間相去三丈。更從勾端斜望樓足,入上股一丈一尺四寸。又立小表於入股之會,復從勾端斜望樓岑端,入小表八寸。問樓高几何?
答曰:八丈。
術曰:上、下股相減,餘為法;置矩間,以下股乘之,如勾高而一。所得,以入小表乘之,為實。實如法而,即是樓高。
今人解答:
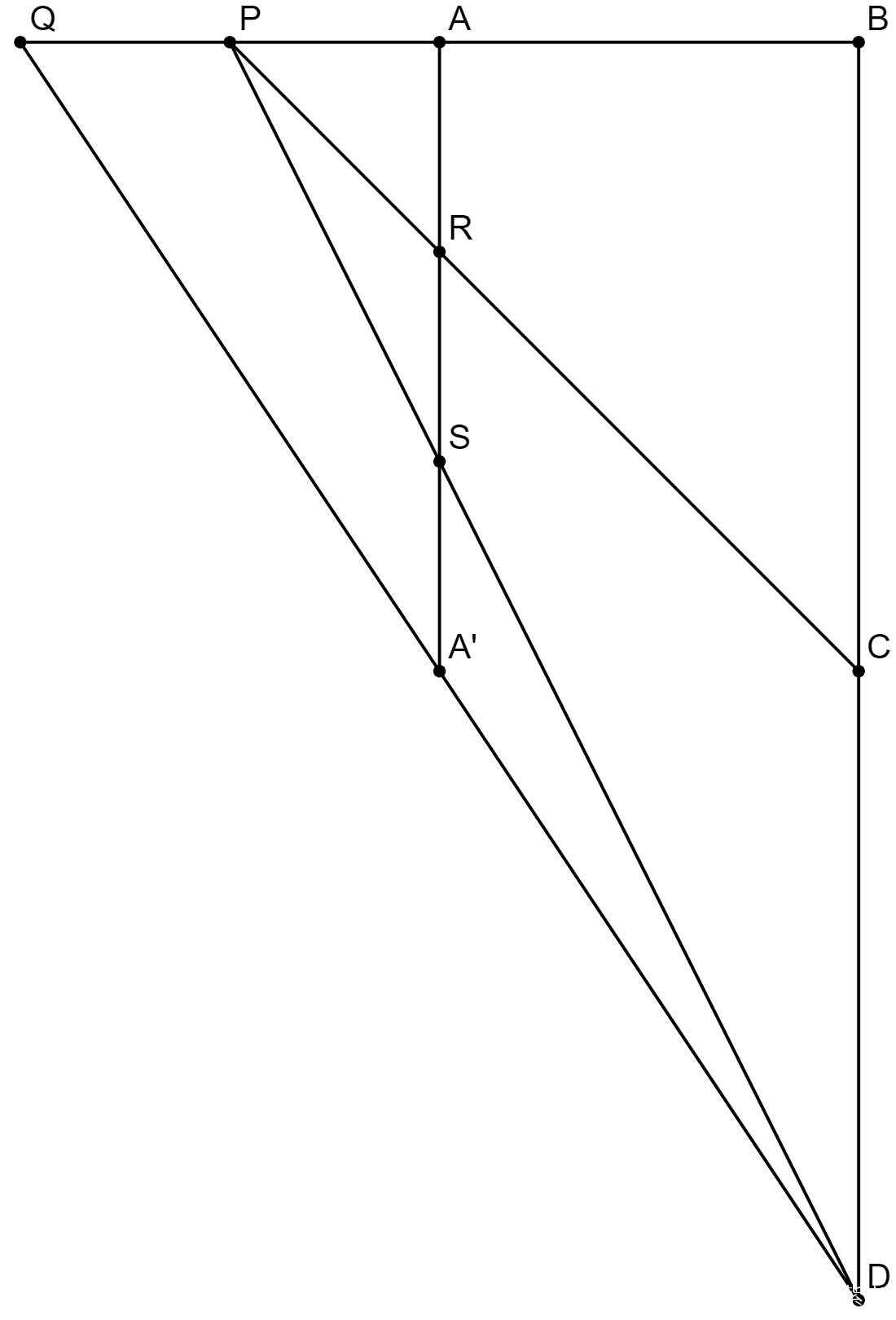
AA’和BB’是在山上豎起的兩段垂直柱子(勾),
AP和BQ則為柱子底部伸出的水平杆子(股),
P、Q為杆子上面的刻度點。
另外在Q點上豎立起一根小標杆QR,
R為上面的一個刻度點。
DE為山下平地上的一座高樓,
現在的目標是測量它的高度(樓高)。
已知從A’通過P點剛好望到D,
從B’通過Q點也剛好望到D,
通過R點則剛好望到E。
則根據相似三角形屬性:
CD/CA’ = AP/AA'
CD/CB’ = BQ/BB'
CD/(CB’-DE) = BQ/(BB’-QR)
∴BQ*CB’/BB’*(BB’-QR) = BQ*(CB’-DE)
CB’-DE = CB’-CB’*QR/BB'
DE = (CA+AB+BB’)*QR/BB'
從上題得:
CA = AB*BQ/(AP-BQ)-AA'
又:AA’ = BB'
∴DE = (AB*BQ/(AP-BQ)+AB)*QR/AA’DE = AB*AP/AA’*QR/(AP-BQ)
【術曰:上、下股相減,餘為法;置矩間,以下股乘之,如勾高而一。所得,以入小表乘之,為實。實如法而,即是樓高。】
【上股】=BQ,
【下股】=AP,
【矩間】=AB,
【勾高】=AA’,
【入小表】=QR,
式子完全吻合!
【今有登山望樓,樓在平地。偃矩山上,令勾高六尺。從勾端斜望樓足,入下股一丈二尺。又設重矩於上,令其間相去三丈。更從勾端斜望樓足,入上股一丈一尺四寸。又立小表於入股之會,復從勾端斜望樓岑端,入小表八寸。問樓高几何?】
【勾高】=AA’=6尺,
【下股】=AP=1丈+2尺=12尺,
【矩間】=AB=3丈=30尺,
【上股】=BQ=1丈+1尺+4寸=11.4尺,
【入小表】=QR=8寸=0.8尺。
得:DE = AB*AP/AA’*QR/(AP-BQ) = 30*12/6*0.8/(12-11.4) = 80
【答曰:八丈。】
【樓高】= 8丈 = 80尺
結果完全吻合!
第六題:
今有東南望波口,立兩表南、北相去九丈,以索薄地連之。當北表之西卻行去表六丈,薄地遙望波口南岸,入索北端四丈二寸。以望北岸,入前所望表裏一丈二尺。又卻行,後去表一十三丈五尺。薄地遙望波口南岸,與南表參合。問波口廣幾何?
答曰:一里二百步。
術曰:以後去表乘入索,如表相去而一。所得,以前去表減之,餘以為法;復以前去表減後去表,餘以乘入所望表裏為實,實如法而一,得波口廣。
今人解答:
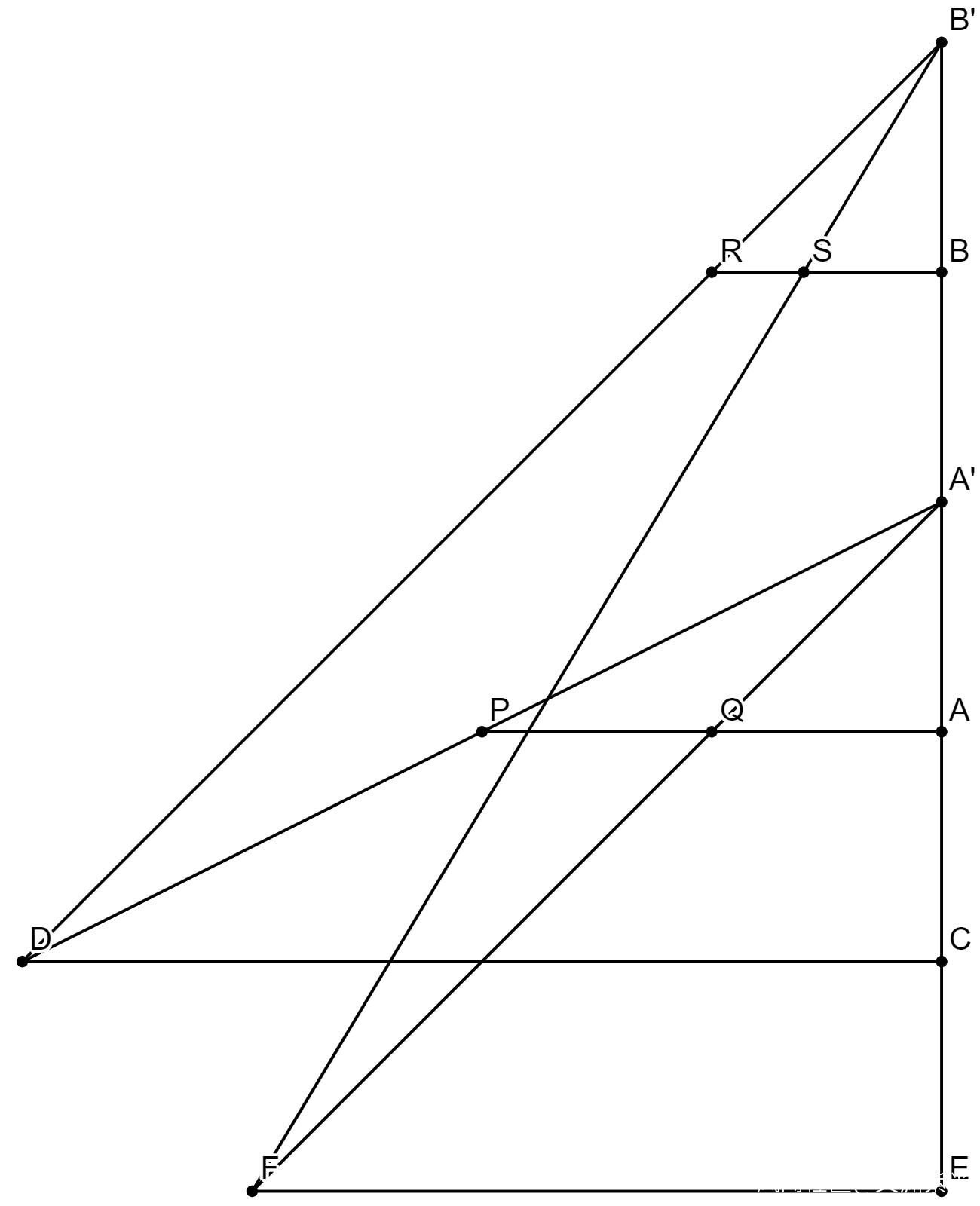
CD是一個縱貫南北的波口(河口),
A和A’分別是兩根標杆,
中間用一條繩索AA’連着,
R和S是AA’上的兩個刻度點,
現在的目標是測量CD的寬度(波口廣)。
已知AA’與CD平行,
APQ與CD垂直,
B點為APQ與CD的延長線交點,
從P點通過R剛好望向C,
通過S則剛好望向D,
從Q點通過A’也剛好望向D。
則根據相似三角形屬性:
BC/BP = AR/AP
BD/BP = AS/AP
→(BC+CD)/BP = (AR+RS)/AP
→BP = CD*AP/RS
BD/BQ = AA’/AQ
→BD*AQ = (BP+PQ)*AA'
→(BP*AS/AP)*AQ = BP*AA’+PQ*AA'
→(CD*AP/RS)*(AQ*AS/AP-AA’) = (AQ-AP)*AA'
→CD*(AQ*AS-AP*AA’)/RS = (AQ-AP)*AA'
CD = (AQ-AP)*RS/(AQ*AS/AA’-AP)
【術曰:以後去表乘入索,如表相去而一。所得,以前去表減之,餘以為法;復以前去表減後去表,餘以乘入所望表裏為實,實如法而一,得波口廣。】
【後去表】=AQ,
【入索】=AS,
【表相去】=AA’,
【前去表】=AP,
【入所望表裏】=RS,
式子完全吻合!
【今有東南望波口,立兩表南、北相去九丈,以索薄地連之。當北表之西卻行去表六丈,薄地遙望波口南岸,入索北端四丈二寸。以望北岸,入前所望表裏一丈二尺。又卻行,後去表一十三丈五尺。薄地遙望波口南岸,與南表參合。問波口廣幾何?】
【表相去】=AA’=9丈=90尺,
【前去表】=AP=6丈=60尺,
【入索】=AS=4丈+2寸=40.2尺,
【入所望表裏】=RS=1丈+2尺=12尺,
【後去表】=AQ=13丈+5尺=135尺。
得:CD = (AQ-AP)*RS/(AQ*AS/AA’-AP) = (135-60)*12/(135*40.2/90-60) = 900/0.3 = 3000【答曰:一里二百步。】
【波口廣】= 1裏 + 200步 = 1800尺 + 1200尺 = 3000尺
結果完全吻合!
第七題:
今有望清淵下有白石。偃矩岸上,令勾高三尺。斜望水岸,入下股四尺五寸。望白石,入下股二尺四寸。又設重矩於上,其間相去四尺。更從勾端斜望水岸,入上股四尺。以望白石,入上股二尺二寸。問水深幾何?
答曰:一丈二尺。
術曰:置望水上、下股相減,餘以乘望石上股為上率。又以望石上、下股相減,餘以乘望水上股為下率。兩率相減,餘以乘矩間為實;以二差相乘為法。實如法而一,得水深。
今人解答:
AA’和BB’是在岸上豎起的兩段垂直柱子(勾),
AP和BR則為柱子底部伸出的水平杆子(股),
P、Q、R、S為杆子上面的刻度點,
CD為清淵水面的水平線,
EF為淵底的水平線,F點有顆白石。
現在的目標是測量CE的長度(水深)。
已知從A’通過P點剛好望到D,
通過Q點剛好望到F,
從B’通過R點剛好望到D,
通過S點剛好望到F。
則根據相似三角形屬性:
CD/CA’ = AP/AA'
EF/EA’ = AQ/AA'
CD/CB’ = BR/BB'
EF/EB’ = BS/BB'
∵AA’ = BB’ → CA’*AP = CD*AA’ = CD*BB’ = CB’*BR
(CA+AA’)*AP = (CA+AB+BB’)*BR
CA*AP-CA*BR = AB*BR+AA’*BR-AA’*AP
CA*(AP-BR) = AB*BR-AA’*(AP-BR)
CA = AB*BR/(AP-BR)-AA'
∵AA’ = BB’ → EA’*AQ = EF*AA’ = EF*BB’ = EB’*BS
(EA+AA’)*AQ = (EA+AB+BB’)*BS
EA*AQ-EA*BS = AB*BS+AA’*BS-AA’*AQ
EA*(AQ-BS) = AB*BS-AA’*(AQ-BS)
EA = AB*BS/(AQ-BS)-AA'
∴CE = EA-CA = AB*BS/(AQ-BS)-AB*BR/(AP-BR)
CE = ((AP-BR)*BS-(AQ-BS)*BR)*AB/(AP-BR)/(AQ-BS)
【術曰:置望水上、下股相減,餘以乘望石上股為上率。又以望石上、下股相減,餘以乘望水上股為下率。兩率相減,餘以乘矩間為實;以二差相乘為法。實如法而一,得水深。】
【望水上股】=BR,
【望水下股】=AP,
【望石上股】=BS,
【望石下股】=AQ,
【矩間】=AB,
式子完全吻合!
【今有望清淵下有白石。偃矩岸上,令勾高三尺。斜望水岸,入下股四尺五寸。望白石,入下股二尺四寸。又設重矩於上,其間相去四尺。更從勾端斜望水岸,入上股四尺。以望白石,入上股二尺二寸。問水深幾何?】
【勾高】=AA’=3尺,
【望水下股】=AP=4尺+5寸=4.5尺,
【望石下股】=AQ=2尺+4寸=2.4尺,
【矩間】=AB=4尺,
【望水上股】=BR=4尺,
【望石上股】=BS=2尺+2寸=2.2尺。
得:CE = ((AP-BR)*BS-(AQ-BS)*BR)*AB/(AP-BR)/(AQ-BS) = ((4.5-4)*2.2-(2.4-2.2)*4)*4/(4.5-4)/(2.4-2.2) = (1.1-0.8)*4/0.5/0.2 = 1.2*2*5 = 12
【答曰:一丈二尺。】
【水深】= 1丈 + 2尺 = 12尺結果完全吻合!
第八題:
今有登山望津,津在山南。偃矩山上,令勾高一丈二尺。從勾端斜望津南岸,入下股二丈三尺一寸。又望津北岸,入前望股裏一丈八寸。更登高巖,北卻行二十二步,上登五十一步,偃矩山上。更從勾端斜望津南岸,入上股二丈二尺。問津廣幾何?
答曰:二里一百二步。
術曰:以勾高乘下股,如上股而一。所得以勾高減之,餘為法;置北行,以勾高乘之,如上股而一。所得以減上登,餘以乘入股裏為實。實如法而一,即得津廣。
今人解答:
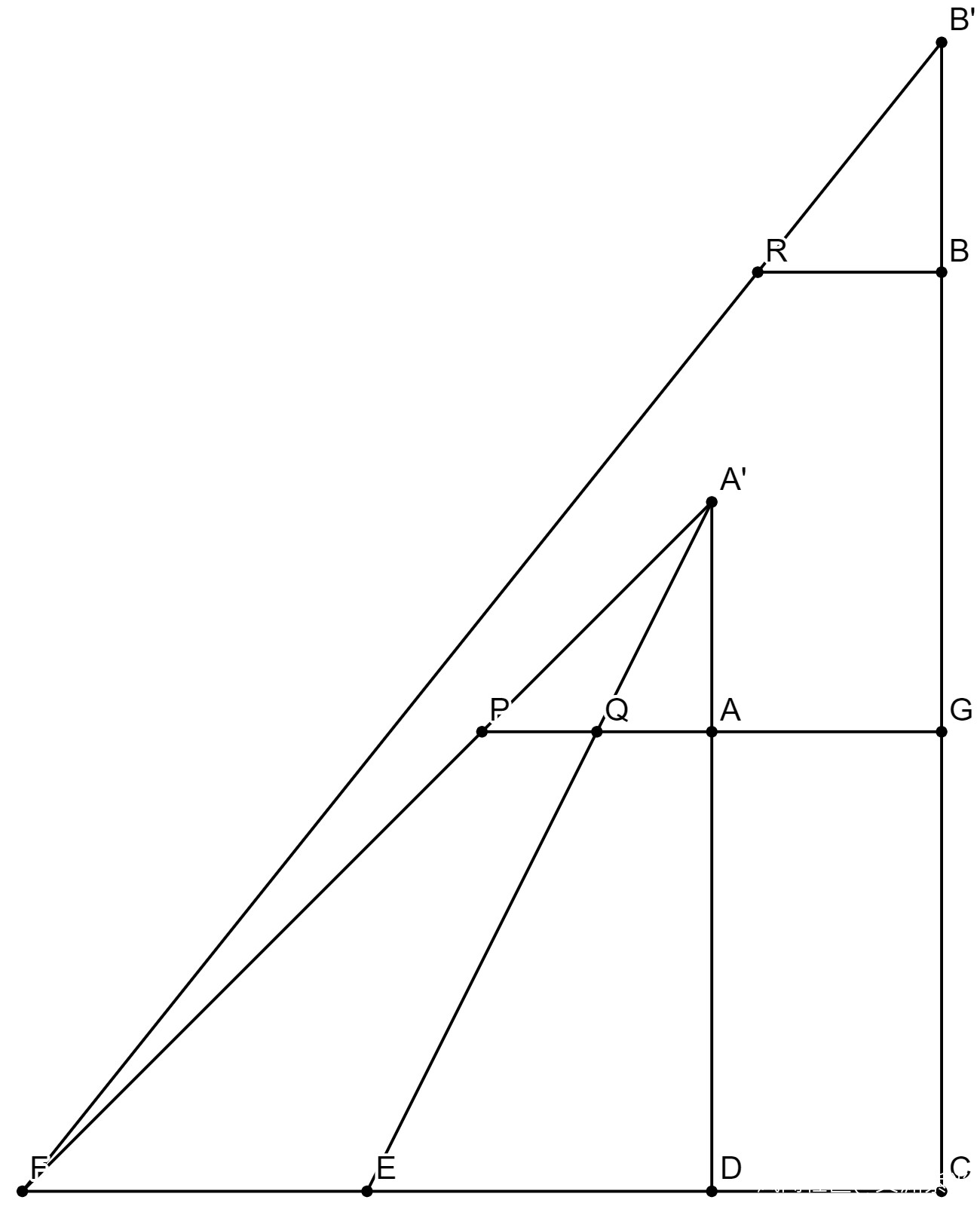
AA’和BB’是在山上兩處豎起的垂直柱子(勾),
AP和BR則為柱子底部伸出的水平杆子(股),
P、Q、R為杆子上面的刻度點,
EF為山下的一個津(渡口)。
現在的目標是測量EF的寬度(津廣)。
已知從A’通過P點剛好望到F,
通過Q點剛好望到E,
從B’通過R點剛好望到F。
則根據相似三角形屬性:
DF/DA’ = AP/AA'
DE/DA’ = AQ/AA'
→EF = DF-DE = DA’*(AP-AQ)/AA’ = DA’*PQ/AA'
CF/CB’ = BR/BB'
→(CD+DF)*BB’ = (CG+GB+BB’)*BR
→(GA+DA’*AP/AA’)*AA’ = (DA+GB+AA’)*BR
→GA*AA’+DA’*AP = DA’*BR+GB*BR
→DA’*(AP-BR) = GB*BR-GA*AA'
→EF*(AP-BR) = (GB*BR-GA*AA’)*PQ/AA'
EF = (GB-GA*AA’/BR)*PQ/(AP*AA’/BR-AA')
【術曰:以勾高乘下股,如上股而一。所得以勾高減之,餘為法;置北行,以勾高乘之,如上股而一。所得以減上登,餘以乘入股裏為實。實如法而一,即得津廣。】
【勾高】=AA’,
【下股】=AP,
【上股】=BR,
【北行】=GA,
【上登】=GB,
【入股裏】=PQ,
式子完全吻合!
【今有登山望津,津在山南。偃矩山上,令勾高一丈二尺。從勾端斜望津南岸,入下股二丈三尺一寸。又望津北岸,入前望股裏一丈八寸。更登高巖,北卻行二十二步,上登五十一步,偃矩山上。更從勾端斜望津南岸,入上股二丈二尺。問津廣幾何?】
【勾高】=AA’=1丈+2尺=12尺,
【下股】=AP=2丈+3尺+1寸=23.1尺,
【入股裏】=PQ=1丈+8寸=10.8尺,
【北行】=GA=22步=132尺,
【上登】=GB=51步=306尺,
【上股】=BR=2丈+2尺=22尺。
得:EF = (GB-GA*AA’/BR)*PQ/(AP*AA’/BR-AA’) = (306-132*12/22)*10.8/(23.1*12/22-12) = 234*10.8/0.6 = 4212【答曰:二里一百二步。】
【津廣】= 2裏 + 102步 = 3600尺 + 612尺 = 4212尺
結果完全吻合!
第九題:
今有登山臨邑,邑在山南。偃矩山上,令勾高三尺五寸。令勾端與邑東南隅及東北隅參相直。從勾端遙望東北隅,入下股一丈二尺。又施橫勾於入股之會,從立勾端望西北隅,入橫勾五尺。望東南隅,入下股一丈八尺。又設重矩於上,令矩間相去四丈。更從立勾端望東南隅,入上股一丈七尺五寸。問邑廣長各幾何?
答曰:南北長一里百步;東西廣一里三十三步、少半步。
術曰:以勾高乘東南隅入下股,如上股而一,所得減勾高,餘為法;以東北隅下股減東南隅下股,餘以乘矩間為實。實如法而一,得邑南北長也。求邑廣:以入橫勾乘矩間為實。實如法而一,即得邑東西廣。
今人解答:
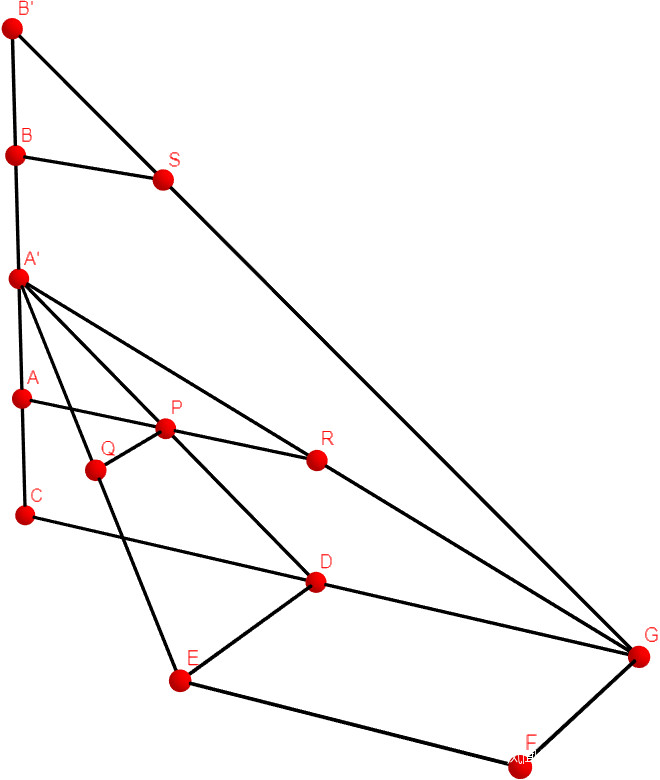
DEFG是一個在地平面上,
四牆分別面向正東南西北方的矩形邑城,
AA’和BB’是在山上豎起的兩段垂直柱子(勾),
AR和BS則為柱子底部伸出的水平杆子(股),
PQ則為從P點向橫伸出跟AR成直角的水平杆子(橫勾),
P、Q、R、S都是杆子上面的刻度點。
現在的目標是測量DG的長度(南北長)和DE的寬度(東西廣)。
已知從A’通過P點剛好望到D,
通過Q點剛好望到E,
通過R點剛好望到G,
從B’通過S點也剛好望到G。
則根據相似三角形屬性:
CD/CA’ = AP/AA'
CG/CA’ = AR/AA'
→CG*AA’ = CA’*AR
CG/CB’ = BS/BB'
→(CA+AB+BB’)*BS = CG*BB'
∴(CA+AB+AA’)*BS = CA’*AR
CA’*(AR-BS) = AB*BS
CA’/AA’ = AB/(AA’*AR/BS-AA')
∴DG = CG-CD = (AR-AP)*CA’/AA'
DG = (AR-AP)*AB/(AA’*AR/BS-AA')
又根據相似三角形屬性:
DA’/CA’ = PA’/AA'
DE/DA’ = PQ/PA'
∴DE = PQ*DA’/PA’ = PQ*CA’/AA’DE = PQ*AB/(AA’*AR/BS-AA')
【術曰:以勾高乘東南隅入下股,如上股而一,所得減勾高,餘為法;以東北隅下股減東南隅下股,餘以乘矩間為實。實如法而一,得邑南北長也。求邑廣:以入橫勾乘矩間為實。實如法而一,即得邑東西廣。】
【勾高】=AA’,
【東南隅下股】=AR,
【上股】=BS,
【東北隅下股】=AP,
【矩間】=AB,
【入橫勾】=PQ,
式子完全吻合!
【今有登山臨邑,邑在山南。偃矩山上,令勾高三尺五寸。令勾端與邑東南隅及東北隅參相直。從勾端遙望東北隅,入下股一丈二尺。又施橫勾於入股之會,從立勾端望西北隅,入橫勾五尺。望東南隅,入下股一丈八尺。又設重矩於上,令矩間相去四丈。更從立勾端望東南隅,入上股一丈七尺五寸。問邑廣長各幾何?】
【勾高】=AA’=3尺+5寸=3.5尺,
【東北隅下股】=AP=1丈+2尺=12尺,
【入橫勾】=PQ=5尺,
【東南隅下股】=AR=1丈+8尺=18尺,
【矩間】=AB=4丈=40尺,
【上股】=BS=1丈+7尺+5寸=17.5尺。
得:DG = (AR-AP)*AB/(AA’*AR/BS-AA’) = (18-12)*40/(3.5*18/17.5-3.5) = 240/0.1 = 2400DE = PQ*AB/(AA’*AR/BS-AA’) = 5*40/(3.5*18/17.5-3.5) = 200/0.1 = 2000
【答曰:南北長一里百步;東西廣一里三十三步、少半步。】
【南北長】= 1裏 + 100步 = 1800尺 + 600尺 = 2400尺
【東西廣】= 1裏 + 33步 + 1/3步 = 1800尺 + 198尺 + 2尺 = 2000尺
結果完全吻合!
參考資料:
《海島算經》討論組,百度貼吧,網友毒酒滴凍鴨;