諾獎委員會萬字評述:為什麼複雜系統研究受諾貝爾物理學獎青睞?_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2021-11-09 11:17

諾獎頒佈的同時,諾貝爾獎委員會在官網提供了一份15頁的文檔,詳細梳理了三位學者的相關工作,討論了他們對於理解複雜系統的開創性貢獻,並揭示複雜系統理論和跨尺度通用方法對解決氣候變化等全球系統性問題的重要意義。集智編輯部組織翻譯諾獎委員會評述的全文,以饗讀者。
撰文 | 諾獎委員會
翻譯 | 王百臻、郭鐵城、Leo、梁金、劉培源
目錄:
I. 引入
II. 氣候物理:背景與歷史
III. 不同模型的發展
IV. 用觀察來測試模型
V. 潛力無限的無序世界
VI. 總結
I. 引入
今年的諾貝爾物理學獎聚焦於物理系統的複雜性,從人類所經歷的最大尺度,如地球氣候,一直到神秘而又普通的材料中所藴含的微觀結構和動力學,如玻璃。科學家們明白,對任何事物的單一預測都不能被視為無懈可擊的真理,如果無法瞭解可變性的起源,我們就無法理解任意一個系統的行為。例如,直到我們瞭解了這種可變性的起源,我們才能理解:全球變暖是真實存在的,並且歸因於人類。在本文中,我們將從較具一般性的學術背景出發,為討論這些具體的學術貢獻提供一個基本的語境。我們將要關注的一個核心問題這樣一個物理現實,即從氣候動力學到阻挫材料等一系列基本過程的變化導致了多個空間與時間尺度的出現。因此,這對於理論、實驗和觀測的解釋至關重要。
A. 不穩定性和非線性是多尺度複雜性和隨機性的基礎
從秩序到無序的湧現,以及隨之出現在空間和時間上的多重尺度,是複雜系統的一個特徵。理解這種無序的本質是一個艱難的科學挑戰。它很自然地包含着以下問題: 這種無序是否會生長?它的時空範圍是否是無界的?這種無序會選擇一個特定的空間結構,還是許多彼此相異的空間結構?這種選擇是否涉及一個系統的所有自由度,亦或是僅僅其中一個子集?如果只涉及一個子集中的情況,那麼具體會是哪個子集?
這些問題本身具有與它們所涉及的現象相同程度的多尺度結構。
一個經典的例子是層流向湍流的轉變。但是在這個系統以及其他類型的非線性系統中,描述橫亙在有序和無序之間的邊界是物理學中最具挑戰性的問題之一。事實上,多尺度物理學層面的解讀已經在湍流的理論和實驗方面有了突出的進展。並且我們可知:統計物理學和流體動力學不穩定性之間的聯繫構成了這個問題一般性的基礎。
湍流熱對流(例如我們將水煮沸時發生的情況)是一個理想環境,可以用來證明各種尺度在控制熱量和質量的宏觀輸運上所起的作用。當洛倫茲(Edward Lorenz)建立旨在描述大氣對流的"玩具模型"時,他就是這樣想的。“玩具模型”是瑞利-貝納德對流(Rayleigh-Benard convection)方程在無應力邊界條件下的一個Galerkin截斷。模型具體如下:
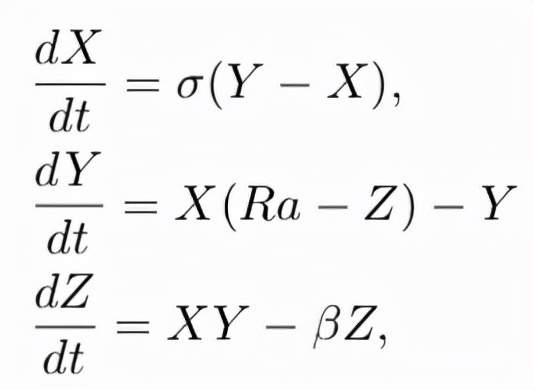
洛倫茲系統是低維混沌中一個經典的玩具模型。鑑於該模型的起源以及其研究的廣度是如此廣泛,我們很難在這裏將這些研究全部列舉出來。關於該系統的一個關鍵事實是:該模型的解是有界的,但它的解表現出了對方程初始條件的敏感依賴性。
龐加萊發現三體問題的長期行為比預期中要複雜得多,並因此被認為是這個領域的開創者。用現代的説法講,他觀察到同宿軌道的纏結(tangling)現象(這是一個動力系統的軌跡,該軌跡將鞍平衡點連接到自身,位於平衡的穩定流形和不穩定流形的交叉點)並推斷出運動方程微擾解的發散性。他認識到,太陽系可以被動態地看作是可積開普勒問題的一個擾動。
統計力學和流體動力學中那些令人振奮的遠大圖景依舊在繼續激勵並挑戰着研究者們。從系統相空間的角度看,原則上,我們可以通過玻爾茲曼、Fokker-Planck或劉維爾方程來獲得對系統概率密度演化的完整描述,但這種高維偏微分方程可能難以得到具有實際意義的分析結論。相比之下,低維常微分方程可能會表現出令人震驚的複雜混沌動力學。然而,無論是在抽象形式上還是針對特定的物理系統中,例如那些大氣動力學系統,有效的動力學系統可能會在較低維度的低速流形(slow manifold)上運轉。因此,我們有理由問出如下這個問題:氣候(信號)是否是天氣(噪聲)的低速流形?當然,這樣一個問題是今年獲得榮譽的成果中的核心工作,並在更加廣泛的非平衡系統中被提出來。在這些非平衡系統中,氣候和天氣被其他系統所取代。這類問題中的一個關鍵是,如何區分內部、外部和突發現象。
B. 隨機性和無序性可推導出可預測性
經典布朗運動假設信號與噪聲之間處於均衡關係,並一直處在熱平衡之中。然而,在失去平衡的系統中,情況可能截然不同。喬治·帕裏西(Giorgio Parisi)強調,平衡系統和非平衡系統之間的區別如下:
“但對於僅僅只是略微失衡的體系而言,情況就不同了。例如,我們可以想象一個系統由於高自由能障礙(可能是能量障礙或熵障礙)而無法達到平衡態:這種情況通常適用於無序系統,如自旋玻璃和結構玻璃。這樣的系統將從一個亞穩態跳躍到另一個亞穩態,從而慢慢接近平衡態。如果系統不斷受到緩慢變化的外場干擾,它可能永遠保持輕微的失衡狀態。在這樣的系統中,我們可以預期系統的微觀時間尺度(例如單個原子的振動)和跨越障礙所需的宏觀時間尺度(例如系統本身結構的變化)之間會有着許多不同數量級的分層。我們可以進一步認為:該系統基本上是在亞穩態內熱化的,因此仍然可以應用漲落耗散的思想:緩慢變化的系統總體狀態被認為是一個小擾動。”
這種基本的思維模式是今年被認可工作的主要特徵,無論是對於自旋玻璃,還是對於其他任何複雜的隨機多尺度系統(例如氣候)。事實上,至關重要的一點是理解以下事實:噪聲和無序性能夠影響所有系統,並且能全然決定一些非線性動力系統的命運。因此,當噪聲引起可變性的根本原因被忽略時,什麼是可預測性也就變得似是而非了。
II. 氣候物理:背景與歷史
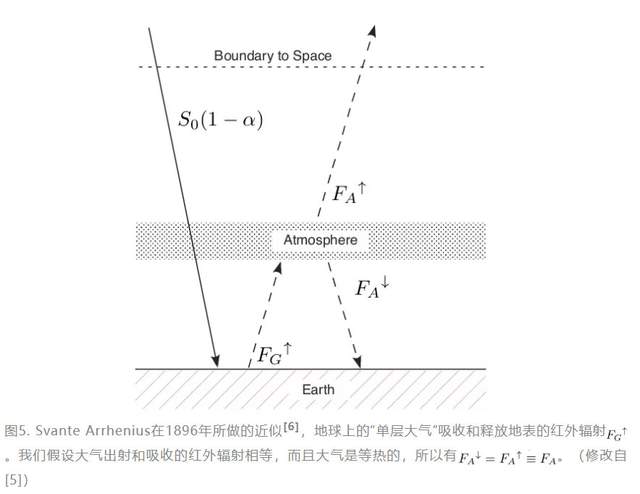
自從傅里葉 (Fourier) 開始研究地球的能量耗散與吸收以來,我們就知道短波太陽輻射是氣候系統的主要能量輸入來源。輸入主要在可見光波段,輸出在紅外波段,光譜的這種偏差決定了任何一個大氣吸收紅外線的行星的宜居性。Eunice Foote 測量了二氧化碳 (CO2)和其它氣體對太陽輻射的吸收而導致的加熱效應。1861年。John Tyndall 進一步發表了一個精彩的工作[109],系統地總結了包含水蒸氣和二氧化碳在內多種氣體對紅外輻射的吸收與輻射。這為未來“温室氣體”的研究提供了實驗基礎,同時也是 Svante Arrhenius [6](1903年諾貝爾獎獲得者)於1896年取得重要進展的一個關鍵因素。我們會在下面談論更多關於Svante Arrhenius的工作。
除了氣候物理學中其他起關鍵作用的物理因素,地球大氣對紅外輻射的吸收與出射是物理學與計算方面極具挑戰的一個研究領域,與行星物理具有廣泛的相關性 [91]。Archer 和 Pierrehumbert 收集文獻中的主要觀點,並描述了物理氣候科學的歷史[4]。確實,我們現在可以輕鬆地在線運行輻射轉移模型 (radiative transfer model) ,這種操作的便利程度可能讓 Tyndall 感到震撼。我們會在下文介紹輻射轉移模型。
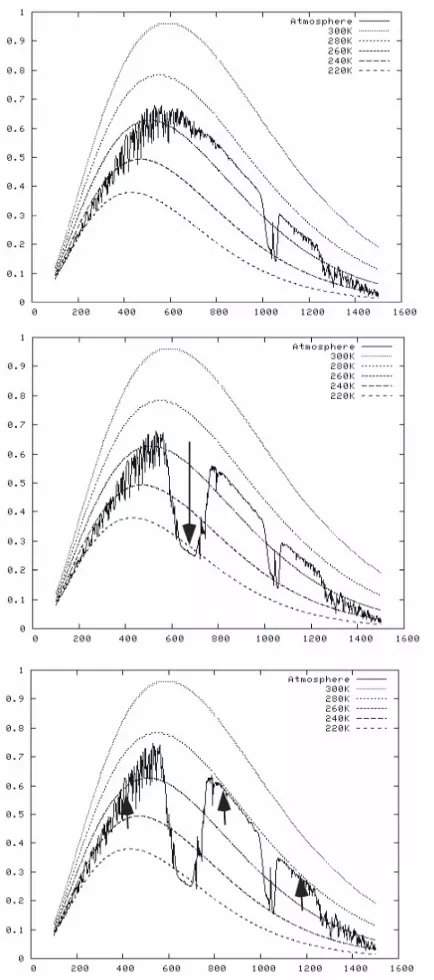
圖3展示了中等分辨率大氣傳輸(MODTRAN)模型的結果。MODTRAN 模型模擬了地球大氣紅外輻射的出射與吸收。當大氣中二氧化碳增加,逃逸到空間中的紅外輻射在譜中間區域降低(如中間子圖所示):波數為650 cm-1的位置像是被咬了一大口,這正是由於行星向外輻射通量降低所致。水蒸氣主導波譜直到大約500 cm-1,然後在更大波數再次主導。在大約1050 cm-1位置處出現的更小的被咬掉一口的形狀是由於臭氧。為了建立穩態能量平衡,在這個位置兩側、由水蒸氣主導的形狀像“翅膀”一樣的區域,必須在更高温度輻射。在這個例子中,地表温度增加了 8.5°C。
圖3中所看到的譜提示我們,地球大氣中最強勁的温室氣體是水蒸氣,而水蒸氣的分佈是我們無法控制的,我們不可能“控制”雨何時何地降落以及具體降水多少。其實,複雜的水文循環在控制大氣中的水蒸氣,基礎熱力學已經證明,温度每上升 1 度,大氣中就可以多承載大約 7% 的水。這就是所謂的水蒸氣反饋 (water vapor feedback) 。隨着行星變熱,大氣中的水蒸氣含量增加,進一步使得温度增加,如此反覆遞進,温度不斷上升。通過水文循環的作用理解水蒸氣的分佈是一項巨大挑戰。
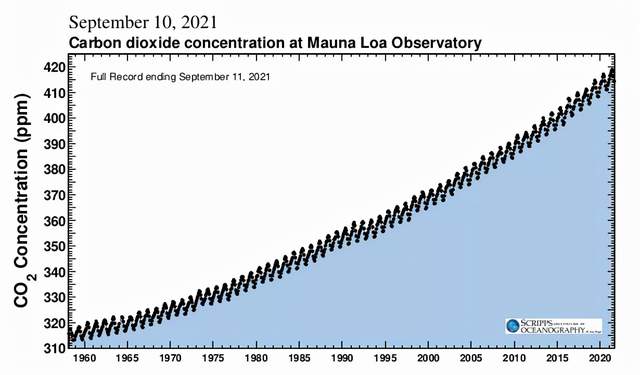
原則上,我們可以通過控制其它温室氣體的含量來控制地球的温度。很容易想到的簡單問題是:大氣二氧化碳的增加會對全球物理氣候學帶來什麼影響?正如物理科學中大多數看似清晰的問題一樣,通往答案的路徑是曲折的,成功往往與失敗和錯誤相伴。圖4的基林曲線 (Keeling Curve) 展示了主要觀測結論。該曲線是標誌性的,不僅具有分析精度,而且藴含着有價值的預示信息。在過去8個冰川期中——大約80萬年——二氧化碳濃度從未高於300 ppm,在冰川期-間冰期的最大變化為大約130ppm,温度反常大於10度[25] 。在曲線中包含如此多鋸齒的情況下,我們應該如何建立一個模型來描述這樣一個系統呢?
III. 不同模型的發展
A. 能量平衡模型(Energy balance models)
對氣候系統而言,太陽的能量輸入是最大的外部年度週期性熱驅動來源。鑑於此,我們現在知道:任何關於氣候的數學理論必須依賴於含時微分方程,來捕獲氣候子系統在許多時間尺度上的時間演化。另一方面,數值建模推進了天氣預報模型中整個系統的耦合方程,可以各種各樣的方式將含時驅動力包含進來。顯而易見的是:大氣、海洋、冰凍圈、陸地和生物圈必須遵循熱力學定律。然而,全局耦合系統中大量的時間尺度,使得確定一個給定時間尺度上某個子系統處於何種平衡成為一個很大的理論挑戰。

Arrhenius 的預測現在被稱為“氣候敏感度”,是為了估計當大氣二氧化碳濃度加倍時,地表温度 TG 會如何變化。現在的估計範圍為2.5-4°C,Arrhenius 預測為大約6°C。這種差別是由於當時吸收譜精度的限制以及圖5中對大氣模型的粗糙描述。隨着現代光譜學的發現,由於前文所述效應——二氧化碳影響與上層冷大氣相關的輻射到空間的紅外譜範圍——沒有被包含進來,所以導致後面的近似低估了氣候敏感度。這種低估被他所用的譜數據所修補。
Arrhenius 也關注現代物理氣候學的其它重要部分,特別是赤道-極點能量不平衡和冰反射率反饋 (ice-albedo feedback) 。對於後者,在式(1)中反射率與緯度相關意味着,氣候系統最基本的兩個狀態——冷和熱——與北極快速演化的冰塊緊密相關。確實,他對冰期的二氧化碳濃度做出了完美的預測:預測數值為 150 ppm,而從冰芯研究[25]可以知道二氧化碳濃度為180-200 ppm。他也對人類燃煤消耗如何導致大氣二氧化碳濃度加倍做出估計。所有這些都包含在 Arrhenius 的一篇文章中,他在其中為現代以各種不同形式使用的大氣柱模式提供了概念框架。從這種意義上説,人們知道温室氣體對氣候的影響已經有一又四分之一個世紀了。Arrhenius 的工作是偉大的預知,並且為今天的分析提供了基本要素。可以參考 [4] 中的討論。
B. 廣義的確定性能量平衡模型(EBMs)
正如在§III A小節所介紹的那樣,最簡單的模型處理整體平均,主要關注大氣的輻射轉移特性。這些推廣到每年平均、地區(跨過緯度方向地帶)平均的量,引入緯度依賴的TG、α和子午線方向(經線方向)熱輸運。這個框架含有時間依賴的行星冰線以及空間冰反射率反饋。如果擾動使得冰蓋擴張,系統吸收的能量變小,由式(1)得到它會更快地變冷,冰繼續擴張,這將驅動變冷的反饋過程。確實,這個理論預測,只要當太陽輻射通量 S0 低於幾個百分點時,就會急劇轉變到一個完全冰覆蓋的地球,一個“雪球”。一種解析方法[79]可以找到三個不動點;雪球和間冰期(當下的狀態)都是穩定態,近似三分之一冰覆蓋則是不穩定態。對於這類理論可以利用譜方法求解,正如數值求解 Navier-Stokes 方程所用到的譜方法[77]。
儘管人們很早就得到冰河時期清楚的觀測證據[2] ,一系列 EBMs 模型所預測的多種全球氣候狀態卻被看做是不真實的理論預測。然而,現在對“核冬天”——核武器引起的煙塵阻擋太陽輻射——的關注也成為了他們預測的興趣。直到最近幾十年人們才發現大約 7億年前的新元古代時期發生的冰川作用[54, 100],這也體現了 EBMs 模型[15, 101]作為定量工具所發揮的作用。
重要的是,這些理論捕獲了氣候系統的很多可能的態,並且包含很多出現在不同物理問題中的數學上有趣的推廣的特徵。正如 §III D 小節所展示的那樣。從這一層意義上來講,氣候科學促進了其他物理領域的研究。
C. 數值氣候模型的出現
1. 序曲
所有的模型都是對現實的近似。近似也就意味着,不管是數學解析還是對公式的數值求解,都會在特定的極限條件下失效。科學的藝術就在於對現實給出合理的近似,只有明確了模型失效的精度,我們才可以定義所謂“嚴格”。因為大型計算設備的獲取日益方便,氣候科學中“模型”一詞幾乎等價於全球氣候模型 (Global Climate Models, GCMs) ,而不是 EBMs 。當代的 GCMs 將大氣、海洋、冰系統參數化並表示為次網格尺度(sub-grid scale)的物理過程(比如 [38] ),通過數值求解質量、動量和能量守恆來進行處理。一些現代的方法利用數據同化 [94],測試高分辨率機制[52]來改進 GCMs 模型。
由於氣候(特別是流體)系統的複雜本質,GCMs 是目前發展的最複雜先進的數值模型。儘管如此,完全解決氣候系統中的時空過程依然是一個挑戰,特別是對於高緯度位置[1]。因為 GCMs 模型的複雜結構和處理的高維數據,抽取不同時間尺度上的主要物理過程並不是很直接,也無法解釋它們之間的相互作用。因此,GCM 像是巨大的粗粒化的天氣預報模型;全球氣候由所有已知物理過程和次網格尺度過程參數化的計算近似結果所代表。氣候模型的最新進展系統地包含了克勞斯·哈塞爾曼(Klaus Hasselmann)最早發展的概念[42]——天氣的混沌動力學帶來長時間尺度的變化,這必須包含在模型中[11, 20, 29, 59, 80, 81]。
2. 起源
入射太陽能與出射紅外能量的差是關於緯度的函數,在40°N和40°S之間有 5PW (千萬億瓦)的超出。能量通過大氣和海洋的運動傳輸到高緯度地區。因此熱量的大小和分佈與旋轉系統中流體的運動和混合緊密相關。大氣承載着 5PW 能量的三分之二,剩餘的由海洋傳輸,但是在不同時間尺度,並且受地理環境影響。因此理論與模型在現實中受制於這些因素,並且由於冰反射率反饋的原因,冰凍圈也會受到影響。
1950年,普林斯頓高等研究院的 Jule Charney 和馮·諾依曼 (John von Neumann) 領導了一個大規模數值天氣預報項目[19]。這自然地與研究大氣和海洋動力學的細緻過程的理論和實驗研究——地球物理流體動力學 (geophysical fluid dynamics, GFD) [114, 115]—— 同時發展。隨着時間發展,GFD、天氣預報和氣候建模之間存在文化差異,並且產生了不同學派,儘管方法不同,但它們都有共同的目標。
包括 Bert Bolin 在內的很多先驅都被招募到這個項目中來,或者來訪問,為這個項目帶來了專家經驗[112] 。這裏的關鍵是美國氣象局大氣環流實驗室的負責人 Joseph Smagorinsky 的參與。他後面去到了普林斯頓地球物理流體動力學實驗室,並在 1959 年招募了真鍋淑郎(Syukuro Manabe),1961 年聘請了 Kirk Bryan。實驗室很快聚集了大量程序員。
直到 1960 年 Cecil E. Leith 獨立開發了現在公認的第一個完整的僅針對大氣的 GCM (AGCM) ,歷史細節可以在最近的一篇文章[39]中找到。該模型包含更低的平流層,以及對水文循環和雲的表示。Leith 給出程序運行的演示,並且站在計算機可視化的前沿。
3. 關鍵結果
數值模型[61-63]基於固體物理,並且可以看做 Arrhenius 設想的首次實現。更早的重要研究[60, 75]關注如何將已知的動力學和輻射過程包含進柱模式[62]。
真鍋淑郎和 Wetherald [62]將整個大氣視為一維的柱,包含特定的相對濕度和温室氣體濃度。從初態系統演化,通過(a)輻射轉移,這可以通過温室氣體的譜進行計算,其中佔最重要權重的是水蒸氣;(b)對流調整,這個過程對垂直動力學進行如下參數化。如果一個柱僅通過輻射轉移演化,衰減率為~-15°C/km,遠遠大於觀測值。現在,絕熱衰減率為~-10°C/km,但是在大氣中隨着空氣升高水凝結會釋放潛熱,這解釋了觀測到的“濕潤”衰減率~-6°C/km。為了對該現象進行建模,只要温度與濕潤衰減率有所偏差,表面加熱便會驅動垂直運動、相變和與之相伴的熱釋放。這就是真鍋淑郎和 Strickler [61] 的對流調整機制。
真鍋淑郎和 Wetherald [62]注意到,北半球的氣候緯度相對濕度的數據幾乎沒有季節性依賴變化,而絕對濕度(飽和蒸汽壓)敏感地依賴於温度。因此,他們 [62]重複了真鍋淑郎和 Strickler[61]的計算,關鍵的區別在於後者(更早的)文章使用了相對(絕對)濕度的分佈,很好地捕獲了上面所討論“水蒸氣反饋”。正如圖 5 的註解所述,大氣上層輻射到更低温度的空間,為了使能量平衡,必須捕捉相對濕度(包括最重要的温室氣體)、其他温室氣體的濃度和温度。這種彙集效應導致真鍋淑郎和 Wetherald [62]所給出的重要結果,即大氣二氧化碳加倍導致 2.3 °C的變暖。
1975年,真鍋淑郎和 Wetherald [63]通過求解全球熱、質量、動量和輻射的耦合方程,很大程度改進了他們 1967 年的計算[62],這是他們的第一個GCM,當時利用的計算機是大約 0.5 MB 的 RAM。當二氧化碳從 300 ppm 加倍到 600 ppm,全球平均表面温度增加 2.93 °C。模型假設無海洋熱輸運、理想化的地形,以及雲層固定分佈。
正如 §III A 小節所描述的那樣,Arrhenius 引入了氣候敏感度的概念,這一概念直到今天依然發揮作用。然而,我們需要區分 Arrhenius 的概念,或者説區分平衡氣候敏感度(ECS)與瞬時氣候敏感度(TCS)的差別。ECS 預期二氧化碳立即加倍,然後計算新的穩態能量平衡,但達到穩態所需的時間幾乎完全不準確。對於一個極端情形,大氣二氧化碳從 0 ppm 增加到 1000 ppm ,如圖 3 所示,其中中等分辨率大氣傳輸模型 (MODTRAN) 模型被用來展示 ECS 的思想。MODTRAN 使用與真鍋淑郎和 Wetherald [62]同樣的方法,來模擬大氣中紅外輻射的出射與吸收,但是是利用現代的譜數據與方法。當二氧化碳釋放到大氣中,逃逸到空間的紅外輻射在中間譜段減少,這可以從中間子圖看出來。但是為了重新達到穩態,它旁邊的“翅膀”(水蒸氣佔據主要作用)意味着必須在更高温度輻射,因此地面温度會升高 8.5°C。該計算重新平衡了柱能量,正如真鍋淑郎和 Wetherald[62, 63]所做的那樣,並且需要新的地面温度來實現這一點。
當代 GCM 產生的氣候敏感度區間在 2.5-4°C,真鍋淑郎和 Wetherald 的兩個不同方法[62, 63]給出 2.3-2.93°C的結果。正如 §III A 小節所述,我們知道 Arrhenius 關於 ECS 的結果(大約6°C)為什麼是上限(吸收譜精度和等熱大氣),但是真鍋淑郎和 Wetherald[62, 63]結果的魯棒性是顯著的,這也預示着增加模型複雜度並不一定會提高模型的預測能力。實際上温室氣體是隨時間演化的,氣候的響應也是如此,這是 TCS 所藴含的。因此,瞬時氣候敏感度(TCS)確實影響着人類。ECS 和 TCS 都是模型依賴的,正是 Hasselmann 建議了一種機制來系統地評估模型與變化的觀測量相比到底如何,以及是什麼引起了兩者的變化。
D. 隨機理論 (Stochastic Theory)
行星大氣體現了在不同時間和空間尺度上的相互作用。短波輻射通量的空間不均勻性驅動大氣和海洋的流體動力學,通過流體對流和波傳播[31]導致長程聯繫。上面所述的 GCMs 儘量包含這些過程,但是大量計算來量化這些變化是持續的挑戰。因此如何從統計的中心極限定理的角度來量化可變性在觀測和理論研究方面都引發了濃厚的興趣。在這同一時期,真鍋淑郎和合作者們的確定性模型(deterministic model,不包含任何隨機成分)主要專注於構造 GCMs 模型。

1. Hasselmann 隨機框架簡述

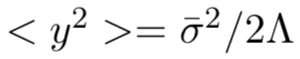
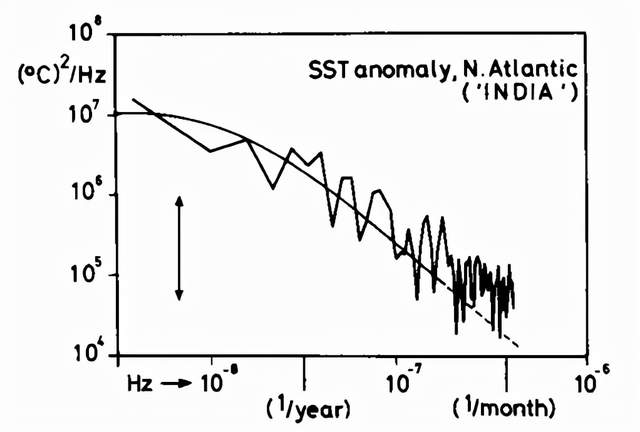
在圖 6 中,儘管隨着頻率減小,譜不斷增長,但因為有限耗散 Λ 的存在,我們期望它最終會達到飽和。然而,Hasselmann、Wunsch [131]以及其他人指出,海洋對時間有極其長期的記憶,可達成百上千年。此外,在與人類相關的幾十年時間尺度上,得到的證據與記憶時間無窮長時是一致的。因此,這表明存在一種可能的自相似或分形特徵,不同時間尺度提供不同類的隨機過程(例如白噪聲、粉噪聲、紅噪聲等)[72]。因此一個數據記錄是不穩定的態,具有變化的方差和不易測量的平均值,是 Hasselmann 類比布朗運動的工作中體現出的氣候變化的基本特點。
顯然這種方法可以推廣和應用到其他領域的很多方向去。然而,將氣候數據,以及氣候可預測性和變化視為隨機過程的理論框架可以追溯到 Mitchell[71]和 Hasselmann[42],後者成功將隨機方法應用到圖6中來自 Claude Frankignoul 的數據中。正如很多好的想法一樣,新的方法和想法可以從中產生,但它也有很多近似和限制。特別的,如上所述,識別出觀測數據中不同的譜隙可以證明時間尺度分離的假設,但這依賴於所使用的數據。
儘管如此,由於 Hasselmann 的理論, 對於氣候變化的典型的零假設是紅功率譜(紅噪聲對應的功率譜,高頻減少,低頻權重更大) [65, 113]。
IV. 用觀察來測試模型
從實驗室科學的角度來看,使用實驗測量來檢驗理論是科學方法中不言而喻的一步。然而物理宇宙學(physical cosmology)和物理氣候學(physical climatology)是觀測科學——研究者觀察到的是自然所允許觀察的。
在衞星時代前的幾十年,理解大氣和海洋的動力學依賴於稀疏的觀測。例如在國際地球物理年(1957-1958)之前,當大規模系統觀測計劃啓動時,大部分理論和觀測重點都集中在諸如兩極[58, 110]之類的區域,或是諸如墨西哥灣流之類的洋流行為,以及普遍的海洋和大氣環流理論(由Jacob Bjerknes,George Carrier,Walter Munk,Carl Rossby 和 Henry Stommel等人的理論推動)。這些問題突破了數學和數值建模的界限。事實上,§III C中討論的普林斯頓高等研究院的數值預測小組,其成立的部分原因正是由於缺乏觀測數據。
正如1922年諾貝爾物理學獎得主尼爾斯·玻爾(Niels Bohr)所言,“預測是非常困難的,尤其是關於未來的預測!”我們瞭解未來氣候的主要工具是由真鍋淑郎和他的同事們開創的 GCMs。人們預測,或者用該領域的術語説“設計”(project),然後等着看會發生什麼。當然,未來將永遠等待我們到來,但Hasselmann 的想法是通過模型和觀測來探究,是什麼情況導致氣候達到了當前狀態?是自然變化還是人類活動導致了温室氣體濃度增加?
A. 氣候的指紋識別
為了評估氣候模型是否忠實再現了自然變化的信號,Hasselmann對隨機氣候動力學的興趣自然而然地導致他創建了一個框架,來系統地比較氣候模型和觀測結果。這項工作體現在了 1979-1997 年發表的三篇論文[43-45]中。
Hasselmann在該系列的第一篇論文[43]中指出,儘管概念上類似於單一網格點的數據,但處理氣候信號的矢量場結構仍是一項挑戰。也就是説,在引用單一網格點的方法時,“響應模式作為整體或部分是否具有統計顯著性的問題,顯然無法通過這種方法解決”。他的工作提供了從純空間數據[43]到空間-時間數據[44, 45]的框架。重要的是,他展示了最優檢測技術如何揭示對氣候系統自然變異性或者“噪聲”本質的理解。也就是説,信號的檢測不一定與信號最強的部分數據有關,而是與噪聲最弱的數據部分有關,從而揭示出對系統各組成部分更加細緻的物理解釋。
指紋識別(fingerprinting)方法通過使用氣候模型運行,基於控制系統的物理學來識別氣候變化。所謂的最優指紋(optimal fingerprinting)方法是對多元迴歸的時空泛化,適用於氣候變化檢測和將變化歸因於外部強迫氣候信號。時空指紋(spatio-temporal)識別方法,例如温室氣體濃度隨時間的三維變化,提供了區分觀察到的變化和自然變化的手段。經過多年的改進[45-49],該程序遠比模型模擬與單獨觀測的比較更加嚴格、細緻和全面。
一個從由向量y給出的觀測記錄的過濾版本開始,迴歸採取標準形式y=Xa+u,其中矩陣X包含外部強迫或信號的估計響應模式,a是調整這些模式振幅的比例因子向量,u表示內部氣候變異性,通常假定它是一個具有協方差矩陣c的高斯隨機向量。矢量a是用各種統計技術根據c、X和y估計出來的,其中X包含使用GCM模型或EBM模型所估計的信號,以創建具有複雜時空結構的“內部可變性”(internal variability)。要想將觀測到的反應歸因於人為強迫,X必須包含單獨的自然和人為響應,因此必須説明強迫調整振幅以將模型與觀測結果相匹配的可能錯誤。通過這種方式,檢測和歸因是通過物理推理和評估關於a中的比例因子的具體假設來確定的。重要的是,結果依賴於對觀測結果的準確指紋振幅的估計,並且與所使用的氣候模型是否正確地模擬了指紋振幅無關 [例如49] 。
在最近的一篇“慶祝氣候變化科學三大事件的週年紀念”文章中[98],Santer和他的同事們回顧了自1979年《查尼報告(Charney Report)》[19]以來的40年間取得的進展,報告與Hasselmann關於“如何自洽地比較模型和觀測結果”的論文 [43]同年發表。Santer文章共有4個部分[98],第一部分是查尼報告的摘要,第二部分是Hasselmann最優檢測的論文[43]——作者稱之為“為確定人類造成的變暖信號提供可靠統計框架的首次嚴肅的努力”。這種方法與以往的單變量統計工作不同:
Hasselmann沒有選擇大海撈針然後去下個地方繼續撈,而是提倡一種更高效的測量——同時搜索整片大海。他還指出,理論、觀測和模型提供了大量有關信號和噪聲的適當聯繫的信息。這些獨特的信號特徵(或指紋)可以用於區分氣候信號和氣候噪聲。
查尼報告依賴基礎理論和早期氣候模型模擬,從中人們清楚地認識到化石燃料燃燒將明顯產生全球變暖信號[19]。Hasselmann的論文[43]概述了檢測該信號的合理方法。衞星搭載的微波探測器此後開始檢測大氣温度,提供全球數十年氣候變化模式和自然內部變化信息,這些是應用Hasselmann信號探測方法所需要的。
Hasselmann的論文是後來數百項氣候變化檢測和歸因研究的統計學路線圖,為IPCC在2013年得出的結論提供了強有力的科學支持:自20世紀中葉以來,人類的影響極有可能是觀測到的氣候變暖的主要原因。
V. 潛力無限的無序世界
A. 復型、自旋玻璃、阻挫
“自旋玻璃”這個術語是在20世紀70年代初被創造出來的,用來描述無序的磁系統,這種系統會發生相變,結果使得每個磁性原子都具有穩定的排列,只不過排列方向在原子之間隨機變化。想象一個三角形,三個角上各放着一個小磁體。磁體的北極可以向上,也可以向下。在直觀情況下,假設將三角形置於垂直於其平面的向上或向下的外部磁場中,我們可以想象這三個小磁體都指向上或向下。
現在如果我們施加一個“反鐵磁”約束,使得任何一對相鄰的小磁體必須具有相反的方向。當兩個磁體滿足約束條件時,另外兩個就無法滿足,無論如何翻轉磁體都無法滿足約束條件——系統遭遇了“阻挫”(frustrated)。這種極端理想化的設置是一種簡單的方法,可以用來觀察自旋玻璃和其他系統如何遭遇阻挫。
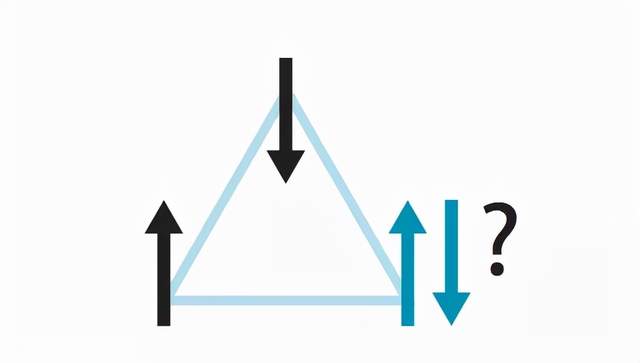
許多阻挫系統都以獨特的方式受挫,它們有很多選擇,包括“結構”或“普通”玻璃,“邊緣”或“Gardner”玻璃。我們並不打算專門討論各種玻璃系統,只是想強調這類系統的一個共同特徵:當迅速猝滅時,它們無法進入平衡態,而是會持續佔據大量非常長壽的亞穩態。
因此,一個給定的實驗系統通常有一個獨特的測量、數字和/或概念協議。從一開始,系統的特殊性就一直是該領域的主要挑戰[例如 12, 68, 96]。1977年諾貝爾獎得主菲利普·安德森(Philip Anderson)認為:“自旋玻璃的歷史可能是我所知道的這句格言的最好例子,即一個真正的科學謎題是值得追尋到地球盡頭的,即使不具有任何明顯的實際重要性或智識上的魅力。”(The history of spin glass may be the best example I know of the dictum that a real scientific mystery is worth pursuing to the ends of the Earth for its own sake, independently of any obvious practical importance or intellectual glamour. )[3]
B. 解決復型的對稱破缺問題

Giorgio Parisi 解決了復型對稱破缺的問題。他意識到,與鐵磁體在有序相中只有兩種“純態”(上/下)不同,自旋玻璃在有序相一定有無窮多個態[82, 83]。這不僅提供瞭解決方案,而且在自旋玻璃和其他系統中具有一系列出人意料的擴展 [68, 69, 84-86]。
為了實現無窮多個狀態,Parisi所做的重要突破是引入一個新的序參量:
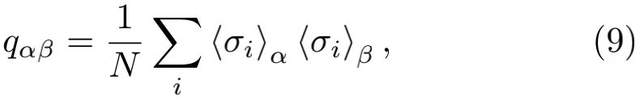
數學超出了我們的討論範圍。其中一個關鍵概念叫做超度量(ultrametricity),這是我們上學時就知道的三角不等式(三角形任意兩條邊的長度之和大於或等於第三條邊)的泛函版本。在這裏,超度量可以用一個描述系統狀態的網絡來刻畫,我們會發現,當隨機選擇三個狀態時,至少有兩個重疊是相等的,這樣重疊的無序平均分佈(disorder-average distribution)是
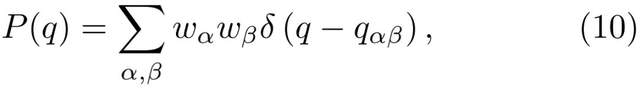
C. 應用和影響
自從 Parisi 的原創性工作問世以來,復型對稱破缺概念和方法的廣泛影響爆發式地增長。特別是,Parisi和他的合作者證明,在 John Hopfield 的神經網絡模型[50]及其眾多衍生模型中,存儲在網絡中的多重記憶與自旋玻璃的多重平衡相是對應的。
此外,復型方法讓我們能夠解決旅行推銷員這個經典的最優化問題。這個問題説的是,給定一系列城市和每兩個城市之間的距離,求解訪問每一座城市一次並回到起始城市的最短迴路,這個問題有許多局部極小值,而求解的目標則是全局極小值/最小值。[68]在這本書出版的時候,David Thouless寫道[107]:
我覺得研究自旋玻璃的專家們就像是在敵對地區紮營的定居者。他們做了一些有趣的觀察,但還沒有學會如何與那些更早的定居者交流。在一些關於神經網絡的論文中,幾乎沒有提及自旋玻璃社區之外的其他科學家的工作。
顯然,在此後的30多年裏,早期定居者在許多地方廣泛殖民。這包括 (a) 基本理解為什麼一些最優化問題很容易,而另一些很困難(見[70]和其中的參考文獻),(b) 為結構玻璃提供一個隨機的一階理論,(c) 給出硬球阻塞填充問題的幾何理論,這是平均場復型對稱破缺的一個極其成功的應用,從二維到無限維都適用[89]。該方法為經典顆粒物質[9]的實驗確立了標準,並在平衡和緩慢壓縮的詳細數值分析[16, 17, 95]中得到了證實[93]。
此外,在緩慢緻密化的膠體玻璃[37]中直接觀察到了玻璃復型理論所預測的邊緣相(marginal phase)。重要的是,在使用隨機激光器[30, 33, 99, 108]的系統中,在沒有無序、但相互作用的激光模式之間存在阻挫的平面腔激光器中[7, 74],以及通過光折變無序波導的非線性光傳播中[90],都給出了復型對稱破缺的實驗證據。
最後,隨機激光系統的性質允許對復型對稱破缺,以及自旋玻璃和湍流[34]之間的聯繫,特別是非線性波相互作用進行伴隨觀測,這將Hasselmann的早期工作[40]與Parisi的理論,以及無序和漲落在一般複雜系統中的作用聯繫起來。
隨機激光和復型對稱破缺
如上所述,公式(10)所預測的一階復型對稱破缺的雙峯特徵的一個激動人心的領域是在隨機激光中,其中受激發射以這樣或那樣的方式被介質複雜化[30, 33, 99, 108]。由於能量密度由泵浦功率控制,泵浦功率與温度成反比,因此,隨着泵浦功率增加,系統中的非線性將發揮類似於低温在玻璃形成過程中的作用,讓能量地形圖變得起伏不平。另一方面,當泵浦功率較低時,腔模表面上相互獨立,類似於自旋玻璃的順磁相。重要的是,隨機激光器有大量的亞穩態,而混沌激光器有少量的模式可以表現出指數路徑發散。這導致不同類型的激光具有不同的光譜特性。

我們討論了復型對稱破缺的實現,事實上,Parisi 通過漲落、隨機和無序的透鏡,揭示並發展了一系列物理系統之間錯綜複雜的聯繫,其中包括量子場論中的隨機性、湍流的間歇性、歐幾里德隨機矩陣、玻璃中的非平衡漲落、隨機界面運動、顆粒物質,以及隨機漲落在控制地球長期氣候狀態中的作用。
VI. 總 結
顯然,今年的獲獎者作出的開創性貢獻,有助於我們理解複雜物理系統的微觀與宏觀。他們的研究表明,如果沒有對無序、噪聲和可變性的正確解釋,那麼決定論就只是一種錯覺。事實上,本屆諾獎所認可的工作也部分反映了理查德·費曼(Richard Feynman,1965年諾貝爾獎獲得者)的評論——相信懷疑是首要的,這不是我們認識能力的缺陷,而是認識的本質(Believed in the primacy of doubt, not as a blemish on our ability to know, but as the essence of knowing)[32]。
這三位科學巨擘的工作表明,對任何事物的單一預測都不能被視為不可質疑的真理;如果不冷靜地探索變化的根源,我們就無法理解任何系統的行為。因此,只有在考慮了這些根源之後,我們才能理解——全球變暖是真實發生的事情,其原因也在於人類活動;我們在自然界中觀察到的大量現象都來自潛在的無序;而擁抱噪聲和不確定是通往可預測性的必經之路。