集合論 vs 範疇論 ＝ 彙編語言 vs C++？｜範疇論哲學 I_風聞

範疇論是現代數學中重要的一門學科，已經對人們理解現代數學和物理問題產生了深遠影響。簡單來説，這是一門研究“關係”及其性質的學問，是數學的數學。但作為一項極為抽象的理論，繁雜的技術細節會令人望而卻步。本文則從另一個角度，把範疇論作為談論數學的語言，闡述其對思維方式的影響。文章作者深受範疇論影響，舉出許多實例來輔以幫助理解範疇論的思想和哲學，希冀對我們理解範疇論，體會範疇的思考方式有所幫助。

撰文 | 葉凌遠

前言

不知道大家有沒有看過《降臨》，這是一部科幻電影，根據特德·姜的小説《你一生的故事》改編而成。裏面講述了人類和外星人初次接觸時的故事。這個科幻故事的立足點非常有趣，它基於一位語言學家和一位人類學家在 20 世紀中葉所提出的沙皮爾-沃爾夫假説（Sapir-Whorf hypothesis），有時也被稱為語言相對論（linguistic relativity）。假説的主要內容是，一個人所掌握語言的內部結構會影響其思維方式和對世界的認知，於是使用不同語言的人其思維方式就不盡相同。在筆者的認識中，數學在某種意義上便是一門語言，儘管其是抽象的，但正是藉助數學的抽象性，我們才能認識到客觀世界背後的普遍規律。

今天這篇文章希望為讀者介紹一下範疇論。範疇論的歷史很短，還不到百年。它的創立脱胎於桑德斯·麥克萊恩（Saunders MacLane，1909-2005）和塞繆爾·艾倫伯格（Samuel Eilenberg，1913-1998）在 1945 年發表的論文 General theory of natural equivalences。短短七八十年的時間，範疇論已經滲透進了現代數學的大多數領域，特別是代數幾何和代數拓撲。

對大部分人而言，範疇論並不應該被理解成數學的一個分支；在某種意義上，範疇論應該被理解為談論數學對象的語言。數學對象已是抽象的了，談論抽象對象的語言本身只會更為抽象。我想這也許也是許多人不喜歡範疇論的原因。但從沙皮爾-沃爾夫假説的角度來看，學習範疇的語言，本質上是在學習範疇的思考方式；而這樣的思考方式所帶來的力量是沒有掌握的人難以想象的——就像在《降臨》中，掌握外星人的語言就意味着對時間的理解達到了其他人難以想象的程度。僅以筆者個人的經驗來説，只有在學會了範疇的語言後才感到不同的數學對象和領域作為一個整體是可以被理解的。

儘管範疇論只有很短的歷史，但它已經發展成為了一門非常豐富的學科，有許多的技術內容。範疇論所帶來的洞見非常多，許多更加深刻的洞察也更為專業化。而在這篇文章中，我並不會介紹任何範疇論的技術細節，甚至都不會給出範疇精確的數學定義。我希望着重強調的是範疇論的思考方式，這才是對大多數讀者而言最有用的部分。範疇論所帶來的洞見非常多，但許多更為深刻的洞見也更為專業化。本文只在最基礎的層面講講範疇論對我們思考問題的方式所帶來的轉變，希望這能夠激起部分讀者的興趣，以致能夠更加深入地學習範疇論的內容。這篇文章凝結了筆者很長時間思考的積累，希望能對讀者有所啓發。全文共 9000 字左右。

什麼是範疇？這個問題放在不同的語境中會有不同的答案。早在古希臘時期，亞里士多德就寫過著名的《範疇篇》（Categoriae），探究能被人所認知的對象的分類問題。在現代數學的語境下，範疇有其另外的含義和精確的數學定義，但對其最基本的直觀是不變的：將一類相似對象聚合到一起便組成一個範疇。

我們從小學開始的數學教育似乎培養了這樣的觀念：我們總是更傾向於對某單個數學對象進行研究和學習。當我們拿到一個抽象的數學對象，無論它是某個拓撲空間，還是一個羣或者向量空間，亦或是一個光滑流形等等，我們可能想到的第一個問題便是這個對象是由哪些元素構成的。換句話説，我們大多數時候研究一個數學對象的方式是從其自身的內部結構入手。粗略地説，這是集合論給我們提供的對數學對象的基本思考方式。

範疇論提供了另外的思路：我們可以從對象之間的關聯來研究一個對象所具有的性質。一個範疇不是單單把一類對象放在一起就好了，這些對象之間還有許多不同的關係。我們可以把所有的羣放在一起構成羣的範疇，但羣與羣之間還通過羣同態相關聯；我們也可以把所有的拓撲空間放在一個構成拓撲的範疇，但拓撲空間之間還有連續函數相關聯。因此，更準確地説，範疇是一類物體和它們之間的關聯，或採用更數學的語言——態射——所構成的一個整體。我們可以把所有羣構成的範疇記為 Grp，把所有拓撲空間構成的範疇記為 Top。類似的，我們把所有的集合所構成的範疇記為 Set（從數理邏輯的角度，Set 可以理解為你喜歡的公理集合論系統如 ZF, ZFC, ZFC+CH，甚至是 ZF+Atoms 等等的一個模型）。

從我們原本已有的知識可知，許多定義可以等價的用對象之間的態射來表述。一個子羣可以等價地看作一個單的羣同態，一個羣的商羣（或正規子羣）可以等價地看作一個滿的羣同態；正如一個子集可以等價地看作一個單射，一個商集可以等價地用滿射來表述。

可能相比子結構和商結構更難以直接觀察到的是，我們遇到的大部分普適的數學構造都可以用對象之間的態射來表述。這裏僅舉一個例子。

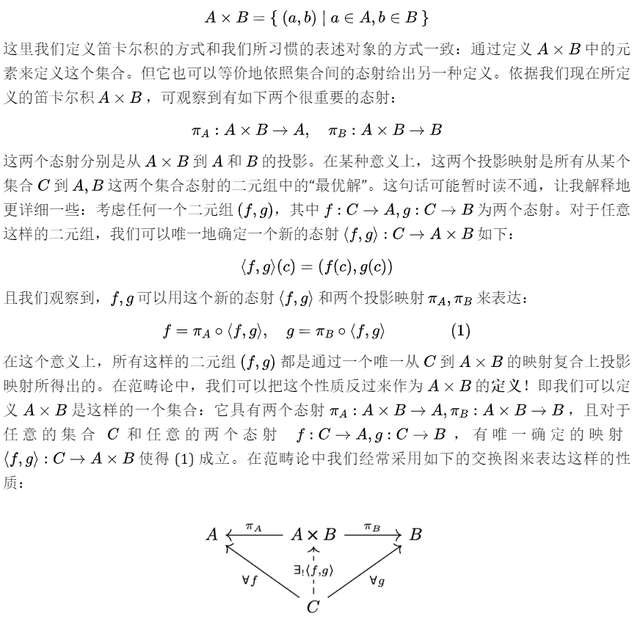
集合的笛卡爾積被定義為如下的一個集合：

我們可以有類似的總結：範疇論是根據功能（或者説與其他對象的關係)來定義和描述一般的對象的。

此處插一句題外話。上面提到的證明和泛性質之間的關聯其實反映了邏輯與範疇論之間更加深層次的對應。在某種特定的意義下（我必須要強調不是在所有意義下），邏輯和範疇是等價的。但這篇初步介紹範疇論思想的文章無法涵蓋這更深層次的聯繫。

粗略地説，這就是奠定整個範疇論基礎的 Yoneda 引理講述的內容：在一個範疇中，滿足同樣泛性質的結構之間必定是同構的（這只是對 Yoneda 引理的粗略描述，感興趣的讀者可以自行查找更為精準的表述）！用數學家的語言來説，泛性質在同構的意義上定義了笛卡爾積。

為什麼我們只希望在同構的意義上定義對象？或者更加廣泛地，為什麼採用泛性質、關注對象的功能和與其他事物之間的聯繫的思考方式對我們是更有用的？接下來僅僅列舉一些對我而言十分重要的原因。

數學關心的是“結構”而不是具體的某個“對象”

以範疇論為基礎發展出了一個數學哲學的流派，稱為結構主義（structuralism）。在此我特別強調，這一部分所敍述的不應該看作嚴格的哲學論述，只是為大家提供一個直觀而已，所以標題中的“結構”和“對象”均打上了引號。如果在數學哲學的語境下討論結構主義的觀點與內容，我們需要更為嚴謹的表述。

結構主義有關數學的一個基本論斷是，真正有數學實質內容的是一些“結構”，而不是某個具體的“對象”。這樣説起來非常抽象，讓我們舉一個例子來看看。或許我們最為熟悉的數學對象是自然數，在它上面我們能做基本的算術運算，例如加法、乘法等等。但如果你非常認真地看待集合論並認定它作為數學基礎的話，那你可能會問：這些自然數（比如 1）所對應的集合是什麼呢？這是一個可以合理問出的問題，因為在集合論的意義下一切數學對象均應該是一個集合。

歷史上數學家們給出了不同的定義。公理集合論的奠基人的策梅洛（Ernst Zermelo，1871-1953）定義瞭如下的集合作為自然數：

或許更為嚴重的是，一旦我們把單個自然數看作是一個確定的集合，由此會問出一些非常不自然且我們完全不關心的問題，比如“空集是否是 5 的一個元素”？在集合論的語境下，這是一個我們可以合理問出的問題，但這個問題的答案和我們理解自然數是無關的。

關於上面這個問題，一個更為數學的回答則是：這兩種自然數的定義都是合理的，具體採取哪一個取決於你的審美或你認為哪一個用起來更加方便。之所以這兩種定義（還有其他無窮多種定義）都是合理的，是因為這兩種定義下的自然數結構是同構的。換句話説，如果我們細心仔細的在這兩種自然數下都用集合論的操作定義好加法、乘法等數學運算，選擇哪一種進行運算必定不會對我們得到的結果產生任何影響。回到我們在這一節所強調的哲學上來，這説明我們關心的是自然數上這些加法、乘法等所具有的運算結構，而不是每個自然數自身的內部結構和構成。換句話説，任何與上面兩種定義的自然數同構的結構都是好的，我們只在同構的意義上關心自然數。

由之前的敍述可見，範疇論提供了一個非常自然的關心數學結構的環境：在範疇論的思考方式下，我們總是在同構的意義上考慮數學問題。這和數學真正運作的方式更加接近，同樣也非常有利於我們對問題的思考。我將在後一個部分更加深入地闡釋後面這一點。

在這一節的最後，我想再次説一説這種思考方式和邏輯之間的關聯。現代邏輯的思想本質在這一點上其實和範疇論非常類似；但在邏輯中，我們實現只關注“結構”而不是具體“對象”的方式是通過嚴格地區分語形（syntax）和語義（semantics）。

比如，我們同樣可以考慮在邏輯中如何認識自然數的問題。在數理邏輯的語境下，我們對自然數的刻畫是通過公理系統來實現的，比如皮亞諾算術公理系統 PA 或者其他 PA 的擴展，甚至是高階的算術系統。如果考慮某個算術系統，這個系統是從語法上來對自然數的結構進行刻畫，而不關心自然數的具體構成。例如，如果兩個結構之間是同構的，且其中一個是 PA 的一個模型，則另一個也自動地是 PA 的一個模型。

以此來看，邏輯上對語形和語義所做的區分和範疇論的思想是十分同步的。這個聯繫同樣有非常深刻的數學內涵，它標誌着我們的語形和語義之間的某種對偶，但可惜的是，無法在這篇文章有限的篇幅內介紹與此相關的更多內容了。

範疇論是數學的高級語言

基於前面提到的“結構”與“對象”的區分，我們以一個更加直觀的信息論的方式再來進一步説明為何範疇論的思想如此有價值。這一節我想要闡述的基本是如下的這個比喻：如果説集合論相當於數學的彙編語言，範疇論則相當於數學的高級語言。

這個比喻可能並不完全準確，因為對計算機來説彙編語言所能夠實現的，嚴格大於任何一個高級語言能夠實現的功能。但有許多數學家和哲學家卻認為範疇論本身能夠作為數學的基礎而存在（筆者本人其實對此持懷疑態度），不過這個比喻有助於我們理解範疇論的思想。同時直觀地來講，這也是一個宣傳範疇論有力的標語——我想畢竟只有異常少數的人才會喜歡彙編語言勝過 C++ 或 python。

從上面編程語言的比喻來看，對於任何一個日常的操作，彙編語言總是包含了很多我們不需要知道的冗餘信息。假設我們想完成一個讀取文檔內容的操作。若通過彙編語言的方式來實現，我們可能需要説明 CPU 線程具體的運行方式，且可能還需要指定讀取後的文檔具體存放在內存的哪一部分空間等等。我們最終得到的可能是一個相對較長的程序結構。但對於我們的目標而言，這些一切的一切我們都毫不關心；一般在任何一門高級語言中，可能只要一兩行代碼就能夠實現我們所需要的讀取文檔的功能，而剩餘的操作則由編譯器自動幫我們完成。

如果你對編程不熟悉，我再舉一個日常生活中的例子。在現代，我們對身邊許多物體的使用都是以功能為基礎的。我們知道手機可以用來打電話聊微信上網聽音樂，但我們從不會詢問這些功能具體是怎麼實現的。對日常生活來説，我們與這些東西的互動完全基於這些東西的功能；知曉這些功能是如何實現的不僅不會對我們的日常生活有任何的幫助，反而還會把事情複雜化，導致我們更難在紛繁複雜的細節信息當中找到對我們有用的部分。

更為重要的是，範疇論也並不在任何意義上阻礙我們探查更為細節的層面！反而，範疇論提供了非常好的工具讓我們在不同的語境下關注不同的內容。在日常生活的交互中，我們可以只關心手機的日常功能，但沒有任何理由阻止我們把手機拆開來看，關心各個手機模組是如何合作實現了某個具體功能的。在這個轉換中我們只是換了一個範疇來考慮：從手機與人類交流關聯的這個範疇轉移到了單個手機間各個模組相互交換信息的範疇！但即使在這個更為細節的範疇中，我們仍然有不想考慮的細節對象。比如我們希望把 CPU、電池、WI-FI 等模組作為整體來考慮，而不是考慮其內部二極管或其他電器元件的排布等，但我們也可以再度換一個範疇考慮與此相關的問題。

如果用一句話來總結，範疇論的基本思想反映了我們對“複雜信息的組織方式”。在現實世界中，這是非常行之有效的思考問題的方式。對數學來説，可能我之前所舉的例子都過於微不足道，以至於是否使用範疇論的語言對我們並沒有實質性的影響。但在我們面對現代數學越來越龐雜的數學對象時，你一定會發現範疇論的思考方式能夠極大地幫助你抓住問題的主幹，讓你的思考更有條理。

最後，我想説範疇論的思想不止停留在這個層面。如果只是對複雜信息進行分層，從原則上其實也並不一定需要採取範疇論的語言來完成這件事。但範疇論還包含了強大的工具幫助我們探究不同範疇或者説信息層次之間的關聯（回憶範疇論的基本哲學總是讓我們考慮對象之間的關聯）。實現這一點我們進一步需要函子（functor）和自然變換（natural transformation）等數學概念。感興趣的讀者可以進一步查詢文獻進行了解。

Knowing How V.S. Knowing Why

舉一個我身邊遇到的例子。我做凝聚態實驗的室友最近在學習拓撲。他在理解商空間的時候遇到了很大的障礙。在點集拓撲的語言下對商空間有一個利用開集寫下的定義，但這個定義較為複雜，用其證明一些商空間的性質就像是在做腦筋急轉彎。然而，商空間同樣有一個採用泛性質來進行定義的方式。換句話説，通過説明我們希望商空間所具有的功能，我們便能夠在同構的意義上確定商空間。更為重要的是，任何針對商空間基礎的、有意義的問題都能通過商空間的泛性質來進行解答。事實證明，我的室友發現泛性質要比開集的定義直觀很多，也更容易用其來證明有關商空間的結論。

為什麼會出現這樣的現象？我想這與我們常常感受到的 Knowing How 和 Knowing Why 的區別有關。從小學到高中再到大學，面對一道不會做的題，我們看到答案後往往會恍然大悟；從認識論的角度來看，針對這道題，在看到答案的時候，我們就有了 knowing how 的知識，即我們知道如何做這道題了。但同樣普遍的是，下次遇到一個類似的題目我們仍然不會做。這表明我們缺乏 knowing why 的知識，即這道題的答案為什麼要這樣做？或者我們為什麼要進行這樣的一個構造？

Universality

最後，我想接着上面談到的 knowing how 和 knowing why 的區別，談談範疇論對我們理解數學更進一步的幫助。大家回憶，我們在文章的最初舉到了不同的範疇的例子。有集合構成的範疇 Set，有羣構成的範疇 Grp，有拓撲空間構成的範疇 Top，等等。但如果考慮笛卡爾積的泛性質描述，你會發現範疇論定義的另一個巨大的優勢：我們並不依賴與某個具體的範疇給出了笛卡爾積的表述；相反，對任意一個範疇我們都可以根據泛性質的定義談論這個範疇中的笛卡爾積！如果你進行驗證，你會發現在羣論中定義的兩個羣的笛卡爾積，在 Grp 這個範疇下滿足我們上面表述的笛卡爾積的泛性質；同樣的，兩個拓撲空間的乘積拓撲在 Top 中也滿足笛卡爾積的泛性質！

這進一步表現了泛性質定義的兩個巨大的優勢。先談一談同樣與 knowing how 和 knowing why 相關的優勢。如果我問，為什麼我們的乘積拓撲空間所具有的乘積拓撲要如此定義？你可以思考一下你會怎麼回答。初學者可能説這是非常自然的；畢竟在歐幾里得空間中有着這樣的直觀。但隨着我們定義的數學對象變得更加複雜，我們的直觀很難繼續產生作用。比如對於無窮多個拓撲空間乘積的乘積拓撲定義便很大程度上不是直觀的。尋找這些 knowing why 的問題的答案同樣要回到我們的泛性質。和商空間的定義一樣，我們之所以要如此定義乘積拓撲和無限乘積的拓撲，是為了讓它滿足合適的泛性質。我相信對這一點的強調已經足夠了。

但更為重要的優勢是，範疇論在觀念層面統一了不同數學分支中的定義與概念。在範疇論發展之前，我們只有一個模糊地印象認為乘積拓撲、羣的笛卡爾積和集合的笛卡爾積是“類似”的，但範疇論使得我們進一步清晰地認識到它們之間具體的關聯：這些構造都是同一個概念在不同語境下的具體體現方式。這也是筆者為什麼對範疇論情有獨鍾的原因。現代科學發展的一個非常明顯的趨勢便是學科之間的劃分；不同領域的知識似乎被劃分地越來越精細，我們越來越難以對其有一個整體的認識與把握。但範疇論的出現部分地打通了數學在觀念層面上的分野，它找到了數學不同分支之間相同的觀念基礎！這實在是太難能可貴了！

最後的話

本文還沒有真正寫下範疇的定義，就已經講了如此之多範疇論的思想與哲學了，不知是否算是一個成功的嘗試；且一不小心字數可能過於得多了，只希望能對讀者有些許幫助。或許讀者可以從行文中讀得出來，筆者真的深受範疇論的影響，並真心地認同範疇的語言。本文大部分例子都看起來非常微不足道異常簡單，且可以肯定的是不借助範疇的語言大部分人也能夠掌握本文中提到的數學內容，但當之後面臨更加複雜的數學對象，你會發覺範疇的思考方式成為了必要。即使你不會面對那麼複雜的數學對象，範疇的語言也會讓你對數學有着更加整體的把握和理解，這始終是一個好事。

本文原文發表於知乎，經作者重新整理後發表於《返樸》。