"沒有免費午餐定理"加強版_風聞
code2Real-有人就有江湖,有code就有bug2021-11-16 09:25
經典的「沒有免費午餐定理」表明:如果某種學習算法在某些方面比另一種學習算法更優,則肯定會在其它某些方面弱於另一種學習算法。
也就是説,對於任何一個學習問題,沒有最優的算法,只有最合適的算法。
而在這項最新研究中,作者向我們揭示了這一現象背後的數學原理:每個神經網絡,都是一個高維向量。
在高維向量空間中,不存在單調的大小比較。如果兩個向量A、B是垂直的,則內積為零,通常也反映兩者更加不相關,比如作用在物體運動方向的垂直方向的力就不做功。
類似地,如果兩個神經網絡對應的向量內積為零,則反映它們的相似程度更低。
在擬合第三個向量C,也就是通過數據進行訓練和學習時,如果A和C內積更大,則表示A更容易學習C,也反映B更不容易學習C。
另一方面,當A通過訓練變得更加接近C時,與C垂直的另一個神經網絡D也會因此和A更加不相關,也就是A變得更加難以學習D。
此即本文提出的「沒有免費午餐定理」加強版。
利用這個數學描述,我們就可以量化神經網絡的泛化能力。
該研究主要基於寬神經網絡,而表示神經網絡的高維空間的每一個維度,都是由神經正切核的特徵向量構成的。
同時,作者也指出,該發現在寬度較小的網絡中也成立。在高維空間中,神經網絡泛化性的非單調數學關係一覽無餘。
複雜社會系統本質上也是高維向量,因此比較不同制度的優越性往往會導致自相矛盾的結論。想靠一種模式解決所有的社會問題是痴人説夢,估計只有元宇宙才能滿足這種夢想。
長期以來,探尋神經網絡泛化性能的量化方法一直是深度學習研究的核心目標。
儘管深度學習在許多任務上取得了巨大的成功,但是從根本上説,我們還無法很好地解釋神經網絡學習的函數為什麼可以很好地泛化到未曾見過的數據上。
從傳統的統計學習理論的直覺出發,過參數化的神經網絡難以獲得如此好的泛化效果,我們也很難得到有用的泛化界。
因此,研究人員試圖尋找一種新的方法來解釋神經網絡的泛化能力。
近日,加州大學伯克利分校的研究者於 Arxiv 上在線發表了一篇題為「NEURAL TANGENT KERNEL EIGENVALUES ACCURATELY PREDICT GENERALIZATION」的論文,指出「神經正切核」的特徵值可以準確地預測神經網絡的泛化性能。
「神經正切核」是近年來神經網絡優化理論研究的熱點概念,研究表明:通過梯度下降以無窮小的步長(也稱為梯度流)訓練的經過適當隨機初始化的足夠寬的神經網絡,等效於使用稱為神經正切核(NTK)的核迴歸預測器。
在本文中,作者指出:通過研究神經網絡的神經正切核的特徵系統,我們可以預測該神經網絡在學習任意函數時的泛化性能。具體而言,作者提出的理論不僅可以準確地預測測試的均方誤差,還可以預測學習到的函數的所有一階和二階統計量。
此外,通過使用量化給定目標函數的「可學習性」的度量標準,本文作者提出了一種加強版的**「沒有免費午餐定理**」****,該定理指出,對於寬的神經網絡而言:提升其對於給定目標函數的泛化性能,必定會弱化其對於正交函數的泛化性能。
最後,作者將本文提出的理論與寬度有限(寬度僅為 20)的網絡進行對比,發現本文提出的理論在這些寬度較小的網絡中也成立,這表明它不僅適用於標準的 NTK,事實上也能正確預測真實神經網絡的泛化性能。
 論文地址:https://arxiv.org/pdf/2110.03922.pdf
論文地址:https://arxiv.org/pdf/2110.03922.pdf
1
問題定義及研究背景
作者首先將上述問題形式化定義為:從第一性原理出發,對於特定的目標函數,我們是否高效地預測給定的神經網絡架構利用有限的個訓練樣本學習到的函數的泛化性能?
該理論不僅可以解釋為什麼神經網絡在某些函數上可以很好地泛化,而且還可以預測出給定的網絡架構適合哪些函數,讓我們可以從第一性原理出發為給定的問題挑選最合適的架構。
為此,本文作者進行了一系列近似,他們首先將真實的網絡近似為理想化的寬度無限的網絡,這與核迴歸是等價的。接着,作者針對核迴歸的泛化推導出了新的近似結果。這些近似的方程能夠準確預測出原始網絡的泛化性能。
本文的研究建立在無限寬網絡理論的基礎之上。該理論表明,隨着網絡寬度趨於無窮大,根據類似於中心極限定理的結果,常用的神經網絡會有非常簡單的解析形式。特別是,採用均方誤差(MSE)損失的梯度下降訓練的足夠寬的網絡等價於 NTK 核迴歸模型。利用這一結論,研究者們研究者們通過對核迴歸的泛化性能分析將相同的結論推廣至了有限寬的網絡。
Bordelon 等人於 2020 年發表的 ICML 論文「Spectrum dependent learning curves in kernel regression and wide neural networks」指出,當使用 NTK 作為核時,其表達式可以精準地預測學習任意函數的神經網絡的 MSE。我們可以認為,當樣本被添加到訓練集中時,網絡會在越來越大的輸入空間中泛化得很好。這個可學習函數的子空間的自然基即為 NTK 的特徵基,我們根據其特徵值的降序來學習特徵函數。
具體而言,本文作者首先形式化定義了目標函數的可學習性,該指標具備 MSE 所不具備的一些理想特性。接着,作者使用可學習性來證明了一個加強版的「沒有免費午餐定理」,該定理描述了核對正交基下所有函數的歸納偏置的折中。該定理表明,較高的 NTK 本徵模更容易學習,且這些本徵模之間在給定的訓練集大小下的學習能力存在零和競爭。作者進一步證明,對於任何的核或較寬的網絡,這一折中必然會使某些函數的泛化性能差於預期。
2
特徵值與特徵向量
令A為n階方陣,若存在數λ和非零向量x,使得Ax=λx,則λ稱為A的特徵值,x為A對應於特徵值λ的特徵向量。
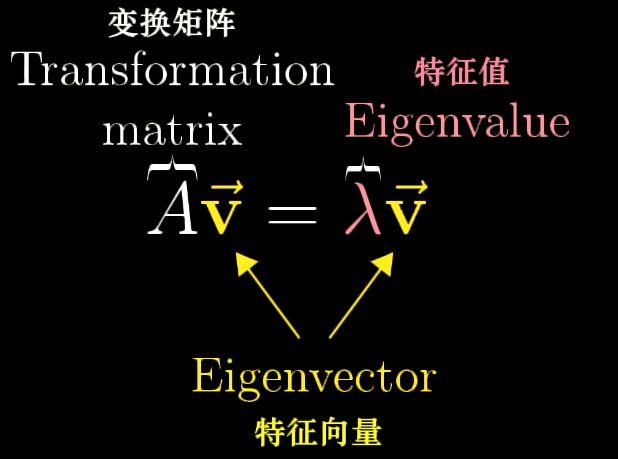 圖 1:特徵值與特徵向量的定義
圖 1:特徵值與特徵向量的定義
簡而言之,由於λ為常量,矩陣A並不改變特徵向量的方向,只是對特徵向量進行了尺度為λ的伸縮變換:
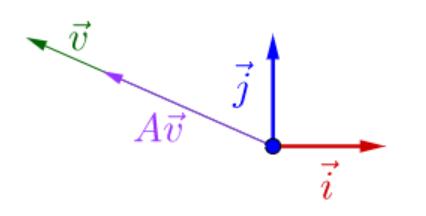 圖 2:特徵值與特徵向量的幾何意義
圖 2:特徵值與特徵向量的幾何意義
通過在特徵向量為基構成的向量空間中將神經網絡重新表示,我們得以將不同初始化的神經網絡以及學習後的神經網絡進行量化對比。
3
神經正切核
一個前饋神經網絡可以代表下面的函數:
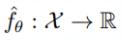 其中,θ是一個參數向量。令訓練樣本為x,目標值為y,測試數據點為x’,假設我們以較小的學習率η執行一步梯度下降,MSE 損失為
其中,θ是一個參數向量。令訓練樣本為x,目標值為y,測試數據點為x’,假設我們以較小的學習率η執行一步梯度下降,MSE 損失為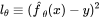 。則參數會以如下所示的方式更新:
。則參數會以如下所示的方式更新:
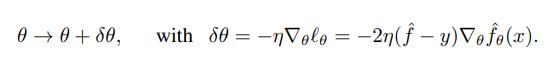 我們希望知道對於測試點而言,參數更新的變化有多大。為此,令θ線性變化,我們得到:
我們希望知道對於測試點而言,參數更新的變化有多大。為此,令θ線性變化,我們得到:
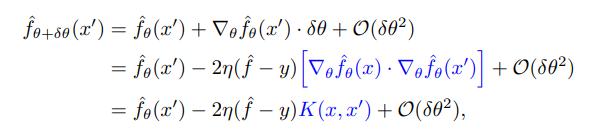 其中,我們將神經正切核 K 定義為:
其中,我們將神經正切核 K 定義為:
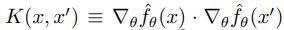 值得注意的是,隨着網絡寬度區域無窮大,
值得注意的是,隨着網絡寬度區域無窮大,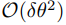 修正項可以忽略不計,且
修正項可以忽略不計,且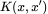 在任意的隨機初始化後,在訓練的任何時刻都是相同的,這極大簡化了對網絡訓練的分析。可以證明,在對任意數據集上利用 MSE 損失進行無限時長的訓練後,網絡學習到的函數可以歸納如下:
在任意的隨機初始化後,在訓練的任何時刻都是相同的,這極大簡化了對網絡訓練的分析。可以證明,在對任意數據集上利用 MSE 損失進行無限時長的訓練後,網絡學習到的函數可以歸納如下:
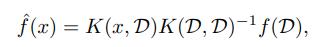 4
4
近似核迴歸的泛化
為了推導核迴歸的泛化性,我們將問題簡化,僅僅觀察核的特徵基上的學習問題。我們將核看做線性操作,其特徵值/向量對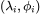 滿足:
滿足: