無愁河上的浪蕩漢子們|量子多體中的吶喊與彷徨之十一_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2021-11-19 11:13
撰文 | 孟子楊
來源 | 本文選自《物理》2021年第11期
 圖1 左圖:黃永玉畫的貓頭鷹,有多少人知道背後的荒唐歷史鬧劇;黃永玉創作的套色木刻《阿詩瑪像》(中),設計的猴票(右),都成為中國當代美術史上的經典作品
圖1 左圖:黃永玉畫的貓頭鷹,有多少人知道背後的荒唐歷史鬧劇;黃永玉創作的套色木刻《阿詩瑪像》(中),設計的猴票(右),都成為中國當代美術史上的經典作品
這個題目乍一看有點兒戲謔,甚至有些許少兒不宜的味道,其實《無愁河的浪蕩漢子》是木刻家、畫家、作家黃永玉在80多歲時開始寫作的以自己為原型的人生自傳,目前已經出到第三部。第一部《朱雀城》從傳主張序子兩歲開始,寫他的太婆、爺爺、父親母親、姑姑和表叔們——其中一位表叔就是寫出《邊城》、《長河》和《中國古代服飾研究》的沈從文——一個大家族,和他們生活的朱雀古城 (以湘西鳳凰為原型),古城的四季時光、風俗民情與繁華時的榮耀。在第二部《八年》中,家族和古城漸漸衰敗,十二歲的張序子也不得不沿着長河,漂流到外面廣闊的世界。八年中流浪歷險,正與中華民族抵禦外辱的生死時期重疊,少年張序子孤身遊走於閩東南一帶,見識到海洋文明的寬廣,在艱難中成長,奠定了一生的性情和藝術追求。在第三部《走讀》裏,活蹦亂跳的張序子娶了妻室,貨真價實地進入了成人世界,這一段生命之河已不能“無愁”,要真刀真槍搏生活、闖世界。在從贛州到廣州到廈門到上海到台北到香港的敍述中,可以看到一羣藝術家、文化人的性情樣貌以及各地的風俗人情,滿溢着時代、故園、骨肉的哀喜。但是,生活的磨礪並沒有改變藝術家們詼諧幽默的風格,在藝術上的孜孜以求,朋友們之間的互助,仍是書中主要描寫的內容。愛、憐憫、感恩,就是《無愁河的浪蕩漢子》的題旨。
畫家在後來的歲月中創作的貓頭鷹、阿詩瑪像還有生肖郵票中的猴票,都是當代美術史上令人難忘的有趣作品 (圖1),也折射出這個浪蕩漢子獨特的創造力和對於藝術的一片真心。尤其是想到這些作品是在怎樣的大背景下完成的,生活的沉重、時代的荒唐、現實的殘酷,是想躲都躲不過去的,而藝術家仍然是以赤子之心來面對,沉痛和堅毅之處往往讓人動容。黃永玉在《比我老的老頭》裏也寫過這樣的話:“我那時也曾哭過一次,忍不住的熱淚滂沱,頭埋在被子裏。那是讀到巴爾蒙特的詩句‘為了太陽,我才來到這世界!’哭得像小孩子。哭完就算,好人一個!”為什麼要哭,這背後的故事説起來太過複雜和辛酸,就像圖1中貓頭鷹的本事——真是一個傳奇的本事——感興趣的讀者可以自己查閲。對於我們的行文來説,重要的是要做到“好人一個”,藝術家、智者和這些有趣的人們集了自己一生的苦難經歷告訴我們,悲傷很耽誤時間,有人因此浪費了半輩子光陰甚至送掉了性命;把悲傷當成詩,那會好過點。重要的是要做有意思的事情,做自己認為有意思的事情,所有的事物和經歷都會成為滋養我們創造的養分。這就是無愁河上的浪蕩漢子。
科學家也可以有這樣的追求,也應該有這樣的追求。“認認真真地做一種事業,然後憑自己的興趣讀世上一切有趣的書”,總有些超越個體悲歡,超越時代的條條框框的有趣的事情,招引着、鞭策着和安慰着我們,讓我們也能漸漸成長為無愁河上的浪蕩漢子們。
講個具體的故事吧,還是我們自己的故事,一羣浪蕩漢子們的故事。
大家都知道以拓撲序和湧現分數化激發為代表的量子物質形態是當下凝聚態物理學和量子物質科學諸多研究方向的母題。在量子磁體和相變理論的領域中,如此的母題常常具象化為量子自旋液體的模型構造、數值求解和量子自旋液體態與常規的對稱性破缺態之間的相變行為的刻畫,當然如果有材料實現和實驗探測就更是錦上添花,這些都是當下研究的前沿 (參見前文:寂靜春天裏的動力學. 物理,2019,48(2):104) 。
在諸多阻挫磁體模型中,二維籠目 (kagome) 晶格的Balents—Fisher—Girvin模型 (簡稱BFG模型) 很受數值計算和解析理論同行們青睞。如圖2(a)所示,BFG模型每個kagome格點上有一個量子的自旋1/2自由度,用硬殼玻色子的語言來講,就是在每個格點上,S+、S-分別代表玻色子的產生、湮滅算符,Sz代表玻色子的佔據數算符。這個模型只有短程的兩體自旋 (或者玻色子) 相互作用,而不像有些拓撲序嚴格可解模型中複雜的多體和長程相互作用,即圖2(a)中最近鄰S+S- (玻色子的躍遷) 交換相互作用t和六邊形之內的SzSz (玻色子的密度—密度排斥) 阻挫相互作用V。為了實現Z2為偶的拓撲序,我們又在模型中加入相鄰六邊形之間的玻色子密度—密度排斥V ′。如此的模型既有Z2拓撲序量子自旋液體的基態 (Z2 quantum spin liquid,Z2 QSL),也有鐵磁XY長程序的基態(如果用玻色子的語言就是破缺玻色子U(1)對稱性的超流態 (super fluid,SF))。兩個基態之間的相變,不同於傳統的玻色—哈伯德 (Bose—Hubbard) 模型中從玻色子莫特絕緣體到超流態的(2+1)d XY相變,而因為此處的莫特絕緣體具有了Z2拓撲序和湧現自旋子 (spinon) 和vison任意子,相變類型變成了(2+1)d XY*,具有了不同的量子臨界描述。(見參考文獻[1—4]中關於這個模型和相圖的系列工作和系統描述。)
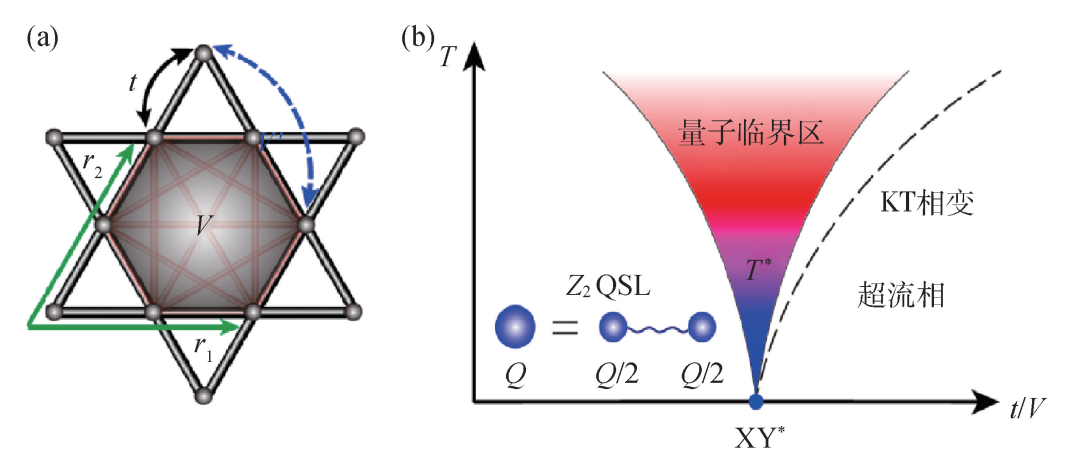 圖2 (a)Kagome晶格及BFG模型;(b)BFG模型的相圖示意圖:Z2量子自旋液體相(Z2 QSL)和其中的分數化電荷Q/2(spinon),超流相(SF)以及兩相之間的(2+1)維XY*相變點與量子臨界區。T *為湧現自對偶温度,臨界區中不同的温度區間(以不同顏色代表),與圖3中的温度區間對應
圖2 (a)Kagome晶格及BFG模型;(b)BFG模型的相圖示意圖:Z2量子自旋液體相(Z2 QSL)和其中的分數化電荷Q/2(spinon),超流相(SF)以及兩相之間的(2+1)維XY*相變點與量子臨界區。T *為湧現自對偶温度,臨界區中不同的温度區間(以不同顏色代表),與圖3中的温度區間對應
BFG這類模型還有一個好處,就是可以通過量子蒙特卡洛數值計算方法進行嚴格計算,得到如相變點、低能激發的譜函數等定量的信息,超越了微擾計算只能停留在“hand-waving”層面的尷尬情況。筆者與合作者等等一眾浪蕩漢子們之前的工作 (這裏需要特別提及的是現在在中國礦業大學材料與物理學院的青年教師王豔成,清華大學高等研究院的博士後孫光宇),就是運用蒙特卡洛計算和隨機解析延拓的數值計算方法,給出了這一類模型中的奇、偶Z2拓撲序自旋液體與其他對稱性破缺相的準確相圖[2,3],以及拓撲序自旋液體中的vison任意子激發在相變點上發生凝聚時,展現出來的拓撲序系統特有的平移對稱性分數化的譜學行為[4],為可能的中子散射實驗探測給出了理論憑藉(參見前文:寂靜春天裏的動力學)。
但是我們當時還有一個問題沒有回答,那就是在從Z2量子自旋液體到玻色子超流相之間的(2+1)d XY*相變點上,有沒有可以反映分數化任意子存在的跡象?雖然我們在前期的蒙特卡洛計算中已經看到臨界指數中的反常維度 (anomalous dimension) 從普通的(2+1)d XY相變中的0.04變為此處的接近1.5[3],但這樣的結果更像是少數理論工作者之間的黑話,對於廣大的只知道單體薛定諤方程的實驗凝聚態物理學工作者們來説,對於更多的從一隻貓的生死來理解量子糾纏、從事量子計算的理論和實驗科學工作者們來説,這個anomalous dimension還是太過抽象,聽不懂,此處需要有讓人能聽懂的信號。這樣的信號去哪裏找呢,我們這羣浪蕩漢子又浪蕩了好一段時間,才想到其實還真有,那就是電導(此處多虧浪蕩漢子中的一位,耶魯大學的程蒙老師,為大家指出這個方向),這才有下面要介紹的工作[1]。
其實拓撲序到目前為止真正的實驗系統實現,就是分數量子霍爾效應,而分數量子霍爾效應中的分數,就是指實驗上測得的二維電子氣體的霍爾電導是分數化的,如1/3,2/5,2/3等等。這樣的結果大家都熟悉。那麼在我們的Z2 QSL到玻色子SF的相變點上,是不是也有這樣的分數化電導呢?答案是肯定的。只不過此處的玻色子不帶電,所謂的電導不是電流的響應,而是玻色子粒子數流的響應。
其實在很多年前,人們已經知道在從玻色莫特絕緣體到超流體的(2+1)d XY相變點上,存在一個普適 (universal) 的電導值,而且這個universal的電導值還和(2+1)d XY相變共形場論描述中的基本常數有關係[5]。前期的量子蒙特卡洛與場論解析計算給出了在我們目前討論的單位下這個universal的電導值,σXY=0.3554[5,6] (後面會提及,此處的文獻[6]就是當時在中國科學技術大學讀博的陳錕同學和他的導師鄧友金老師等人的工作,他們的計算和分析方法對我們很有幫助)。而在我們的問題中,由於在相變點上玻色子整數電荷分數化為粒子數為1/2的自旋子,所以這裏用玻色子構造的電流算符變成普通的XY相變處電流算符的1/2,而電導就是從電流—電流關聯函數的測量中得到的,從而此處的電導應該分數化為普通XY相變電導的1/2×1/2=1/4倍。這就是我們所測定的在拓撲序的相變點上,電導分數化的意思。
當然,想想是如此,真正動手算起來,事情就不是那麼容易了。此處需要進行大規模量子蒙特卡洛模擬與理論分析相結合的研究方法,系統計算BFG模型在奇、偶Z2 QSL到超流相的(2+1)d XY*相變的量子臨界區裏的電導。好在我們從前期的工作裏面[3,4],已經比較準確地確定了零温相變點的位置,就是(t/V )c。然後又由於電流—電流關聯函數是動力學測量,我們需要在每個不同的計算温度下 (此處的温度或者虛時間,可以傅里葉變換為松原頻率),首先外插在每個頻率下電導在晶格尺度無窮大時的結果,然後再畫出外插所得的電導曲線,在每個温度下隨着頻率的函數。結果就是圖3(a),(b)中所示的一條條不同β=1/T (不同温度)所對應的數據點。這些繁複的分析,好在有前人在計算普通的(2+1)d XY相變點的電導時總結出來的操作規律[5,6],給了我們很大的啓發。但是BFG作為kagome阻挫磁體的基本模型,其量子蒙特卡洛計算和有限尺度數據分析,還是比正方晶格的量子轉子 (rotor) 模型困難不少。比如此處的温度尺度就比以往的計算要低起碼一個量級,這是因為在我們關心的Z2 QSL相中,系統的最低能任意子vison激發,其能隙很小 (這個後面會提到,其實還暗藏一個有趣的物理意義)。
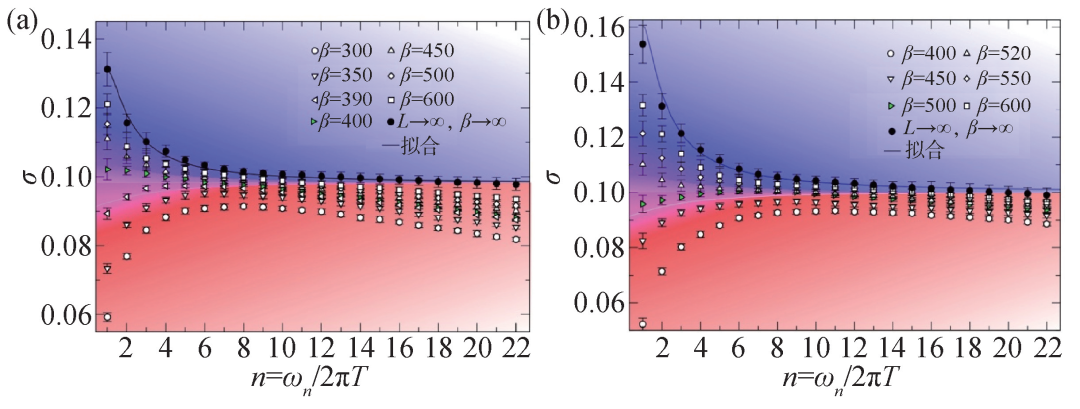 圖3 (a)不同温度(β=1/T )下,蒙特卡洛計算所得的玻色子電導關於松原頻率的變化σ (ωn)。在熱力學極限下,温度趨於零温時,從奇Z2 QSL到超流相的(2+1)d XY*量子相變點上,電導的平台值σXY*=0.098(9)。該值在統計誤差範圍內恰好是傳統(2+1)d XY相變點電導σXY =0.3554的1/4。此處的自對偶温度β *~ 400(T *~1/400);(b)類似的蒙特卡洛計算結果,對於從偶Z2 QSL到超流相的(2+1)d XY*量子相變點,1/4的分數化電導和自對偶温度也穩定存在
圖3 (a)不同温度(β=1/T )下,蒙特卡洛計算所得的玻色子電導關於松原頻率的變化σ (ωn)。在熱力學極限下,温度趨於零温時,從奇Z2 QSL到超流相的(2+1)d XY*量子相變點上,電導的平台值σXY*=0.098(9)。該值在統計誤差範圍內恰好是傳統(2+1)d XY相變點電導σXY =0.3554的1/4。此處的自對偶温度β *~ 400(T *~1/400);(b)類似的蒙特卡洛計算結果,對於從偶Z2 QSL到超流相的(2+1)d XY*量子相變點,1/4的分數化電導和自對偶温度也穩定存在
不過興趣就是最好的動力,科學的魅力總是招引着我們不斷往前追趕。在克服了諸多計算上的困難之後,我們看到如果把每個松原頻率上的電導值再做一步不同温度的外插,會得到系統在(2+1)d XY*相變點上的一條具有普適行為的電導隨着松原頻率的曲線,就是圖3(a),(b)中記為擬合的黑色實線。這兩條黑實線在中間頻率範圍明顯存在一個平台,這個平台所對應的電導,就是我們尋找的universal電導。而這個電導值,對於奇和偶Z2 QSL和(2+1)d XY*相變點來説,都是σXY*∼0.09,正好是前面提到的玻色子超流的(2+1)d XY相變點上σXY的1/4。這就是Z2量子自旋液體具有分數化電導的直接觀測結果,就像人們在分數量子霍爾效應實驗中觀測到的分數化電導一樣。以後人們再説起來Z2拓撲序量子自旋液體和其中的分數化任意子激發,除了大部人聽不懂的anomalous dimension指數,終於有了這個比較容易理解的分數化臨界電導[1]。
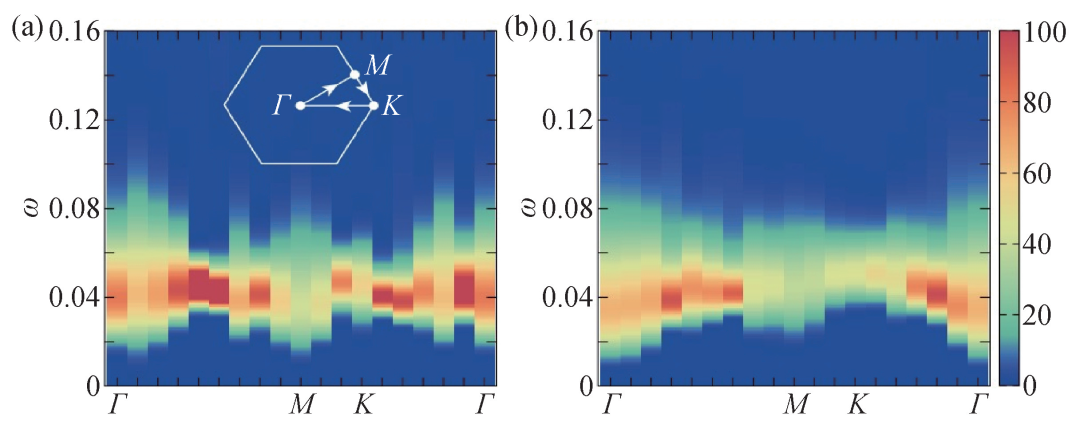 圖4 (a)在奇Z2量子自旋液體相中,通過蒙特卡洛計算得到的vison-pair譜函數,可以看到的確存在一個很小的能隙,其對應的温度尺度,暗合圖3中電導計算裏看到的自對偶温度T *;(b)類似的蒙特卡洛計算結果,對於偶Z2量子自旋液體相,亦如此
圖4 (a)在奇Z2量子自旋液體相中,通過蒙特卡洛計算得到的vison-pair譜函數,可以看到的確存在一個很小的能隙,其對應的温度尺度,暗合圖3中電導計算裏看到的自對偶温度T *;(b)類似的蒙特卡洛計算結果,對於偶Z2量子自旋液體相,亦如此
其實問題比我們想象的還更加有趣。1/4的universal電導是因為Z2自旋液體中的自旋子帶有正常玻色子一半的電荷。如果我們仔細看圖3(a),(b)中不同温度下的數據,可以發現,電導的數據在高温和低温的時候,還有一個湧現的自對偶行為 (self-duality)。大體上説,就是藍色背景 (低温) 和紅色背景 (高温) 的數據,關於粉色背景的區域上下對稱,而粉色背景區域的電導值,也就是我們上面提到的電導隨着温度外插後的universal平台值。這樣的自對偶行為,在傳統的玻色子超流(2+1)d XY相變點處計算中是不存在的[5,6]。我們認為這也是拓撲序量子自旋液體系統不平常的地方。這是因為在Z2 QSL中還存在另一種vison任意子激發,它不帶電荷,有一個比較小的能隙,乍一看不會對臨界電導造成影響。但是vison是可以與自旋子發生相互作用的,也就是可以散射自旋子。當温度很低時,就是圖3中的藍色背景區域,系統温度低於vison的能隙,自旋子與vison的散射不強烈,電導有一種表現形式;當温度較高時,就是圖3中的紅色背景區域,自旋子和vison激烈散射,電導就有了另一種表現形式。區分二者的中間温度,就是粉色的自對偶温度T*,大概就是vison的能隙所對應的温度尺度。Vison的能隙大小,或者説自對偶温度的大小,其實可以通過系統中另一種動力學測量給出 (就是自旋SzSz的能譜或者玻色子密度關聯的能譜),如圖4所示,可以清楚的看到,圖4(a),(b)所展示的vison-pair譜函數,不管對於奇還是偶的Z2 QSL,都有一個很小的能隙,能隙所對應的温度,都暗合圖3(a),(b)中電導曲線的粉色自對偶温度T*。
所以,浪蕩漢子們通過Z2量子自旋液體到超流的相變點上的電導測量,以分數電導的存在,揭示了系統存在自旋子任意子;又通過有限温度電導曲線的自對偶行為,揭示了系統中存在vison任意子,而且自旋子和vison也不像簡單模型中那樣沒有相互作用,而是存在着有趣的關聯和散射行為。拓撲序和湧現分數化激發所代表的超越朗道範式的量子物質形態,在這一個工作上都被我們清清楚楚地看到了。我們從中體會到的科學的美和有趣,通過筆者這些略顯笨拙的描述,也很勉力地希望能夠分享給大家。對於浪蕩漢子們來説,這些作品,就是對他們最好的鼓勵和回報,環境的變換和生活的磨礪,不會改變他們詼諧幽默的風格,在科學上的孜孜以求,還有朋友們之間的互助,“做自己認為有意思的事情,所有的事物和經歷都會成為滋養我們創造的養分”,就是讓他們繼續浪蕩下去,探索新的有趣的風景的動力。
對於略知前文引子部分故事來龍去脈的讀者諸君,再寫這樣一段話做結吧。“星斗其文,赤子其人”,這是懂藝術的人們對於沈從文的評價,放在黃永玉身上也是成立的。從湘西無愁河上走出來的浪蕩漢子們,無論環境如何嚴酷,無論生活甚至是生存的壓力如何鋪天蓋地的過來,他們都能學着用赤子之心化解成滋養自己做認為有意思的事情的養分,寫散文小説、刻木刻、畫畫、設計版畫、研究文物和考古等等都做出了了不起的成績,為民族、為世界留下了閃耀着人性趣味和光輝的財富。愛、憐憫、感恩,都是他們珍視的品質。希望我們的科學工作者隊伍裏面,也能多一些這樣的浪蕩漢子們,多一些這樣看破一切人事乘除,得失榮辱,全置度外,心地明淨無渣滓的人。
參考文獻
[1] Wang Y C,Cheng M,Krempa W W et al. Fractionalized conductivity and emergent self-duality near topological phase transitions. Nature Communications,2021,12:5347
[2] Wang Y C,Yan Z,Wang C J et al. Vestigial anyon condensation on kagome quantum spin liquids. Phys. Rev. B,2021,103:014408
[3] Wang Y C,Zhang X F,Pollmann F et al. Quantum spin liquid with even Ising gauge field structure on kagome lattice. Phys. Rev. Lett.,2018,121:057202
[4] Sun G Y,Wang Y C,Fang C et al. Dynamical signature of symmetry fractionalization in frustrated magnets. Phys. Rev. Lett.,2018,121:077201
[5] Katz E,Sachdev S,Sørensen E S et al. Conformal field theories at nonzero temperature:Operator product expansions,Monte Carlo,and holography. Phys. Rev.B,2014,90:245109
[6] Chen K,Liu L,Deng Y et al. Universal conductivity in a two-dimensional superfluid-toinsulator quantum critical system. Phys. Rev. Lett.,2014,112:030402
本文經授權轉載自微信公眾號“中國物理學會期刊網”。