吃着熱狗就把數學整明白了？_風聞

原創：中科院物理所

中國剩餘定理是關於最小公倍數的一個古老而強大的擴展。

如果你曾經為了户外燒烤而買過熱狗，你可能會發現自己正在解一道涉及最小公倍數的數學題。這裏涉及的問題是：為什麼通常一袋熱狗有 10 根，而一袋麪包卻只有 8 塊？這使得我們需要用數學的方法搭配熱狗和麪包的數量。

一個簡單的解決辦法是買 8 袋熱狗和 10 袋麪包，但誰會需要 80 根熱狗呢? 那麼，你能買更少的袋數，仍然使熱狗和麪包的數量相匹配嗎?

讓我們列出通過購買不同袋數而獲得每種物品的數量。

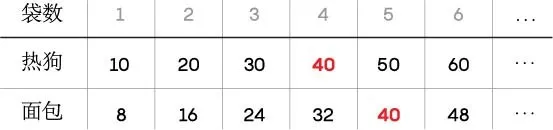
每個列表上都有一個 40 ，因為 40 是 10 和 8 的**最小公倍數(LCM)——它是能被這兩個數字整除的最小正整數。**如果你買 4 袋熱狗和 5 袋麪包， 40 根熱狗就會和 40 個麪包完美搭配。

但如果熱狗的包裝是一袋有 5 根（質數數量），而且 40 個熱狗超過了你的需求，那該怎麼辦?你還有比買 8 袋熱狗 5 袋麪包更簡單的方法嗎?下圖是新的列表。

在這種情況下，熱狗和麪包的數量達到 40 之前是不匹配的，因為 40 是 5 和 8 的最小公倍數。這是因為 5 和 8 “互質”——它們的公因數只有 1。**當兩個數互質時，最小公倍數就是它們的乘積。**當你開始列出8的倍數—— 8 × 1 ， 8 × 2 ， 8 × 3 ， 8 × 4 ， 8 × 5 ——你可以看到，除了 8 × 5 之外沒有其他 5 的倍數。

但是，當兩個數不是互質整數時，它們的公倍數有機會在達到兩者乘積之前匹配起來。

在第一個例子中，10 和 8 不是互質的，因為它們都有一個因子—— 2 ：

10 = 2 × 5，

8 = 2 × 4，

因為 8 已經能被 2 整除，所以你只需要找到一個 8 的倍數，讓它能被 5 整除，這個數就能被 10 整除。這就是為什麼最小公倍數為 8 × 5 = 40 ，而遠未達到 8 × 10 = 80 。

現在假設你去商店之前發現冰箱裏剩了一根熱狗，那麼你要再分別買多少袋熱狗和麪包來搭配?

這個新問題超越了簡單的最小公倍數問題，進入了更為複雜的中國剩餘定理領域。

中國剩餘定理最早是由中國數學家孫子在約2000年前提出的。中國剩餘定理存在於一個叫做模算術的數學領域，該領域通過分析數被其他數除後的餘數來研究數學，被用於從密碼學到天文學的多個領域。讓我們看看熱狗和最小公倍數如何幫助我們理解這個古老的算法。

如果你冰箱裏有一根熱狗，你可以在商店裏買每袋 5 根的熱狗，下面列出了你可以帶出去野餐的熱狗數量:

因為熱狗的數量總是 1 加上 5 的倍數，所有這些數除以 5 的餘數都是 1 。令 x 等於熱狗的數量，這個關係式可以寫成：

x ≡ 1 mod 5.

表述為“整數****x 與 1 對模 5 同餘”，意思是 x 除以 5 餘數為 1 。你也可以説“ x 同餘於 1 模 5 ”。

因為麪包的數量總是 8 的倍數，所以除以 8 的餘數總是 0 。如果 y 是熱狗麪包的數量，這個關係式可以寫成：

y ≡ 0 mod 8.

我們想要熱狗的數量和麪包的數量相等，所以要求 x = y ，為了找出什麼時候成立，我們可以解出下面的方程組：

x ≡ 1 mod 5x ≡ 0 mod 8

在一個方程組中，解一個同餘方程組的目標是同時滿足所有的同餘。

我們想要找到一個數 x ，當它除以 5 時餘數為 1 ，且當它除以 8 時餘數為 0 。如果能做到這一點，我們的熱狗和麪包就能完美搭配。

中國剩餘定理就是用來處理這類系統的。它告訴我們，只要兩個除數（也稱為模）是互質數，不管餘數是多少，就有一個大於或等於零但小於模乘積的唯一解。(如果兩個模不是互質的，則可能沒有答案。例如， x = 1 mod 6 和 x = 2 mod 8 的方程組沒有解，無論是小於 24 還是大於 24 。)因為 5 和 8 是互質整數，所以這個方程組應該有一個小於 40 的唯一解。

這個問題中的數字很小，所以我們可以通過列出熱狗和麪包的可能數量來找到答案：

如你所見，兩個表上都有小於 40 的數 16 ，這便是方程組的解。我們可以很快地檢查， 16 除以 5 的餘數是 1 、除以 8 的餘數是 0 。（注意，如果你把 40 ,也就是 5 和 8 的最小公倍數加上 16 ，你得到的 56 便是下一個方程組的解。）

中國剩餘定理不僅保證瞭解的存在，而且還給出了求解的方法。該算法依賴於這樣一個事實：如果兩個數互質，你總能找到它們的整數組合等於 1 。

讓我們看看這如何應用於另一個野餐問題。

想象一下，除了一個吃剩的熱狗，你還有兩個吃剩的麪包。現在你要買多少包熱狗和麪包才能匹配得上這些東西?

為了回答這個問題，我們需要解出以下的同餘方程組：

x ≡ 1 mod 5x ≡ 2 mod 8

為了找到由中國剩餘定理確定的解，我們將使用這樣一個事實：**因為 5 和 8 是互質數，它們的某個線性組合為 1 。**這句話的意思是，**我們可以找到整數 a 和 b ，使 5a + 8b = 1 。**你可以很容易地檢查 a = −3 和 b = 2 是否滿足：

5 × ( -3 ) + 8 × 2 = 1.

為了找到我們的解，中國剩餘定理的算法告訴我們，用5 × ( -3 ) 乘以麪包的餘數 2 ，用 8 × 2 乘以熱狗的餘數 1 ，然後把結果相加：

2 × 5 × ( -3 ) + 1 × 8 × 2 = -14.

就是説，我們最後可以吃到 −14 個熱狗和 −14 個麪包來進行匹配的熱狗麪包，這聽起來像一個關於數學家計劃野餐的垃圾笑話的笑點。但其實我們真正的解就藏在這裏。記住，我們知道 8 袋熱狗和 5 袋小麪包的值都是 40 （就像我們之前的例子中 16 和 56 的解一樣），所以我們只需要把 40 加 −14 得到 26 ， 26 便是大於 0 小於 40 的唯一解，而這便是由中國剩餘定理決定的。

你可以看到， 26 個熱狗和 26 個麪包解決了這個問題，如果你把每一個可能的數字列出來:

有一個簡單而巧妙的理由來解釋中國的餘數定理為什麼成立。要知道為什麼，想想所有小於 5 和 8 最小公倍數 40 的 5 的倍數：

這些倍數是 0 × 5 ， 1 × 5 ， 2 × 5 ， 3 × 5 ， … ，和 7 × 5 ，共有 8 個大於等於 0 但小於 40 的 5 的倍數。因為這些倍數都小於最小公倍數 40 ，所以當它們被 8 整除時，餘數肯定是不同的；如果其中任意兩個數除以 8 的餘數相同，那麼它們的差就能被 8 整除，兩個 5 的倍數之差也是 5 的倍數，於是這個差必然能被 5 和 8 同時整除，這樣就能被 40 整除。這是不可能的，因為小於 40 的兩個 5 的倍數不可能是 40 。

看看這裏所有不同的餘數：

因為除以 8 只有 8 個可能的餘數，所有可能的餘數都會出現在這個列表上。這意味着 5 在 40 以下的倍數包含了對 8 取餘的所有可能的餘數。換句話説，如果你冰箱裏剩下的麪包數量小於一袋，你就能做出少於 40 個熱狗。數學上用同餘方程組表述：

x ≡ 0 mod 5x ≡ a mod 8

對於任意 a ，解總是小於 40 ，只要檢查一下上面的餘數列表：對於 a = 1 ，解是 x = 25 ；對於 a = 2 ，解是 x = 10 ，以此類推。

如果你一開始多一個熱狗呢? 每當熱狗數增加 1 時，餘數增加 1 。但是因為所有的餘數同時被移動了 1，所以所有 8 個可能的餘數仍然可以被表示出來。

注意，餘數7向上移 1 等於 7 + 1 = 8 ，如果一個數除以 8 的餘數是 8 ，那麼它實際上是 8 的倍數，所以餘數實際上是 0 對 8 取餘。

這意味着同餘方程組：

x ≡ 1 mod 5x ≡ a mod 8

也有一個小於 40 的解，對於 a = 1 ，解是 x = 1 ；對於 a = 2 ，解是 x = 26 ，以此類推。

這個推理可以概括為：

x ≡ b mod 5x ≡ a mod 8

對於每一個 a 和 b 都有一個小於 40 的解，並進一步推廣以證明每個同餘方程組的形式：

x ≡ b mod mx ≡ a mod n

**只要 m 和 n 互質，**就存在一個小於 m × n 的解。這是中國剩餘定理最基本的內容。

這個定理和許多數論技巧一樣，在密碼學中很有用，密碼學是編碼和解碼秘密信息的數學。例如，你可以使用這個定理對一個數字加密，需要一組人共同合作來識別它。

假設你有一個想要保密的數字，在你的朋友張三和李四一起同意他們想知道這個數字後才能解密。首先給他們分配一對互質數——比如，張三和李四分別是 13 和 17 ——它們的乘積大於你的秘密數字。現在用你的數字除以他們每個人的數字，給他們每個人各自的餘數。他們各自都不會知道你的數字，但他們肯定能一起算出來，這要感謝中國剩餘定理！

假設你告訴張三的是 11 ，告訴李四的是 15 。這意味着張三知道你的數 x 滿足 x ≡ 11 mod 13 ,李四知道 x 滿足 x ≡ 15 mod 17 。這兩個方程單獨都不足以確定你的密碼，但它們一起構成了這個同餘方程組：

x ≡ 11 mod 13x ≡ 15 mod 17

而中國剩餘定理保證了該方程組有一個小於 13 × 17 = 221 的唯一解。張三和李四一起合作，就能算出你的號碼是 219 。

你可能不需要中國剩餘定理來計劃你的下一次野餐，但如果你需要在你的朋友之間分享信息或秘密地與你的將軍分享部隊數目，那你最好確保這個中國剩餘定理在你的計劃當中。