端着咖啡走路是一項鮮為人知的物理學壯舉_風聞

如何將一杯咖啡從咖啡機端到工位？

或者將一碗豆漿從餐廳窗口端到餐桌？

甚至是如何把一勺番茄蛋湯從鍋裏舀入碗內？

——乾飯人的每天靈魂拷問

撰文 | 蕉蕉的奇妙冒險

對於聰明的人類而言，這不過是生存的眾多基本技能之一。（手：這不有我就行？）

但對於物理學來説，端咖啡其實是一項了不起的壯舉！一切，都要從那兩隻擺鐘開始説起——

1 擺鐘之間的悄悄話

單擺是我們學習物理的過程中接觸的最早的模型之一。在單擺中，我們假設繩子一端固定，另一端連接一個質點，並假設繩子是沒有重量的，這樣所有的質量都集中一個沒有體積的質點上，對質點進行受力分析：該質點受兩個力的作用，一個是繩子的拉力，一個是重力，再加上繩子不可拉伸的約束條件，得到運動方程式為：

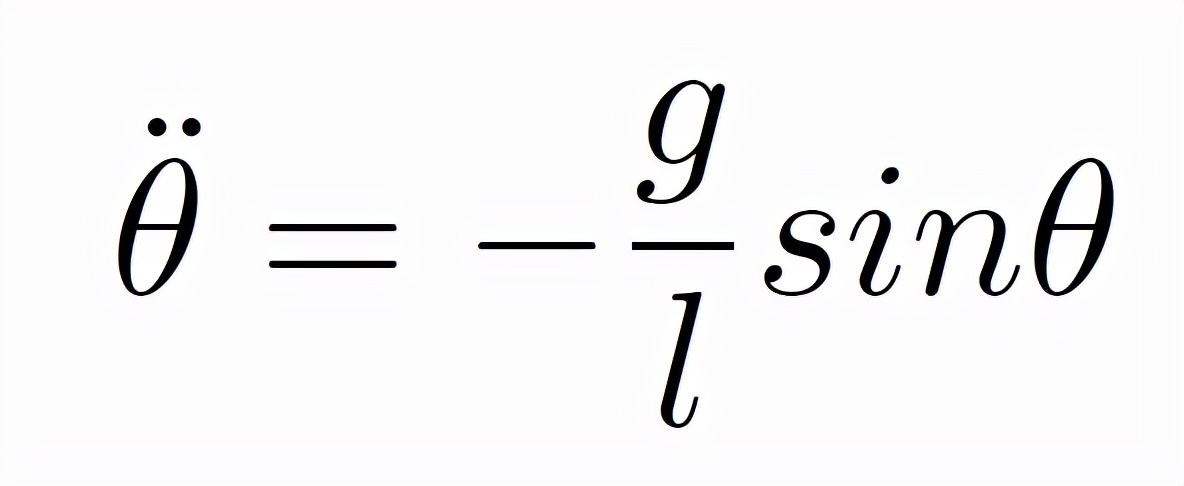因為sinθ的存在，這是一個非線性的常微分方程，在θ → 0 的情形下，我們可以做sinθ = θ的近似，這樣就將原來難以處理的非線性常微分方程，變成了易於處理的線性常微分方程。得到：

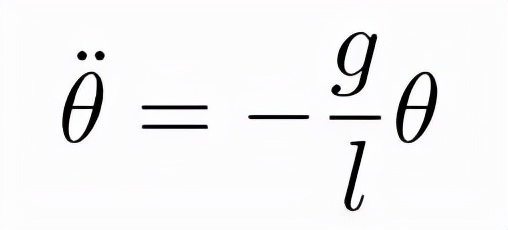它的解為：

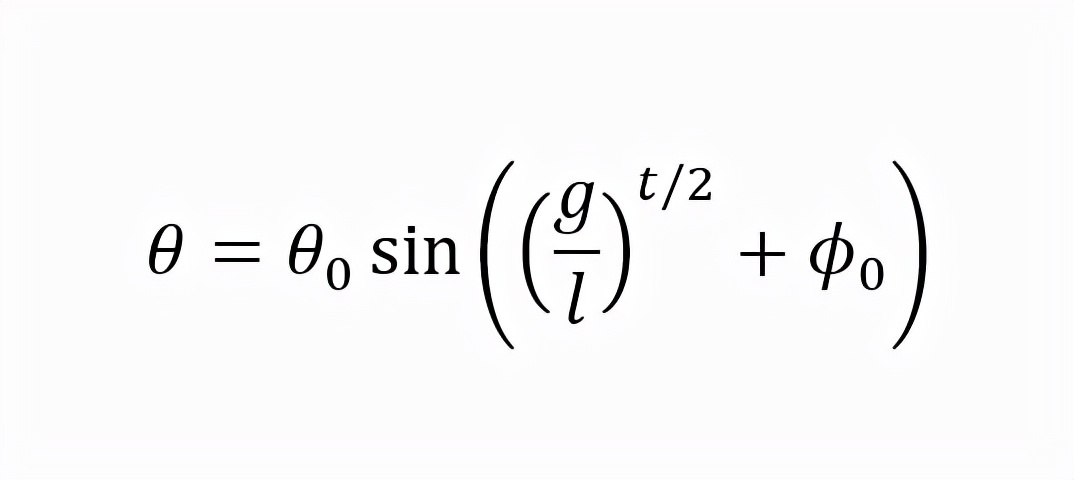其中θ₀，ϕ₀ 由單擺的初始狀態決定。這個解表明，單擺的角度正比於時間的正弦函數，這就意味着，單擺的運動具有固定的週期：

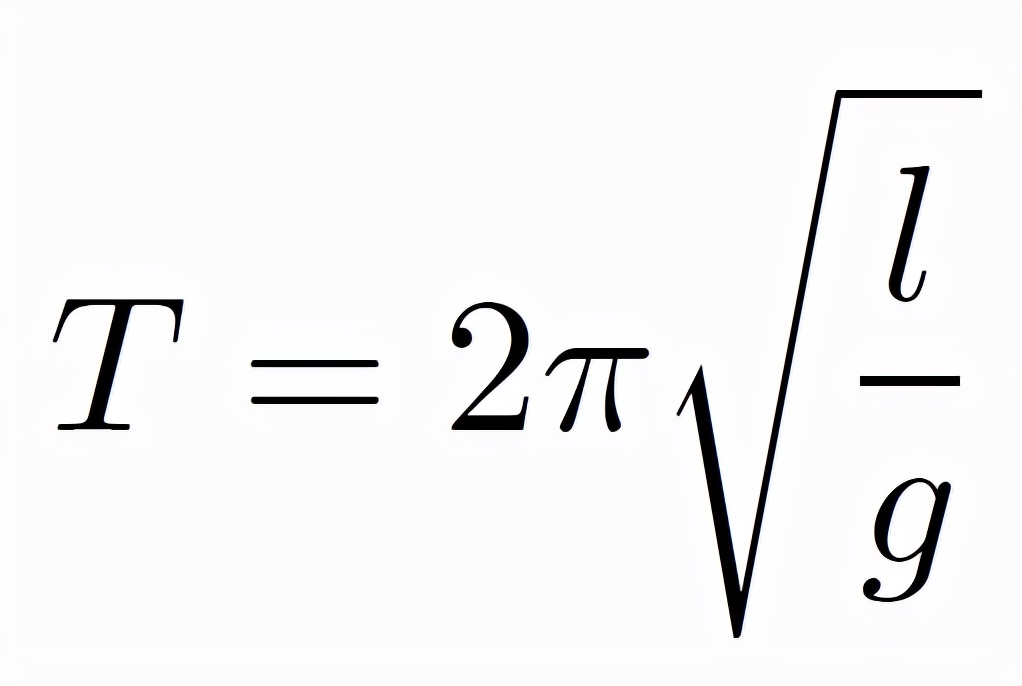並且這個週期只由該地的重力加速度和繩子長度決定，與單擺擺動幅度，單擺末端的質點的重量沒有關係。

依據這種特性，1656 年，荷蘭物理學家克里斯蒂安·惠更斯，發明了擺鐘，用於解決航海中測量經度時的需要。航海中，人們可以通過天文學觀測，確定所到之處的緯度；如果有準確的計時工具，就能根據一個經度已知的陸地參考點的時間，確定所到之處的經度。為了讓擺鐘計時更加地精確，惠更斯計劃在船上放兩個擺鐘。沒想到，兩個素不相識的擺鐘竟然……

……竟然擺着擺着，開始默契的同步了，就像説了什麼悄悄話一樣（雖然相位是完全相反的，即擺動的方向剛好相反）。丨來源：YouTube@Veritasium

也就是説，兩個放在一起的擺鐘，雖然擺錘初始的位置不同，各自原本的週期也不同，但經過一段時間的擺動，竟然變得週期相同了。這種現象的產生是因為，兩個擺不再是獨立的擺動，而是通過連接他們的物體發生了相互作用，直到擺動趨於一致。這種現象被稱為同步（synchronization）。

三個擺動雜亂的節拍器，通過與連接它們的複雜系統相互作用，最後擺動同步。丨來源：YouTube@Veritasium

2 當你端咖啡時，你在做什麼

當一個人端着咖啡，小心翼翼的行進時，他究竟對這杯咖啡做了什麼呢？

中學的物理圖像可能會説，人給咖啡杯提供了向上的支持力。但實際上，當看到自己的咖啡在杯子裏來回震盪，時刻伴隨着溢出的風險時，人們並不會無動於衷。（就像小時候每次看到這則《媽媽洗腳》公益廣告時，小編都會有億點點揪心——這得灑了多少水在地上啊……）

《媽媽，洗腳》的廣告中，小寶貝端的水灑了出去。丨來源：騰訊視頻

正如前面鐘擺所依靠的“第三方複雜系統”，端咖啡的人在咖啡與杯子之間也充當了這樣一個角色。此時，我們需要將杯子、咖啡和手的模型進行更加詳盡的刻畫。如果將杯子裏調皮的咖啡看成一個滾動的小球（如下圖（a）所示），那麼進一步在物理上，杯子與咖啡便可以抽象為“手推車”與“擺”的模型——這是因為，杯子裏小球總是貼着杯壁，其與杯壁圓弧所對應的圓心距離始終保持不變，相當於有一個不可伸長的繩子將其限制住（如下圖（b）所示）。我們可以將這個組合簡稱為“車-擺”模型。

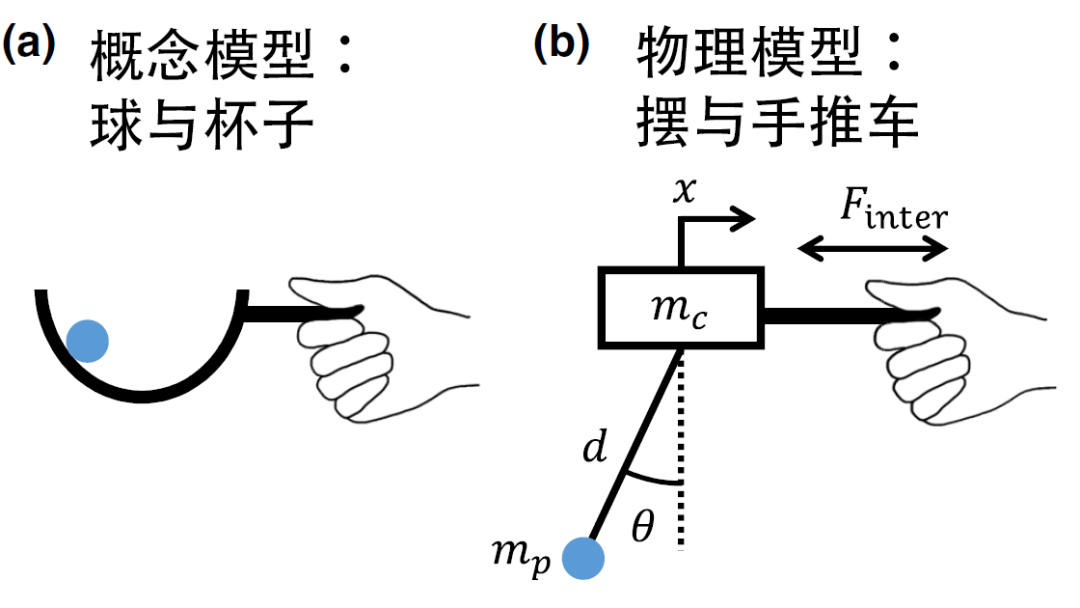端咖啡的概念模型與物理模型示意圖丨來源：文獻[1]

簡單來説，面對“想法不一致”的咖啡和杯子，人類的策略就是讓它們【同步】。

同步又分為兩種。一種是比較“激烈”的【反相同步】。當咖啡向右，趁其還未溢出時趕緊把杯子往左移；咖啡向左，就趕緊把杯子往右移。這樣，讓咖啡不停的在杯子裏來回震盪，只要你晃得夠快，咖啡就會被杯壁擋回來。這便是“高頻”的反相同步策略——咖啡震盪的相位和咖啡杯移動的相位總是相反。

對牆擊球時，手與球之間就是反相同步。手和牆=咖啡杯壁，球=咖啡丨來源：bilibili @東南排球訓練營

相反的，另一種【同相同步】則更加温柔。當咖啡要向右了，就讓杯子追隨咖啡的步伐，也向右移動——畢竟咖啡不會無限的向右移動（因為咖啡同時也向上移動，動能轉換為勢能而使速度降低），杯子移到一定的位置時咖啡也就停止向右的躁動了；當咖啡開始向左，故伎重演，讓杯子追上其向左的步伐便是，不必驚擾咖啡。在這種情況下，杯子移動的沒有那麼快，而移動的方向卻與咖啡始終保持一致，所以是“低頻”的同相同步策略。

湯姆端盤子時，身體和盤子就是同相同步。湯姆=咖啡杯，盤子=咖啡丨來源：youku@核桃話綜藝

反相高頻和同相低頻，還可以藉助擺長與頻率的關係進一步理解。在“車-擺”模型中，反相與同相分別如下圖（a）和（b）所示。由於車一直在移動，兩種同步運動的等效擺長不同。反相同步的等效擺長明顯小於同相同步的等效擺長，由上一節的頻率與擺長關係可知，擺長越短，週期越小，頻率越高。因此反相同步為高頻、同相同步為低頻。

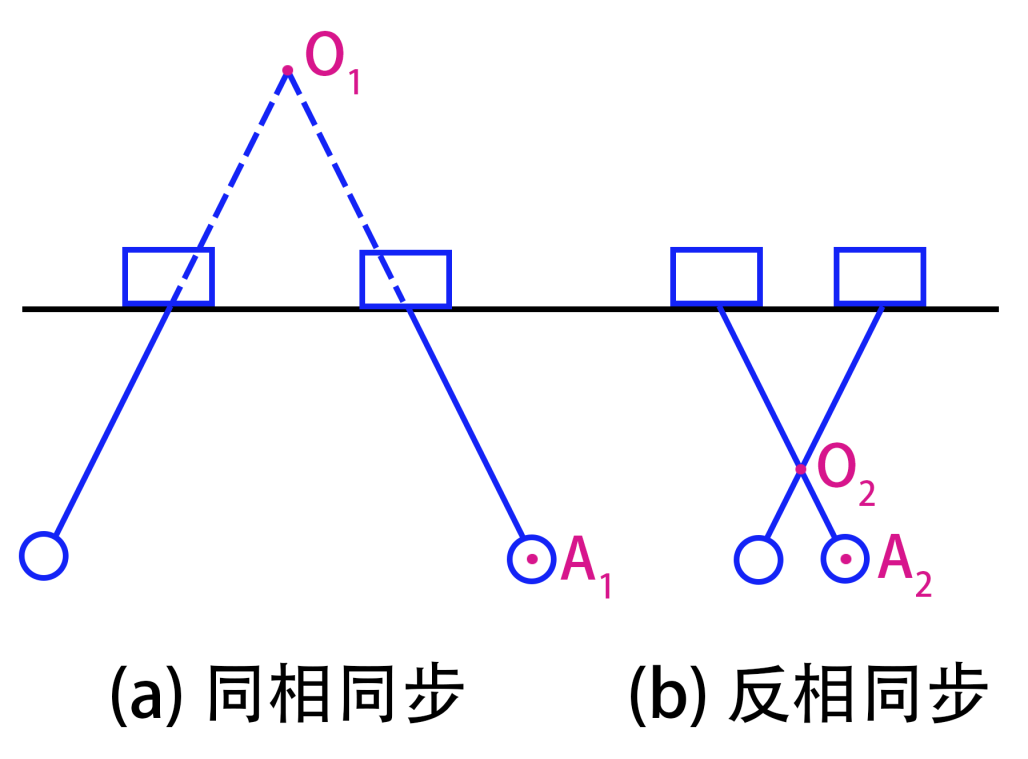兩種同步運動的等效擺長示意圖

實際上，聰明的人類很有可能在不自知的情況下，熟練的在兩種同步模式之間無縫切換——僅憑觀察力和直覺，便能在端咖啡挑戰中隨機應變。但是，如果要設計端咖啡的機器人，我們改如何賦予它這個看起來理所應當的技能呢？

針對端咖啡的兩種同步策略進行建模計算，研究者發現，同相與反相同步之間還存在一個【過渡區域】。這種過渡區域是由動力學系統的非線性所導致的。如果機器人被設計成以相對較小的步幅行走，將對應一個較小的週期外力，這時候動力學方程可以近似為線性，兩種同步運動間不存在過渡區域，因此行走的頻率可以是任意的；當機器人被設計成以較大的步幅行走時，對應較大的週期外力，這時候，在同相同步與反相同步之間存在一個不同步的過渡區，則行走的頻率應該儘量避開這個過渡區的頻率，以免咖啡與杯子發生不同步。

大步幅vs.小步幅丨來源：bilibili

3 無處不在的同步現象

除了端咖啡，同步現象無處不在：天空的飛鳥羣只能知道相鄰飛鳥的情況，卻最終能實現整個飛鳥羣整齊的飛行——

鳥羣的同步丨來源：YouTube@Veritasium

每隻螢火蟲都有自己獨有的發光頻率，而當螢火蟲的密度大到一定程度時，他們就會同步發光——

螢火蟲閃爍的同步丨來源：YouTube@robin meier

我們都聽説過軍隊在橋上齊步走，會因為與橋發生共振而導致危險。但是，沒有受過訓練的旅客在橋上也可能齊步走。這是因為，每當旅客邁出一步，就會讓給橋在側向有一個微弱的力，這個微弱的力造成的橋的運動狀態的改變又會影響其他旅客的腳步，於是旅客們的步伐通過橋相互影響，最終達成了同步。

2000年6月，泰晤士河上350米長的“千禧橋”出現明顯擺動。丨來源：YouTube@Veritasium

這些例子中每個個體都只能感受到自己附近的情況——這相對於整體來説很小；但卻能夠實現整體上的同步，這便意味着，整體不是部分的簡單加和。個體在組成整體時，因為相互作用的存在，會湧現出新的現象和規律，這些現象和規律是無法通過觀察個體發現的。這正是非線性的特點。我們都知道，在線性關係中，各變量間是互不相干的獨立關係，滿足疊加原理（整體等於部分之和）；而非線性關係則有相互作用，正是這種相互作用，使得整體不再是簡單地等於部分之和，還需要考慮各部分之間的耦合作用。當一個人端咖啡的時候，他便是咖啡與杯子耦合作用的來源。這也正是諾獎得主菲利普·沃倫·安德森所説的：量變引起質變（More is different）。

用線性的方式看待世界，可以讓事物變得更簡單——再大再複雜的系統，也可以分解為許多簡單個體的加和；但用非線性的方式看世界時，卻能讓事物變得更美妙——畢竟，每天一個小壯舉，誰不愛呢？

參考文獻

[1] Phys. Rev. Applied 16, 034012 (2021) - Synchronous Transition in Complex Object Control (aps.org)

[2] Walking with coffee is a little-understood feat of physics

[3] Predictability, force, and (anti)resonance in complex object control | Journal of Neurophysiology

[4] Stability and predictability in human control of complex objects: Chaos: An Interdisciplinary Journal of Nonlinear Science: Vol 28, No 10 (scitation.org)

[5] 非線性 百科 (quark.cn)

[6] The Surprising Secret of Synchronization - YouTube

[7] Fireflies in the Woods relaxation meditation Natural Sounds & Music - YouTube

本文經授權轉載自微信公眾號“中科院物理所”。特別鳴謝：平平無奇小葉榕；封圖背景來源：bilibili；表情包來源：網絡；編輯：蕉