數學魔法師康威的遊戲人生_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2021-12-19 10:19

撰文 | 倪憶
上帝是怎樣創造這個世界的?按照《聖經》的説法,第一天他在一片混沌中游蕩,發現太黑了,就説:“要有光”,然後就有了光……他總共花了六天來創造萬物,第七天休息。但並不是就此一勞永逸地結束了,麻煩事還在後頭,像什麼偷食禁果之類的。他得花更多的時間和精力來維護這個系統,有時不爽了還得格一下盤(大洪水),——當然格盤之前需要保存一下數據(諾亞方舟)。有次自己親自深入系統來查一下毒,還給弄掛掉了……
其實沒有這麼麻煩,上帝這樣的大智者,自然找得到最方便的辦法。他應該是在一張餐巾紙上隨手寫幾個公式作為定義這個世界的規則,然後製造一次大爆炸。接下來的事情就不用他管了,他只需端起一杯咖啡,在一旁悠然地看。
不信嗎?那麼就嘗試一下Game of Life吧。在一個有許多正方格的大棋盤上隨意放一些棋子,稱為胞體(cell),然後遵循下面的規則:
(i) 復生:一個胞體在t時刻是“死”,而在t+1時刻是“活”,如果它的八個鄰域有三個胞體在t時刻是“活”的。
(ii) 死於孤單:一個活的胞體在t時刻沒有或只有一個胞體鄰域,就會在t+1時刻死亡。
(iii) 死於過度擁擠:一個活的胞體在t時刻如有四個或四個以上的鄰居,就會在t+1時刻因過度擁擠而死去。
(iv) 生存之道:一個胞體在t時刻生存而能延續生命到t+1時刻,當且僅當它在t時刻有二個或三個活鄰域。
就是這樣簡單的規則,卻可以隨着初始狀態的不同產生無窮無盡的變化,有興趣的讀者可以連上https://playgameoflife.com/,隨意自己設定初始狀態,或者打開別人設計好的一些有趣的狀態,看看這個簡單平台上出現的複雜世界。
1970年,這個“生命遊戲”甫一發明出來便轟動了世界,很多人樂此不疲。據説有一段時間,全世界四分之一的電腦都在運行這個程序。這個遊戲的設計者,就是本文的主角,普林斯頓大學數學系教授,英國數學家John Horton Conway。

Lord of the Common Room
大約十年前的一篇訪問記中,説Conway每天打開計算機時,屏幕上會隨機顯示十個日期,比如1789年7月14日,2037年12月26日等等,Conway則心算出這些日期分別是星期幾,輸入後才能進入電腦。他的最高紀錄還不到20秒就算出了全部星期。(Conway的算法在《數學頑童的圓周率日》一文中有簡單介紹。)這種情形我倒是從沒見過,因為我見到的Conway一向都是使用common room(公共休息室)外的公用電腦。
Conway絕對是一個佔用公共資源的專家。系裏的common room就是他的辦公室,裏面的沙發寬大又舒適,足夠容納他的身軀。Common room內外有好幾塊黑板,剛好能讓他打草稿——按他自己的説法是:talk to myself on the blackboards. 桌子上堆着他的玩具。各種各樣的人都會到common room裏來,所以Conway從不缺乏聊天的對象。
有一次我正在common room裏喝咖啡,突然聽見電話鈴響。我正納悶,想誰會打電話到common room裏來呢,卻聽見電話機旁的一名學生大喊“John”,同時看見Conway一個箭步從聊天的人羣中竄了出去,拿起電話就是一聲hello……暴汗。後來見多了也就見怪不怪了,我甚至還替他接過一次電話。
我曾問過Conway,為什麼他喜歡呆在common room裏面,他説因為他自己的辦公室裏非常亂。據他説,最初系裏給他兩個辦公室,後來覺得兩個太多了,便收回了一個。(想當初必定是用兩個辦公室作為優惠條件來吸引他,如今新人勝舊人,就給減掉了,資本主義真是殘酷。)
他的辦公室在三樓,離common room只有幾步路,跟更高樓層裏的那些辦公室不是一個型號。這間面積相對小許多,門還是玻璃門。Conway在門上貼滿了數學畫報,不過想偷窺的人還是能透過縫隙看見裏面的情形,——也沒什麼好看的,反正我最初看到時還以為是系裏的雜物間。

下面這段描寫(by Richard Guy)能讓讀者對他辦公室裏的情形有個概念:
“他的劍橋大學純數學和統計系的辦公室裏幾張桌子堆滿了論文、書籍、沒有回覆的文件、筆記、模型、流程、圖表、幾個喝完沒洗的咖啡杯以及一些各種各樣的玩藝兒,這些東西氾濫到地板上和椅子上,因此很難容兩人在辦公室裏及坐下來。如果你能走到黑板,你會看到各種顏色的粉筆字跡,卻沒有地方讓你寫東西。雖然他有很好的記憶力,可是他常常找不到幾天前他寫下重要發現的紙張,他只好重新寫。”
Conway從來不看信,收到信件後便往故紙堆裏一扔。等他再發現這些信件時,看到上面的郵戳是幾年前的,就決定永遠不去拆閲,免得自己產生內疚感。不過他e-mail收得倒是非常勤,經常能看見他坐在common room外的公用電腦前,滿面笑容,飛快地打着字。
每天下午tea time時,Conway周圍就會聚集一些跟他關係好的教授或學生聽他胡侃。當然他的魅力還比不上點心,只要新的一盤點心端上來,這幫人便紛紛起身(common room裏的其他小羣體也是一樣),Conway還總是搶在頭裏。上學期他的一門課與tea time的開始時間重合,但他通常要晚十分鐘才去上課,因為點心一盤也不能少吃。有時他甚至一邊啃着點心一邊在黑板上奮筆疾書。上他課的幾個人在吃點心方面自然也都跟他臭味相投,對推遲幾分鐘毫不在意。
甜食帶來的一個壞處就是讓他的體形不能保持。其實在美國比Conway胖的人比比皆是,但數學家裏有他這麼大肚子的卻少見。對於他這個年紀的人,胖是一件很危險的事。去年期中的時候,Conway突然從common room裏消失了,後來才聽項武忠教授説他患心臟病動了手術。我當時很詫異,因為他看上去活蹦亂跳的。項武忠解釋説:“他太胖!”
手術後Conway恢復得很好,就是在家裏一天都呆不住,他太太為此寫信到系裏,請大家打電話或去家裏騷擾他。等再看見他時,已經臨近期末。那時他身體還沒完全好,一説話就喘不上氣,卻已經很着急地跑到common room裏找人聊天。聊天之餘又在黑板上寫寫畫畫,儘管都是些高中水平的數學。他説自己好長時間不做數學,得先做一些簡單的來恢復一下能力。
A Tale of Two Universities
英國制度,11歲入中學,這時就要根據未來的志願選擇學校。Conway説他在那時就決定去劍橋當一名數學家。他在Harold Davenport手下拿到博士學位後留校任教,研究數理邏輯。當時他感到非常沮喪,因為自己沒有拿得出手的成果,覺得不是在做真正的數學。
很快機會就來了。1965年,John Leech在研究裝球問題時發現了一種24維的格(lattice)。(Ernst Witt説他在1940年就發現了Leech lattice,但當時沒有發表。)他覺得這個lattice的自同構羣可能會很有趣,但自己的羣論水平不足以對其研究,便把這個問題告訴了許多羣論專家。只有Conway比較徹底地研究了這個羣,從其商羣和子羣中一舉發現了三個新的有限單羣。Conway從此聲名鵲起,被邀請到許多地方報告他的發現。他獨特的演講風格給人留下了深刻印象,而Conway也因此獲得了信心,邁入一流數學家的行列。

除了他發現的三個被稱為Conway羣的有限單羣,Conway在這一領域最著名的工作是他跟Simon Norton在1979年提出的魔羣月光猜想(monstrous moonshine)。這一猜想把最大的散在單羣“魔羣”的表示與模形式聯繫在一起,在1992年被Conway的學生Richard Borcherds證明。Borcherds因此獲得了1998年的菲爾茲獎。魔羣月光猜想及其推廣跟理論物理裏的弦理論有着奇妙的聯繫。它的證明用到了弦理論裏的成果,而這個猜想本身也對弦理論有許多反哺。例如Edward Witten用它來計算黑洞的Bekenstein-Hawking熵,得到的結果跟傳統方法算出來的非常接近。
我曾問Conway為什麼要把這個猜想命名為“月光”,他説moonshine這個詞在英語裏有illegal(違法)的意思。他們提出這一猜想時,大家還不知道魔羣是否存在,所以猜想其性質這件事是illegal的。(在另外的場合,Conway則解釋説moonshine有crazy(瘋狂)的意思,——這個猜想太瘋狂了。)
本質上説,Conway是一位組合學家。他研究的問題多數帶有組合特性,看起來非常淺顯,但其中卻藴藏着深刻的數學思想。就拿前面提到的生命遊戲來説。1940年,John von Neumann提出cellular automaton(元胞自動機),試圖建立一個數學模型來描述機器的自動複製與生長。Von Neumann最初的模型非常複雜,Conway將其簡化成人人都能理解的“生命遊戲”。生命遊戲經Martin Gardner在Scientific American上介紹後迅速風靡世界,Conway因此獲得了數學界以外的巨大聲名。(最近Mathematica的創始人Stephen Wolfram寫了一本書A New Kind of Science,把cellular automaton大肆鼓吹了一番,有興趣的讀者可以弄來讀讀。)
Conway説,他曾經認為自己是一流的數學家,可以做任何事,但現在他已經改變了自己的方向,只嘗試讓每件事物以最簡單的形式出現在每個人面前。前面所説的生命遊戲就具有這種特點。
Conway的另外一項出名的工作來自紐結(knot)理論。紐結理論是拓撲學的一個分支,但也可以用純粹的組合方法進行研究,這正是Conway的拿手好戲。
美國數學家James Alexander在1923年定義了一種紐結不變量,稱為Alexander多項式。Conway在六十年代發現了一個奇妙的拆接(crossing change)關係式,可以用來遞歸地定義Alexander多項式,連中學生都能看得懂,計算起來也很方便。(拆接關係式在Alexander的原始論文中已經出現,但沒有引起人們的注意。Conway實際上是重新發現了這一關係,並強調了其重要性。)

到80年代時,Vaughan Jones發現了一個新的紐結不變量:Jones多項式,並因此獲得1990年的菲爾茲獎。(Jones多項式發現過程中的故事可見《出名要趁早?94歲的新科女院士,41歲才獲得博士學位》。)Jones多項式滿足跟Alexander多項式非常相近的拆接關係式,而它們還可以推廣為更一般的HOMFLY多項式,滿足更一般的拆接關係式。
HOMFLY這個名字是發現它的六位數學家姓名首字母的組合。説起這事來Conway還頗有些耿耿於懷。他説當時自己好長時間沒有研究紐結,也不去參加各種會議。Jones多項式出現後他的那些紐結界的朋友們(比如説L)一直沒告訴他,瞞了他好幾個星期,等到HOMFLY多項式出來以後他才得到消息。他只用了一個下午就證明了這個HOMFLY多項式確實是紐結不變量,但為時已晚。Conway説如果他早知道Jones多項式的事,HOMFLY前面就得加個C成為CHOMFLY了……(當時還有兩位波蘭數學家P和T也獨立發現了HOMFLY多項式,但西方對他們工作了解較晚。文獻中也經常把這一多項式稱為HOMFLY-PT多項式。)
Conway於90年代初離開劍橋大學,來到普林斯頓做訪問教授。按普林斯頓的慣例,從別處挖人來時,給的是終身職位,但第一年的頭銜還是訪問教授,這樣如果一年過後這人不願意留下,還可以回原來的學校。Conway解釋説當初並不是他自己作決定留下來,“I was undecided”,是他的太太喜歡這裏。
Conway結過三次婚,跟第一位太太生了四個女兒,跟第二位有兩個兒子,跟第三位又生了個兒子。去年底他大病初癒時,我看見他帶着一個蹣跚學步的小男孩玩,便問他:“Is he your grandson?” 他自豪地回答:“No, he is my son.” 再問其年齡,答曰兩年三個月。我頓時肅然起敬,——要知道Conway可是1937年出生的。在我聽説過的數學家裏面,恐怕只有I. M. Gelfand在這方面比Conway更出色。
也許鼓勵創新的美國比相對保守的英國更適合Conway,儘管Conway堅持認為普林斯頓比劍橋更保守。美國人崇拜的科學英雄倒未必需要有非常出色的學術成就,但一定得有張揚的個性。Conway剛好就是他們所需要的類型,加之他又喜歡跟媒體打交道,所以Conway頻頻在媒體上曝光,聲名一時無兩。普林斯頓數學系三樓走道旁有一塊板,上面貼了各種關於系裏教授報道的剪報。Conway的報道佔了將近一半,跟John Nash不相上下。當然如今在好萊塢的炒作之下,Nash是比Conway出名多了。
另外一位著名的John Conway是以好幾本分析教材聞名於世的John B. Conway. 我起初還以為這兩位是同一個人,曾頗奇怪了一陣,因為John B. Conway寫的那些書跟John H. Conway的工作風格完全不同。後來才注意到兩者的中名不同。
我們的這位John Horton Conway説他曾經多次在會議上碰見過John B. Conway. 有一次參加一個會議,John H. Conway正低頭算些東西,突然聽前面有人問:“Are you the John Conway?” Conway頭也不抬地答道:“I don’t know, it depends on which John Conway you mean.” 一抬頭,發現就是另外那位John Conway。
John’s Adventures in Wonderland
Conway有種種奇奇怪怪的數學玩具,common room裏就堆着好多。上學期我選他的一門課,第一次課前見他在common room裏抱着一個箱子。看那個箱子的體積、形狀、質地,怎麼看都覺得裏面裝的是筆記本電腦。接下來他帶着箱子進教室,打開,原來是一箱積木,汗

他這次課講的是三維空間中對稱的分類,採用一套他自己創造的記號,——Conway研究問題時總喜歡使用自己的記號。我當時聽不太懂他的英國口音,只能狂抄筆記,他的板書中有好多即興發揮的縮略語,字跡又潦草,得費好大的勁兒來辨認。所以只忙着抄,根本顧不上思考其中的含義。
講課中間,Conway給每人發了兩個積木,叫大家説出積木的對稱性,——當然是用他自己的記號。另外兩個學生説對了,我卻都錯了。Conway勃然大怒,到黑板上把某個定義中的一句重念一遍,中間一個詞突然用十倍的音量吼出來“NOT!!!”,當時把我嚇得渾身一哆嗦。後來知道 Conway上課時獅子吼是常事,有位師姐也碰見過。還有一次我路過一間教室,忽然聽裏面傳出一聲咆哮“ABSOLUTELY!!!”,心知就是Conway在裏面上微積分課,正嚇唬本科小孩們。
前面已經説過,Conway是一流的紐結專家。別人講紐結都是用繩子、皮帶之類的有一定韌性的東西來演示,他偏要用剛性的東西。他有幾根彎曲的金屬管,連接起來後在接口處可以轉動,Conway能以此展示出所有交叉點不超過五個的紐結。有一次他在common room裏給大家擺弄這件寶貝,末了覺得不過癮,便往地下瞅。我被他瞅得心中直發毛,突然見他俯下身,伸出魔爪,一把握住我的鞋。我沒敢抵抗,任憑他把我的鞋連同腿腳一同擱到茶几上。然後他便開始解我的鞋帶,扯了幾下後發現我的鞋帶並不像他想象中那樣好解,於是又開始打別人的主意。環視一圈後沒找到合適的目標,只得轉而尋求更加正統的方法。他拿起筆,在一張紙上隨手畫了一些紐結,用的還是他自己的記號。不過畫紐結並非Conway的獨門絕學,好多紐結專家信筆一揮也能畫出非常複雜的紐結。
Conway還有許多數學內容的T恤衫,整天穿着。有些上面是數學漫畫,有的則相對簡單,比如圓周率到小數點後一千位。據説有一次Conway的太太需要用π的精確數字,便問Conway,Conway隨口就背出了小數點後的一百位。可他太太嫌不夠,問他能不能背更多。Conway感到很沒面子,便決定背到一千位。他制定計劃,每天跟太太出去散步時背上二十位,而且是兩人一起比賽着背,互相考問。這樣沒用多長時間,他們夫婦倆就都能背到一千位了。
Conway非常熱衷於研究有趣的初等數學,下面這個look-and-say序列就是一例,他在common room裏給我講過:
1, 11, 21, 1211, 111221, 312211, 13112221, …
這裏面有什麼規律呢?説穿了非常低幼。第二個數字11應該讀作“1個1”,表示前一個數字是1個1。第三個數字21應該讀作“2個1”,表示前一個數字是2個1連寫在一起。第四個數字1211應該讀作“1個2再1個1”,表示前一個數字先是1個2,再是1個1。第五個數字111221表示前一個數字先是1個1,然後是1個2,再是2個1……
這看起來就是幼兒園小朋友胡亂作的規定,Conway卻能發現其中的數學內容,專門寫了一篇論文研究其性質。比如説Conway證明了這個序列中出現的數字都由1, 2, 3組成。換句話説,只要你會數到3就能把這個序列一直寫下去。作為普林斯頓大學數學系的講席教授,Conway絲毫不覺得研究這種初等數學有多麼“跌份”。這或許是他有如此高人氣的一個原因吧。Conway是數學遊戲愛好者,他發明過好多遊戲,生命遊戲只是其中最有名的一個。據説以前在劍橋時,他經常在休息室裏赤着腳,用紙和筆來玩數學遊戲。有時他抓着學生、同事和訪客陪他玩,找不到對手就自己坐在地下研究這些遊戲。

下面這個“豆芽遊戲”就是Conway在劍橋時和Michael S. Paterson一起發明的。兩個人用紙和筆就可以玩,幼兒園小朋友也能理解。
遊戲開始時,在紙上畫若干個點。每方每回合在兩點(可以是同一點)間畫上一條連接線,然後在此線中間增加一個點,把這一條線分成兩條。連接線可以是直線或曲線,但不能跟自己或別的線相交。每一點最多跟三條線相連。
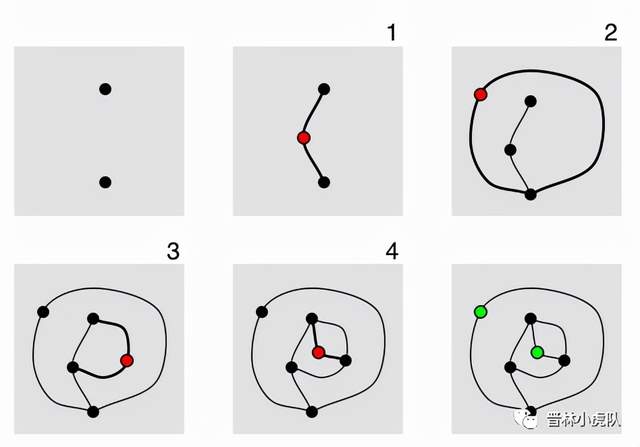
豆芽遊戲有兩個版本。普通版本(normal play)裏,畫最後一條線者贏;悲慘版本(misère play)裏則是畫最後一條線者輸。悲慘版本的難度比普通版本要大許多,有興趣的讀者不妨都試試。
Conway在遊戲方面的一個有趣結果是“超現實數(surreal numbers)”。他發現每個實數都能對應一個遊戲,相應地,實數的四則運算可以用遊戲的語言來解釋;此外還有許多遊戲具有類似於實數的性質,卻不對應實數。這樣,Conway便把遊戲看作“數”,得到實數體系的擴充,稱為“超現實數”。
Conway把他的想法告訴了計算機科學家Donald Erwin Knuth(高德納),Knuth對此大感興趣,便借自己在挪威度假的機會,寫成了一本小説體的數學書 Surreal numbers : how two ex-students turned on to pure mathematics and found total happiness : a mathematical novelette.
需要指出的一點是,Conway對遊戲的研究並非博弈論(Game theory)的主流,標準的博弈論教科書上根本沒有一點兒對Conway工作的介紹。Conway研究的遊戲確實非常有趣,但在我們這些人眼中,不會給數學帶來多大的進益。
也許在Conway看來,一個問題並不必重要或困難,只需要有趣便可以吸引他去研究。在21世紀的今天,數學已經更多地成為一種職業而非興趣。可對於如孩童一般在海灘拾貝的Conway來説,它永遠還只是遊戲。
參考文獻
[1] 勞拉·常,趙伯煒等譯,約翰·H·康威——神秘數學世界的漫遊者,《紐約時報50位科學家》,海南出版社,2003.
[2] 李學數,英國的怪數學家康威,《數學和數學家的故事3》,新華出版社,1999.
[3] J. J. O’Connor and E. F. Robertson, John Horton Conway, http://www-history.mcs.st-and.ac.uk/history/Mathematicians/Conway.html.
本文經授權轉載自微信公眾號“普林小虎隊”,原題目為《Conway:遊戲人生》。