理解黎曼猜想（五）跟外星文明交流，第一條信息應該發什麼？ | 科技袁人_風聞

導讀

無論任何行星，任何星系，甚至任何維度，數學的規律都不會變。想想看，除了質數之外，還有什麼更適合作為跟外星文明交流的第一條信息呢？質數跟我們經常強調的可控核聚變一樣，都是宇宙級別的關鍵科技！在這個意義上，可以把黎曼猜想理解為宇宙的密碼！

本文為黎曼猜想系列之四，

黎曼猜想（一）見黎曼猜想（一）每出現一個數學公式，就會嚇跑一半觀眾？如何打破“跳蚤效應” | 科技袁人，

黎曼猜想（二）見黎曼猜想（二）兩個自然數互質的概率是多少？我不僅算起黎曼猜想，還寫了個程序 | 科技袁人，

黎曼猜想（三）見黎曼猜想（三）你真的相信全體自然數的和等於-1/12嗎？| 科技袁人

黎曼猜想（四）見黎曼猜想（四）短短8頁紙，至今仍在給數學家啓發和挑戰，黎曼究竟寫了什麼？| 科技袁人

視頻鏈接：

西瓜視頻：

https://www.ixigua.com/7039529556599898657

本視頻發佈於2021年12月9****日，觀看量已超4萬

精彩呈現：

在上一期節目中，我們知道了一個根本性的結論：質數分佈的全部信息，都包含在黎曼ζ函數非平凡零點的位置之中。然後，我們介紹了黎曼猜想的內容。它説的是：黎曼ζ函數所有的非平凡零點，實部都等於1/2。

數學家經常把黎曼ζ函數非平凡零點的實部和虛部分別寫成σ和t，把複平面上0 < σ < 1的豎直條帶稱為臨界帶，把σ = 1/2的豎線稱為臨界線。我們已經知道的是，黎曼ζ函數所有的非平凡零點都位於臨界帶內部。而黎曼猜想説的就是，黎曼ζ函數所有的非平凡零點都位於臨界線上，在臨界線外一個都沒有。

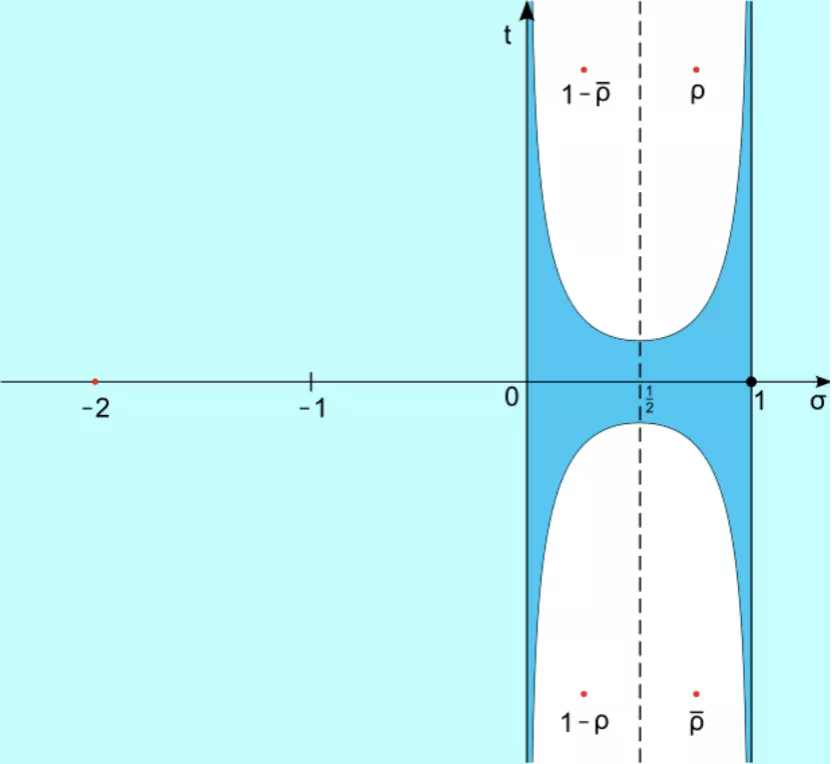
 臨界線與臨界帶

在繼續介紹之前，讓我們來回答一個許多人問起的問題：質數有什麼用？

我欣慰地看到，不少同學們都主動地做出了回答：質數在密碼學中有十分重要的應用。例如當今世界最常用的密碼體系之一叫做RSA，這個名字是三位發明者的姓的首字母縮寫。RSA密碼體系的基礎就是因數分解的困難性，即把一個很大的合數分解成兩個質數的乘積需要非常大的計算量。同學們的這種主動精神非常好！

我還可以補充一點質數在機械方面的應用：齒輪的齒數經常被設計成質數。為什麼呢？因為這樣可以使兩個齒輪的兩個齒在兩次相遇之間的齧合次數最大化，使磨損均勻化，增加耐用度，減少故障。

《三體》英文版封面

質數在日常生活中的應用固然很有趣，不過我還想再談一個宇宙層面的應用，就是作為智慧的標誌。在《三體》的第三部《死神永生》中，人類的太空艇探險隊和四維空間的文明進行了這樣的交流：

“按照計劃，卓文用中頻電波發送了一個問候語。這是一幅簡單的點陣圖，圖中由六行不同數量的點組成了一個質數數列：2、3、5、7、11、13。

他們沒有指望得到應答，但應答立刻出現了，速度之快讓三人不敢相信自己的眼睛。懸浮在太空艇艙裏的信息窗口顯示出一個簡單點陣圖，與他們發送的類似，也用六行點組成六個質數，但圖中的點陣大了許多，把他們發送的那個數列接了下來：17、19、23、29、31、37。

對方的含義很明確，回答了他們的問候。”

這在科幻小説中，是很標準的設定。無論任何行星，任何星系，甚至任何維度，數學的規律都不會變。而在數學中又屬自然數最為簡單，而在自然數中又屬質數最容易表現出智慧含量。想想看，除了質數之外，還有什麼更適合作為跟外星文明交流的第一條信息呢？

心事浩茫連廣宇，於無聲處聽驚雷。質數跟我們經常強調的可控核聚變一樣，都是宇宙級別的關鍵科技！在這個意義上，可以把黎曼猜想理解為宇宙的密碼！

上次我們説到，黎曼對小於等於x的質數個數即質數計數函數π(x)，推出了下面的表達式，其中唯一未知的就是那些非平凡零點的位置ρ：

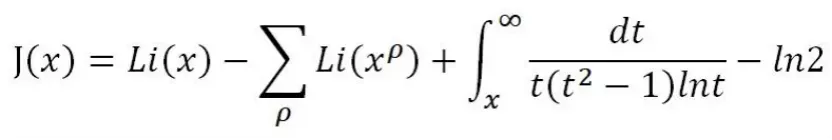
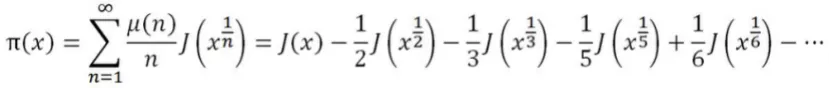
1896年，在1859年提出黎曼猜想的37年之後，阿達馬和德·拉·瓦·布桑證明了質數定理，並因此續到了90多歲。質數定理説的是，質數計數函數π(x)約等於對數積分函數Li(x)，也約等於x/lnx。

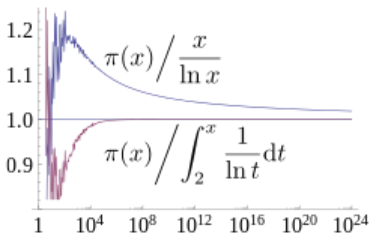
質數定理的相對偏差

因此，我們對質數的分佈可以這樣理解：質數定理給出了π(x)的基本輪廓，即Li(x)，黎曼ζ函數的非平凡零點給出了π(x)對這個輪廓的修正。而對於這個修正，黎曼猜想又給出了它的最重要的特徵。

什麼樣的特徵呢？我們可以注意到，對於一個複數ρ = σ + it，x的ρ次方的絕對值是由ρ的實部也就是σ決定的，因為ρ的虛部也就是t隻影響x的ρ次方的方向，而不影響其大小。我們還可以注意到，在x很大時，對數積分函數Li(x)約等於x/lnx，而lnx的增長速度比x慢得多，因此Li(x)的增長速度大約就是x。因此，如果黎曼猜想成立，也就是説所有的σ都等於1/2，那麼所有這些Li(xρ)加起來的增長速度就大約是x的1/2次方，即根號x。

你也許會問，無窮多個根號x加起來，難道不會發散嗎？回答是，別忘了ρ還有虛部呢，它會使x的ρ次方的矢量旋轉。因此不同零點的貢獻會在很大程度上抵消，最後得到一個有限的值，而這個有限值的長度正比於根號x。

如果黎曼猜想不成立，也就是説有些σ不等於1/2，會產生什麼後果呢？如果有一個非平凡零點的σ > 1/2，也就是説它位於臨界線右側，那麼它就會導致Li(xρ)的增長速度超過根號x。當x無限增大時，這一個零點的貢獻就會淹沒所有的臨界線上的零點的貢獻。好比你跟一羣人賽跑，你的速度是x的2/3次方，他們的速度是x的1/2次方，那麼當x充分大的時候，必然會導致他們跑過的路程加起來都沒有你多。因此，這一個右側的零點就會使得π(x)對Li(x)的偏離的增長速度超過根號x。

而如果有一個非平凡零點的σ < 1/2，也就是説位於臨界線的左側呢？別忘了，非平凡零點對於臨界線是對稱的。所以如果有一個在左側，就必然會有一個相應的在右側。因此，只要有一個非平凡零點不在臨界線上，就會導致π(x)對Li(x)的偏離的增長速度超過根號x！我們強調一下：只要有一個非平凡零點不在臨界線上，就足以導致可觀的後果了！

因此黎曼猜想意味着，在質數分佈對其輪廓所有可能的偏離中，實際取到的是最小的偏離。這是一個多麼深刻的猜測！現在你明白黎曼猜想的意義何在了吧？

例如美國數學家舍恩菲爾德（Lowell Schoenfeld，1920 - 2002）在1976年證明了，如果黎曼猜想成立，那麼下列不等式對任何大於等於2657的x都成立：

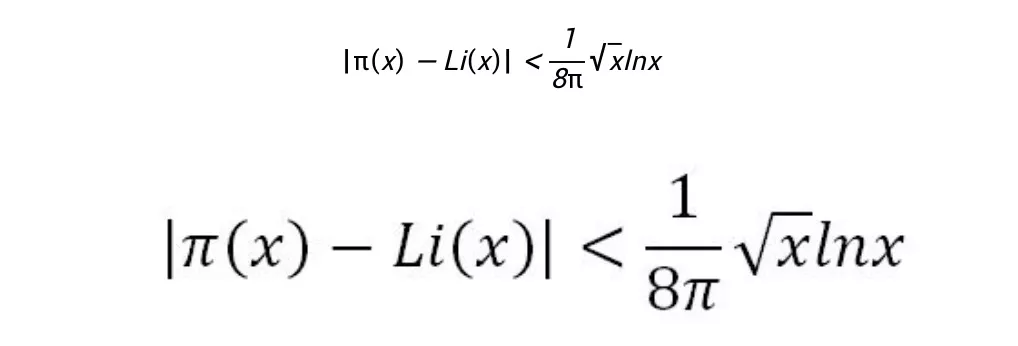
而如果不以黎曼猜想作為前提，那麼我們對|π(x) - Li(x)|的增長速度能夠證明的，就只是它不超過x。這跟黎曼猜想對應的結果根號x相比，就差得太多了！

人們已經發現了許多跟黎曼猜想等價的猜想。例如1984年，有一位法國數學家Guy Robin就證明了一個。這位法國數學家的姓Robin用英語讀出來像“羅賓”，但用法語讀出來更像“猴棒”，猴賽雷的猴，金箍棒的棒，真是太棒了。根據名從主人的原則，我們還是稱呼他“猴棒”吧。總之，猴棒證明了，黎曼猜想等價於下列不等式對任何大於等於5041的自然數n都成立： 

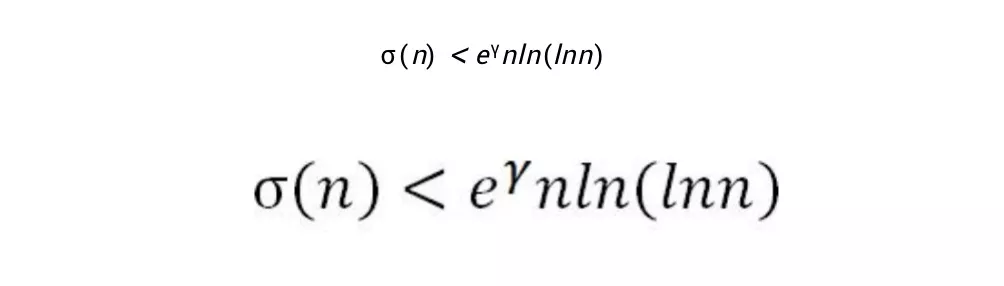
這裏的γ是歐拉常數，我們在本系列的第二篇中介紹過，約等於0.577216。而σ(n)是因數和函數（sum-of-divisors function），意思是一個自然數n的所有因數之和，包括1和這個自然數本身在內。例如12的因數包括1、2、3、4、6、12，σ(12)就等於1 + 2 + 3+ 4 + 6 + 12 = 28。

受到黎曼猜想的啓發，人們在數學的若干其他領域也提出了類似的猜想。這些猜想都可以理解為黎曼猜想的推廣，這些推廣也對數學產生了深遠的影響。

我的朋友盧昌海博士寫了一本非常好的科普著作《黎曼猜想漫談》（清華大學出版社2012年8月第一版），得到了許多圖書獎。著名的數學家、前中國數學會理事長王元院士給此書撰寫了序言，向大眾推薦此書。王元院士寫道：

“就像研究FLT（按：Fermat’s last theorem，費馬最後定理）與GC（按：Goldbach’s conjecture，哥德巴赫猜想）一樣，研究它們的目的主要在於發展數學中的新思想與新方法。形象地説，這兩個問題都是數學中的‘下金蛋的母雞’。

從過去的研究來看，RH（按：Riemann hypothesis，黎曼猜想）當然是數學中下金蛋的母雞，但研究它的目的，遠遠不止此。它之所以成為數學中第一重要問題，主要是由於一系列的數學中的重大問題的解決都依賴於各種RH的解決。一旦這些RH解決了，人類就站在一個不知比現在高多少的數學平台上，看到更遠得多的風景。”

《黎曼猜想漫談》

請看，王元對黎曼猜想的評價是，“數學中第一重要問題”！如果我們保守一點，那麼説黎曼猜想是“數學中最重要的問題之一”，則是完全沒有疑問的。

王元院士

黎曼猜想在公眾中的知名度，在很大程度上來自兩次世紀之交時的宣傳。

第一次是在1900年，偉大的德國數學家希爾伯特（David Hilbert，1862 - 1943）在國際數學家大會上提出了經典的23個數學問題，對後世產生了深遠的影響。其中第八個問題就是“黎曼猜想與其他質數問題，包括哥德巴赫猜想和孿生質數猜想”。事實證明這三個猜想都是特別難的問題，直到現在都沒有解決。

希爾伯特

第二次是在2000年，克雷數學研究所（Clay Mathematics Institute）提出了七個“千年大獎問題”（Millennium Prize Problems），對每一個問題的解決懸賞一百萬美元。其中第四個問題就是黎曼猜想。人們笑談，這是世界上最難的獲得一百萬美元的方法！

克雷數學研究所的這七筆懸賞發出去了幾筆呢？回答是：一筆都沒發出去。到目前為止，這七個問題中只有一個被解決了，就是第三個問題“龐加萊猜想”（Poincaré conjecture）。但是，解決者俄羅斯數學家佩雷爾曼（Grigori Yakovlevich Perelman）不屑於去領獎！這位長得有點像沙僧的哥們是個神人，以後我們有機會再來介紹他。

佩雷爾曼

雖然有這麼兩次大規模的宣傳，不過論起在公眾中的知名度，黎曼猜想還是顯著的落在哥德巴赫猜想與孿生質數猜想後面。這是因為後兩者的表述非常簡單，小學生都能看懂，而黎曼猜想的表述就複雜得多，需要有複變函數的知識才能理解。簡單地説，哥德巴赫猜想和孿生質數猜想很容易“扮豬吃老虎”，而黎曼猜想一看就知道是老虎。這倒也未嘗不是一件好事，至少號稱自己攻克了黎曼猜想的民科，就比號稱自己攻克了哥德巴赫猜想或者孿生質數猜想的民科少得多！

但如果論起在數學上的重要性，順序就反過來了。從王元的序言，我們可以理解，不少著名猜想的重要性主要在於啓發新思想，本身的用處比較小。而黎曼猜想不但能啓發新思想，而且本身的用處就非常大。因此，黎曼猜想雖然與哥德巴赫猜想、孿生質數猜想同列於希爾伯特第八問題，但重要性還是比它們高一個層次。

當然，我們並不是説哥德巴赫猜想與孿生質數猜想不重要，也不是説陳景潤與張益唐的工作不重要。哥德巴赫猜想與孿生質數猜想都是非常重要的問題，而且它們挑戰人類智力的時間比黎曼猜想還要長。陳景潤與張益唐的相關工作都是非常傑出的成果，值得我們高度的敬佩與讚譽。我們只是希望讀者明白，這些不是數學的全部，世界上還有其他的而且是更重要的問題需要關注。

對於專業數學家來説，他們都十分清楚黎曼猜想的重要性。例如有人曾經問希爾伯特，如果他能在500年後重返人間，他最想問的問題是什麼？希爾伯特回答説，他最想問的就是：是否有人解決了黎曼猜想？

來，讓我們為希爾伯特獻上一首《向天再借五百年》！

《向天再借五百年》

這裏有一點值得提的是，許多人在知道了密碼學和黎曼猜想都與質數有關之後，認為如果黎曼猜想被證明了，許多密碼體系就會被破解。我們必須指出，這是一種過度解讀。

實際上，從來沒有哪個密碼體系是以黎曼猜想的成立或者不成立作為設計基礎的。例如RSA，它的基礎是因數分解的困難性。如果我們證明了黎曼猜想，那麼當然會對質數的分佈增加很多瞭解，但這是否會導致更快的因數分解算法呢？至少目前沒有，將來有沒有不知道。這是一個假設性的問題，到時又會需要很多的研究。因此，黎曼猜想和密碼學之間的聯繫，只是一種間接的聯繫，而不是立竿見影、一觸即發的直接聯繫。

對黎曼猜想的意義和重要性瞭解了這麼多，那麼人們嘗試證明黎曼猜想的努力，達到什麼程度了呢？

基本的回答是：離真正解決問題，看起來還離得遠。具體的進展情況，我們下次來講。

下一期將是本系列的最後一期，技術性內容將會很少，而故事性與情懷性內容將會很多，相信所有的同學們都能有所收穫哦~