時間晶體：構想、爭議與實現_風聞

2021年11月30日， Nature刊發了谷歌量子計算機團隊實現時間晶體實驗的研究，將這一新領域再掀波瀾。時間晶體是2012年由理論物理學家、諾貝爾物理學獎得主維爾切克提出的一種新物質形態。隨着研究人員的不斷深入探索，時間晶體的理論與實驗均發生了巨大的改變。在理論方面，物理學家對最初提出的量子時間晶體概念進行了“圍攻”，後來提出了離散時間晶體的新概念。而在實驗方面，多項表明實現離散時間晶體實驗遭到爭議，其實驗呈現方式並非與理論概念吻合。在短短不到10年間，關於時間晶體的研究在各方團隊的質疑中迅速發展。在本文中，我們將見證物理學家如何突破自身侷限探索人類知識的邊界。

撰文 | 郭啓淏（南方科技大學）、尹璋琦（北京理工大學）

前言：近年來，量子計算實驗技術的發展為人類利用量子優越性加速信息處理和研究複雜量子物理系統帶來了無限可能。基於超導電路和光學系統，人們已在不同問題上展示了量子計算系統對經典計算機的優越性。與此同時，在量子計算機上進行的量子模擬，為物理學家研究新奇量子物態和拓撲材料開闢了新的道路。凝聚態物理學家得以打破紙面、數值模擬乃至現有材料的限制，探索更天馬行空的的物理概念。時間晶體，就是最近一個影響巨大的例子。本文將從時間晶體的來由講起，着重介紹多體局域化保護的離散時間晶體和實驗發展，及有關的激烈論戰，希冀讀者瞭解離散時間晶體理論，以及基於量子計算機的量子模擬。

2012-2015：否定之否定

時間晶體這一奇特的概念，源自諾貝爾物理學獎得主弗蘭克·維爾切克（Frank Wilczek）2012年提出的一個大膽設問：是否存在一種物質，當其處於基態附近時，在時間維度上會自發出現週期性變化，就像空間晶體在空間維度上自發出現週期性重複一樣。更為確切地説, 生活中常見的晶體源於眾多原子發生空間連續平移對稱性自發破缺，從而形成空間離散平移對稱的自組織結構。與其類似，維爾切克最初定義的時間晶體，則是在一個不含時系統，其基態發生的時間連續平移對稱性破缺，從而使其狀態及可觀測量發生週期性變化的時間自組織結構[1, 2]。

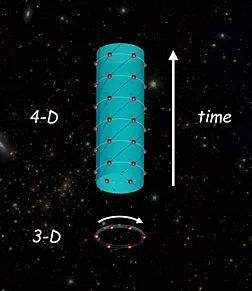圖1 時間晶體概念示意圖：離子形成的魏格納環晶體，當其處於基態時，離子依然保持轉動，這一空間-時間都平移對稱的體系稱為空間-時間晶體。丨來源：李統藏博士、張翔教授實驗組

沿着這條思路，維爾切克及其合作者分別提出了經典時間晶體和量子時間晶體的模型[1, 2]，同時加州大學伯克利分校的李統藏、張翔等人也提出了基於離子阱的量子時空晶體理論[3]。與經典時間晶體模型不同的是，量子時間晶體一問世即遭各家物理高手圍攻，前有法國萊布尼茨獎得主帕特里克·布魯諾 （Patrick Bruno），他指出維爾切克的量子時間晶體模型與李統藏等人的量子時空晶體理論在有限温情況下不能成立[4]，他稱之為時間晶體的“不存在定理”；後有日本凝聚態物理理論專家渡邊悠樹（Haruki Watanabe）等，他們從時間維度上的長程序出發，證明了有限温平衡態情況下，只具有短程相互作用的多體物理系統，在熱力學極限下不存在量子時間晶體[5]。僅僅誕生數年，時間晶體這一優美的物理模型，似乎就要被各家嚴謹的分析論證徹底否定了，但優美的模型總是冥冥之中被垂愛着的。儘管渡邊悠樹等人否定了能夠在平衡態物理系統中找到量子時間晶體，但其論證無法否定受到週期性調製的非平衡態系統中量子時間晶體存在的可能性[5]。基於此，一種被稱為離散時間晶體的模型被髮明瞭出來，並在隨後的幾年以驚人的速度蓬勃發展。‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬‬

2015-2018：走向現實

儘管破缺連續時間平移對稱性的量子時間晶體模型遭遇了極多困難，但自2015年克里斯托弗·薩查（Krzysztof Sacha）第一次明確地引入離散時間對稱性自發破缺這一概念以來[6]，離散時間晶體理論的發展呈現一片欣欣向榮。以諾曼·姚（Norman Y.Yao，2019年美國物理學會瓦利獎得主）、維迪卡·凱曼尼（Vedika Khemani，2020年美國物理學會瓦利獎得主）以及多米尼克·埃爾斯（Dominic V. Else）為代表的凝聚態科學家，從不同角度出發，最終完成了自旋系統中離散量子時間晶體模型的構建。

在介紹他們理論之前，我們先聊聊對稱性自發破缺，它是指大自然從一個物理系統所有允許的運動方程的解中特意挑選一些性質特殊的解。此時儘管物理系統本身的拉氏量（哈密頓量）具有某些對稱性，但系統運動狀態及可觀測量的行為卻具有更小的對稱性。具體到離散時間晶體而言，在週期性驅動（弗洛凱）系統中，系統哈密頓量具有以 為時間週期的離散時間平移對稱性，然而，離散時間晶體的可觀測量卻呈現為 為週期平移對稱結構（為大於1的正整數），我們稱之為“倍週期”行為。不僅如此，這個“倍週期”行為是穩定的，面對多體系統的子系統熱化、驅動週期的擾動、相互作用強度的擾動等，離散時間晶體總能保持其特立獨行的動力學[7, 8]。

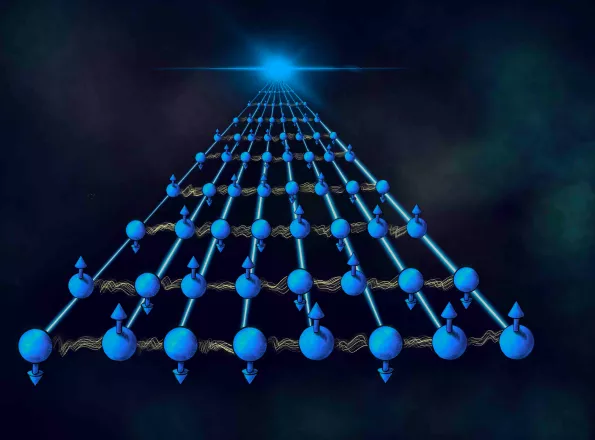圖2 離散時間晶體概念示意圖：一維1/2自旋鏈構成的時間晶體。系統的哈密頓量具有以時間T為週期的離散時間平移對稱性，使得T時間自旋鏈完全翻轉。因此可觀測量具有2T的離散時間平移對稱性。丨來源：Physics World

儘管週期性驅動系統當中可能存在量子時間晶體這一猜想早在2015年就已埋下伏筆[5]，一個棘手的問題卻一直橫亙在該方向的科學工作者面前：帶有驅動的相互作用多體自旋系統，大多服從熱本徵態假設，在演化過程中迅速地發生子系統熱化並被加熱到無限温態，以至於無法觀測到穩定的離散時間平移對稱性破缺現象[8, 9]。因此，長期關注可以規避量子熱化的多體局域化理論的諾曼·姚[7]，研究驅動自旋系統相結構的維迪卡·凱曼尼[10]，和研究對稱性保護拓撲相的多米尼克·埃爾斯[11]自然成為了這一領域的領跑者。他們都將注意力轉向了一類帶有多體局域化性質的驅動伊辛自旋鏈，單個週期T內驅動過程分為施加帶有失序的自旋1/2縱場伊辛模型和與之反對易的泡利X翻轉算符構成。由於該模型與一種具有馬約納拉π模的拓撲物相之間存在對應，這一模型又被稱為π-自旋玻璃[8]。對於製備在直積態上的自旋鏈而言，我們可以發現，儘管弗洛凱演化算符具有T為週期的時間平移對稱性，系統的每一個格點的磁化率，卻總是在2T後才能回到初始狀態，這也意味着這個系統的確發生了離散時間平移性對稱性破缺。此外，該模型還具有良好的性質：除了失序的縱場伊辛模型自身對相互作用擾動的容忍外，由於湧現的Z2對稱性的存在，該模型還容許在翻轉算符X的強度上有一定偏差。許多工作分析了該系統的長時間動力學與熱力學性質[7-13]，上述理論工作表明：一個可以實現的離散時間晶體模型似乎已經被找到。

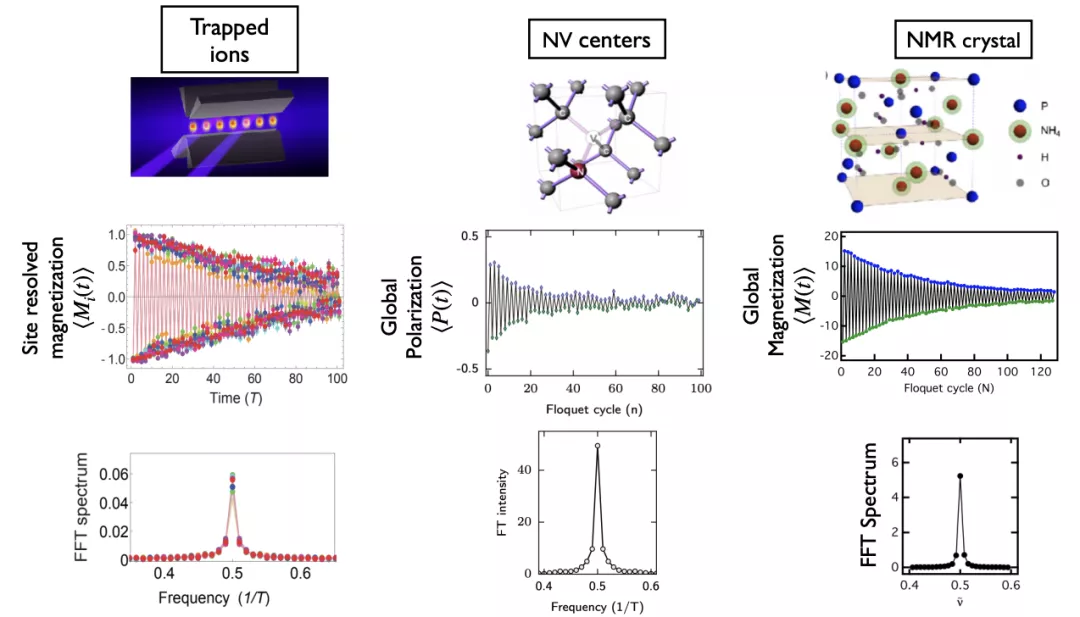圖3 離散時間晶體實驗圖，離子阱、金剛石色心繫統和核磁共振系統。圖上層：利用激光囚禁的鐿離子，金剛石中的隨機雜質和磷酸二氫銨晶體。中層：離散時間晶體磁化率的動力學。下層：離散時間晶體的次頻響應特徵（即“倍週期”特性）。丨來源：A Brief History of Time Crystal

在實驗平台上檢驗此理論自然就水到渠成了。如圖3所示，2017-2018年兩年間，來自馬里蘭大學的離子阱實驗團隊[14]、哈佛大學的金剛石色心實驗團隊 [15]和耶魯大學的核磁共振量子平台團隊[16]分別在《自然》、《物理評論快報》等頂尖刊物上報道了他們實現離散時間晶體並觀察其 “倍週期”行為的工作。這一消息不僅使得學界振奮，大眾媒體也爭相報道。但是在一派熱鬧氣氛下，學界的爭議卻並未停止，甚至在隨後的時間裏引發了更大的波瀾。

2018-2021: 風波再起

離散時間晶體實驗出現後，最主要的質疑是：這些被製造出來的離散時間晶體，是否真的是性質良好、永不熱化的多體局域化時間晶體，還是其中摻雜了其他的動力學機制[8]？

金剛石色心實驗與核磁共振實驗存在的問題最為突出。在金剛石色心實驗中，儘管具有較強的失序，但是其相互作用形式——三維長程偶極相互作用——與多體局域化並不相容。實驗組也承認這是一種最終還會熱化的“臨界時間晶體” [17]。核磁共振實驗則完全沒有失序，因此不屬於多體局域化保護的離散時間晶體。維迪卡·凱曼尼與其博士導師希瓦吉·桑迪提出，核磁共振版本的時間晶體基於一種被稱為“預熱化”的機制[8, 9]。在預熱化系統中由於存在一些對稱性和準守恆可觀測量[9, 18-20]，其熱化過程將會被抑制，因此提供了可以觀察離散時間晶體行為的窗口時間。但預熱化系統存在種種限制，比如預熱化機制只能保護一些接近系統基態的低温態的動力學，只能保護系統在指數時間內不完全熱化等，較之近乎永不熱化的多體局域化系統仍顯平庸。打個比方來説，如果説多體局域化系統是度過天劫永生不滅的金仙，那預熱化系統只算是剛剛結出元嬰，比一般量子系統活得長些而已。維迪卡·凱曼尼與希瓦吉·桑迪還提出了檢驗預熱化離散時間晶體性質的方案。其中不少論斷被馬里蘭大學的離子阱實驗團隊在預熱化離散時間晶體的實驗中證實，該工作隨後發表在《科學》雜誌上[20]。筆者也與中國科學技術大學朱曉波老師團隊，在超導系統上完成了類似的弗洛凱預熱化機制的實驗 [21]。

隨後，爭論的焦點就轉移到了離子阱版本的離散時間晶體上，由於具有失序和多體局域化相容的相互作用形式，該工作曾被一度認為是首個多體局域化離散時間晶體工作。但是由於該實驗的模型在數值試驗中展現出初態依賴性，以及實驗中自旋鏈長度較短（只有10個），支持多體局域化的證據並不充分。2021年9月1日，維迪卡·凱曼尼等人正式向諾曼·姚等人發難[22]，從有效哈密頓量形式、尺寸效應和邊界條件等數個問題質疑姚等人的理論模型。維迪卡·凱曼尼等人指出，此前離子阱上的實驗雖然具有多體局域化必需的失序，但是其單格點上的失序並不能在弗洛凱動力學中扮演阻止其熱化的角色。他們通過對兩週期演化算符分析，發現可以通過反對易關係精確地消除有效哈密頓量中的失序，因此該系統在演化過程中並不能產生弗洛凱多體局域化的效果[8, 22]。因此，離子阱上的實驗也可以被視作一個預熱化機制保護的離散時間晶體。維迪卡·凱曼尼等人也列出了他們數值結果，根據離子阱上的實驗設計，該離散時間晶體並不能遍歷所有直積態，對於一些高温態，系統會在數十個弗洛凱週期中迅速熱化，令人無法觀察到穩定的離散時間晶體動力學。此外，由於有限尺寸和邊界效應的存在，該實驗還存在一些漏洞。維迪卡·凱曼尼等人還指出了在諾曼·姚等人模型基礎上實現多體局域化離散時間晶體的條件，即相互作用強度也須具有較大的失序，這樣才不會出現有效哈密頓量中沒有失序的情況。

兩週後的9月15日，諾曼·姚等人做出了回應[23]，他們把維迪卡·凱曼尼等人的模型稱為KMS（Khemani-Moessner-Sondhi）模型，將自己的模型稱為YPPV（Yao-Potter-Potirniche-Vishwanath）模型。諾曼·姚等人通過數值實驗展示了對於足夠小的可積性破壞橫場，他們的系統確實可以使任意直積態保持振盪。但是諾曼·姚等人也承認，對一些“搗蛋”的初態，他們模型的週期性振盪振幅會比較小。進一步地，通過有限尺寸的外推和對邊界條件的分析，姚等人堅持他們的觀點，他們的離散時間晶體實驗並不是僅僅由於預熱化效應所造成的，而是確實是具有量子多體效應參與的。在2021年早些時期，諾曼·姚等人在金剛石色心繫統上又設計了一種多體局域化離散時間晶體的實驗[24]，實驗現象顯示無初態依賴，並且能夠維持800個弗洛凱週期以上，較離子阱的實驗更具有説服力。

綜合上述質疑與答覆，筆者認為，諾曼·姚等人的模型並沒有完全展示真正的多體局域化離散時間晶體行為，但是眾多現象也顯示了此係統的確有一部分量子多體效應參與。這場學術角鬥誰贏誰輸，還沒有到可以下定論的時候。

利用數字量子模擬中製造多體局域化時間晶體

其實在2020年6月，維迪卡·凱曼尼和希瓦吉·桑迪等人已在預印本網站arXiv上掛出來，他們打算在谷歌超導量子處理器懸鈴木上實現多體局域化離散時間晶體的方案[25]。一年以後，谷歌團隊以KMS模型為基礎實現了離散時間晶體，2021年11月30日《自然》雜誌在線發表此工作[26]。該實驗相較之前的所有離散時間晶體方案來説具有很大的進步。

首先是自旋鏈的長度：谷歌團隊使用了鏈狀的20個超導比特實現時間晶體，從而真正進入了量子多體系統區域，使得尺寸效應和邊界效應的影響足夠小。其次，完全使用數字量子模擬來實現多體局域化時間晶體的哈密頓量，即完全使用量子門電路“拼”出來想要的哈密頓量。這比之前使用量子比特之間原生相互作用的類比量子模擬方案，具有更大的可操控性，但是其實現更為困難。在谷歌的實驗中，他們使用單比特門和兩比特的費米子模擬門來實現多體局域化時間晶體的哈密頓量。為避免預熱化機制的干擾，谷歌團隊對完全極化的初態，尼爾態以及隨機的二進制字符串態都進行了實驗。實驗結果顯示，他們的系統不僅展示出了離散時間晶體的“倍週期”動力學，也確實滿足弗洛凱多體局域化不依賴於初態的特性。此外，他們還測量一個新的可觀測量——自旋玻璃序參量[25, 26]，這個序參量的隨着系統尺寸的行為展示了其確實滿足 -自旋玻璃特性。因此該實驗從方案設計上的確是目前最為滿足多體局域化離散時間晶體要求的。利用輔助比特測量自旋時間關聯函數的方法也較之前的實驗更嚴謹。

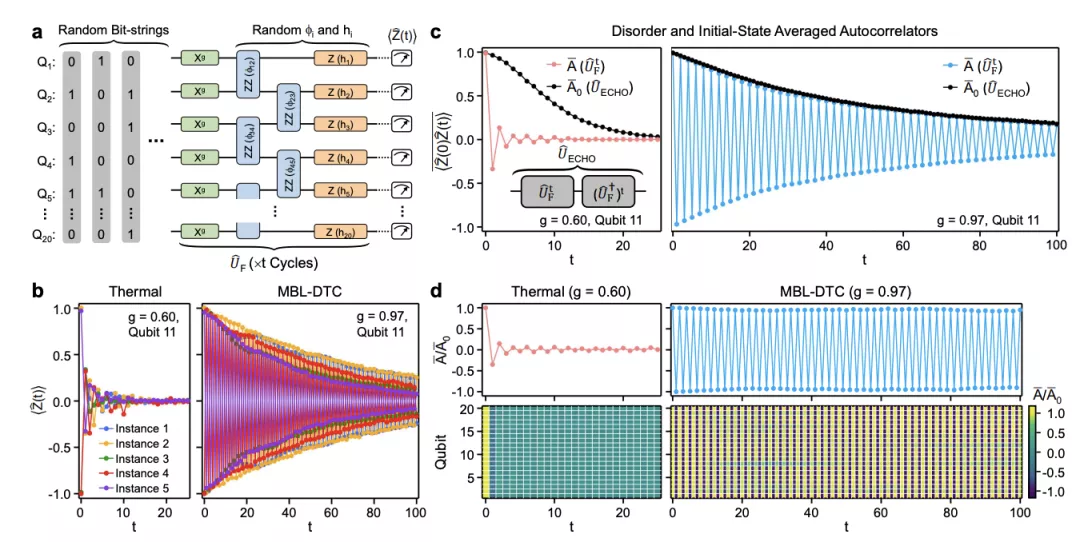圖4 谷歌時間晶體實驗示意圖。(a)：製造離散時間晶體的過程，將系統初態製備到二進制字符串態。通過數字量子模擬方法，用量子門電路模擬離散時間晶體的哈密頓量，並在結束時讀取其Pauli-z算符的期望。(b)：對於不同初態和失序取平均的離散時間晶體動力學。(c)：熱化系統的行為和多體局域化離散時間晶體行為的對比。(d)：通過回聲線路進行降噪後獲得的無退相干影響的離散時間晶體動力學。丨來源：谷歌離散時間晶體預印本Observation of Time-Crystalline Eigenstate Order on a Quantum Processor

該實驗也展示出谷歌超導量子計算團隊優秀的技術能力。在實驗前，谷歌團隊對費米子模擬門進行了精細地交叉熵基準測試和弗洛凱校對。並且在實驗後通過回聲線路進行降噪處理，極大降低了實驗中超導量子比特退相干帶來影響，使得實驗數據更為漂亮。需要指出的是，我國量子計算實驗團隊也做出了自己的貢獻——北京量子信息科學研究院於海峯團隊在超導比特系統上，通過類比量子模擬成功實現了基於YPPV模型的離散時間晶體[27]；浙江大學王浩華團隊實現了一類基於對稱性保護拓撲態的邊界時間晶體[28]。除此之外，還有不少離散時間晶體模型等待進一步發掘，諸如經典預熱化離散時間晶體[29, 30]、基於元胞自動機的離散時間晶體[31]， 等等。離散時間晶體從奇思妙想一步步演變為嚴謹周密的物理模型，對量子模擬和新穎量子物質領域影響巨大，並促使凝聚態理論物理學家和量子物理實驗科學家聯起手來，探索更多有趣的人造物態。

未來可期

2021年9月，諾曼·姚、維迪卡·凱曼尼、多米尼克·埃爾斯和渡邊悠樹四位理論科學家共同獲得“科學突破獎”，標誌着離散時間晶體這一新領域獲得了更廣泛的認可。2021年底，谷歌量子計算團隊所實現的離散時間晶體實驗，被美國物理學會（APS）Physics和英國物理學會（IOP）Physics World評為年度物理學突破之一。對離散時間晶體的研究，刷新了人們對了週期性驅動系統、多體局域化、預熱化以及量子熱化過程等領域的理解，並促使更多不同領域的科研工作者投身其中。從離散時間晶體的發展過程可以看出，科學探索在大多數時候都不是一番風順的，需要否定之否定，以及學術上針鋒相對的論戰。在科學探索中，有創見的錯誤比平庸的正確更有價值，因為錯誤中可能孕育着新的思想。時間晶體正好趕上了量子計算技術突飛猛進，才得以在短時間內獲得迅猛發展而非被埋沒。這引發我們深思：理論和實驗應當如何看待彼此，應該如何合作，才能推動一個科學領域不斷前行？

參考文獻

[1] Shapere, Alfred, and Frank Wilczek. “Classical time crystals.” Physical review letters 109.16 (2012): 160402.

[2] Wilczek, Frank. “Quantum time crystals.” Physical review letters 109.16 (2012): 160401.

[3] Li, Tongcang, et al. “Space-time crystals of trapped ions.” Physical review letters 109.16 (2012): 163001.

[4] Bruno, Patrick. “Impossibility of spontaneously rotating time crystals: a no-go theorem.” Physical review letters 111.7 (2013): 070402.

[5] Watanabe, Haruki, and Masaki Oshikawa. “Absence of quantum time crystals.” Physical review letters 114.25 (2015): 251603.

[6] Sacha, Krzysztof. “Modeling spontaneous breaking of time-translation symmetry.” Physical Review A 91.3 (2015): 033617.

[7] Yao, Norman Y., et al. “Discrete time crystals: Rigidity, criticality, and realizations.” Physical review letters 118.3 (2017): 030401.

[8] Khemani, Vedika, Roderich Moessner, and S. L. Sondhi. “A brief history of time crystals.” arXiv preprint arXiv:1910.10745 (2019).

[9] Luitz, David J., et al. “Prethermalization without temperature.” Physical Review X 10.2 (2020): 021046.

[10] Khemani, Vedika, et al. “Phase structure of driven quantum systems.” Physical review letters 116.25 (2016): 250401.

[11] Else, Dominic V., Bela Bauer, and Chetan Nayak. “Floquet time crystals.” Physical review letters 117.9 (2016): 090402.

[12] Sacha, Krzysztof, and Jakub Zakrzewski. “Time crystals: a review.” Reports on Progress in Physics 81.1 (2017): 016401.

[13] Else, Dominic V., et al. “Discrete time crystals.” Annual Review of Condensed Matter Physics 11 (2020): 467-499.

[14] Zhang, Jiehang, et al. “Observation of a discrete time crystal.” Nature 543.7644 (2017): 217-220.

[15] Choi, Soonwon, et al. “Observation of discrete time-crystalline order in a disordered dipolar many-body system.” Nature 543.7644 (2017): 221-225.

[16] Rovny, Jared, Robert L. Blum, and Sean E. Barrett. “Observation of discrete-time-crystal signatures in an ordered dipolar many-body system.” Physical review letters 120.18 (2018): 180603.

[17] Ho, Wen Wei, et al. “Critical time crystals in dipolar systems.” Physical review letters 119.1 (2017): 010602.

[18] Ueda, Masahito. “Quantum equilibration, thermalization and prethermalization in ultracold atoms.” Nature Reviews Physics 2.12 (2020): 669-681.

[19] Peng, Pai, et al. “Floquet prethermalization in dipolar spin chains.” Nature Physics 17.4 (2021): 444-447

[20] Kyprianidis, Antonis, et al. “Observation of a prethermal discrete time crystal.” Science 372.6547 (2021): 1192-1196.

[21] Ying, Chong, et al. “Floquet prethermal phase protected by u (1) symmetry on a superconducting quantum processor.” arXiv preprint arXiv:2107.07311 (2021).

[22] Khemani, Vedika, Roderich Moessner, and S. L. Sondhi. “A comment on” Discrete time crystals: rigidity, criticality, and realizations"." arXiv preprint arXiv:2109.00551 (2021).

[23] Yao, Norman Y., et al. “Reply to Comment on” Discrete Time Crystals: Rigidity Criticality and Realizations"." arXiv preprint arXiv:2109.07485 (2021).

[24] Randall, J., et al. “Many-body-localized discrete time crystal with a programmable spin-based quantum simulator.” Science (2021): eabk0603.

[25] Ippoliti, Matteo, et al. “Many-body physics in the NISQ era: quantum programming a discrete time crystal.” PRX Quantum 2.3 (2021): 030346.

[26] Mi, Xiao, et al. “Time-Crystalline Eigenstate Order on a Quantum Processor.” Nature (2021): https://doi.org/10.1038/s41586-021-04257-w.

[27] Xu, Huikai, et al. “Realizing discrete time crystal in an one-dimensional superconducting qubit chain.” arXiv preprint arXiv:2108.00942 (2021).

[28] Zhang, Xu, et al. “Observation of a Floquet symmetry-protected topological phase with superconducting qubits.” arXiv preprint arXiv: 2109.05577 (2021).

[29] Ye, Bingtian, Francisco Machado, and Norman Y. Yao. “Floquet phases of matter via classical prethermalization.” Physical Review Letters 127.14 (2021): 140603.

[30] Pizzi, Andrea, Andreas Nunnenkamp, and Johannes Knolle. “(Classical) Prethermal phases of matter.” arXiv preprint arXiv:2104.13928 (2021).

[31] Zhuang, Quntao, et al. “An absolutely stable open time crystal.” arXiv preprint arXiv:2110.00585 (2021).

特 別 提 示

1. 進入『返樸』微信公眾號底部菜單“精品專欄“，可查閲不同主題系列科普文章。

2. 『返樸』提供按月檢索文章功能。關注公眾號，回覆四位數組成的年份+月份，如“1903”，可獲取2019年3月的文章索引，以此類推。

版權説明：歡迎個人轉發，任何形式的媒體或機構未經授權，不得轉載和摘編。轉載授權請在「返樸」微信公眾號內聯繫後台。