牛頓與科學史爭端（轉載）_風聞

牛頓的科學史爭端

中國科學技術大學物理學院 林深茂 羅澤宇​

摘要

通過查閲牛頓生平的往來信件，梳理了平方反比力發現與證明的時間線。推斷出胡克先於牛頓提出平方反比律的猜想，但最終由牛頓完成了平方反比力與橢圓軌道關係的證明。通過查閲牛頓生平往來信件，梳理了微積分產生的思想流程，推斷出萊布尼茲和牛頓獨立的提出了微積分基本定理，且萊布尼茲的微積分方法更為現代

關鍵詞

牛頓、胡克、 萊布尼茲、 平方反比律、 橢圓軌道、微積分、 微積分基本定理 、級數

目錄

摘要

關鍵詞

目錄

一．牛頓生平

二．爭端

（一）   胡克

a)      平方反比律

b)     爭端趣事

（二）   萊布尼茲

a)      微積分

b)     爭端趣事

三．總結

四．參考文獻

五．附錄

a)       微積分的奠基

b)       微積分的產生

c)        附錄總結

六．附錄參考文獻

 一．牛頓生平

圖一

      牛頓出生於公元1642年12月25日,那天是基督教的聖誕節，地點在英國的林肯郡伍爾索普鎮。牛頓家境貧寒，父親是個小農場主，在牛頓出生以前三個月就已經去世，那時他的生身父母結婚才半年多。牛頓3歲時母親改嫁給一位牧師，是外祖母把他撫養大。12 歲時他的繼父又去世,他回到了母親身邊，發現自己多了三個同母異父的弟妹。牛頓的小學教育，主要是在外祖母家完成的。 

牛頓在離家較遠的格蘭薩姆文科學校讀中學，寄宿在一位藥劑師的家中。在那裏，他獲得了極為寶貴的廣泛閲讀各類書籍，製作各種玩具，從事多種化學、物理實驗的機會。

牛頓的童年沒有得到父愛和母愛,這種不幸使小牛頓性格孤僻內向。他沒有知心朋友,他的課餘時間全都獻給了如飢似渴的閲讀和興趣盎然的實驗。但是他的學習成績不好，一度還是班級裏倒數第二。直到有一次他與一個欺負他的同學打架並且贏得了那場本來實力懸殊的毆鬥 ,他萌發出強烈的上進心,天才的一面開始展現出來，成績也一躍進入前茅。

牛頓中學畢業後以優異成績被推薦到劍橋大學三一學院。他極其勤奮地讀書、思考，他研究了大量古代和當代人的著作，特別是有關自然哲學、數學和光學方面的。不久他的指導教師就發現這個學生的學識已經超過了自己。1665 年和1666年間，英國流行大鼠疫，各大學師生被疏散，牛頓回到家鄉。在這18個月裏，牛頓度過了他一生中最富於創造力的階段。

 

圖二

      牛頓晚年回憶道：“1665年初，我發現了逼近級數法和把任意二項式的任意次冪化成這樣一個級數的規則。同年5月,我發現格里高利(Gregory，James，1638-1675)和司羅斯(Slues, Rene-Francois de，1622-1685)的切線方法。11月,得到了直接流數法。次年1月，提出顏色理論。5月裏我開始學會反流數方法。同一年裏，我開始想到引力延伸到月球軌道(並且發現計算使小球緊貼着內表面在球形體內轉動的力的方法)，並且由開普勒定律，行星運動週期倍半正比於它們到其軌道中心距離，我推導出使行星維繫於其軌道上的力，必定反比於它們到其環繞中心距離的平方。因而，對比保持月球在其軌道上的力與地球表面上的重力，我發現它們相當相似。所有這些都發生在1665-1666那兩年的大鼠疫期間。那時，我正處於發明初期，比以後任何時期那更多地潛心於數學和哲學。”

1667年劍橋大學復課，牛頓當選為三一學院院士。兩年後，牛頓接替著名的數學家巴羅(Isaac Barrow，1630-1677)任魯卡斯教席數學教授。1668年牛頓發明並製作出第一台反射望遠鏡，1671年他製作了第二台並贈送給英國皇家學會，不久當選為該學會會員。在科學研究中嶄露頭角的牛頓遭到胡克（Robert Hooke，1635-1702)等人的習難，捲入曠日持久的關於光的本性的爭論；約10年後牛頓與胡克之間又發生關於引力和運動學方面的爭論；在《原理》寫作期間(1686)和出版後，牛頓與胡克又發生關於發現萬有引力的優先權問題的爭論；同時牛頓與德國人萊布尼茲( Wilhelm Gottfried Leibnitz，1646-1716)之間又發生關於微積分的發明權的爭論。

1679年，牛頓與胡克的爭吵十分激烈。胡克對牛頓關於引力的見解提出強烈質疑，這促使牛頓全面考察了開普勒(Johannes Kepler,1517-1630)定律、加利略(Galileo Galiei,1564- 1642)運動學公式與引力之間的關係。這一年牛頓終於證明了引力的平方反比關係與行星橢圓軌道之間的對應關聯。至此，牛頓的整個宇宙體系和力學理論的基本框架宣告完成。

圖三 萊布尼茲

牛頓在1684年才進入寫作《原理》的準備階段。到那一年，哈雷（Edmond Halley，1656-1743）、胡克和雷恩（Christopher Wren，1632-1723）三人大約同時猜到引力的平方反比關係與行星的橢圓軌道之間有必然聯繫，但他們都無法證明這一點。哈雷請教牛頓，牛頓表示他在幾年前已經證明了這一點，但是原先的手稿找不到了，他可以給哈雷再證明一遍。牛頓重新寫出了一篇《論軌道上物體的運動》，文中證明，天上與地上的物體服從完全同樣的運動規律，引力的存在使得行星及其衞星必定沿橢圓軌道運動。

哈雷一眼看出這篇論文有劃時代的價值，他敦促牛頓把它擴充為專著發表。於是1685和1686兩個年份的18個月裏，牛頓專心致志地從事寫作，《原理》這部偉大著作從牛頓的筆下源源不斷地流淌出來。牛頓顯然是有長期研究所取得的豐富成果作為基礎，他寫下的論述事無鉅細，都經過深思熟慮。他的寫作速度之快令人驚異，他寫作時的專注忘我令人感佩。

值得一提的是，皇家學會雖然十分重視牛頓的《原埋》，但卻沒有財力資助出版它，是

哈雷自費出版了牛頓的這部著作。

《原理》的出版震動了整個英國和歐洲學界。牛頓一躍成為當時歐洲最負盛名的數學家、天文學家和自然哲學家。人們爭相向他表示敬意。英國王室請他做客，歐洲公認的最偉大的幾何學家惠更斯(Christiaan Huygens，1629-1695)專程到英國拜訪他，各國元首和貴族訪問英國時也要去看望他，以結識他為榮。1689年，牛頓當選為國會議員；1696年，牛頓獲得造幣局總監任命；1701年，他再次當選國會議員；1703年，當選為英國皇家學會會長；1705年，受女王冊封成為爵士。

圖四 《自然哲學的數學原理》

     《原理》第一版出版時牛頓43歲。他的後半生研究強度大大減少，1704年他的另一重要著作《光學》出版，這本書是以英語寫作的。1707年他出版了《數學通論》，這部著作沒有引起廣泛重視。在他生前，《原理》出版三個版本，第二版在1713年，第三版在1726年。

牛頓的後半生主要從事的工作和活動有

社會活動。他應付各類社會名流賢達的拜訪，從事國家造幣局的管理工作，管理皇家學會。

與胡克、弗拉姆斯蒂德(John Flamsteed，1646 -1719)、萊布尼茲等人爭論。

研究神學和《聖經》。

研究鍊金術。

整理出版自己的著作和文稿。

牛頓終生未娶，1727年3月20日逝世，英國王室為他在西敏寺大教堂舉行了國葬。[1]

  二．爭端

（一）   胡克

a)      平方反比律

       1686年，在哈雷的鼓勵下，牛頓將專著《自然哲學的數學原理》交給皇家學會審議，在這次會議上，胡克提出引力反比定律是自己告訴牛頓的，牛頓應該在專著的前言指出自己的貢獻。牛頓並未參加這次會議，事後也未接受胡克的要求，在他看來，自己1666年就發現了引力的平方反比定律，並且寫信告訴了他人，因此自己是這一定律的發現者。

        在《the correspondence of Isaac Newton》系列叢書中收錄了牛頓從1661年到1727年間的信件內容，然而，在其中並未找到牛頓所聲稱的1666年發現引力平方反比律並寫信給他人的信件。         

        在1679到1680年間牛頓與胡克進行了頻繁地信件交流，胡克向牛頓問了落體問題並給出了一些假設，而從牛頓當時的回信來看他並沒有認識到平方反比律以及與之相應的落體軌道形狀。以下是1679年牛頓給胡克的第一封回信：

28 NOVEMBER 1679

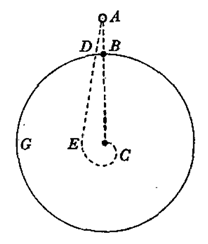
In requital of this advertisement I shall communicate to you a fansy of my own about discovering the earth’s diurnal motion. In order thereto I will consider ye Earth’s diurnal motion alone without ye annual, that having little influence on ye experimt I shall here propound. Suppose then BDG represents the Globe of ye Earth carried round once a day about its center C from west to east according to ye order of ye letters BDG; & let A be a heavy body suspended in the Air & moving round with the earth so as perpetually to hang over ye same point thereof B. Then imagin this body B let fall & it’s gravity will give it a new motion towards ye center of ye Earth without diminishing ye old one from west to east. Whence the motion of this body from west to east, by reason that before it fell it was more distant from ye center of ye earth then the parts of ye earth at wch it arrives in its fall, will be greater then the motion from west to east of ye parts of ye earth at wch ye body arrives in it’s fall: & therefore it will not descend in ye perpendicular AC, but outrunning ye parts of ye earth will shoot forward to ye east side of the perpendicular describing in it’s fall a spiral line ADEC, quite contrary to ye opinion of ye vulgar who think that if ye earth moved, heavy bodies in falling would be outrun by its parts & fall on the west side of ye perpendicular. The advance of ye body from ye perpendicular east- ward will in a descent of but 20 or 30 yards be very small & yet I am apt to think it may be enough to determin the matter off act. Suppose then in a very calm day a Pistol Bullet were let down by a silk line from the top of a high Building or Well, the line going through a small hole made in a plate of Brass or Tinn fastened to ye top of ye Building or Well & yt ye bullet when let down almost to ye bottom were setled in water so as to cease from swinging & then let down further on an edge of steel lying north & south to try if ye bullet in setling thereon will almost stand in 12quilibrio but yet with some small propensity (the smaller ye better) decline to ye west side of ye steel as often as it is so let down thereon. The steel being so placed underneath, suppose the bullet be then drawn up to ye top & let fall by cutting clipping or burning the line of silk, & if it fall constantly on ye east side of ye steel it will argue ye diurnall motion of ye earth. But what ye event will be I know not having never attempted to try it. If,any body may think this worth their triall the best way in my opinion would be to try it in a high church or wide steeple the windows being first well stopt. For in a narrow well ye bullet possibly may be apt to receive a ply from ye straitned Air neare ye sides of ye Well, if in its fall it come nearer to one side then to another. It would be convenient also that ye water into wch ye bullet falls be a yard or two deep or more partly that ye bullet may fall more gently on ye steel, partly that ye motion wch it has from west to east at its entring into ye water by meanes of ye longer time of descent through ye water, carry it on further eastward & so make ye experiment more manifest. [2]

大致：B點在地球上隨地球自轉，A點固定在它的正上方。則A處物體下落時將不沿ABC而是沿着ADEC。而按照牛頓自己的説法，他在1666年就發現了平方反比律並告訴了他人。如果他真的已經掌握了平方反比律，那麼此處探討中的軌跡假設就應當為：1. 若把地球的質量都集中在球心一點，有心力反比與r的二次冪，軌跡應為橢圓。2. 若把地球看做一實心球體，則易知有心力等效為r的一次冪，軌道同樣應為橢圓。

證明如下：

在極座標系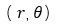討論，引力常數為G，地球質量M，物體質量m

易知在有心力場中角動量守恆（設角動量為J）：

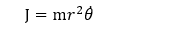            (1)

能量守恆（設總能量為E）:

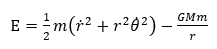    (2)

(1)(2)聯立，推出：

      (3)

此即為物體墜落的軌跡微分方程，解之可得：

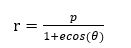     (4)

其中：

                                                                    

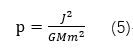
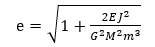   (6)

此即為圓錐曲線軌道（E<0時為橢圓軌道）

正比於r的一次冪同理可證。

1674年，胡克發表《試證地球的運動》，文中總結了行星運動的理論：一切天體都受到引力 的作用；如果天體不受引力作用，將保持直線運動；天體離引力中心越近，受到的引力越大。這其實是萬有引力的定性描述，後來胡克進一步發現了引力的平方反比定律，並在1680年給牛頓的一封信中提到這點。

6 JANUARY 1680

But my supposition is that the Attraction always is in a duplicate proportion to the Distance from the Center Reciprocall, and Consequently that the Velocity will be in a subduplicate proportion to the Attraction and Consequently as Kepler Supposes Reciprocall to the Distance. And that with Such an attraction the auges will unite in the same part of the Circle and that the neerest point of accesse to the center will be opposite to the furthest Distant.[4]

“但我的假設是吸引力總是與到中心的距離成平方反比的，而速率與吸引力成平方根關係，因此就像開普勒假設的那樣速率與距離成反比。在這樣的引力下，頂點將會集合在軌道的同一位置（軌道閉合），近中心點將會與軌道距中心最遠的距離相對。”

 b)     爭端趣事

在科學研究中嶄露頭角的牛頓遭到胡克（Robert Hooke，1635-1702)等人的習難，捲入曠日持久的關於光的本性的爭論。

胡克繞過皇家學會，同牛頓直接通信，二人進行了一番看似彬彬有禮實則互相譏諷的通信。1676年1月，胡克在給牛頓的信中寫道：“我確認你在這方面所下的功夫比我深得多，也確信無法找到比你更適合、更能幹的人來研究這些題材……如果我從事的職務允許的話，這都是我自己想完成的事，儘管我很清楚這只需要具有比你稍微低一些的才能就可以。”

That I judge you have gone farther in that affair much than I did, and that as I judge you cannot meet with any subject more worthy your contemplation, so I believe the subject cannot meet with a fitter and more able person to inquire into it than yourself, who are every way accomplished to compleat, rectify and reform what were the sentiments of my younger studies, which I designed to have done somewhat at myself if my other more troublesome employments would have permitted, though I am sufficiently sensible it would have been with abilities much inferior to yours. [5]

1676年2月5日，牛頓回信胡克，信中寫道：“笛卡爾（的光學研究）踏出了很好的一步，而你則推進了許多方面的發展……如果我看得更遠一點的話，是因為我站在巨人的肩膀上。”牛頓這番話看似謙恭，是在恭維胡克，實則不然，胡克本人身材不高，而且有駝背的毛病，牛頓這句話自然有侮辱之嫌。

What(S) Des-Cartes did was a good step. You have added much several ways, & especially in taking ye colours of thin plates into philosophical consideration. If I have seen further it is by standing on ye sholders of Giants.[6]

笛卡兒（的光學研究）邁出了很好的一步。你在一些方面又增添了許多，特別是對薄板顏色進行了哲學考慮。如果我看得更遠一點的話，是因為我站在巨人的肩膀上。

這場爭論的結果是，牛頓決定等胡克死後再發表有關光學的論著，在這部1704年——胡克死後的第二年——出版的著作中，牛頓完全不提胡克對薄板顏色研究的貢獻。

        二人往來書信盡皆禮貌謙遜，以下為其中一封牛頓給胡克信得原件

 

圖五

 細節：

 

圖六

For his honoured Friend——Mr Gobirt Hooke——at his Lodgings in Gresham College in London

 

圖七

Your humble servant

Is. Newton

（二）   萊布尼茲

    a)      歷史資料

       為了使得行文更加流暢，我們決定在這裏着重給出萊布尼茲和牛頓的書信往來以及歷史資料來説明萊布尼茲和牛頓是各自獨立的完成了微積分的創作，牛頓率先發明而未發表，萊布尼茲晚些時候同樣得出了相同的結果，並且在相對較早的時候將其發明了出來。而在附錄中，我會詳細的介紹微積分的整個發展流程，對比牛頓和萊布尼茲二者的工作思想以及其一脈相承的思路，從而使得讀者更加清楚的認識到二者思想的不同。 

       微積分的爭端，主要集中在其起源上面。牛頓擁有着最早的微積分手稿（牛頓自稱自己在17世紀60年代中期就建立了“流數術”，即早期的微積分內容），而萊布尼茲則擁有了微積分第一篇論文——《一種求極大極小以及切線的奇妙類型的新方法，對有理量和無理量都是用，一種值得注意的演算》。（1684年發表於《教師學報》）下面我們首先討論牛頓的“流數術”的具體創立時間，判斷其流數術是否早於萊布尼茲的微積分誕生。

  請允許我插入一段關於萊布尼茲的微積分的建立完備的證據：

該圖摘自牛頓書信集（英文名為《The Correspondence of Issac Newton》）[7]第208封，在1677年的五月或者六月，我們可以清晰的看到萊布尼茲已經可以熟練的使用他的積分號並進行相關的運算了。至此，我們起碼可以斷定，萊布尼茲的微積分的產生不會晚於這個時間，而微積分基本定理的產生，從文章發表這個角度來説，萊布尼茲在1675年年末建立了微積分基本定理，而其論證在1693年給出。因此我們姑且可以證實，萊布尼茲關於微積分的研究在1675-1677年就已經完成的差不多了，而微積分基本定理的給出略晚，約1677年。因此萊布尼茲的微積分體系完全建立晚於1677年。下面我們看看牛頓在幾乎同時期的工作。

1666年10月完成了一篇沒有發表的總結性論文名為《1666年10月流數簡論》。但是遺憾的是，並未找到其他的佐證。因此在這裏暫不採信這一個説法而使用另外一種更加清晰的證明：

在上面的有關微積分的提出的思路中，我們可以清晰的看到，牛頓從流數（即對時間的微分）入手，提出了相關的級數理論和用牛頓法求解方程根（收錄於《分析學》，正式發表於1711）並根據級數反演法和流數術給出了sinx和cosx的冪級數的結果。以上內容均正式發表於1736年《流數法》一書中，並不能成為其早於萊布尼茲創建微積分的直接證據。

而直接證據是，是萊布尼茲和牛頓的直接書信往來，內容如下：

1676年5月12日之前，萊布尼茲得到了格雷戈裏給科林斯的一封關於級數論證的信，其內容含有三角函數和反三角函數的級數展開，而萊布尼茲並不能知道其中的係數的推理方式，於是寫信給英國皇家協會秘書奧爾登堡詢問如何求解無窮級數並用什麼方法才能使用無窮級數表示方程的根[8]

1676年5月左右，奧爾登堡回信中有如下內容“I know that the Segmts of Circles are of great use in practice, but if the Segmt be little Mr Newton Series which you sent me is not of ready use, and therefore you may make use of this:” [9]

顯然，此時的奧爾登堡已經知道牛頓做出了這個工作並且和是和格雷戈裏相互獨立進行的，而牛頓對此問題的證明的基礎就是微積分基本定理，因此我們可以從這裏推知牛頓此時已經完全構建完成了微積分的知識。

由此我們可以確定一個問題——即牛頓早於萊布尼茲發現了微積分的內容。因此，可以説微積分是由牛頓率先創立的。在《微積分的歷史和起源》（作者為萊布尼茲）一書中，萊布尼茲以第三人稱聲稱自己獨立創立了微積分顯然是不合適的。

另外，根據牛頓以及後期英國學者對萊布尼茲的抨擊，主要在於兩個方面，其一是萊布尼茲在和英國皇家學會中往來信件的內容中得到了微積分的相關處理方法，從而建立了微積分的內容，另一個方面是關於萊布尼茲級數，他們認為萊布尼茲級數（萊布尼茲於1674年發現）是抄襲英國數學家格雷戈裏的arctanx的展開形式的。下面我們從信件的角度來分析一下這個內容：

關於內容一，時間線如下：

在1676年之前，萊布尼茲和英國皇家學會的主要信件主要集中在1674年前後，主要是萊布尼茲在告訴皇家學會自己的一些幾何的成果以及在二項式展開上面的一些問題，那是並沒有相關微積分的內容往來[10]

在1676年萊布尼茲詢問牛頓和微積分有關的問題的時間線：

1.1672年12月10日，《通報》（牛頓和他的追隨者關於微積分的調查）萊布尼茲看過一封牛頓關於切線的心，流數方法在這封信中十分清楚，“任何聰明人“從中都可以得到微積分[11]

2.1673年，萊布尼茲作為美因茨大主教，訪問倫敦見到了皇家學會秘書奧爾登堡，並被推舉為皇家學會會員[12]

3.1673年，拜訪奧爾登堡，可能會看到牛頓《論分析》的抄本[13]

4.1676年，再次回到倫敦，訪問了牛頓的同時約翰科林斯，並看了些牛頓的論文[14]

5.1676.5.12 萊布尼茲詢問sinx和arcsinx的展開形式[15]

6.1676.6 奧爾登堡給牛頓寫信：“Though the modesty of Mr.Leibniz, in the extracts from his letter which you have lately sent me “把信轉交給了牛頓[16]

7.1676.6.12 牛頓回信並介紹了二項式定理：[17]

8.1676.8月，萊布尼茲備忘錄裏面內容表示他理解了二項式定理的相關內容

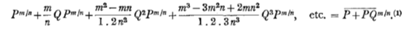[18]

9.1677年，萊布尼茲給奧爾登堡的一封回信中，就使用了自己的微積分理論計算了切線以及相關的最值問題的一些證明。而這個細節也被牛頓多次提及，1687年出版的《自然哲學的數學原理》第一版和第二版中寫道“十年前我和最傑出的幾何學家萊布尼茲的通信中，我表明我已經知道確定極大值和極小值的方法，做切線的方法以及類似的方法，但我在交換的信件中隱瞞了這一點….這位最傑出的科學家在回信中寫道，他也發現了一種同樣的方法，並訴述了他的方法，它與我的方法幾乎沒什麼不同，除了他的措辭和符號以外“。但有趣的是，牛頓在第三版時候刪去了這一段話而希冀將微積分的功勞 記在自己名下。

關於《通報》的1672年內容。那個信中，牛頓慣用的隱匿了微積分的思想，很難從中看出微積分的思路。包括科林斯給萊布尼茲的信件中，微積分內容都很少，萊布尼茲只是得到了關於無窮級數的內容，而與微積分無關。

梳理完時間線，我們不難發現，萊布尼茲好奇的一直是二項式定理和級數展開，而對於他的整個微積分的體系來説，並不需要這兩個東西作為推論或者基礎，單純從信件角度來看，在1677年萊布尼茲完成了相關的微積分的基本體系的時候，和牛頓之間的交流也只限於二項式定理和級數展開。而且牛頓也在回信中，精心謹慎的迴避了微積分的方法，迴避了微積分而不直接講出來，將微積分藏了起來而並未告訴萊布尼茲。甚至將所有的微積分證明都使用了幾何證明而看不出微積分的痕跡。

而關於內容二，事實如下：

1676年5月12日，萊布尼茲的確還不知道如何推導sinx和arcsinx 的表達式，因此被人質疑，他1674年給出的π/4的級數展開是否有抄襲格雷戈裏之嫌。

格雷戈裏並不知道相關的微積分知識，而萊布尼茲是使用精妙的微積分進行計算得到的。（具體的π/4級數展開過程，我會附在附錄中以免影響文章的流暢性）“1674年不論是格雷戈裏還是惠更斯或者任何一個在巴黎的其他人，完全沒聽説過任何關於通過有理數的無窮級數來表示圓的面積的報道。“因此，可以説萊布尼茲的確是獨立的給出了萊布尼茲級數的推導而無抄襲之意。不過可惜的是，格雷戈裏幾年前實際就給出了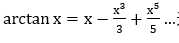這個表達式。而只需要將x=1代入其中就可以得到萊布尼茲級數，

可能是格雷戈裏沒有意識到這個表達式的意義和美感，並未作此數值代換，失去了一個命名級數的機會。

因此我們可以不難看出來，萊布尼茲的微積分工作和級數工作都是獨立完成的，而且是有着完整的知識鏈條，其微積分的建立邏輯我們已經説過，而這個書信往來的佐證則完全可以説明萊布尼茲微積分的誕生是一項獨立的工作，英國科學家為維護牛頓對萊布尼茲的毀謗是沒有任何意義的。

後續的紛爭：[20]

1684年，萊布尼茲發表了關於微積分的第一篇論文，並未提及任何關於牛頓的內容。

1687年，牛頓出版《自然哲學的數學原理》，誇讚了萊布尼茲的工作。在《原理》一書中，牛頓並未提及微積分內容，代之以較為嚴密的幾何證明

1693年3月萊布尼茲寫信給牛頓，討論了一些其他的牛頓研究內容如光學等，試圖恢復和牛頓的通信關係，二人關係並無惡化，萊布尼茲問候如下：to the celebrated Issac Newton Gottfried Wilhelm Leibniz cordial greeting（戈特弗裏德·威廉·萊布尼茨向著名的艾薩克·牛頓致以親切的問候）[見下圖]

1693年10月，牛頓回信：“My aim in these pages has been to give proof that I am your most sincere friend and that I value your friendship very highly. Farewell. Cambridge, 16/26 October 1693.“[19]（即：客套的説萊布尼茲是他最好的朋友）。書信往來説明二者關係還未破裂，二者”措辭依然禮貌，當然，在兩人的信中都沒有任何對於剽竊的憤怒和指責對方的意味“（語出《數學恩仇錄》）

1696年6月，約翰伯努利發問數學家關於“速降線“的問題，牛頓匿名回答並使用了微積分內容，但萊布尼茲在1699年把這個解法作為微積分的成功示範提出並暗示所有人（包括牛頓）使用了自己創立的微積分，讓牛頓看起來是個抄襲者。牛頓追隨者丟勒因此憤怒的指責萊布尼茲才是那個抄襲者，引發了另一次爭議

1703年，胡克去世，牛頓成為了皇家學會的主席，並發表了《論求積》這一篇論文，某種程度上，《論求積》是1676年給萊布尼茲的那封關於級數的信件的補充。

1708年10月，牛頓的追隨者凱爾發文攻擊萊布尼茲從1776年牛頓給他的那封信件中獲得了靈感，在1711年，萊布尼茲寫信給皇家學會，要求澄清事實。我們在上面已經説過，那封信正好是牛頓有意為之，隱匿了微積分的思想，這次對萊布尼茲的攻擊是荒誕可笑的。但皇家學會主席當時正是牛頓。

1713年，英國皇家學會發表《通報》稱萊布尼茲抄襲。然而通報中內容過於偏頗。

1716年，萊布尼茲去世，但牛頓並沒有結束對萊布尼茲的攻擊

1722年，牛頓出版《原理》的第二版，開頭增添了一部分書信往來和證據來説明牛頓和萊布尼茲的交鋒，並且牛頓刪減，增添了對自己有利的一些東西。

1728年．《原理》第三版，牛頓刪掉了所有關於萊布尼茲的內容，聲稱“第二發明者沒有任何權利“

b)     爭端趣事[21]

 牛頓早期成果在《無窮級數分析》中，但是隻是以手稿形式存在，由於牛頓本人似乎認為其發明“只屬於自己，而不屬於世界和柯西，甚至不屬於子孫後代”，或者為了修改自己的發現，還有出版社由於出版巴羅（牛頓老師）的數學類書籍而破產導致數學著作出版十分慎重的原因，牛頓選擇了隱匿自己的研究。從而沒有發表，導致了現在仍舊紛爭不斷（《數學恩仇錄》第二章）

牛頓在所有和數學家交談的信件中，都將自己的微積分隱匿不發，換用其他等價的方式説明，《原理》中簡單提到了微積分，而並未用微積分進行相關證明。在所有的牛頓1760-1780年間的信件往來中，凡是所有的詢問他任何涉及微積分意味的問題，牛頓都會聰明的靈巧的給出一個特殊的幾何回答而躲開微積分的內容，翻閲他的書信集《The Correspondence of Issac Newton》中，這一點尤為明顯，當時的風氣決定了將論文隱而不發這一個舉動。

 牛頓聲稱自己17世紀中期就使用點標註法，然而研究發現，17世紀90年代才開始使用（霍爾 1980年 第39頁和第187頁）牛頓也聲稱自己在1676年就寫下了求曲線所圍成的面積的論文，經考證，那篇論文實際作於1691年，在萊布尼茲發表論文後。（莫爾 1962年 第592-594頁）

三．總結

由前述可合理推斷胡克先於牛頓提出引力的平方反比律，但牛頓第一個完成了橢圓軌道和平方反比力關係的證明。故可以説胡克啓發促進了牛頓萬有引力的提出與證明。《原理》中完全不提胡克的貢獻較為不妥。

而在前述的和萊布尼茲的微積分的爭議中，我們可以很容易看出來，雖然萊布尼茲和牛頓有過多次關於數學的書信往來，可是我們不難看出來，萊布尼茲和他的討論止於級數，並且，牛頓有意的隱藏了自己的工作，以防萊布尼茲看到。另一方面，由於《通報》的團隊以牛頓為首，裏面內容參差不齊，未免有過分誇大牛頓之嫌。當然我們不能否認牛頓在微積分領域的傑出貢獻，但是將這個殊榮只給牛頓未免不妥，史料證明，萊布尼茲建立了更加完備更加先進的微積分，而牛頓並無明確的先於萊布尼茲的工作。因此，我們説，牛頓和萊布尼茲共同獨立的建立了微積分呢，《原理》中第二版抹黑第三版刪去萊布尼茲的做法有些欠妥。

 四．參考文獻

[1]《自然哲學之數學原理》(英)牛頓著; 王克迪譯. -北京: 北京大學出版社, 2006.1 ISBN 7-301-09551-1

[2] <The correspondence of Isaac Newton Ⅱ> P301

[3] 譚世復.有心力運動軌道封閉性與圓軌道穩定性討論[J].湖州師專學報,1995(06):32-37.

[4] <The correspondence of Isaac Newton Ⅱ> P309

[5] <The correspondence of Isaac Newton Ⅰ> P412

[6] <The correspondence of Isaac Newton Ⅰ> P416

[7] <The correspondence of Isaac Newton Ⅱ>P209

[8] <The correspondence of Isaac Newton Ⅱ>P18

[9] <The correspondence of Isaac Newton Ⅱ>P53

[10] <The correspondence of Isaac Newton Ⅰ>P313

[11]-[14]《數學恩仇錄》P68

[15-18] <The correspondence of Isaac Newton Ⅱ>

[19] <The correspondence of Isaac Newton |||>

[20-21]《數學恩仇錄》哈爾 赫爾曼

圖片來源：圖一來自 百度百科；圖二、三來自 超星網；圖四來自 化學網。圖五、六、七來自Historical Society of Pennsylvania Digital Library