學做家長｜記孩子的一次“1.5小時熬戰一道數學題”的經歷及其收穫_風聞

煩惱即菩提。

                        ——惠能《六祖壇經》

孩子的教育即家長的修行。

                        ——《學做家長》

原文鏈接：學做家長｜記孩子的一次“1.5小時熬戰一道數學題”的經歷及其收穫，兼論家長提升自我修養的必/重要性，附對該題的批判性分析

**按：**筆者在自己的孩子很小的時候就強烈地意識到，家長不僅僅是為人父母的一個身份，更是一個需要學習才能扮演好的角色。所有家長都非常關心孩子的教育，但絕大多數家長往往僅僅是基於身份、而極少基於角色去對待和施行孩子的教育。此言何意？簡單説，基於身份，就會將教育對象偏重於孩子，下意識地認為只有孩子需要學習，而自己就是個天然的施教者；而基於角色，就會意識到，孩子的教育不僅僅是孩子自己的事，不僅僅是孩子學習，作為家長更需要學習，學習如何做家長、做更好的家長。反應於現實實踐中會怎樣呢？打個比方，對於魚龍混雜的各種教育理念和產品服務，若僅僅基於身份，那就會滿足於做一個“知道分子”，這樣就會隨波逐流、就容易受裹挾；而如果基於角色，那就會努力學習成為一個“知識分子”，去識別真偽優劣，然後“擇其善者而從之”並持之以恆、久久為功（而非易受急功近利的誘惑），特立獨行。正是因為有這樣的認識，所以筆者自孩子兩三歲時就開始不斷地學習、思考、探索、實踐、反省，現在孩子上三年級了，總得來説，筆者對自己在孩子教育上的成果還是比較滿意的。有些經驗教訓和心得體會值得分享，故而新開一個專題，取名為“學做家長”，其主旨是“論‘合格家長’的‘自我修養’”。筆者認為，在當今時代，要想成為一個“合格家長”，就要努力學習提升“自我修養”，包括：人文素養、科學認知（注：指“關於科學的認知”，而不是指——當然也必定要包括一些——“各門具體學科的知識”）、性情涵養。你的孩子能否成為牛頓，你的肩膀有多高是關鍵之一。切勿誤解，這不是説你必須要有胡克一樣的科學知識。筆者認為，家庭教育的重點不在知識的教授，而在學習上的引導，這一點可參看拙文《以二年級女兒的一個獨立發現為指引得到可推導出九九乘法表的一組公式》文末的“附1：評論”和“附2：三句教”。所以，要想孩子能脱穎而出，隨波逐流和依賴於同質化的學校教育是希望渺茫的，因此家庭教育的質量能否出類拔萃就尤為重要。取法乎上，得乎其中。讓我們一起“學做家長”，努力學習全面提升自己的人文素養、科學認知、性情涵養，以與孩子更和諧地相處，以給予孩子更好的引導。

導讀：

這道數學題（三年級），孩子在上面磨了近一個半小時才豁然貫通，過程於我於孩子雖然都很煎熬（孩子屢次請求甚至哭求講解輔導均予婉拒），但結果很美好，孩子創造的這種“對列式進行釋義”以輔助思考的模式/形式非常棒，我認為值得在家長輔導（僅限於講一些普適性的思維方法）中推廣，甚至學校老師在教學中亦可借鑑。

孩子接連做出的兩個堪稱出奇離譜的錯誤作答也是非常有意義的，因為正是通過這兩個錯誤孩子才真切體會到有時做對了也是稀裏糊塗地做對的，並非真懂，而在出錯之後再自行想通了才是真的懂了。

並且，通過對孩子出錯原因的探察，我發現這道題的表述是不嚴謹、不精準的。所以，迅速理解“正確”題意並順利作答的孩子，不過是在慣常思維或做題經驗、解題套路下的“自行腦補”或“不求甚解”罷了；而如我的孩子的出錯，並非説明孩子表現得差，反而恰恰説明孩子表現得好。

2022年1月上旬某日（上學期末月即2021年12月下旬開始因疫情而居家隔離，學生在家上網課）孩子（三年級）在課後作業中碰上這樣一道數學題：

孩子與這道題熬戰了近一個半小時才豁然貫通，其間我也備受煎熬，慶幸的是，我堅持貫徹了自己的教育理念、守住了自己與孩子約定的原則、hold住了自己幾次瀕臨失控邊緣的情緒，而孩子也獲益良多。

其中甘苦，回味無窮，值得記錄下來，以備過段時間可與孩子“温故而知新”。同時，也是一個分享，希望能給現任家長和候任家長一些有益的鏡鑑和啓發。

一、這場熬戰的詳情回顧

孩子讀題後之初，可能對這個題設的表述有點懵，所以來諮詢我這題目啥意思。

【補充説明：對於孩子的課後作業，從孩子上幼兒園開始，我向孩子強調並與其約定的原則是“三不”即“不輔導、不檢查、不打卡（即拍照發班級各科的微信羣）”，作業由孩子自己獨立完成、檢查、訂正，偶爾我會抽檢。孩子幼兒園期間和未上託管的一年級我就一直這麼做的，與孩子相處甚歡（從來沒有“一輔導作業就雞飛狗跳”的情況，因為我根本就不輔導，而孩子的作業完成質量也很好，考試成績也相當不錯），與學校和老師也都相安無事（這裏要感謝老師的寬容，沒有找我們不在羣裏交作業的麻煩）。孩子從二年級上託管後，我跟帶班老師也強調了“三不”原則，但執行得不太好，因為我們這種情況是異類，老師總會隨大流地給孩子們檢查/批改作業，但幸好，老師反映，孩子的作業完成質量很好，犯錯極少。所以，像這道題這種還沒做就來請教的情況是極少發生的，故而我判斷可能是因為孩子對這個題設的表述有點犯懵。】

【補充説明：對於這次因疫情居家隔離而上網課的課後作業，我與孩子的約定是，英語作業做不做隨她意願，語文作業是要全做的，數學作業在作業少時就全做，在作業多時就由我勾選幾個題做一下，其它的題“讀做”即可。這道題就是某次作業中我勾選的題之一。“讀做”就是不用動筆寫，只要讀題然後在心裏思考一下怎麼做就行了，但碰上“讀做”拿不下的題，那就還是要動筆做一下。配合“讀作”的是我的隨機抽檢核查，所以孩子不會在這方面“耍滑頭”“鑽空子”。“讀做”的方式也是從孩子一年級開始就一直採用的。“讀做”的方式是我在復旦大學哲學院王德峯老師的講座中聽來的，其來源是王老師的一個同校的數學系的教授，説是“讀做”時就可以以輕鬆的心態並以審美的視角去鑑賞題目，判斷哪些題目出得高明，哪些題目出得爛，如果換成自己出題，會怎麼出。我覺得甚有道理，於是就跟孩子講清楚了“讀做”的來龍去脈及其道理，並允許她在作業繁多時啓用。】

我讀了題目後，感覺這題目也不難啊，就在心裏猜測孩子的理解究竟卡在哪兒了，但我一時不能確認。於是，我就問她自己是怎麼想的。

孩子考慮了大概一分鐘後説：

32乘以4等於128，128減去兩個邊長減80等於48，48是兩個寬，除以2等於24，就是一個寬的長度了。

（非她原話，只是大概意思，其中有算式在心算時得數還算錯了，但計算步驟大致不差。注意，我這裏用的詞是“計算步驟”而不是“思路”）

我一聽，好着呢，計算步驟（注意，我這裏用的詞是“計算步驟”而不是“思路”）大致不差啊。於是就“嗯”了一聲繼而説道：“那就做去吧。”

這一做，好嘛，出問題了竟然，而且是接連出錯甚至錯的離奇。

下圖的草稿記錄了所出的錯及其過程（其中，標號1的是後來在我拍照時她補寫的，這個錯是她直接在題目下作答時犯的）：

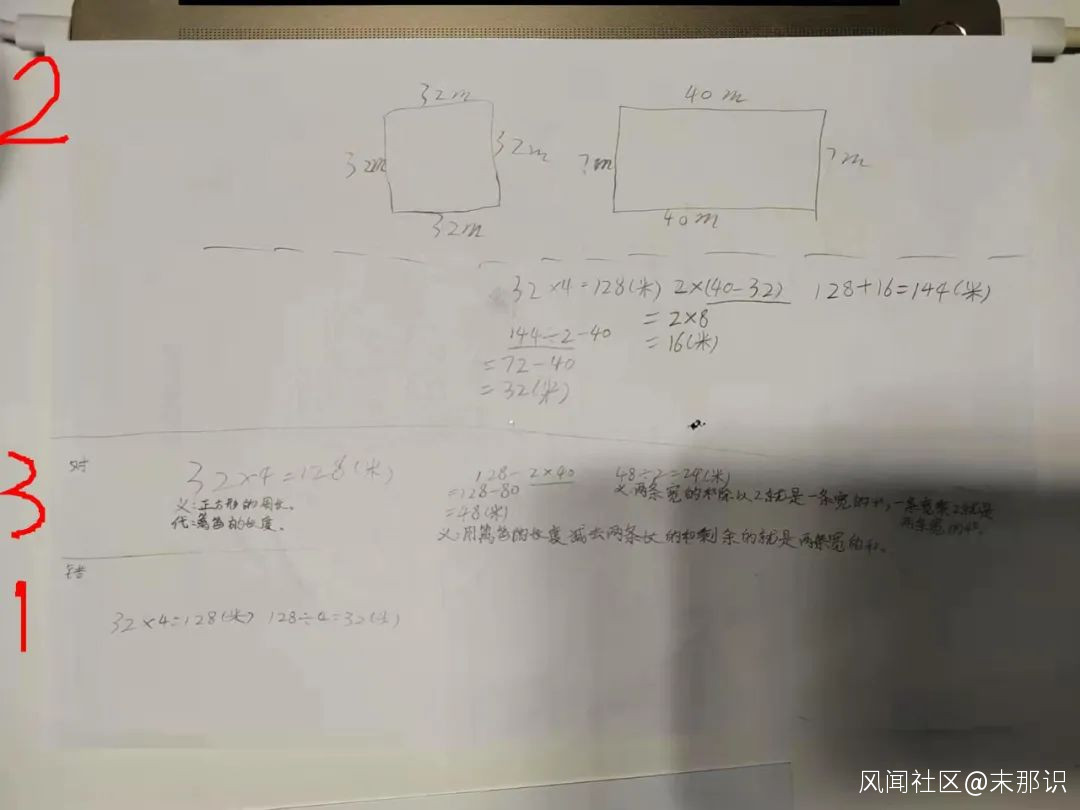
在我讓她去做後，她剛在課桌前坐下，還沒對題目作答時，她突然興奮地對我説：“爸爸，我想到了一個天才的解法。”我説：“哦~！那你寫來我看。”

標號1的作答就是她所謂“天才的解法”。

【補充説明：我一直有意識地培養孩子的“獨立之思想”，所以我經常鼓勵她要有自己的想法，並且經常以各領域的天才為例來説事論理，説得比較多的是科學史上的大咖的事蹟及其其中的道理。我還半嚴肅、半玩笑地經常稱呼孩子為“愛因斯坦·曦”。所以，孩子的思維確實比較活躍，也喜歡“胡思亂想”。故而，才有她在這道題上突發奇想，並自稱“天才的解法”。對於孩子的“胡思亂想”，我的原則是：其一，鼓勵鼓勵再鼓勵；其二，對於我自己能確鑿判斷為錯誤的想法及其指向的問題，我會循循善誘地帶孩子思考正確的想法；其三，對於我自己不能確鑿判斷正誤的想法及其指向的問題，我會介紹對這個問題我所知的已有的各派高人的想法，然後強調要孩子根據以後自己的學習體會去判斷；其四，對於據我所知還沒有人問過的問題，我會大加褒獎，並跟孩子説明，這個問題據我所知還沒人提出過，如果確實沒人想過這個問題，那你挖到寶藏了，解決了這個問題，你就是偉大的XXX家了。然後，就是順勢強調認真、刻苦學習重要性的説教了：你要想搞清楚並解決這個問題，你需要學習甲，需要學習乙，需要學習丙……】

我看了這個作答後，先是心裏偷笑了（這是啥啊，還“天才的想法”呢），然後穩住自己的心神，組織了一會兒自己的語言，繼而説道：

“第一，你這個作答不對啊；第二，即使是天才，有時也會想錯的，你這個小天才這會兒也想岔道了吧；第三，這跟你剛才跟我説的計算步驟也不一樣啊。你再仔細想想去吧。”

於是孩子繼續去想，想了幾分鐘，然後跟我説：“我剛才跟你説的計算步驟是咋説的呢？”

我説：“你自己去想。”

她於是又去想，想了幾分鐘，還是想不起來。於是又跟我説：“我之前跟你説的計算步驟到底是啥啊，你告訴我嘛！”

我説：“你想不起來，説明你之前是稀裏糊塗地對的，並沒有真正地弄懂。記得我跟你説過的嗎，‘明明白白地做錯了比稀裏糊塗地做對了更有價值’。所以，你不用去想你之前説的計算步驟是什麼，你就重新來思考這道題。”

【補充説明：“明明白白地做錯了比稀裏糊塗地做對了更有價值”這句話及其道理是我與孩子以前討論另一道題目時説過的。詳見文末“附文：數學題出題原則之我見”。】

於是，孩子又去想，但是還是不行（可能一時想不明白後就又去回想她初時跟我説的那個計算步驟是怎麼樣的，但回想不起來），於是又來問我，這次是哭求了。我依然不為所動，還是讓她忘了之前説的計算步驟重新去思考這道題。但是給了她一個建議，讓她將題目逐字逐句連讀10遍以好好理解題目的意思。

於是，孩子開讀。我聽她讀題的狀態，明顯有點小和尚唸經的味道。但我並沒有説破。

她讀完10遍後（是數着遍數的），説她讀完10遍了。我問那你讀明白題意了嗎，她説沒有。我説，讓你讀題10遍，你讀不是完成這個10遍的任務，而是要邊讀邊想以理解題意啊，你數着遍數讀説明你沒有認真去讀。然後讓她繼續讀題，但這次又給她加了個建議，讓她邊讀題邊畫圖去輔助思考和理解。

【補充説明：“圖解法”我之前教過她幾次，並建議要常用。我教的圖解法是：將題目中的每一句話都以圖示的形式表示出來，一為輔助理解和思考，二為避免犯“自以為是”（在所難免）的錯誤。】

於是，孩子又去想了，也畫了圖，並且作答了，見草稿照片中的標號2。

孩子拿來我一看：媽呀，這思路，都亂成一團麻了。趕緊穩住自己的心神和情緒後，我跟孩子説：“你這個有點想多了，想複雜了，或者想岔道了，從你這個作答中，能看出來你的思路亂得厲害，完全沒有理解題意。再去認真想想吧。”

我話音剛落，孩子就徹底崩潰了，哭了起來，哭得那叫一個傷心。

想想也是，孩子被這道題以及我（倔強地堅守原則）“折騰”了將近一個小時了，結果卻不僅沒鬧明白反而越來越迷亂，孩子肯定對自己有些沮喪、對我有些怨氣。

深呼吸，穩住自己的心神和情緒，先是插科打諢地逗了幾句，然後就是温柔地摟她在懷裏讓她哭了一會兒，再然後，就言歸正捲了。

先是安撫、開導。

我跟孩子説了兩點：其一，跟她説，“題目還得你自己去想明白，我不能講解，一講解你立刻且輕鬆地就明白了，但這不是你自己想明白的，所以其實你還不一定真的明白，這個道理就像我們玩的猜字謎，你自己一時半會兒猜不到然後非要我給提示，結果我一提示你就猜到了，但這不是你真的猜到的”；其二，跟她提起了《大學》中的“定、靜、安、慮”，意思是讓她調整好情緒，“定”心、“靜”心、“安”心，然後去“慮”——思考，才更能有“得”——想通、想明白。

孩子在我的安撫、開導下很快平靜了下來。

【補充説明：“其一”提到的“猜字謎”是我和孩子從她一年級逐漸認字起就開始的遊戲，其一大特點是所有謎面都是我自己構思、設計出來的。“其二”提到的“定、靜、安、慮”方能“得”的道理也是之前跟她講過幾次的，第一次講的契機是我在聽《大學》的相關講座時她好奇的問，我就講了“定、靜、安、慮”方能“得”的道理，並與她分享了我自己的親身經歷和體會，之後幾次講都是她自己處於相關情境中時，我跟她再講這個道理，她自己也實踐並有所得了，所以她還比較認可這個道理並有自己的體認。正是有之前我們這些溝通的基礎，所以孩子能很快平靜下來。】

於是我跟她説回到這道題。

我以分析她的思路為什麼錯亂的方式給她提了個建議，原話我記不太清了，大概意思是：你列的算式你自己要明白你要算什麼、算式中的每個數分別對應什麼、每個算符又是要幹什麼。

然後孩子就繼續去做了。這次孩子的狀態明顯就不一樣了，我的感覺就是“很安靜”，臉上也是一副認真思考的表情。

【補充説明：從幼兒園開始，孩子寫作業時，我總是離她遠遠的，並總是讓自己忙起來，這樣孩子想問也不方便，就只能自己思考、自己做。這次居家隔離期間也類似，我們各自做各自的書桌，相隔“遙遠”。所以，孩子的表情是我偷瞄到的。】

十幾分鍾後，她完成了這道題，就是草稿圖中的標號3的作答。

我一看，非常好，不僅三個算式都列對了，而且每個算式下面孩子還寫了對它們的釋義，並且語言通順清楚、釋義準確無誤。

當時的感覺是：煎熬，終於結束了！

於是，我將孩子大大褒獎了一番。

隨後，孩子將草稿上的正確作答寫到作業的題目下面就高高興興地玩去了。

事後，我跟孩子又對該題以及孩子當時的思考過程尤其是兩個錯誤作答究竟是怎麼想的、為什麼那麼想等細節做過多次討論，在這個猶如“破案”的多次討論中，我才終於弄明白了所有細節，孩子也從討論中獲益良多。

二、這場熬戰收穫的成果

1、孩子明白了做對了不代表真懂、做錯了不代表就笨甚至反而代表高明

做對了不代表真懂

小學數學的題目尤其是這類數學應用題，其作用不僅僅是考核孩子對具體數學知識的掌握情況，更是或者説更應該是——這要視出題人的數學修養（注意我説的不是數學知識及其技巧能力）而定——引導孩子對數學理念（數學的嚴謹性——體現在題目的表述中——和數學抽象的思維及其能力）的領會，同時要呵護好孩子在數學上的靈性——這就意味着出題本意不能走偏到為了考倒孩子而刻意設置不合理的障礙、甚至是惡意挖坑（關於這一點，這裏不展開，將另文討論）。

這道題

王大爺買了一些籬笆，計劃把邊長為32米的正方形菜園圍起來。如果這些籬笆也正好能把一個長40米的長方形菜地圍起來，這個長方形菜地的寬是多少米？

表面上看，難度不大，我也相信絕大部分孩子都能順利做對，但這不代表孩子真明白（猶如我的孩子在剛開始跟我口述時其計算步驟是對的，但動筆作答時又由於原有的初始疑慮“作妖”而逐漸陷入迷亂導致接連做出兩個出奇離譜的作答），或許連我的孩子最後想通時的那種明白程度（表現在孩子對各算式的釋義上）都沒有達到，遑論真懂了最應該懂的東西（主要指上文提到的“數學理念”，詳見後文的深入分析與討論）。

我的孩子經過了“從表面上的懂（口述計算步驟時是正確的）到發覺自己其實不明白（動筆作答時接連出錯）再到最後真的懂了”這樣一個過程，使她對“做對了不代表真的懂”再次有了切身體會（以前也有，這次更深刻），明白到不能止於“不求甚解”就得來的正確，而要做深度思考（當然了，要在力所能及範圍內）。

做錯了不代表就笨甚至反而代表高明

這道題：

王大爺買了一些籬笆，計劃把邊長為32米的正方形菜園圍起來。如果這些籬笆也正好能把一個長40米的長方形菜地圍起來，這個長方形菜地的寬是多少米？

應該説，其本身所表現出來的立意——無論是否出題人的本意——還是相當高明的，試作如下拆解：

相對比較簡單的，是所考核的知識點，即長方形和正方形的周長的概念及其相關計算；

相對較難一點的，是從題目對具體場景的文字描述中做數學抽象提煉出數學算式；

最難的一點在於，將分別經過數學抽象得到的長方形的周長與正方形的周長，再次通過對題目中的關鍵字詞的數學抽象，建立起數學上的“相等”關係（其實涉及到數學量的比較，即通過“甲與乙相等”和“乙與丙相等”得到“甲與丙相等”，即通過“甲=乙”和“乙=丙”得到“甲=丙”）。

然而，其表述卻存在兩大缺陷。

其一、不貼合現實。

其表現是，根本沒有給出一個現實且合理的説法來表述“正方形菜園的周長和長方形菜地的周長這兩者是相等的”這個關鍵數學關係。

其二、不嚴謹、不精準。

其表現是，有歧義或者説表述的指意是不明確的。

對這兩大缺陷的具體分析詳見文末所附“對該題的批判性分析”。

所以，絕大多數孩子的迅速理解“正確”題意並順利作答的表現，可能不過是在“慣常思維”或做題經驗、解題套路下的“自行腦補”或“不求甚解”罷了

而我的孩子之所以陷入迷亂並且錯得離奇，就是因為在上述“最難的一點”上產生了困惑，而產生困惑的原因卻是題目在表述上的上述“兩大缺陷”尤其是“其一”的缺陷。

所以，雖然我的孩子在這道題上出錯，但錯在“最難的一點”也是對學習數學來説最重要的一點上，而這一點恰恰又是體現孩子“數學靈性”和對數學的“直覺”的關鍵。此言何意？這個解釋起來比較費勁，總之是對習以為常的東西要保持一種直覺的批判性的“數學靈性”，而不為其所固化、桎梏，這是真正的創造力的源頭活水。想要深入瞭解的話，請參看如下兩篇文獻：

對1 + 1 = 2 的好奇心

構建數學和物理基礎的範疇論：用「等價」取代「相等」丨眾妙之門

順帶説一句，看這種文獻不是為了學習其中的具體知識以備去教孩子，而是如我在文首的“按”語中所説的，提升自己的“科學認知”，也就是擴展視野、提高見識、提升審美（判斷力），以更好的引導孩子，或至少，不至於成為誤導或絆腳石甚至劊子手。

如我的孩子在這道題上的經歷，算是因禍得福吧，體會了一番上文提到的“數學理念”。而這又得益於我的“科學認知”，否則我不會從這道題中深究出這麼多道理並在跟孩子的討論中引導孩子自己去領會，也不會不僅不批評孩子的出錯反而大讚錯得有價值，這樣既鼓勵了孩子敢於獨立思考而不怕犯錯的勇氣和精神，也呵護了孩子的“數學靈性”和“數學直覺”。

2、孩子在通過自己的獨立思考解決難題方面多了次經驗、增強了自信

“詳情回顧”中提到我和孩子自她識字起就經常玩猜字謎的遊戲，而且謎面都是我自己設計的，有時也讓她自己設計謎面讓我猜。

猜字謎的過程中，孩子體會到，有時對於一時猜不出的字謎，如果稍加提示，就能馬上猜出來。但這不是自己獨立猜出來的，也説明其中有關鍵環節自己沒有想通。

其實，孩子做題的道理也與此類似。家長稍加輔導，也許孩子就會做了，而其實，孩子可能沒有真的明白，自己也缺失了獨立思考解決疑難的經驗——這些通常是“默會知識”（用know-how或許更能清楚表達其意）。而欠缺了這些經驗，孩子在練習題中就會碰到更多一時想不通的疑難，然後慣性地依賴於求助家長或老師的講解。久而久之，孩子獨立思考勇氣和能力就降低了。

所以，關於作業，我跟孩子約定的原則就是“三不”（我對她的作業“不輔導”、“不檢查”、“不打卡”），自己獨立完成，遇到疑難自己思考解決，做完自己檢查，由於“不打卡”，所以若有題目當天想不通可以暫時放下、以後再補。

因此，我才會放任孩子在這道題上耗費近一個半小時，而且在她幾次請求甚至哭求講解時，我都堅決婉拒了。

這才使得孩子通過熬戰這道題在自己的獨立思考解決難題方面多了次經驗，同時也增強了自信。

3、孩子發明了一個值得推廣的“對列式進行釋義”的輔助思考的模式/形式

孩子最後的“正確”（若考慮到題目表述的不嚴謹、不精準，這個正確要加引號）作答如草稿照片中的標號3，為清晰顯示，另製圖如下：

看到這個作答，當時我就驚呆了！

孩子不僅做對了，而且創造了一個非常棒的輔助思考的模式/形式，即：

“對列式進行釋義”。

其背後的道理在於：當語言“通順”時，一般而言，算式就是對的並且思路也是對的；反之，算式就是錯的並且思路也是錯的，或者，即使算式是對的，但其實在思路上還是懵的——沒有真的想通。

雖然我在跟她分析她前幾個作答為什麼錯亂時説過這個大概意思，但孩子能迅速領會並將其落到實處且豐富了細節而形成書面形式，這就難能可貴了；尤其是，我馬上意識到，這種**“對列式進行釋義”**模式/形式孩子只要此後常用，對任何數學題基本都能無往不利；並且，我認為值得在家長輔導（僅限於講一些普適性的思維方法）中推廣，甚至學校老師在教學中亦可借鑑。

三、家長提升“自我修養”的必要性和重要性

看過“詳情回顧”當知，事中（孩子熬戰該題全程）我還沒發現題目表述是有問題的，所以也只是慣常思維下的去按套路理解題目，覺得題目不難。

諸君設身處地，如果你是我，你會在各個節點上有怎樣的反應或表現。

反正，老實説，雖然我自問在“性情涵養”方面的功力也有一定的火候，但是期間我也有幾次差點hold不住——或者答應孩子的請求/哭求給她講解算了、或者爆發怒火訓斥孩子（上演“一輔導作業就雞飛狗跳”的戲碼）。

如果禁不住孩子的請求/哭求而給孩子講解了題目或哪怕是稍加點撥一下，孩子雖然能迅速明白並正確作答，但其思考上的卡點可能並未得到解決，孩子也錯失了自己獨立思考並想通的機會，更不會有最後的“對列式進行釋義”這種輔助思考模式/形式的創造性發明。

如果對

孩子作答中的離奇錯誤

和/或其長時間都想不明白這道不太難的題目

和/或設若經過我們自認為嚴謹精細的講解後孩子還是一臉懵的“笨”樣兒

感到氣惱甚至憤怒繼而對孩子大發脾氣宣泄自己的情緒，那不僅是對孩子的情感上的傷害，更會讓我們在事後汗顏的是我們可能其實冤枉了孩子——因為孩子的不明白恰恰是因為ta們敏鋭地直覺到了題目表述的缺陷（導致孩子疑惑、迷亂之處）。

這個案例表明，“一輔導作業就雞飛狗跳”的病根可能不在孩子身上，而在家長自己身上，那就是家長的“自我修養”。

****從該案例中我們可以體會到，“合格家長”應該在“明理”（包括“人文素養”和“科學認知”兩方面）和“養性”（指“性情涵養”）兩方面具備一定的“自我修養”。

“明理”方面：

1、“一輔導作業就雞飛狗跳”的速效且正確的唯一解決之道就是堅決不輔導孩子的作業，小學階段的作業相對於現在這些小朋友的智力水平來説，真的沒什麼難的（數學院士看到都頭疼的愚蠢題目除外），只要靜下心來認真思考，都能獨立完成。所以，一定要相信孩子能行，對於作業可以堅決放手讓孩子自己獨立完成，必要時當婉拒孩子的輔導請求。小學養成習慣了，中學自然也不必輔導了，況且隨着孩子年級升高，即使你想輔導可能也有心無力了。

2、明明白白地做錯了比稀裏糊塗地做對了更有價值。做對了或許沒啥了不起，因為有可能是稀裏糊塗地的做對了，其實可能沒有真懂；而做錯了以後再去靜心思考然後想明白了那肯定就真懂了。所以，對於錯誤，不必苦惱，而應歡迎，因為錯誤是取得真正進步的階梯。

3、**思路清奇的錯誤相對於中規中矩的正確更有價值。**我們家長要守護孩子的靈性，只要是獨立思考所犯的錯誤，無論錯得多麼離奇，都要儘量先行肯定、鼓勵其獨立的思考（須知天才才會思路清奇故而難免犯錯多多天才經常是一天有十個新鮮想法但有九個半都是不靠譜的，但某天可能就有那半個靠譜的能生髮出偉大的成果）。因為，**獨立思考才能有所發明、創造。**我們家長不但要寬容孩子在獨立思考中所犯的錯誤，甚至要鼓勵孩子勇於犯錯的精神。

4、切忌“以己度娃”。人的思維的發展自有其年齡上的規律，並且，人的思維與其所學習積累得來的經驗是息息相關的。因為，人對世界的經驗其實就是語言的經驗（這個道理來自馬克思學説，但是否馬克思説的，我不確定）。不同年齡段的人，其語言經驗是不同的，年齡大的一般要更豐富一些，所以思維相對成熟一些。同為成人，不同的語言經驗也塑造不同的思維水平或思維方式，“隔行如隔山”、“不明覺厲”、“字都認識系列”（常見於大眾對科技論文或新聞報道的理解困難，每個字都認識，但不解詞意、句意、文意）這些俗話就印證了這個道理。所以，在輔導作業時，不要自以為是的以為自己的講解都多麼細緻、縝密、透徹了而孩子還是不明白就認為孩子怎麼這麼笨，而要充分認識並理解孩子自有孩子在理解能力上的侷限和難處，而你並沒有洞察到孩子思維、理解上的難點、卡點所在。

5、孩子身上的問題其根源出在家長這裏。按上述第4點的“語言經驗”之説，孩子在學校所得的語言經驗是基本相同的，唯一不同處在於在家庭所得的語言經驗。所以孩子如果思維混亂、理解困難，根源在家長，家長首先要自我批評——而不是先批評孩子，然後找到問題所在並予以改進。

6、沮喪、慌亂、焦躁、憤怒等情緒不僅於事無補，還會讓事情變得更糟糕，“定、靜、安、慮”方可“得”（見國學典籍《大學》：“知止而後有定，定而後能靜，靜而後能安，安而後能慮，慮而後能得”）。這一點，對於家長和孩子都適用。要好好跟孩子一起學習、領會其中精義，運用於實踐定會受用無窮。

“養性”方面：

1、去妄。去除自己的妄念，因為妄念是不如意的根源。

2、克己。剋制自己的情緒，因為情緒是亂分寸的根源。

“明理”與“養性”是“修養”的一體兩面，是互為表裏、相互促進的；“修養”要學習，“明理”是“學”，“養性”是“習”（即“實踐”），學而時習之。

附、對該題的批判性分析

原題照錄如下：

王大爺買了一些籬笆，計劃把邊長為32米的正方形菜園圍起來。如果這些籬笆也正好能把一個長40米的長方形菜地圍起來，這個長方形菜地的寬是多少米？

因何批判

詳情回顧的開頭我已説明，孩子剛開始來諮詢我“題意”而被我反問她自己怎麼想的時，她口述給出的計算步驟及其分步算式是正確的，只是隨後自她突發奇想想到一個“天才的解法”開始，她的思路逐漸偏離“正軌”（注意我加引號了）而陷入“迷途”，從她的作答來看，思路簡直錯亂得離譜出奇，甚至都看不明白。

那麼，問題來了：

問題一、孩子剛開始口述自己的理解時為什麼能給出正確的解法（計算步驟及其分步算式）？

問題二、既然她知道題目的解法（計算步驟及其分步算式）那又為什麼還要來諮詢我題意呢？

問題三、口述了正確解法但為什麼動筆作答時卻又接連出錯、而且錯得離譜甚至於看不明白其中的思路？

問題四、孩子最後的正確作答是因為想通了什麼也即導致她接連作答出錯的思路上的卡點或者説岔點究竟是什麼呢？

下面，我們對上述四大問題分別展開分析、討論。

對“問題一”的分析、討論

問題一、孩子剛開始口述自己的理解時為什麼能給出正確的解法（計算步驟及其分步算式）？

這道題，以我們家長/老師的眼光，初一看，不難，中間只轉了一個彎，題目的“題眼”是“也正好”三個字，這三個字相當於等式中的“=”，連接起了兩邊的算式即對第一句話作數學抽象得到的正方形的周長算式和對第二句話作數學抽象得到的長方形的周長算式。

相信絕大部分學生，在未及深思而僅略微思考一下（我這裏用詞很怪，不過看完後文你就明白了）就均能迅速準確的抓住這個“題眼”，然後按正確的計算步驟分別列出每一步的計算式，或者，僅僅根據做題經驗和思維慣性以及老師教過的解題套路，也能按正確的計算步驟分別列出每一步的計算式。

我孩子剛開始在向我口述的計算步驟也是正確的，但她屬於哪一種情況，我不太確定——即使在事後我們的討論中她説她後面思路錯亂的作答是因為沒有注意到“正好”這兩個字。

對“問題二”的分析、討論

問題二、既然她知道題目的解法（計算步驟及其分步算式）那又為什麼還要來諮詢我題意呢？

既然孩子剛開始是有自己對題意的一種理解並按其理解口述了對應的解法，那孩子為什麼還要來諮詢我題意呢？這説明孩子對自己的對題意的理解還不太確認。

為什麼孩子對自己的對題意的理解還不太確認呢？對這個疑問的解答才是搞清楚“問題三”和“問題四”的核心，也是解開“問題三”和“問題四”謎底的鑰匙。而對這個疑問的解答又與“問題五”直接、緊密相關。

可惜的是，我在孩子口述出了正確的解法後，以為她理解了題意，就沒有在意這個疑問；而在孩子隨後動筆作答接連出錯的過程中，我又簡單地以為孩子沒有理解題意或者是想多、想複雜了，從而忘了這個疑問。因此，實話説，孩子受的一個多小時的折騰有點冤屈，首要責任在“出題人”（這個疑問與“問題五”緊密相關），其次責任在我，所以我受的一個多小時的煎熬完全是咎由自取、一點都不冤屈。

我真正地徹底搞明白這個疑問，還是直到前幾天（好像是2022年2月16日）我和孩子再次對這道題的討論（因為要寫這篇文章，我跟孩子已經討論過多次，就想搞明白她當時思考中的細節），我忽然之間覺察到，原來這道題的表述是不嚴謹的，有歧義的，而正是這個“歧”，才讓孩子剛開始時對自己對題意的理解不太確認，也才讓孩子在動筆作答時接連出錯、而且錯的匪夷所思。這一點，詳見下文對“問題五”的討論。

對“問題三”的分析、討論

問題三、口述了正確解法但為什麼動筆作答時卻又接連出錯、而且錯得離譜甚至於看不明白其中的思路？

在事後我與孩子的多次討論中，我才搞明白她的兩個錯誤作答為什麼錯得匪夷所思以至於都看不出其中的思路。

孩子説，她那兩個錯誤作答依據的是對題意的如下理解：

將邊長為32米的正方形以其中一對邊不變、而另一對邊拉長為40米的方式拉伸得到一個長40米、寬32米的長方形。

正是基於如此理解，孩子的兩個錯誤作答就很好理解了：她已經從其對題意的理解中得知長方形的寬是32米了，相當於是“已知”的了；而兩個錯誤作答所列的算式，繞來繞去不過都是為了將要求解的長方形的寬算為32米，也即算不成32米她就下意識地以為算錯了，反正怎麼着都要將要求的長方形的寬算為32米；於是，標號1的錯誤作答——她自稱的所謂“天才的解法”——就看起來那麼好笑，簡直是“循環計算”，標號2的錯誤作答也是以先定的答案（即32米）為目標來湊算式，只不過是因為我建議她以圖解的方式去輔助思考，所以算式看起來比標號1的作答要複雜一些。

那麼，孩子對題意的上述理解又是從何而來呢或者説基於什麼呢？乍一看，似乎是毫無根據，是無中生有，甚至是簡直有點無厘頭。但孩子給出了她的這個理解的思考基點，即：

籬笆在圍起正方形菜園後是有富餘的，此時籬笆長度未定。

正是基於此點出發的思考，才將“正好”理解為全部籬笆（圍起正方形的和富餘的之和）的長度與長方形的周長相同，而這個長方形是將正方形以前述方式拉伸（寬不變仍為32米，長度拉長為40米）而得到的。

若不深入體察，會覺得這個思考基點仍然是毫無根據、無中生有、簡直無厘頭。但真的是這樣嗎？非也！詳見下文對“問題五”的討論。

對“問題四”的分析、討論

問題四、孩子最後的正確作答是因為想通了什麼也即導致她接連作答出錯的思路上的卡點或者説岔點究竟是什麼呢？

據孩子自己在事後我們的討論中所説，她是注意到了“正好”這兩個字，而前面兩個錯誤作答是忽視了“正好”這兩個字。

按照我前文對前三個問題的分析、討論，實際情況可能是：孩子之前對“正好”兩個字的理解有偏差——從“離題”的思考基點開始的想岔了道的理解，而最後的正確作答是“放下”（不再執着於）了這個理解偏差後迴歸到了對“正好”這兩個字的理解的“正軌”，也即是説，回到了“慣常”的理解模式，於是就做出了“慣常”的“正確”作答。

“改邪歸正”、終成正果，似乎很好嘛。但我以為，這仍然不究竟。為什麼這麼説，且看下文。

綜上所述，以上四個問題，如果我們只是從“做題者”的視角來分析，我們是無法得到一個縝密、自洽、合理的解釋的——雖然對單獨的每一個問題都似乎能給出合理的解釋；而只有從“出題者”（以審美/鑑賞）的視角來分析，我們方可將這四個問題納入一個解釋框架且其解釋縝密、自洽、合理。

從“出題者”的視角，我們就要再問一個問題：

問題五、這道題的表述是貼合實際並且嚴謹而無歧義的嗎？

如何批判

現在，我們以“出題者”的視角——以審美/鑑賞的眼光——來看這道題。

我們先再來認真閲讀一遍題目（我認為的關鍵字眼已加顏色標記）：

王大爺買了一些籬笆，計劃把邊長為32米的正方形菜園圍起來。如果這些籬笆也正好****能把一個長40米的長方形菜地圍起來，這個長方形菜地的寬是多少米？

應該説，其本身所表現出來的立意——無論是否出題人的本意——還是相當高明的，試作如下拆解：

相對比較簡單的，是所考核的知識點，即長方形和正方形的周長的概念及其相關計算；

相對較難一點的，是從題目對具體場景的文字描述中做數學抽象提煉出數學算式；

最難的一點在於，將分別經過數學抽象得到的長方形的周長與正方形的周長，再次通過對題目中的關鍵字詞的數學抽象，建立起數學上的“相等”關係（其實涉及到數學量的比較，即通過“甲與乙相等”和“乙與丙相等”得到“甲與丙相等”，即通過“甲=乙”和“乙=丙”得到“甲=丙”）。

然而，其表述卻存在兩大缺陷（拋棄成見——慣常思維下的“自行腦補”、“不求甚解”——然後稍作深思並推敲一番就不難發現）。

其一、不貼合現實。

其表現是，根本沒有給出一個現實且合理的説法來表述“正方形菜園的周長和長方形菜地的周長這兩者是相等的”這個關鍵數學關係。

於是，孩子就會很現實的想東想西（意欲腦補缺失的劇情細節）：

比如，王大爺買的籬笆到底是多長呢，不會那麼巧剛剛好圍起正方形菜園不短也不長吧（第一句話中用的是“計劃”二字，那所買的籬笆究竟是短缺了還是有富餘了，都不確定）；

再比如，王大爺是怎麼知道（以哪種方式或通過哪種途徑發現）圍起正方形菜園的籬笆也能正好圍起長方形菜園的呢；

還比如，計劃圍正方形菜園的籬笆怎麼就突然沒來由地跟長方形菜地扯上關係了呢——這到底是什麼不正常的關係啊；

等等。

其二、不嚴謹、不精準。

其表現是，有歧義或者説表述的指意是不明確的。

以下做詳細深入分析。 

1、這道題分為兩句話，兩句話之間的關聯是用籬笆的長度將正方形的周長和長方形的周長聯繫（注意，我這裏沒有用“相等”）起來，而表述這種聯繫的字詞是“也”和“正好”“能”。

2、從第一句話中，是不能確定買了的這“一些籬笆”究竟是多長的——雖然後面説了“把邊長為32米的正方形菜園圍起來”。因為這句話用的用於關聯的詞是“計劃”，而“計劃”在執行/落實後的結果有可能達成預期、也有可能達不成預期；也就是説，有可能所買的這“一些籬笆”的總長度不足以將正方形菜園圍起來、也有可能圍起來還有富餘。如果從這第一句話就理解出所買的這“一些籬笆”的總長度等於正方形周長，那恐怕是因為“自行腦補”或“自作多情”（因為是“計劃”而不是“剛好”）。

3、從第二句話中，我們可以確定“這些籬笆”的長度與長方形菜地的周長是相等的嗎？“能”只是一種“定性”表述而不是一種“定量”表述，代表的意思是“這些籬笆”的長度“不小於”長方形菜地的周長，“不小於”包括了“等於”和“大於”（“大於”即代表“這些籬笆”圍起長方形菜地後還有富餘）。那麼在“能”前面所加的“正好”兩個字是否就能將這個“能”所指代的意思嚴格確定為“等於”呢？這一點我也不太確定，只是直覺上感覺“未必”。從語義上來説，“正好”既可以理解為數量上的關聯，也可以理解為事務上的關聯——即這些用來圍正方形的籬笆“也可用於”圍長方形。當然，有人或許會認為，語義要在語境中確定，這是數學題，當然要以數學題的語境將這個“正好”理解為數量上的關聯了，這樣這個“正好”就表示“這些籬笆”的長度與長方形菜地的周長“正好”相等了。對於這個爭辯，我要説，請注意，這個題目的表述完全是生活場景化的，刻意迴避了數學化的表述，數學的內容是要從這個生活場景化的表述中抽象出來的，你之所以能輕鬆做到將出題人意欲考察的數學內容從中提取出來，那多半不是基於縝密的語義分析和數學抽象，而僅僅是基於慣性思維或者積累的做題經驗/套路（做題家、手孰而已）。

4、現在將兩句話連起來看。首先可以確定的是，第二句中的“這些籬笆”與第一句話中的“一些籬笆”是“等同”的（其實以集合論的觀點來看，也未必，但糾結這一點，顯得我有點無事生非了，權且不論）。“也”字在這裏起什麼作用呢？從語文的角度看，去掉這個“也”字，句子的意思是一樣的，因為“這些籬笆”與“一些籬笆”足以表達其意，加個“也”字屬於重複性表達；即使我這個分析是錯的，但至少是個真實的感覺，孩子們也會有這樣的直覺的，這就足以誤導孩子出現理解偏差；但這個問題不是數學問題，而是一個語文問題，而且是這個年齡段的孩子還不具備應對能力的語文問題。但這個“也”字在出題人的本意中應該是聯結前後兩句話中相關數量關係的不可或缺關鍵詞，那麼我們再來看看即使按出題人的本意，其表述能否精確表達其本意。在句子中，“也”是與“正好”、“能”連在一起的，那麼我們看看“也正好能”這個表述。“也正好能”至少可以有三個理解：“正好也能”，“也正好”“能”，“也能正好”。前兩個理解的表述其實屬於一種，因為其其重心都在“能”，“正好也”和“也正好”是修飾語，這種表述所能表達的意思在上述第3點中我們已經分析過，是不確定的——表達的意思不唯一且數量關係不確定。只有第三個表述“也能正好”表達的意思是唯一的、數量關係確定的，能精準表達出題人的本意。

【補充説明：這裏的分析涉及到語言學上的“能指”與“所指”的概念。“能指”就是一個表述能夠表達/指向的意思，通常有多個；“所指”就是一個表述在具體的語境中所特定表達/指向的某一個意思】

分析完畢（有不盡之處請參考下文我對這道題的表述的各種修改方案）。

所以，絕大多數孩子的迅速理解“正確”題意並順利作答的表現，可能不過是在“慣常思維”或做題經驗、解題套路下的“自行腦補”或“不求甚解”罷了。

而我的孩子之所以陷入迷亂並且錯得離奇，就是因為在上述“最難的一點”上產生了困惑，而產生困惑的原因卻是題目在表述上的上述“兩大缺陷”尤其是“其一”的缺陷。

破而後立

那麼，這道題

王大爺買了一些籬笆，計劃把邊長為32米的正方形菜園圍起來。如果這些籬笆也正好能把一個長40米的長方形菜地圍起來，這個長方形菜地的寬是多少米？

應該怎麼表述才更好呢？以下是我的嘗試。

如果要讓表述最符合實際場景，那就要在表述結構上做大的修改。

比如：

王大爺買了一些籬笆，把邊長為32米的正方形菜園圍了起來，後來又將它們拆下來圍一個長方形的菜地，也能正好圍起來。如果這個長方形菜地的長是40米，那麼它的寬是多少米？

或者：

王大爺買了一些籬笆先後用來圍過兩塊菜園，發現圍起一塊正方形菜園的籬笆也能正好將一塊長方形菜園圍起來。已知正方形菜園的邊長為32米，長方形菜園的長為40米。問：這個長方形菜園的寬是多少米？

如果保持原題的表述結構，那隻要稍微調整即可。

比如：

王大爺買了一些籬笆，計劃把邊長為32米的正方形菜園圍起來。如果圍起正方形菜園的這些籬笆也能正好把一個長40米的長方形菜地圍起來，這個長方形菜地的寬是多少米？

或者：

王大爺買了一些籬笆，剛好能把邊長為32米的正方形菜園圍起來。如果這些籬笆也剛好能把一個長40米的長方形菜地圍起來，這個長方形菜地的寬是多少米？

或者：

王大爺用籬笆把邊長為32米的正方形菜園圍了起來，如果這些籬笆也能剛好把一個長40米的長方形菜地圍起來，這個長方形菜地的寬是多少米？

餘不盡述。