探索規律性_風聞
code2Real-有人就有江湖,有code就有bug2022-03-16 17:11
什麼是研究
1968年,科學家做了一個老鼠烏托邦實驗,把四對老鼠放在一個大籠子裏,有充足的食物和水,有人定期打掃,想看看老鼠能繁殖到什麼數量。
籠子的大小足夠3840只老鼠生活,但是實驗表明,200天后,老鼠數量達到一個拐點,開始爆炸性增長,每55天增長1倍。等老鼠數量增加到640只時,增長率降低到每145天翻一倍。等到老鼠數量達到2200只時,老鼠數量幾乎飽和了,過一段時間後,老鼠數量急劇下降低,只用了100多天,老鼠數量就減少到個位數。到930天時,最後一隻老鼠出生,之後不再有新的老鼠出生,到1780天,最後一隻老鼠死亡。
對這個實驗結果的解讀多種多樣,似乎有一隻無形的手在控制生物種羣的數量。
有一個教授有不同的想法,他將自己的學生分成多個小組。
小組之間競爭,以探索提高老鼠數量方法。
學生八仙過海,各顯其能,其中,老鼠數量最高的小組獲得了一等獎。
但是,教授意外地發現一個小組劍走偏鋒,發現了老鼠繁殖的規律性因素,因而獲得了特等獎。
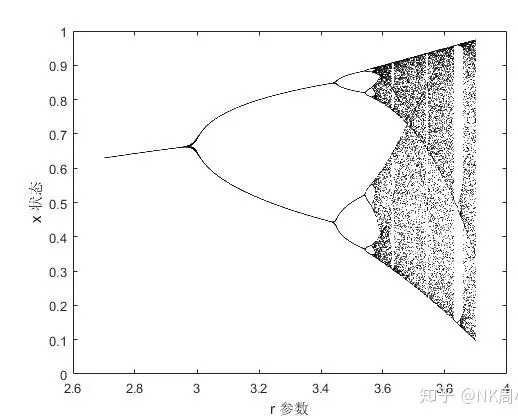
根據繁殖率公式,子代的數量x(n+1)=r*x(n)。
其中r是繁殖係數。
老鼠數量達到一個數值後變化比較穩定,被稱為達到均衡點。
當r<1,意味着數量減少,均衡點必然減少到零。這很容易理解:大家不婚不育,人類自然會滅絕。
當r>1,數量會開始增加,但是受環境影響會到達均衡點,形成一條水平線。
當r>2,均衡點不是一條直線,而是上下震盪,在相圖中表示為分叉,
當r>3,均勻點進一步分叉……
最後,學生髮現,繁殖係數與均衡點的關係很象混沌分形圖。
分型係數與費根鮑姆常數相關。
混沌分形結構可以放大,放大後局部與整體相似。再怎麼放大,都會發現它是越分叉越快的。而且後一級分叉比前一級分叉快的速度,趨近於一個常數,這個數就叫費根鮑姆常數δ=4.669201609102990671853203820466201617258185577475768632745651343004134.…
獲得一等獎的小組,相當於中國古代的科學研究,中國古代幾千年的科技發展,大多是在解決具體問題,對找規律性的東西並不上心。當然中國數學缺少形式化工具,很少有費根鮑姆之類的公式,因此難以上升到一般規律。
而獲得特等獎的小組,也許並沒有解決提高繁殖數量的方法,但是發現了更一般的規律,這個規律的發現在於小組有一定數學基礎。
歷史上,很多人能解決具體問題,但數學好的人能上升到理論,比如麥克斯韋因為數學好,總結出電磁理論公式,推動光電技術發展。
這種探索是我們工程人員所缺少的。