龐加萊的狹義相對論之一：洛倫茲羣的發現_風聞

對大多人而言，麥克斯韋最偉大的成就是統一了光學與電磁學。然而，他留下的這個領域遠非完美，諸多疑惑尚待澄清，比如光的色散、磁光效應，特別是運動物體的光學現象等，都沒有電磁解釋。針對這些問題，洛倫茲提出了他的電子理論，並在同期的眾多理論中脱穎而出。洛倫茲的座標變換、局域時間、對應態、長度收縮以及質量的速度依賴公式等新想法和新概念，直接導致了狹義相對論的誕生。正是在這樣的背景下，龐加萊和愛因斯坦於1905年分別獨立地提出了狹義相對論。本文通過歷史回顧和文獻綜述，希望得到如下基本結論：(1)假設(也僅僅是假設)要頒一個有關狹義相對論的諾貝爾物理學獎，那麼洛倫茲、龐加萊和愛因斯坦當之無愧；(2)假設只有一個人的名字可以用來冠名狹義相對論，那麼龐加萊比愛因斯坦更有資格獲得這個殊榮，也就是説，我們應該稱它為龐加萊的狹義相對論；(3)最合理的當然是，我們應該把狹義相對論稱為龐加萊—愛因斯坦狹義相對論。

撰文 | 金曉峯（復旦大學物理學系）

來源 | 本文選自《物理》2022年第3期

“不會又是標題黨吧？我們只聽説過愛因斯坦的狹義相對論，從沒聽説過什麼龐加萊的狹義相對論！”無論在物理圈內還是圈外，產生同樣的疑惑一點也不奇怪，即使是筆者自己，一年半前如果看到這樣的題目，也會這樣想。那麼，這一百八十度的轉變是怎麼發生的呢？原因很簡單，是下面這兩本書特別是第二本顛覆了我原來的想法：(1) O. Darrigol的《從安培到愛因斯坦的電動力學》[1]，(2) A. A. Logunov的《亨利·龐加萊與相對論》[2]。前一本書及其參考文獻比較詳細地介紹了龐加萊 (圖1) 在狹義相對論上的早期歷史貢獻 (1905年之前)；後一本書，特別是Logunov對龐加萊原始文章的導讀 (圖2)[3]，令人信服地證明：龐加萊在1905年已完整地建立了狹義相對論的全部基本內容。

圖1 龐加萊 (Henri Poincaré，1854—1912)

正是由於這一轉變，才有了2020年10月16日在復旦大學物理系教師午餐沙龍上的報告：“通往狹義相對論之路——對亨利·龐加萊遲到的致敬”。因為“蔻享科學”平台在網上進行了直播[4]，所以除了現場討論之外，會後還收到不少反饋。其中，有朋友建議，是否能將口頭報告轉換成書面文字，正式在中文期刊上發表。然而，由於這個問題的複雜性和敏感性，從口頭報告變成書面語言，意味着繁重的艱苦勞動。經過一年多的猶豫，最終還是下定決心花點力氣把它寫下來，供同行們批評指正。一年前為口頭報告準備的摘要，加了最後一句，直接移作了本文的摘要。

圖2 Logunov著書On the articles by Henri Poincaré《On the dynamics of the electron》對龐加萊原始文章做導讀

1921年，21歲的泡利在其名著《相對論》[5]的開篇“歷史背景 (洛倫茲、龐加萊、愛因斯坦) ”中這樣説：

“現在我們來討論洛倫茲、龐加萊和愛因斯坦的貢獻，它們包含了構成相對論基礎的推理線索和發展過程。從時間上説，洛倫茲是第一個，他證明了無源麥克斯韋方程組在下列座標變換下的協變性：

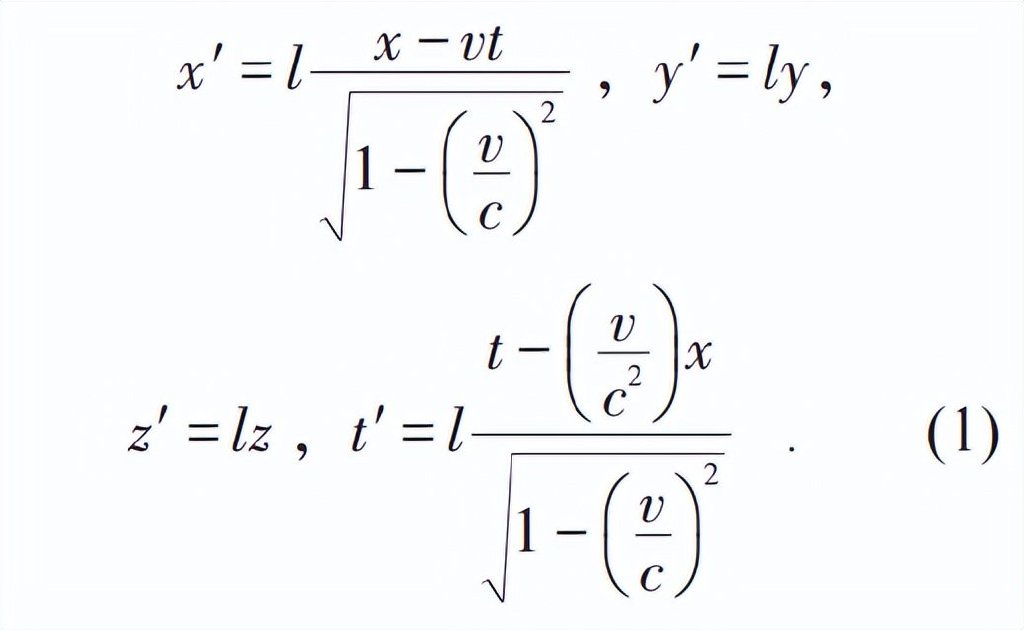(筆者注：這裏的l 是v 的函數l (v ))……我們應該強調指出，相對性原理，對於洛倫茲來説是陌生的。洛倫茲工作留下的一些不足，由龐加萊補上了。龐加萊聲明，相對性原理是普適且嚴格有效的。……他進一步糾正了在有電荷密度和電流存在情況下洛倫茲公式的錯誤，從而得到了有源麥克斯韋方程組的完全協變性。……最終，正是愛因斯坦，他完成了這個新領域的基本理論構造……他1905年的文章不僅包含了前面兩人的主要結果，而且展示了對整個問題全新的、深刻得多的理解。”

1955年，為紀念相對論誕生50週年，此時已55歲的泡利寫了一篇《相對論與科學》的小文章[6]，其中他這樣説：

“狹義相對論與數學中羣的概念密切相關，若説在伽利略和牛頓的力學中只是初見端倪，那麼現在已被實驗事實牢固確立起來了。……19世紀電動力學的發展以麥克斯韋和洛倫茲的一組偏微分方程組而告終。很顯然，這組方程不具備以前經典力學羣的對稱性……。現在的問題是：自然定律具有羣的對稱性這一説法，只是近似成立的性質而必須拋棄呢，還是經典力學的羣或許只是近似有效，而應該被一個更普遍的羣所替代，它同時對經典力學和電動力學都成立？最終的決定傾向於第二種選擇。這個假設可由兩條路徑來達到。一條是用純數學的方法，考察什麼是麥克斯韋—洛倫茲方程組協變性所滿足的最一般的變換羣，這是數學家龐加萊的途徑。另一條是通過批判性分析，來確定那些導致伽利略和牛頓力學所採用的那種特殊羣的物理假定，這是愛因斯坦的途徑。……愛因斯坦和龐加萊的結果都基於洛倫茲的前期工作，他已經相當接近但未真正達到最後結果。從愛因斯坦和龐加萊各自獨立的殊途同歸，我體認到了數學方法與(基於物理經驗基本特徵的)思想實驗(Gedankenexperimente) 之間和諧的更深層次意義。”

比較上面兩段泡利在21歲和55歲時，對同一事件所寫下的不同評價很重要，至少值得注意。很顯然，之前他將龐加萊與洛倫茲並列，而突出愛因斯坦的貢獻；之後他將龐加萊與愛因斯坦並列，指出他們倆都基於洛倫茲的前期工作，但從兩條不同的途徑，殊途同歸地達到了狹義相對論 (圖3)。愛因斯坦的狹義相對論已廣為人知，而龐加萊的狹義相對論卻鮮為人知。甚至在公眾認知領域給人們留下了一個錯覺，即沒有愛因斯坦，就沒有狹義相對論的誕生。這顯然與歷史事實不符。因此，讓更多人瞭解龐加萊的狹義相對論就顯得很有必要。

圖3 1911年，洛倫茲、龐加萊、愛因斯坦在第一屆索爾維會議上的合影

一個不得不問的問題是：如果龐加萊真的對狹義相對論做出了這麼大貢獻，那他的名字怎麼可能會在如此眾多的涉及相對論的現代教科書和專著中消失得無影無蹤呢？顯然，除了介紹龐加萊的狹義相對論，筆者還必須回答這個無法迴避的問題。造成這一世紀級現象的原因貌似千頭萬緒、錯綜複雜，實際上卻也簡單到用一句話就可完全概括：事實上，不是歷史對龐加萊開了一個玩笑，恰恰相反，是龐加萊對歷史開了一個玩笑！接下來，我們將儘可能把整個故事的輪廓梳理清楚，通過龐加萊所開的一個個生動“玩笑”，一起領略他做學問的獨特方式和他的科學哲學，一起景仰他的高貴人品。

1 龐加萊的兩個“玩笑”

龐加萊有關相對論的第一篇文章於1905年6月5日發表，一個月之後的7月23日又投寄了第二篇文章(圖4) [7] (愛因斯坦的三篇狹義相對論文章分別投寄於1905年6月30日、9月27日和1906年5月17日)，其中第一篇可以看成是第二篇的詳細摘要或總結，我們接下來以《六月文章》和《七月文章》分別稱之。龐加萊對歷史開的第一個“玩笑”出現在這兩篇文章的引言中。以後我們還會看到，這並不是龐加萊第一次也不是唯一的一次這麼做。因為他覺得自己的這項工作是直接受到洛倫茲1904年文章啓發而開展的，所以直至生命的終點，他都始終將狹義相對論的主要榮譽 (credit) 歸功於洛倫茲，哪怕一些完全是他自己原創的想法和貢獻也毫不例外，幾乎全部算到洛倫茲頭上。不得不説，這“玩笑”確實開得太大了，因為它給後人留下了極大的錯覺，似乎龐加萊在物理上沒有提出什麼新東西，只是在數學上提供了一些細節。不止於此，更糟的是，龐加萊與洛倫茲在許多關鍵點上的想法實際上很不一樣，甚至恰恰相反，比如，如何看待相對性原理、局域時間、以太等多個重要物理概念，而從今天的角度看，龐加萊是對的，洛倫茲是錯的，但因為龐加萊過世較早 (1912年)，而洛倫茲又是一個極其坦誠且從不羞於承認自己錯誤的人，所以我們今天所熟知的洛倫茲在相對論上的一些錯誤認識，反而都被後人轉嫁到了龐加萊頭上。這麼一來，本來極其簡單而清晰的歷史問題，頓時變得千頭萬緒、錯綜複雜。公平地説，這個“玩笑”絕不是歷史對龐加萊開的，而恰恰是他自己對歷史開的。

圖4 龐加萊有關相對論的兩篇文章

下面，我們來具體看看龐加萊的引言是如何寫的。在《六月文章》的引言中，他首先闡明一個實驗事實：所有試圖測量地球相對於以太運動的實驗 (包括邁克耳孫實驗) 都以失敗而告終；接着他説：

“不可能從實驗上揭示地球的絕對運動似乎應該是大自然的一條普適定律。……洛倫茲嘗試補充和修改之前所作的假定，用以解釋這種不可能性，並在他1904年《小於光速的動系電磁現象》文章中獲得成功[8]。這個問題的重要性促使我再一次回過頭來考慮它；我這裏所得的結果，在所有主要點上都與洛倫茲的結果相吻合，我只是嘗試着稍作改進，並提供一些細節。” “這些(與洛倫茲結果的)差別又都不太重要 (minor importance)，接下來會在後面的章節中加以展示。” (筆者注：後一句話為《七月文章》所加)

不知讀者看到上面加黑的句子是什麼感覺，筆者每次讀到這裏總禁不住感慨萬千！試想：假如我們今天的學術論文引言這樣寫，而且還想在國際主要學術期刊，比如《物理評論通訊》(PRL)上發表，哪有一個編輯會送審呢？這不是成心與自己過意不去嘛！且慢，這還不是最搞笑的，下面這兩段才真叫人啼笑皆非：

“洛倫茲的基本想法在於，電磁場的方程組在(1)式的變換 (我把它稱作洛倫茲變換) 下，將保持不變。” (《六月文章》)

“洛倫茲的概念，因此可以這樣總結：如果賦予整個系統一個共同的平移運動而可觀察現象沒有任何變化，那就説明，電磁場的方程在某個變換(我們稱之為洛倫茲變換)下是不變的。如此一來，這兩個系統，其中一個不動，另一個作平移運動，將互為完全相同的影像(become exact images of each other)”(《七月文章》)

事實上，在龐加萊之前，洛倫茲從來沒有這樣的想法，也從來沒有這樣的概念，更沒有如此説過！在這裏，龐加萊完全是將自己的原創性想法歸功於洛倫茲！對龐加萊而言，這並不是一時興起的偶爾為之，他始終對啓發自己想法的人心懷感激，之後總會在各種場合以各種方式加以強調；反過來，為自己去力爭優先權，對龐加萊而言卻是完全陌生的。好在洛倫茲也是一個對個人優先權毫不在乎的真正謙謙君子，他在《龐加萊的兩篇數學物理文章》[9]中如此實話實説：

“(龐加萊《七月文章》的)公式(4)和(7)在我的1904年文章中是沒有的，我甚至不知道存在一種直接的路徑導出它們，因為我認為(x，y，z，t )和(x ′，y ′，z ′，t ′)這兩個參照系存在本質差別。這是我當時的思路：其中一個參照系的座標軸是固定在以太中的，那裏有真實的時間；而在另一個參照系中，恰恰相反，我們只涉及(deal with)一些為數學技巧而引進的輔助量。……因此，比如變量t ′不能被看作是與變量t相同意義上的時間。在這樣的考慮下，我完全沒有意願按(x，y，z，t )參照系中描述現象的方式去描述(x ′，y ′，z ′，t ′)參照系中的現象。……我沒能證明麥克斯韋方程組的完全協變性；我的公式中還存留了一些本應消失的累贅項，只是它們在數量上很小而不會影響現象，我就是據此來解釋地球的運動不會影響實驗的觀察，但是我沒有建立起作為嚴格而普適真理的相對性原理。恰好相反，龐加萊證明了電動力學方程的完全協變性，並準確表達了“相對性假定”——一個由他引入的術語。事實是，正是採用了我沒能想到的觀點，他導出了公式(4)和公式(7)。還應該補充一點，在糾正我工作中的那些缺陷時，他從未有過任何對我的責備。”

龐加萊的第二個“玩笑”，開在對《七月文章》正文的章節安排上。《七月文章》除引言外還有9個帶標題的小節，其中，他竟然把自己在相對論中最重要、影響最深遠、也最能體現他遠超洛倫茲的原創貢獻，放在第4節而不是第1節，並且冠以“4.洛倫茲羣”的標題。前三節的標題分別是“1.洛倫茲變換”，“2.最小作用量原理”，“3.洛倫茲變換與最小作用量原理”；只要細心研讀過《六月文章》和《七月文章》的人，一定不難發現，龐加萊如此安排的唯一目的，就是為了突出洛倫茲的功績，而不想以自己的工作來喧賓奪主。從今天的角度回頭看，這個“玩笑”開得太大、後果太嚴重了。因為李羣和李代數對當時的大多數學家而言，也是新鮮且抽象的理論，對當年的物理學家來説，當然實在太超前、太高深了，幾乎無人能懂，所以如果放在第1節，至少能讓人知道這是全文的基礎，引起人們的重視；但現在放在了第4節，確實與第3節和第5節的內容上下不搭，除了知道洛倫茲變換構成一個羣外，別的似乎都是一些不知所云的數學細節；無疑，這種“奇怪的”章節安排，客觀上確實嚴重阻礙了龐加萊的相對論在物理學界的傳播。否則，他對狹義相對論的原創性貢獻，無論如何也不會被同代和後代人誤讀。另外，因為略去了太多具體數學推導和物理文字説明，以至於半個世紀之後，當龐加萊法文的《七月文章》被翻譯成英文時，還發生了譯者面對整個第4節中最重要的一句話——“我們也可以用另一種方式產生這個羣 (Nous pouvons encore engender notre groups d’une autre manière) ”，一定完全不知所云，竟然乾脆刪去不譯的尷尬局面[10,11]！

2 洛倫茲羣的發現：歸納的一步

關於“洛倫茲羣”的重要性，大概沒有比愛因斯坦1950年為《科學美國人》所寫《論引力的廣義理論》(On the generalized theory of gravitation) 中的這一段話講得更透徹、更深刻的了：

“麥克斯韋方程組暗示(imply)了洛倫茲羣，但洛倫茲羣並不暗示麥克斯韋方程組。洛倫茲羣也許確實可以獨立於麥克斯韋方程組，而被定義成這樣一組線性變換，它確保一個特殊的速度——光速——不變。這一組變換適用於從一個“慣性系”到另一個與之勻速運動的“慣性系”的轉變。這個變換羣最引人注目的新奇特性在於，空間上異地事件的同時性概念消失了。這樣，所有的物理學方程在洛倫茲變換下協變就順理成章了(狹義相對論)。事情就是這樣，麥克斯韋方程組導致了一個啓發性原理(heuristic principle)，它的有效性遠遠超出了方程組本身之應用甚至成立範圍。”

鑑於洛倫茲羣對整個基礎物理學的極端重要性，或許將第4節原文——難得一見的科學藝術品——直接附上會受到讀者的歡迎 (圖5)。

圖5 龐加萊《七月文章》的第4節

雖然沃伊特 (Voigt) 在1887年、拉莫爾 (Larmor) 在1900年都分別得到過類似於(1)式的變換式，但確實是洛倫茲1904年的結果，直接催生了龐加萊狹義相對論的誕生。無論是Voigt、Larmor還是洛倫茲，在得到他們的變換式時，具體思路可能各不相同，但一個共同的特點是，全都採用了特設 (ad hoc) 方式。作為大數學家和大數學物理學家，龐加萊顯然比任何人都明白，如此重要的變換式必定存在一個更本質的原理式基礎，而這正是他在《七月文章》“4.洛倫茲羣”這一節成功奠定的。簡而言之，他是通過歸納的一步和演繹的一步達到了這一目的，讓洛倫茲變換式(1)從此擺脱了特設的歷史，正式建立在堅實的原理之上，進而一舉奠定整個狹義相對論的數學和物理基礎。值得強調，龐加萊的這兩步——歸納與演繹——事實上正是對應了上述愛因斯坦的兩句話“麥克斯韋方程組暗示了洛倫茲羣，但洛倫茲羣並不暗示麥克斯韋方程組。

龐加萊證明：以特設方式得到的洛倫茲變換式(1)構成了一個羣；事實上，他也只證了關鍵一環，即羣的封閉性 (其餘的太顯然了！)。雖然從今天的角度看，這個貢獻似乎不值一提，因為基礎稍好的本科生就能做到，但在當時，世界上恐怕還真沒幾個人明白龐加萊究竟在幹什麼，因為對於物理學家來説，不僅羣論是陌生的，而且全新的速度相加公式 (今天被稱為愛因斯坦速度相加公式) 更是聞所未聞(他在第1節中，只用一行數學推導就嚴格證明了)。有點諷刺的是，這個在現代教科書上常常被認為“很相對論”的重要公式，龐加萊連個公式編號都沒給。

龐加萊進一步闡明，洛倫茲變換式(1)構成的羣是一個叫李羣 (Lie group) 的連續羣。李羣有一個重要特性：整個羣的性質可以由不變元附近的羣元性質完全確定，即Sophus Lie發展起來的無窮小生成元概念。這就是接下來龐加萊為什麼要取l=1，又假設δv/c≪1為無窮小，從而將(1)式轉換成在不變元(v=0)附近的變換式(2)來展開討論的道理：

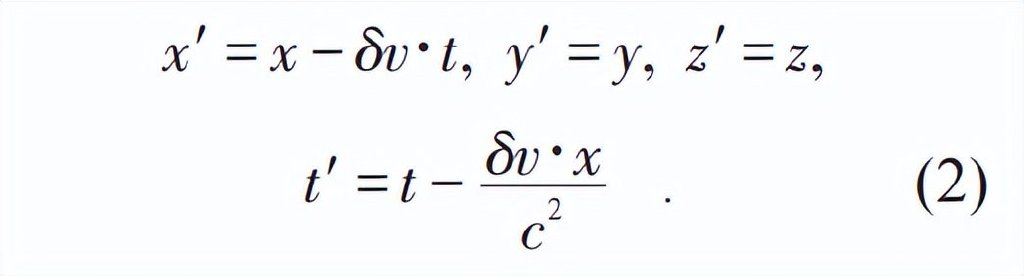他指出，這個變換對應於李代數中的

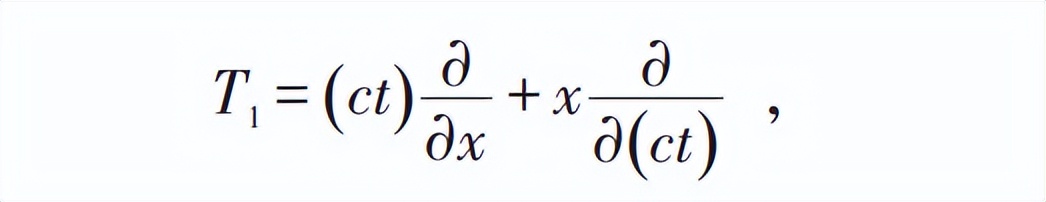相當於沿垂直於x-t 平面的一個無窮小定軸轉動。另一方面，從純數學的角度看，也可以取v=0，同時讓l有一個無窮小變化l=1+δl，這樣

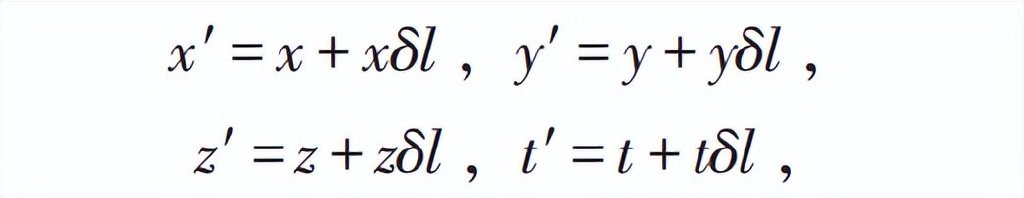對應於李代數中的

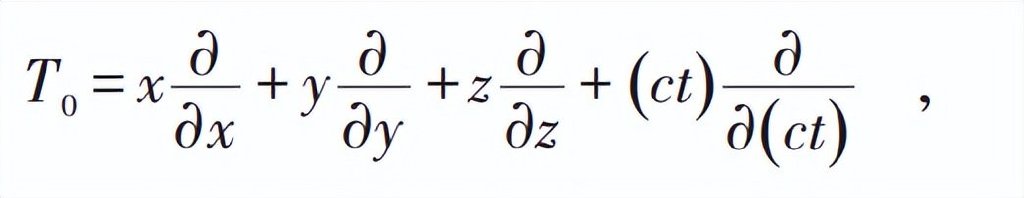
3 洛倫茲羣的發現：演繹的一步

雖然為了突出洛倫茲而不想喧賓奪主，但龐加萊是一個真正的科學家，追求真理永遠是擺在第一位的；對那些實際上已經超越了洛倫茲的新結果，他無法掩着不説出來。定性的，或許可以放在洛倫茲名下講出來，如我們在他的第一個“玩笑”中所見；但定量的，這種做法肯定不行，那就只能不動聲色地低調加以敍述，以下這個只有兩句話的自然段落便是：

“我們也可以用另一種方式產生這個羣。這個羣中的任一變換都可看成是先作一個如下形式的變換，

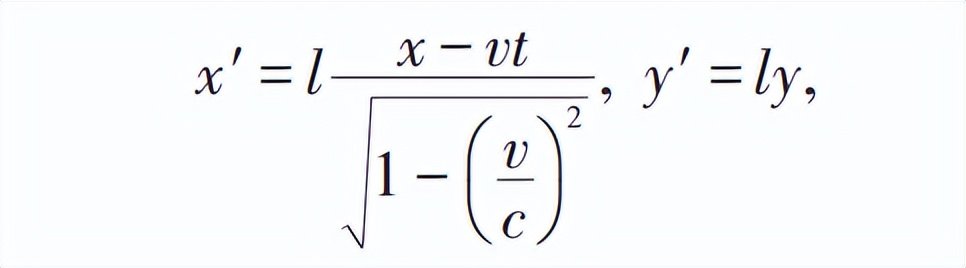
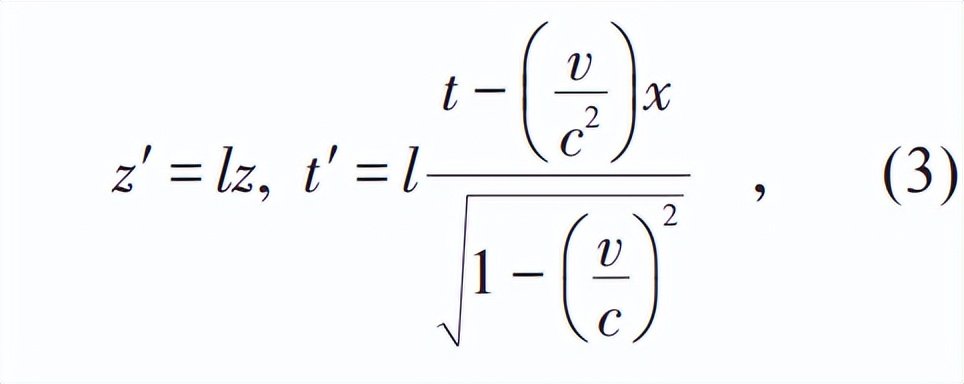接着再作一個合適的空間轉動所構成。”

請注意，如此惜墨如金的龐加萊 (讀者不妨嘗試在原文第4節中去掉任一式子，看看文章是否還成立？)，在這裏不僅完全重複地抄了一遍這一節開頭的第一個公式 (洛倫茲特設公式)，而且還竟然給了這裏的公式(3) (而不是之前的特設公式) 一個編號，這實在太耐人尋味了！常言道，經典值得反覆閲讀；或許我們可以再補充一句，龐加萊的文章更是如此。正是在這裏，龐加萊提示了我們，他所説的“另一種方式”究竟是什麼。同為大數學家的龐加萊，對於大師高斯的名言：“當一幢建築物完成時，應該把腳手架拆除乾淨”一定不陌生，但他在這裏恰恰反其道而行之，“腳手架”幾乎被原封不動地保留了下來，這才使我們比較有把握地復原他所説的“另一種方式”。

的”第二句話，正是用來回答這一問題的；這若無其事的一句話，在C. Moller的相對論名著The Theory of Relativity上，就是整整一節 (§2.4“最一般的洛倫茲變換”) 的內容。龐加萊的這句話事實上是提醒我們，洛倫茲變換式 (最一般的) 與三維空間轉動一同 (而不是僅有前者，否則羣元缺了很多！) 構成了洛倫茲羣，只有基於這樣的理解，所謂物理定律在洛倫茲羣下協變的含義才真正完備。

最後，龐加萊在這一節餘下的部分中，將這個數學上完備的洛倫茲羣運用到真實的物理世界中，即取l=l (v)，然後用羣論的方法簡潔地證明l=1。至此，龐加萊演繹的一步完美收官，整個第4節內容也全部結束。

在對龐加萊一舉奠定狹義相對論數學結構的《七月文章》第4節做了上述詳細介紹之後，當然還應提及一下所有現代大學物理教科書中必不可少的所謂“同時性的相對性”、“時間膨脹”、“長度收縮”這三個幾乎成為相對論“標籤”的問題。事實上，這對於已經建立狹義相對論四維時空幾何圖像的龐加萊而言，可以説完全是小兒科的事了。這裏先直接給出“乾貨”，接着再稍加解釋。龐加萊在《七月文章》的第3節中明白地 (explicitly) 給出了“同時性的相