起源於200年前的彩虹問題，誕生了應用數學的“漸近”世界（下）_風聞

撰文 | Marianne Freiberger

翻譯 | 藏痴

審校 | Dannis

書接上回。正如這篇文章的前半部分講述的那樣，喬治·加布裏埃爾·斯托克斯（George Gabriel Stokes）提出了一種近似艾裏函數的有效方法，這有助於理解彩虹的附屬虹。然而，儘管斯托克斯已經解決了實際問題，但他並不滿意。他對艾裏函數的近似是漸進的，這意味着它只適用於變量x取足夠大正值或足夠小負值的情況。在x=0處這一近似會發散到無窮大。

這本身並不是問題所在，漸進近似對於處理附屬虹的目的來説已經足夠好了。困擾斯托克斯的問題是，他的近似分成了兩部分，分別由截然不同的兩個數學表達式表示。下圖展示了艾裏函數（藍線）和斯托克斯的近似值（紅線），以及近似函數的兩個數學表達式（斯托克斯近似是一個無窮級數，給出的表達式只考慮了級數的第一項）。

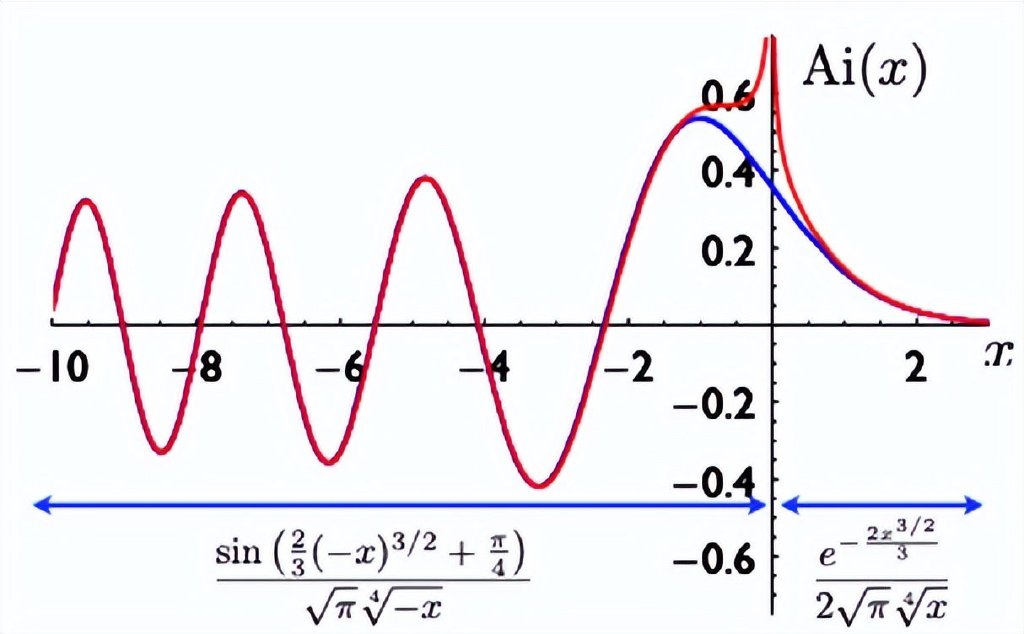藍色曲線是實際的艾裏函數，紅色曲線是斯托克斯的漸進近似。下方公式給出了每一段近似的數學描述。丨圖源：豪斯

如你所見，x>0部分的表達式包含一個指數函數項，而x<0部分包含一個正弦函數。如果瞭解這些函數，你就能發現問題所在。紅色曲線在x=0的右側從無窮大向下迅速衰減到零，這正是負指數函數的性質。而在x=0的左側，紅色曲線按照正弦函數的性質上下振盪。

將正弦寫成指數函數和,令:

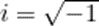那麼正弦函數可以被寫成：

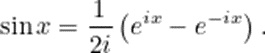現在事實證明，正弦函數可以被表示成兩個指數函數的和。因此，斯托克斯的方案在x>0時有一個指數函數，而在x<0時有兩個，即使原始的艾裏函數並沒有在變量取正值和負值時顯示出這麼明顯的差異。“斯托克斯想要知道的是，如何在變量由負到正時使一個指數函數消失，而在由正到負時產生一個指數函數”，豪斯説。

升高維度

現在很明顯，事情在x=0這一點變得很混亂。這裏是一個奇點，兩部分近似都在這裏發散到無窮大。事實上任何事情都可能在無窮大的地方發生，指數函數可能會消失也可能會產生，所以或許這種現象並不那麼令人驚訝。

然而斯托克斯做了一個當時看來具有革命性的操作。他把自己的近似看成了一個複數變量的函數。如果不知道什麼是複數，你可以把這理解成升高一個維度。所有實數合在一起形成一條線，實變量函數將每個實數（也就是直線上的一個點）映射為另一個實數。複數可以用來代表二維平面上的一個點。復變量函數將一個複數（也就是平面上的點）映射為另一個複數。實數在複數中的表示就是平面內的一條直線，因此複數可以看作實數的擴充，複變函數可以看作實變函數的擴充。（這裏是複數的介紹）

下圖展示了所謂的複平面以及其中的實軸。複變函數將平面上的一個點作為輸入，再給出平面上另一個點作為輸出。我們沒辦法畫出這樣一個函數的圖形，因為這需要四個維度，兩個維度用於輸入，兩個維度用於輸出。

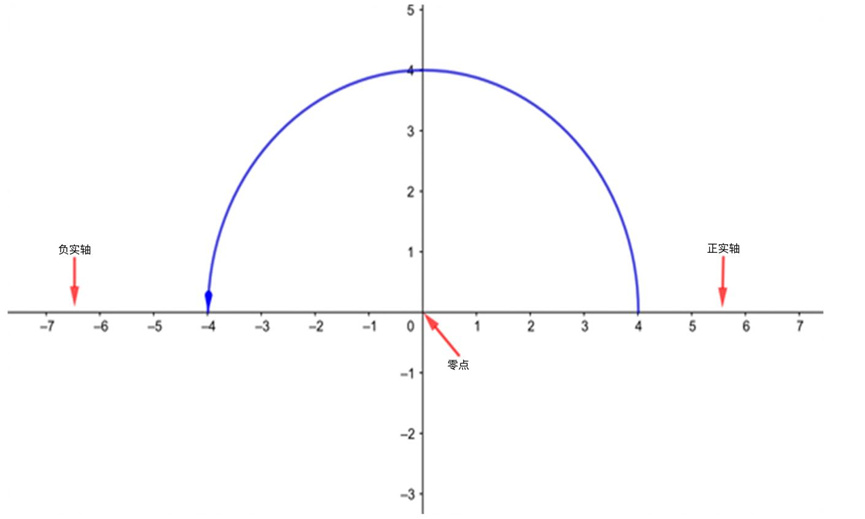複平面及其中水平的實軸。從實軸的正半軸過渡到負半軸並不需要經過零點，而是可以沿着藍色半圓給出的路徑。

一旦開始在複平面上考慮問題，而不僅僅侷限於實軸的話，就有不止一條路徑可以從實軸的正半軸過渡到負半軸。我們可以沿着上圖中的藍色半圓或者其他路徑繞開x=0的點，從而避免奇點的問題。可是，在這個過程中，指數項在哪裏又是如何產生的呢？

躍變的係數

在斯托克斯首次發表艾裏函數近似方法的幾年以後，他發現了這個問題的一部分答案。這裏的數學十分複雜，所以我們只給出梗概。從本質上講，斯托克斯在處理一個關於復變量z的函數的漸進近似，其中包含兩個指數項，每一項都乘以一個係數和一個發散級數。換句話説，他在處理一個看起來像這樣的東西：

如果這兩個係數是收斂的，那麼對於複平面內所有的z，係數A和B可以相等。這意味着，只要A和B都不為0，這個近似就永遠有兩個指數項。但當級數發散的時候，就有更多的可能性。斯托克斯意識到，在這種情況下，係數的數值可以發生躍變。具體而言，一個係數可以在平面的一側等於零，這意味着此處整個漸進近似只包含一個指數項；在平面的另一部分，係數不再等於零，這一區域內漸進近似是兩個指數項的和——這正是艾裏函數的行為。

漸進近似中係數的值發生躍變的行為被稱為斯托克斯現象（ Stokes’ phenomenon）。

（事實上，斯托克斯發現這裏的係數不僅是“可以發生”躍變，而是“必須”躍變。漸進近似必須嚴格滿足的一個條件是，如果從正實軸的z值開始，沿一個完整環路繞零點一圈再回到z，那麼得到的近似值也應該與最開始的值相等。斯托克斯注意到實現這一點的唯一方法是係數發生躍變。這是因為近似表達式中含有復變量的平方根，而這個平方根是多值的——點擊這裏瞭解更多）

斯托克斯線

在確定係數必須在複平面的某個位置發生躍變以後，斯托克斯開始研究這些躍變發生的位置。他發現，如果分開考慮表達式：

中的兩項，考察它們在變量z繞零點環繞一週時的行為，就會發現兩個指數項會輪流取比較大和比較小的絕對值。當一項很大時，另一項就會很小，反之亦然。（這與指數函數的指數的實部是正或負有關。）

係數值的躍變不能影響漸進近似作為一個整體需要滿足的數學——如果係數從零到非零的變化會導致一個指數項的出現，那麼這應該發生在最不顯眼的地方。正因為如此，斯托克斯認為，只能是較小的係數在係數較大項的函數值取最大處發生了躍變。

“斯托克斯説的是，當係數較大的一項處在它函數值最大的位置時，另一項會開始起作用，”豪斯解釋説，“就數值近似而言，如果你想添加一些東西，最好的時機是係數較大的一項處在它最大的位置，而你要添加的東西恰好最小。”

對於艾裏函數，斯托克斯發現，將較小的指數添加進來而對漸進近似函數整體影響最小的位置是在下圖給出的線上，這些線被稱作斯托克斯線，它們與正實軸的夾角按逆時針依次為120°和240°。

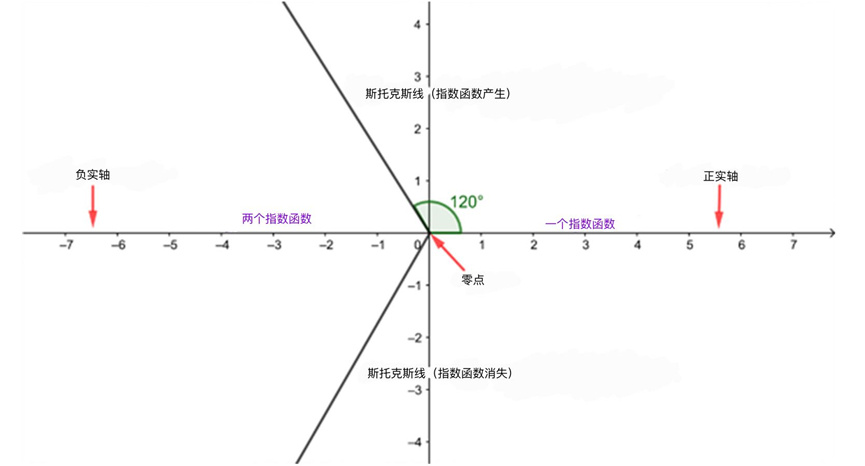從正實軸開始，逆時針繞零點一週。最開始漸進近似只有一個很小的指數函數，這個指數函數一直在增長，直到120°的斯托克斯線處達到最大，此時另一個很小的指數函數被加入並開始增長，到達負實軸時兩個指數項都對整個近似有貢獻。在240°處的第二條斯托克斯線，一個指數函數又被關閉。

“當你從正實軸開始繞零點運動時，在正實軸上衰減的指數函數開始增長，”豪斯解釋説，“到達120°斯托克斯線時，它已經變得很大了，”他説，“如果在斯托克斯線處加入另一個很小的指數，那麼等運動到負實軸時，兩個指數函數大小相當，剛好可以組合成負實軸應有的正弦函數。”

更多問題

正如斯托克斯知曉的那樣，這個以他名字命名的現象不僅發生在艾裏函數上，也發生在其他一整類函數中。這些函數及其漸進近似在應用數學和理論物理中十分常見。當用這種數學處理真實問題的時候，我們並不希望指數項在不被注意的地方出現。“在一個區域它們可能只是指數級小量，但在另一個區域，它們可以再次增長，”豪斯説，“這就是必須考慮它們的原因。”

斯托克斯只是證明了指數項有可能產生，但他並沒有給出指數如何產生的數學證明，這個問題在斯托克斯的解釋一百多年後被再次提出，時至今日科學家仍在研究。

本文經授權轉載自微信公眾號“中科院物理所”，編輯：zhenni，原題目為《斯托克斯眉頭一皺，發現彩虹並不簡單》。

原文鏈接：

https://plus.maths.org/content/stokes-phenomenon-asymptotic-adventure-continued

特 別 提 示

1. 進入『返樸』微信公眾號底部菜單“精品專欄“，可查閲不同主題系列科普文章。

2. 『返樸』提供按月檢索文章功能。關注公眾號，回覆四位數組成的年份+月份，如“1903”，可獲取2019年3月的文章索引，以此類推。