在教科書被改寫之前，我是荒誕的代名詞_風聞

撰文 | Anna Ned

翻譯 | zhenni

審校 | Dannis

來源：https://commons.wikimedia.org/wiki/File:Dan_Shechtman_in_1985.jpg

科學界的八卦一般不會特別流通，但通常你在科學界待的時間越久，就越會容易聽到一些令人驚訝的智力論戰，收穫職業生涯裏一兩個亦敵亦友的夥伴。

其中一段有趣的科學爭論在一位敢於拿職業生涯來打賭的自信工程師和一位二十世紀最偉大的科學家之一——鮑林（Linus Pauling）之間展開。在鮑林於十年後去世的時候——顯然到這一刻他也沒有完全接受這個理論——鮑林的對手收穫到了所有陷入過科學論戰中的人都會夢寐以求的結果。學界在幾年內慢慢接受了他的説法，這位工程師也憑藉他突破性的想法獲得了諾貝爾獎。

晶體學理論

這個故事要從一個理論講起。在進入正題前，我們需要介紹一下人們以往一直用於研究的經驗和工具，由此我們才能理解這個突破有多麼“叛逆”，以至於動搖了人們所熟知的晶體學基礎。

如何將一個或多個幾何形狀鋪滿表面——或者我們稱之為“鑲嵌”問題，是數學領域一個古老而有趣的課題。很長一段時間以來，人們都認為歐幾里得平面不能被一些幾何面（比如正五邊形）平鋪。科學學科中，晶體學限制理論（crystallographic restriction theorem）指出，只有某些週期性方法才能平鋪空間。用材料科學的方式來表述的話，晶體中的原子只能按某幾種週期性進行排列，現代晶體學理論就是以數學中的離散羣論作為基礎的。

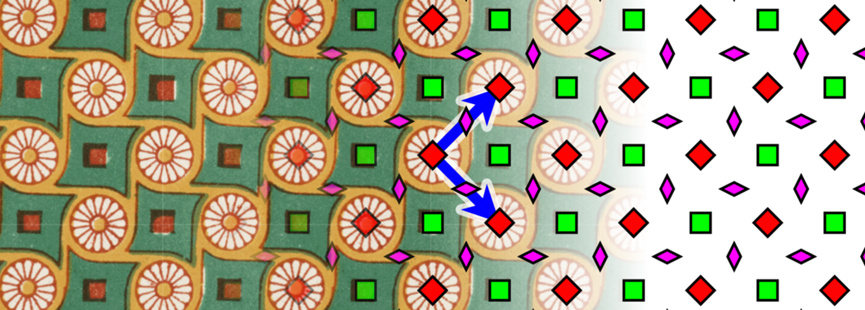來源：https://en.wikipedia.org/wiki/Wallpaper_group#/media/File:SymBlend_p4.svg

晶體學限制定理（原始版本）：

一個晶體的旋轉對稱性（二維或三維空間中）只存在2重、3重、4重和6重旋轉對稱性。

這個定理數學上有更嚴格的證明，但這裏我挑選了一個更簡單、方便理解的：

將相鄰的原子連接成一個正多邊形，其內角和為180°×(n-2)，除以邊數n必須為360°的除數：

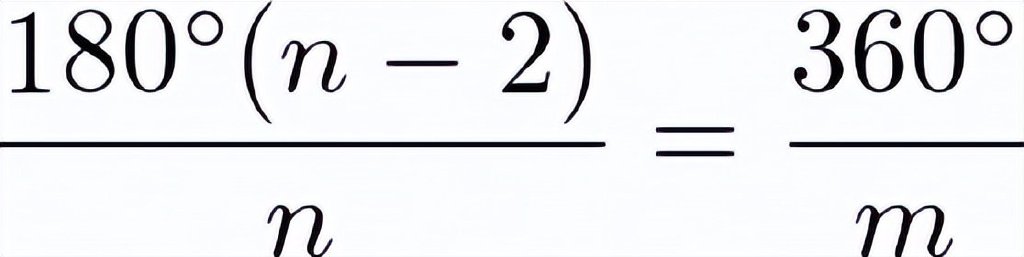那麼：

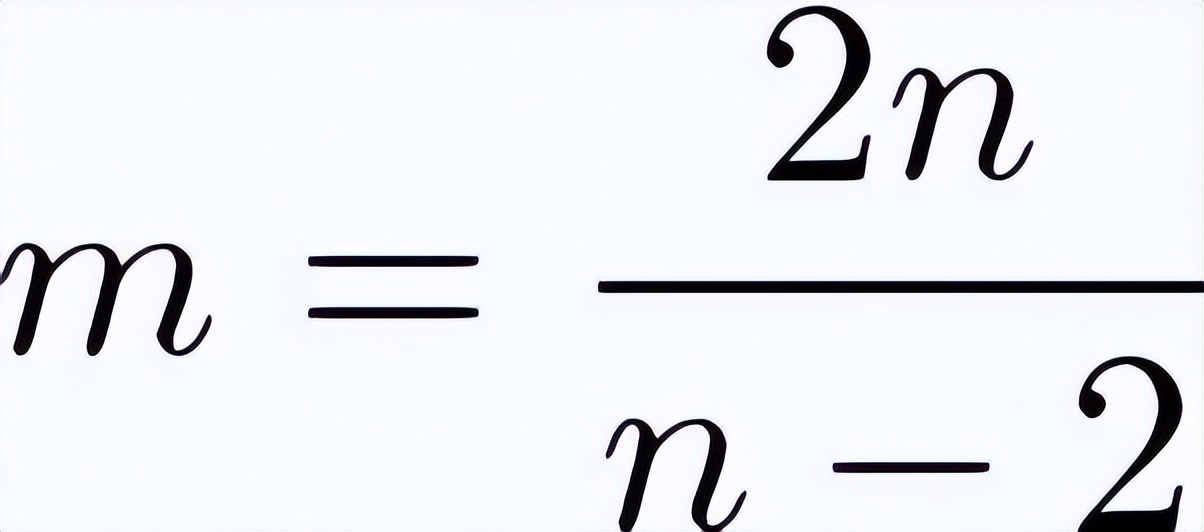m需要為整數，為了滿足等式，則n = 2, 3, 4, 6. 這意味着無限大晶體的對稱性必須滿足2、3、4、6重對稱性。

推 論

從晶體學限制定理可以得出在二維空間中有五種週期性的排列方式，我們稱之為五種晶格，如下圖中所示。這些可以由一組平移操作得到的無限點陣的最小重複單元被稱為布拉菲格子（Bravais lattice）；類似的，三維空間存在14種可能的布拉菲格子，隸屬於七種晶系（三斜、單斜、正交、四方、立方、三方以及六方晶系）。

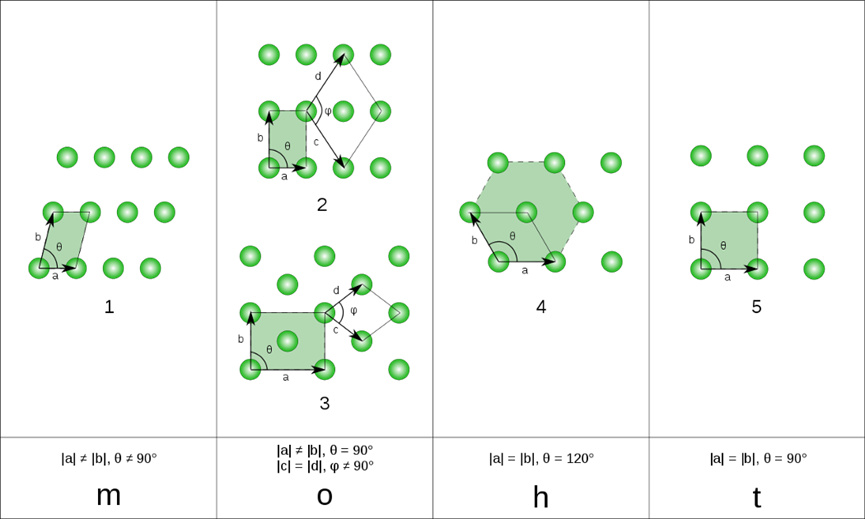二維空間中五種可能的布拉菲格子，屬於四種晶系——單斜（2重旋轉對稱性）、正交（2重旋轉對稱性）、六方（6重旋轉對稱性）和四方（4重旋轉對稱性）晶系。來源：https://upload.wikimedia.org/wikipedia/commons/e/ee/2d-bravais.svg

雖然點羣的數量是無限的（保持固定原點的保距同構），但有了晶體學限制定理約束，只有有限數量的點羣對稱性操作（對映、旋轉、或旋轉對映）能存在於上述晶格中。

週期性宏觀晶體的對稱性可以由以下因素產生：

· 晶格對稱性

· 點羣對稱操作（可以伴隨平移操作——也就是有螺旋軸或者滑移面）

這意味着所有週期性晶體屬於一個有限集合當中的某一種。對於二維平面，所有週期性晶體都有可以按17種二維空間羣（牆紙羣）歸類；而所有三維的週期性結構則歸類進230個空間羣當中。

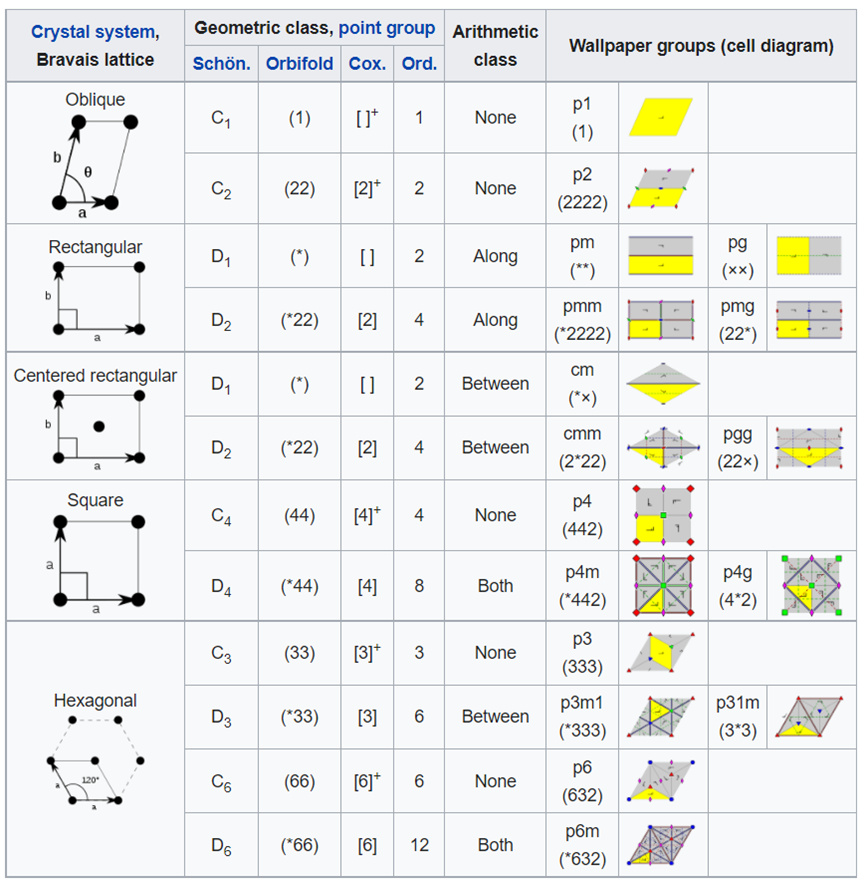17種可能的牆紙羣（wallpaper group）由所有可能的點羣對稱性操作（可以伴隨平移操作）獲得。來源：https://en.wikipedia.org/wiki/Space_group

複雜的現實

但自然界中發現的大多數晶體都是以多晶形式（polycrystalline）存在的，它們由許多單一晶相組成的小區域組成。多晶材料的對稱性通常難以表現出來。

長在木頭上的石巖（岩鹽礦）以多晶的形式結晶，表現出立方對稱性。岩鹽礦（氯化鈉）結構屬於立方晶系，空間羣為Fm-3m。來源：https://commons.wikimedia.org/wiki/File:Halite_on_wood_MNHN_Min%C3%A9ralogie.jpg

純的單晶具有三維230種空間羣中的一種，通常是在實驗室以特定條件生長的（需要特定的温度、壓強、組分濃度等等參數）。幾十年來，專攻晶體生長和晶體學的科學家在晶體制備及探索，還有晶體性質研究等許多方面發展出了大量高精尖技術。

教科書定理之例外

我回顧的這些基本內容在過去的數十年已為人所熟知，這些內容對理解當時晶體學家的觀點和經驗很重要。儘管已經發展出了一系列的相關技術以及用數學語言寫就的晶體學理論，許多有關晶體生長鑑定的挑戰和挫折仍然廣為人知。

熟悉了當時的背景後，當聽到有人聲稱發現了一種具有不可能的五重對稱性的晶體時，你會作何反應呢？

這件事就發生在1984年。在NIST（美國國家標準與技術研究院）研究與收集了兩年的數據後，謝赫特曼（Dan Shechtman）和同事發表了自己的結論，聲稱發現了一種具有二十面體對稱性的晶體，這種晶體具有六個禁止的五重對稱軸。[1]他們觀察到的這種缺乏平移對稱性的晶體並不能按現有的對稱性體系進行分類，儘管這種基於14種三維布拉菲格子的體系在過去的幾十年間已經被廣為認可。

同年，另一個團隊發表了一篇理論分析來支持這一意外的發現。他們提出了一種只有一個旋轉中心的非週期性平鋪方式，並給這種此前未發現的結構起了名字——準晶體（quasicrystal）。[2]準晶體不具有局域的週期性，但是仍能表現出長程有序。

這個發現吸引了一大批關注，但是負面的。

第一個反對的聲音：準晶體之前未在晶體學研究中發現，説明自然界中這樣的結構不能穩定存在。此前科學家們一直都在研究原子可能的排列，但好像是更專注於幾何學的活動，而非對現實材料的研究。

很多人認為一些時候能觀察到的所謂禁止的十重對稱性衍射圖案是孿晶產生的結果，而非真正的被禁止的對稱性。孿晶是兩個分離的晶體共用一個界面相對生長的產物，在晶體學中是一個普通的問題，會造成複雜的衍射圖樣。

屬於四方晶系的金紅石孿晶（二氧化鈦），其空間羣為P42/mnm。來源：https://commons.wikimedia.org/wiki/File:Rutile-41432.jpg

和大人物之間的衝突

萊納斯·鮑林（左）和達尼埃爾·謝赫特曼（右）來源：https://commons.wikimedia.org/wiki/File:Dan_Shechtman_in_1985.jpg

當謝赫特曼首次在所在NIST的研究團隊公佈了自己的數據和結論時，他團隊的領導，同時也是一位在以色列理工學院擔任教授的40歲的科學家説：

“你還是回去好好看看課本吧。”

幾天後，這位領導以“給團隊帶來污點”為由，讓謝赫特曼離開了NIST。從已有的資料我們很難看出，謝赫特曼究竟是在發表數據時被開除的還是被迫休假的。

兩次諾貝爾獎得主（一次化學獎一次和平獎）、在化學和醫藥領域有超過350篇出版物的作者、量子化學創始人之一、被譽為“分子生物學之父”、“化學聖經”的作者 [3]鮑林（Linus Pauling），也是眾多不相信這一發現的人之一。

鮑林立馬私下寫了一封信件，試圖説服作者重新分析這些數據，甚至還申請了一份數據的副本用來自己分析。[4]謝赫特曼立刻回應併發送了數據，還提供了許多支持最初發現的附加數據。即使是這樣一個友好語氣下的辯論，他們倆也沒説服對方。

鮑林告訴謝赫特曼自己會寫一篇對於這個數據的不同解釋。於是在初始發現的一年後，鮑林的不同解釋以論文形式發表在《自然》上——這是一個期刊排名遠高於原始工作發表的期刊。這篇文章也將是關於從謝赫特曼和同事那裏獲得的數據的另外解釋的系列文章的第一篇。

鮑林以這句話給文章結尾 [5]：

“晶體學家們現在可以不用擔心別人質疑自己學科基礎的有效性了。”

一年後，鮑林在與謝赫特曼的深入的私人交流中説，他在自己的數據分析中發現了一個錯誤。鮑林寫道 [4]：

“這個錯誤讓我幾個月的努力打了水漂。”

謝赫特曼説服鮑林這裏並沒有錯誤。意識到自己的問題後，鮑林開始解決這個數據分析的其它“漏洞”，決心解決這個“準晶體問題”。根據已有的信件，兩人的對話在鮑林一方的親切和粗魯之間反覆橫跳。

由於謝赫特曼並不放棄在會議上大方展示自己的發現，鮑林在幾百個科學家面前喊出了下面這段話——他本人也因此而聞名 [6]：

“根本就沒有準晶體這種東西！有的只是‘準科學家’。”

在1987年後，也就是有關於準晶體最開始的論文發表的三年後，二人的對話就沒有記載了。兩人仍然向對方表達了謝意，鮑林這樣寫道：

“你的發現也令我很開心……兩年來我一直致力於這個問題，並在過程中享受許多。我估計已經在上面花費了近1000個小時來思考整個問題，並花費了1000多小時計算和寫論文。”

然而，鮑林好像一直處於堅持解決“準晶體問題”的工作中，許多其他的科學家也在支持和鼓勵他進行這項工作，其中就包括保羅·斯坦哈特（Paul Steinhardt），一開始進行理論計算支持準晶體存在的共同作者之一。在1989的論文中，鮑林抱怨自最初發現的五年來這個課題已經發表了1500餘篇理論和實驗的論文。他寫道 [7]：

“已提出的簡單的準晶體理論需要被修改。”

在最初發現的六年後，鮑林建立了一個包含超過1000個原子的多重孿晶元胞模型來解釋數據 [8]——雖然他又錯了，但值得讚賞的是，在這篇反對的論文於1984年發表時，他已經83歲了。我在1990年後就未在找到他所作的關於準晶問題的文章了，儘管這個問題仍出現在他90歲，也就是1991年的私人筆記裏 [9]。

1992年，國際晶體學聯盟改寫了對晶體的定義。1994年，鮑林去世，享年93歲。

從冒着丟掉工作的風險反叛到獲得諾獎

80歲的謝赫特曼教授如今已經是廣受敬重的科學家了，他在以色列理工學院和愛荷華州立大學任職材料科學教授。儘管他最初的發現頗具爭議，但僅在成果發表三年後，另一個團隊就報告發現了另一種更純、更穩定的準晶體材料 [10]。

從數學的觀點來看，我們也可以理解最初以平移對稱假設為基礎的理論。非週期性的平鋪早在1960年代就被藝術界和數學界所熟知了，最具名氣的非週期性平鋪的例子莫過於二維的彭羅斯平鋪（Penrose tiling）。其三維結構可以類比為二十面體平鋪（icosahedral tiling），和謝赫特曼教授和同事當初觀察的晶系一致。

一些可能的彭羅斯平鋪。來源：https://en.wikipedia.org/wiki/Aperiodic_tiling#/media/File:Penrose_LI_classes.svg

獲得非週期性平鋪的方式有許多，但不像只允許平移對稱性存在的對稱性分類的點羣晶系，可能的非週期性平鋪的數目是無窮多的。

所有三維的週期性晶體都可以被歸類至230種空間羣當中。而準晶可能的數目是無窮的。來源：https://unsplash.com/photos/g95sf8-fEQg

如今謝赫特曼教授已經無懼於分享與鮑林沖突的觀點了，他這樣説道 [11]：

“有很長一段時間我都在反對全世界，我成了一個荒誕的代名詞，是晶體學基礎課程會提到的教材。而與我的發現相對抗的，是以兩度獲得諾獎、美國化學學會的偶像以及世界上最著名的科學家之一的萊納斯·鮑林為首的人們。多年來，直到鮑林臨終前，都在和晶體的準週期性作鬥爭。他錯了，而我在之後的一段時間裏都在享受這個知道他錯了的美妙的科學爭論的過程。”

謝赫特曼的先鋒工作被認可了，他因發現準晶體而獨享了2011年的諾貝爾化學獎。而當我們重看晶體學限制定理，只能嚴謹地將其改成編輯後的版本：

晶體學限制定理（改編版）：

如果平面中一組離散位移具有多個旋轉中心，那麼可能的旋轉只有2、3、4、6重旋轉。

本文經授權轉載自微信公眾號“中科院物理所”，原標題為《成為準諾獎得主的條件竟是讓另一位諾獎得主討厭……？》。

原文鏈接：

NobelPrize to Guy Who Another Laureate Said is Not a Real Scientist | by Anna Ned |Cantor’s Paradise (cantorsparadise.com)

特 別 提 示

1. 進入『返樸』微信公眾號底部菜單“精品專欄“，可查閲不同主題系列科普文章。

2. 『返樸』提供按月檢索文章功能。關注公眾號，回覆四位數組成的年份+月份，如“1903”，可獲取2019年3月的文章索引，以此類推。