電磁感應現象中存在“動生電場”嗎?_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2022-05-26 15:25
 撰文 | 陳昊(普林斯頓大學電氣與計算機工程系 物理系)、沙威(浙江大學信息與電子工程學院)、戴希(香港科技大學物理系)
撰文 | 陳昊(普林斯頓大學電氣與計算機工程系 物理系)、沙威(浙江大學信息與電子工程學院)、戴希(香港科技大學物理系)
來源 | 本文選自《物理》2022年第6期
近期關於電磁學和電動力學的大討論仍在繼續,主要的關注點從之前的運動介質電動力學轉移到了對電磁感應現象的深入剖析。通過討論,筆者發現一些同學甚至是專業的科技工作者對於如感生/動生電動勢、感生 (渦旋) 電場、非靜電力、電勢差等概念存在誤解和混淆。經過初步調研後發現導致這一問題的原因是由於普通高中教育階段可以使用的數學工具有限,新課標高中物理對於電磁感應現象的討論規避了一些技術細節,而一些大學工科中文電磁學教程裏關於這一段的論述又存在錯誤的表述和公式。為了幫助讀者朋友理清相關概念,筆者決定以此內容作為“漫話麥克斯韋方程組”專題的第二篇文章。
1
微觀形式的歐姆定律——電流怎樣流動起來
為簡單起見,我們先探討最簡單的“穩恆電流”,即電路中的電流不隨時間變化的情況。從物理機制上來講,導體中的電流如何流動的規律被總結為“微觀形式的歐姆定律”:導體中的電
 常見的非靜電力有化學電源中的化學作用,發電機中的磁力,濃度不均的體系中的擴散作用,温差電效應等等,它們都可以嚴格或近似地用單位電荷所受到的力來描述,如:
常見的非靜電力有化學電源中的化學作用,發電機中的磁力,濃度不均的體系中的擴散作用,温差電效應等等,它們都可以嚴格或近似地用單位電荷所受到的力來描述,如:
(1) 磁力:f = u×B,其中u是導體在磁場中做切割磁感線運動的速度;
(2) 温差電 (Seebeck效應):f = -S∇T,其中S是Seebeck係數,T是温度。
在這裏,我們要澄清一個比較容易被誤解的點:一些同學學習到電流和電路這一章節的時候,將其與之前所學的靜電場的內容完全割裂開了。通過上述的歐姆定律,我們清晰地看到:在電路中驅動電荷做定向流動的是靜電場E與單位電荷所受的非靜電力f這兩者;而在一般的電路中,非靜電力僅在電源內部(內電路)存在。因此在整個外電路中,驅動電荷運動的只是靜電場本身。這個靜電場是哪裏來的呢?答案其實非常有意思,它與我們在初中第一次學習電路時就知道的一個事實“穩恆電路中同一根導線中的電流處處相等”息息相關。設
 荷守恆,會有正電荷在圖中拐角處積累。這樣一來,累積起來的正電荷就會產生一個方向向外的電場,累積的越多則電場越強。從圖中可以看出,這個電場在流入電路的部分與電流方向相反,減小了單位電荷所受的合力,而在流出電流的部分與電流方向相同,增大了單位電荷所受的合力。根據上述的歐姆定律,我們立即知道隨着電荷的累積,流入的電流會逐步減小而流出的電流會逐步變大,直到二者相等,則電荷不再累積,電流也不再變化,電路達到穩定狀態。在實際的電路中,靜電場幾乎無處不在,其來自於在電路中積累的電荷,反饋式地調節着電路中各個部分的電流大小。
荷守恆,會有正電荷在圖中拐角處積累。這樣一來,累積起來的正電荷就會產生一個方向向外的電場,累積的越多則電場越強。從圖中可以看出,這個電場在流入電路的部分與電流方向相反,減小了單位電荷所受的合力,而在流出電流的部分與電流方向相同,增大了單位電荷所受的合力。根據上述的歐姆定律,我們立即知道隨着電荷的累積,流入的電流會逐步減小而流出的電流會逐步變大,直到二者相等,則電荷不再累積,電流也不再變化,電路達到穩定狀態。在實際的電路中,靜電場幾乎無處不在,其來自於在電路中積累的電荷,反饋式地調節着電路中各個部分的電流大小。
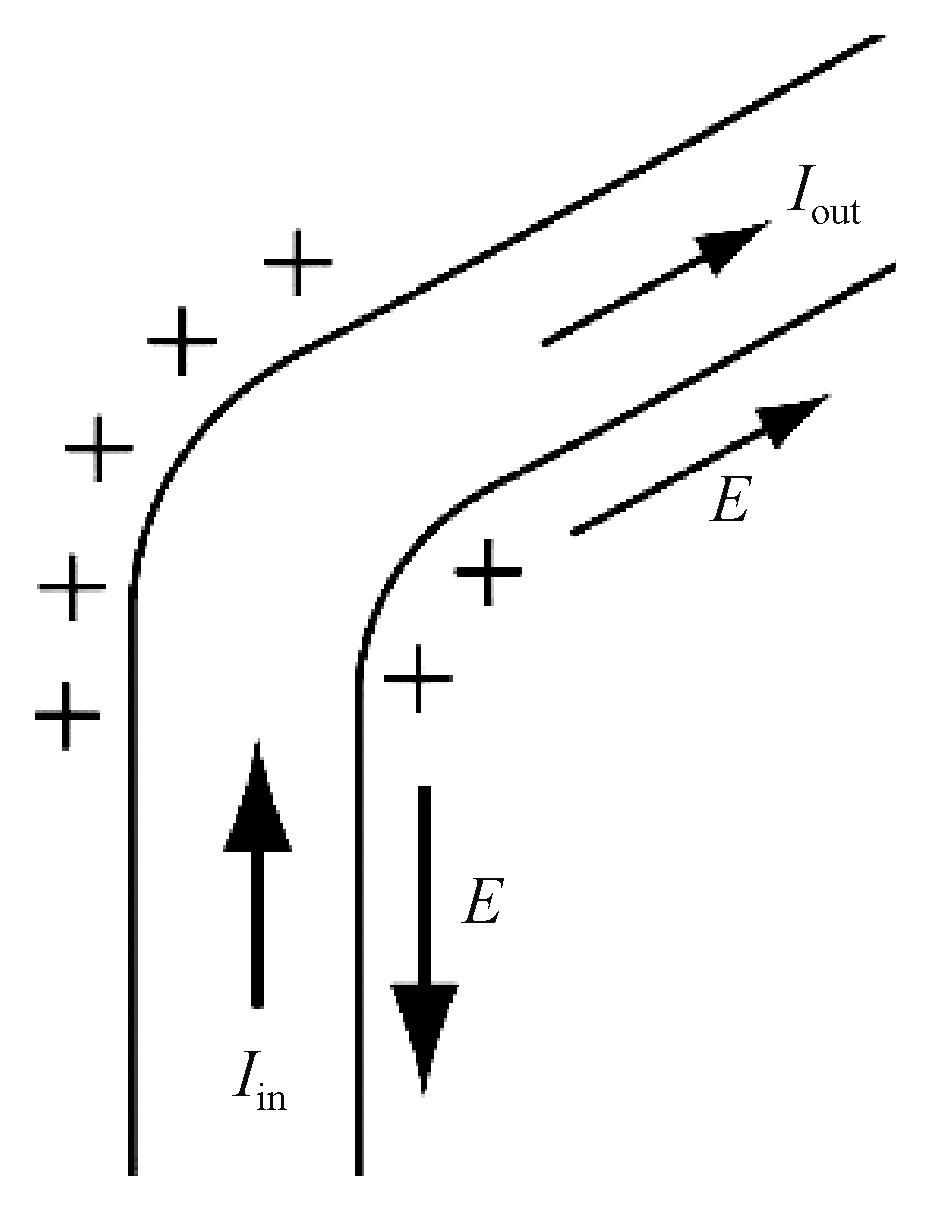 圖1 一段電路(下文的論證與電路的形狀無關,畫出一個“拐角”只是為了可以指代清楚)(圖片來源:格里菲斯《電動力學導論》)
圖1 一段電路(下文的論證與電路的形狀無關,畫出一個“拐角”只是為了可以指代清楚)(圖片來源:格里菲斯《電動力學導論》)
細心的讀者可能注意到前文提到了“穩恆電路”的條件,事實上,即使是在交變電流的情況下,只要電路中的電流變化不是很快 (交流電路的(角)頻率ω足夠低:ω<<c/L,其中c是光速,L是電路的長度尺度) ,則在電流發生改變時,電荷重新分佈的速度都遠比它快得多。因此在任意時刻,交變電路都可以看成是一個“瞬時的穩恆電路”,上面的所有論述仍然是成立的 (電流密度的散度處處為0) 。這其實也是“電路”這一模型的適用極限:如果頻率過高,則不能再用電路中諸如“電壓”、“電阻”、“電容”等概念進行分析,而要使用完整的電磁場理論,將電路看成電磁介質,仔細討論電荷和電磁場的動力學問題,這樣的“電路”就成為波導了。我們可以把這種電流變化足夠緩慢的情況稱之為“近穩恆電路”,它實際上就是筆者在“漫話麥克斯韋方程組”專題的第一篇文章中提到的“準靜態近似”的情況(例如電容器是“電學準靜態近似”,電感器是“磁學準靜態近似”,而電阻器既可以看作是電學也可以看作是磁學準靜態近似),在此不再贅述,有興趣的讀者可以參考2022年三月刊的《物理》雜誌[1]或“中國物理學會期刊網”微信公眾號。不過需要強調的一點是:在電流可以隨時間改變的一般情形下,本節中提到的由電荷積累產生的“靜電場”應改稱之為“縱向電場”,其對電荷產生的作用力就是“靜電力”。
2
電動勢與電勢差——從微觀到宏觀
在上一節,我們通過微觀形式的歐姆定律明白了電荷在電路中穩定流動形成電流的物理原因——非靜電力和縱向電場產生的靜電力。不過這一規律在實際問題中非常難以應用,因為電路中的縱向電場是電路中的電荷自行分佈達到平衡從而形成的,既不受我們的控制,也無法簡單地測量出來。為了得到更有實用價值的物理規律,物理學家將上述表達式乘上


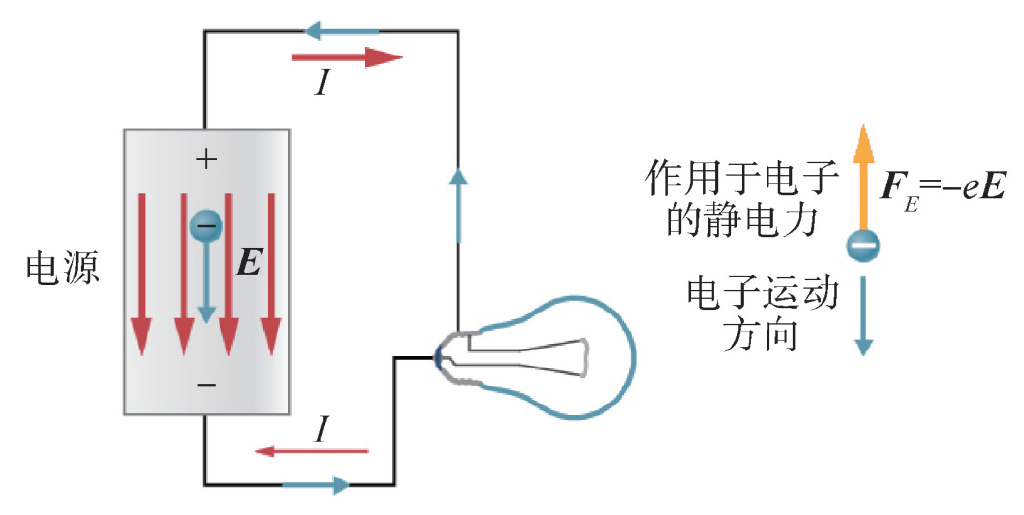 圖2 放大了電源結構的電路模式圖
圖2 放大了電源結構的電路模式圖
近期,筆者通過一些機會與學校裏的本科生交流後發現他們中有不少人混淆了電動勢與電勢差的概念。經過深入仔細的思考和討論,筆者認為問題的根源是“電源開路電壓與其電動勢相等”這一事實。由於沒有對這一事實的微觀機制的充分認識,導致不少同學認為電源的開路電壓“就是”電源的電動勢。其實,只要對我們本節和上一節中提到的內容有了正確的理解,就不難對這兩個概念進行辨析。圖2是一個模式化的電路,電路的左側是電源,在外電路沒有接入時,其內部產生非靜電力將正電荷向其上端的正極移動 (同時將負電荷向其下端的負極移動),從而在電源正極積累一些正電荷,在負極積累一些負電荷。這種不均衡的正負電荷分佈會產生一個由正極指向負極的電場,對正電荷產生向負極方向的靜電力,對負電荷產生向正極方向的靜電力,阻礙非靜電力導致的流動。隨着電荷的累積越來越多,縱向電場也越來越強,直到縱向電場力 (靜電力) 與非靜電力在電源內部處處平衡:E+f=0,則電荷不再流動並積累,體系達到穩定狀態。這時,正極積累的正電荷和負極累積的負電荷構成的電場使得正負極之間產生了電勢差V+-,其滿足:
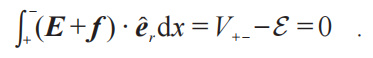 注意計算電源電動勢時應該沿着單位正電荷受到的非靜電力的方向從負極到正極積分 (即非靜電力將正電荷從負極帶到正極克服靜電力所做的正功),所以E前面出現的負號是由於我們的積分方向是從正極到負極。由此可見開路情況下正負極之間的電勢差正好等於電源的電動勢。
注意計算電源電動勢時應該沿着單位正電荷受到的非靜電力的方向從負極到正極積分 (即非靜電力將正電荷從負極帶到正極克服靜電力所做的正功),所以E前面出現的負號是由於我們的積分方向是從正極到負極。由此可見開路情況下正負極之間的電勢差正好等於電源的電動勢。
3
導體切割磁感線運動產生的電動勢——動生電動勢
為了展示電動勢的具體計算,也為了稍後展開有關電磁感應現象的討論,下面針對一個簡單的例子計算並討論導體切割磁感線的過程中產生的電動勢。假設在強度為B的勻強磁場中,一根長度為L的導體棒放置在垂直於磁場的平面內。我們知道,如果此時令導體棒沿着垂直於自身和磁場的方向以速度u運動,則由於其做切割磁感線運動,磁場會對導體棒內部的電荷產生磁力作用。由於磁力也是一種非靜電力,則導體棒成為了一個電源,有了電動勢。如何計算這個電動勢的大小呢?根據電動勢的定義:
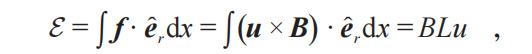 這種導體切割磁感線時由磁力導致的電動勢被稱為“動生電動勢”。這裏要注意一點,跟我們接下來要介紹的“感生電動勢”不同,“動生電動勢”絕不對應什麼“動生電場”的概念,更不是什麼“動生電場”沿着電路的積分了。
這種導體切割磁感線時由磁力導致的電動勢被稱為“動生電動勢”。這裏要注意一點,跟我們接下來要介紹的“感生電動勢”不同,“動生電動勢”絕不對應什麼“動生電場”的概念,更不是什麼“動生電場”沿着電路的積分了。
 靜電力沿着電路方向的分量,而不是整個非靜電力。其次,這個積分是一個“等時積分”,意思是我們並不關注導體棒內的電荷實際上是怎麼在非靜電力的作用下從導體棒一端經過一段時間運動到另一端的,而是在我們所要研究的時刻給系統拍一張快照,在照片拍攝的這一時刻,計算一單位電荷在導體棒內各個位置所受的非靜電力f(x),以此作為定義式中的f進行積分,得到電動勢。經過這一辨析,筆者發現將電動勢描述為“非靜電力對單位電荷做的功”實際上容易產生歧義,因為在電路中有隨時間變化的部分時電動勢並不是非靜電力對任何實際運動的電荷所做的功。為消除這一歧義,最好將電動勢描述為“非靜電力沿電路分量的等時線積分”。(讀過“漫話麥克斯韋方程組”第一篇文章[1]的讀者可能已經敏鋭地察覺到,由於相對論效應,這裏可能存在“等時”在不同參考系下不一致的問題,請不要着急,筆者會在本文倒數第二節通過一個簡單的示例展示電磁學理論與相對論在這裏是如何相符的。)
靜電力沿着電路方向的分量,而不是整個非靜電力。其次,這個積分是一個“等時積分”,意思是我們並不關注導體棒內的電荷實際上是怎麼在非靜電力的作用下從導體棒一端經過一段時間運動到另一端的,而是在我們所要研究的時刻給系統拍一張快照,在照片拍攝的這一時刻,計算一單位電荷在導體棒內各個位置所受的非靜電力f(x),以此作為定義式中的f進行積分,得到電動勢。經過這一辨析,筆者發現將電動勢描述為“非靜電力對單位電荷做的功”實際上容易產生歧義,因為在電路中有隨時間變化的部分時電動勢並不是非靜電力對任何實際運動的電荷所做的功。為消除這一歧義,最好將電動勢描述為“非靜電力沿電路分量的等時線積分”。(讀過“漫話麥克斯韋方程組”第一篇文章[1]的讀者可能已經敏鋭地察覺到,由於相對論效應,這裏可能存在“等時”在不同參考系下不一致的問題,請不要着急,筆者會在本文倒數第二節通過一個簡單的示例展示電磁學理論與相對論在這裏是如何相符的。)
再進一步,如果我們給這個“導體棒電源”接上一個外電路,則電流會沿着單位正電荷所受非靜電力的方向從導體棒的一端流向另一端。此時,在實驗室參考系看來:電荷並不是沿着導體棒的方向運動的,而是與之有一個夾角,可以分解成沿導體棒和垂直於導體棒兩個方向的運動。由於磁力本身不做功,功率為0(磁力點乘合速度=0),經過簡單計算不難發現,磁力沿導體棒的分量對電荷做功功率為正,而磁力垂直於導體棒的分量對電荷做功功率為負,兩者絕對值相等,正好相抵。如果我們就這樣放任不管,則磁力垂直於導體棒的分量 (實際上就是導體棒受到的安培力) 將阻礙導體棒繼續勻速運動。為保持其勻速運動,需要對導體棒施加等大反向的額外的力去平衡安培力,這一外力做功功率為正,也與安培力做功的功率絕對值相等。這樣一來,我們發現磁力在其中起到了類似機械中“滑輪”的作用,將我們施加在導體棒上的力轉了90°角,將能量“傳遞”給了電荷。
4
變化的磁場產生感生電場——一種非靜電力
前一節中我們介紹了動生電動勢。學過電磁學的同學們都知道,動生電動勢有個好兄弟,叫“感生電動勢”,甚至有一些同學經常把它們混為一談。下面我們還是從電磁場和微觀的物理機制入手,講解感生電動勢的來源。
 這種由變化磁場產生的電場是一種渦旋電場,它無源有旋,作用在電荷上的力的規律與靜止的電荷產生的縱向電場一致。從命名上就能看出,這種力也是一種非靜電力,由其導致的電動勢稱為“感生電動勢” (為避免歧義,我們此處的命名遵循教育部制訂的普通高中新課程標準。另一個相近的名詞“感應電動勢”有其他的含義,詳見下節) 。在電磁學的理論中,科學家們一般不將這種感生電場與縱向電場分開,而是統一稱為電場。但在電路理論中,由於靜電力與非靜電力承擔着完全不同的角色,我們還是傾向於把這種感生電場與縱向電場清晰地區分開來,簡單地看成一種非靜電力就好了。能夠這樣做拆分的原因實際上也是因為在準靜態近似下,縱向電場的動力學是可以從其餘的電磁場中解耦的[2]。
這種由變化磁場產生的電場是一種渦旋電場,它無源有旋,作用在電荷上的力的規律與靜止的電荷產生的縱向電場一致。從命名上就能看出,這種力也是一種非靜電力,由其導致的電動勢稱為“感生電動勢” (為避免歧義,我們此處的命名遵循教育部制訂的普通高中新課程標準。另一個相近的名詞“感應電動勢”有其他的含義,詳見下節) 。在電磁學的理論中,科學家們一般不將這種感生電場與縱向電場分開,而是統一稱為電場。但在電路理論中,由於靜電力與非靜電力承擔着完全不同的角色,我們還是傾向於把這種感生電場與縱向電場清晰地區分開來,簡單地看成一種非靜電力就好了。能夠這樣做拆分的原因實際上也是因為在準靜態近似下,縱向電場的動力學是可以從其餘的電磁場中解耦的[2]。
在結束本節之前,我們還要再次強調:雖然在歷史上,動生和感生電動勢都被稱作是“法拉第電磁感應定律”的一部分,但它們是由完全不同的物理機制產生的。導致動生電動勢的非靜電力就是我們所熟悉的磁力 (洛倫茲力),動生電動勢並不對應什麼“動生電場”;而產生感生電動勢的非靜電力則是一種全新的物理現象:由變化的磁場感應出的渦旋電場 (感生電場)。它們之間不可以做簡單的類比,更不可以混淆。在接下來的幾節裏,我們將探討動生和感生電動勢之間的聯繫,但不論它們之間的聯繫有多麼緊密,它們都是完全不同的兩種物理現象。
5
法拉第電磁感應定律(通量定理)——將動生電動勢與感生電動勢
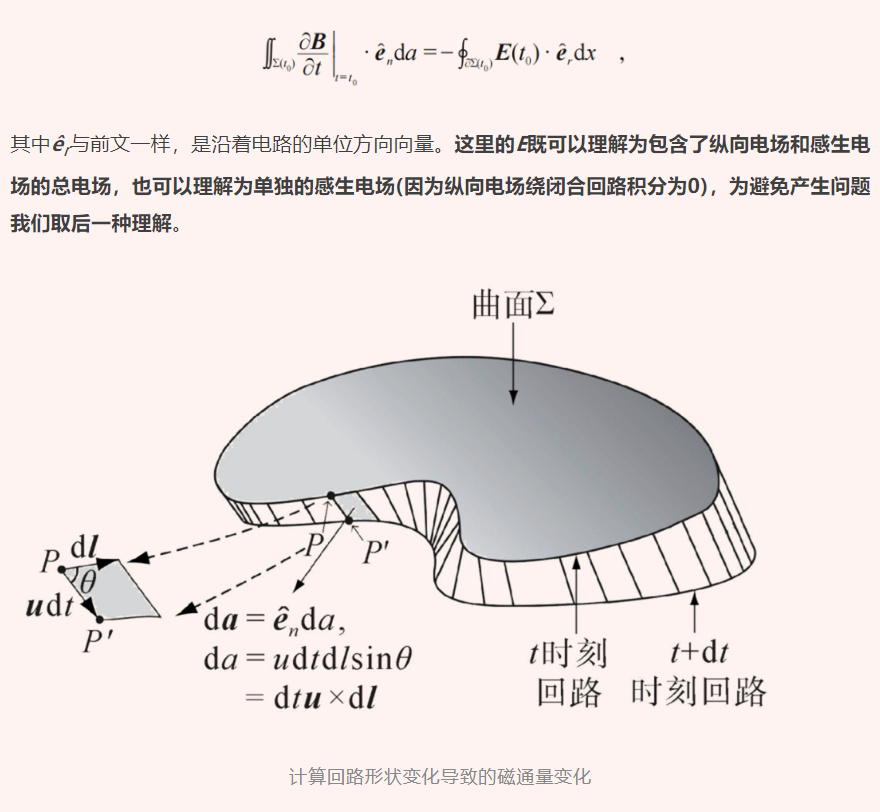
人教版新課標高中物理教材對於法拉第電磁感應定律的表述為:閉合電路中感應電動勢的大小,與穿過這一電路的磁通量的變化率成正比 (只表示感應電動勢大小,其方向可以使用楞次定律判斷) 。這一定律 (也稱“通量法則”) 深受一些同學的喜愛,因為這裏的“感應電動勢”包括了前文提到的動生電動勢和感生電動勢兩者之和,在做具體計算時就可以不去細究電動勢的產生機制了。而經過前文的討論,我們已經認識到動生和感生電動勢完全是兩種不同的物理現象,那麼從某種意義上來講,這一混合了兩種物理現象的“電磁感應定律”從理論的角度來説是一種用於方便計算的二級結論,是將麥克斯韋方程應用於大多數電路體系的推論。在附錄2中,我們從前文介紹的基本原理和物理機制出發,對通量法則進行了證明 (需要多變量微積分的知識)。從證明中可以看到:雖然通量法則從形式上統一了動生和感生兩種電動勢,但如果想得到通量法則,必須要求電路是由很細的導線組成的閉合迴路,從而用數學上的閉合曲線進行描述,而這只是實際電路中比較特殊的情況。早在上世紀60到80年代,國內外就有不少教育家針對電路的迴路無法清晰定義的情況進行了討論。著名物理學家理查德·費曼在其《物理學講義》中以非常清晰的方式闡述了通量法則的兩個反例 (圖3),有興趣的同學可以去閲讀第二卷17-2節 (https://www.feynmanlectures.caltech.edu/II_17.html)。筆者還在1985年前後的《大學物理》雜誌中看到了十餘篇有關通量法則的論文,各路學者從不同的角度深入剖析通量法則的適用性和例外情況,令人醍醐灌頂,其中以1987年07期的北京大學趙凱華教授的《通量法則反例問題》最為精湛。這些論文現在都可以在《大學物理》網站 (http://dxwl.bnu.edu.cn) 檢索到。有條件的讀者不妨去下載下來讀一讀,一定會有所裨益。
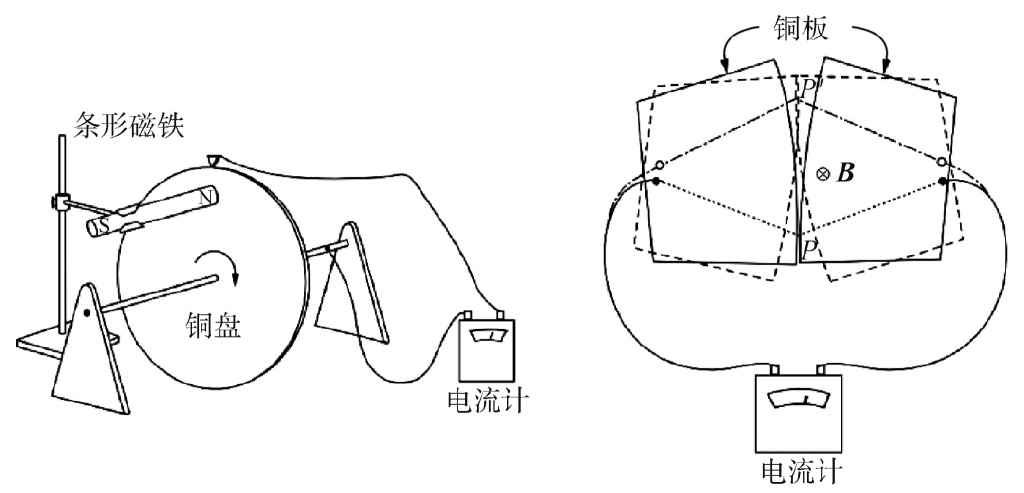 圖3 《費曼物理學講義》中提到的兩個“通量定理”的反例
圖3 《費曼物理學講義》中提到的兩個“通量定理”的反例
綜上所述,通量定理是揉合了動生與感生兩種不同的電動勢的一個二級結論。雖然使用通量定理可以方便計算,但我們仍然要對兩種電動勢的產生機制有清晰透徹的定性與定量理解。
6
不同參考系下看電磁感應
講到這裏,尤其是對於讀過“漫話麥克斯韋方程組”專題第一篇文章的讀者來説,在不同的參考系中考察感生和動生電動勢已經是不可避之的了。下面我們就通過一個簡單且常見的例子,介紹如何在不同的參考系中討論感應電動勢的問題。

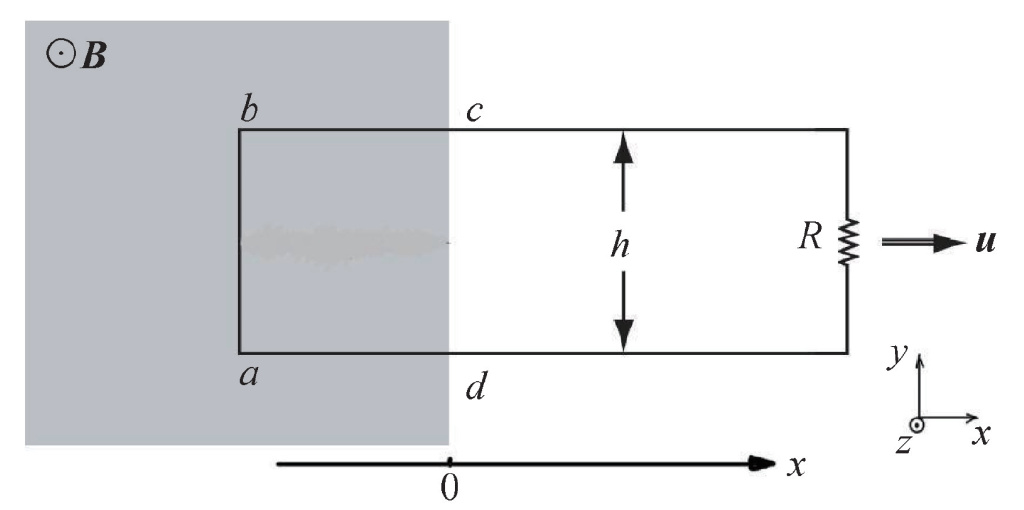 圖4 實驗室參考系下,線框正以速度u離開磁場區域 (陰影區為勻強磁場)
圖4 實驗室參考系下,線框正以速度u離開磁場區域 (陰影區為勻強磁場)
下面我們換到線框靜止的參考系 (隨動系) 中考察該問題。在隨動系下,線框靜止,沒有動生電動勢;磁場雖然大小和方向不隨時間改變,但其存在的區域卻在發生改變,因此這是一個隨時間變化的磁場,會產生感生電動勢。為了求解感生電動勢的大小,我們首先要求解隨動系下的電磁場。根據時空座標和電磁場的參考系變換公式 (公式中帶撇的隨動系相對不帶撇的實驗室系的速度為u):
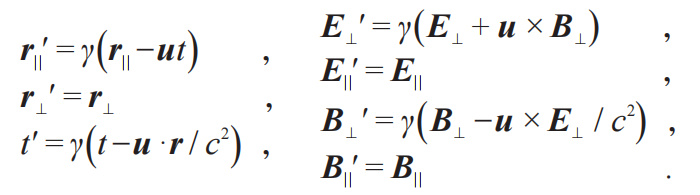
 有興趣的讀者可以嘗試使用通量定理分別計算兩個參考系中的電動勢 (在計算隨動系中的磁通量時請注意:隨動系下磁感應強度與實驗室系不同,可由上文提到的電磁場參考系變換公式得到),將得到與以上相同的結果。
有興趣的讀者可以嘗試使用通量定理分別計算兩個參考系中的電動勢 (在計算隨動系中的磁通量時請注意:隨動系下磁感應強度與實驗室系不同,可由上文提到的電磁場參考系變換公式得到),將得到與以上相同的結果。
由此我們發現:不同參考系下的電動勢是不一樣的。這是由於電動勢的定義是一個“等時”積分,而在相對論的閔可夫斯基時空中,不同參考系中的“同時性”不是絕對的,因此電動勢不構成一個在洛倫茲變換下不變的 (四維協變) 標量。通過這個簡單的例子,我們更加深入地理解了電動勢的定義是依賴於參考系的,並且動生電動勢與感生電動勢緊密結合在一起:對於同一物理過程,產生的是動生還是感生電動勢以及電動勢的大小都與參考系的選取有關。(在低速近似下,γ≈1,電動勢在兩參考系下近似相等。)
同時,我們發現一些長期從事教學工作的同事意識裏的“動生電場”其實就是從參照系變化來的,他們認為實驗室參照系裏的動生電動勢是由洛倫茲力中v×B這一項貢獻的,而這一項也“恰好”是隨動參照系中電場E ′的低速近似 (即把洛倫茲變換中的γ因子近似為1),因此稱之為“動生電場”。我們認為這種説法是很不嚴謹的,因為在隨動參照系裏線圈是不動的;根據上面的討論,在隨動參照系裏測到的電動勢恰恰是感生電場引起的。通過洛倫茲變換改變參照系的時候,電場和磁場是要互相轉換的,所以我們在討論問題的時候必須首先搞清楚參照系,同一參照系下的物理量才可以放在一起考慮。“動生電場”的錯誤叫法是典型的混淆不同參照系下物理量的錯誤。它導致一種似乎麥克斯韋方程組裏沒有包括“動生電場”,似乎是不完備的錯覺。更值得一提的是,《電磁場與電磁波》本科教材的修訂版[第四版],將原版[第二版]正確的隨動參照系電場的迴路積分,錯寫成了實驗室參照系電場的迴路積分,得到了錯誤的法拉第定律的微分形式。事實上,麥克斯韋方程組裏沒有“動生電場”,因為它本來就不存在,導致動生電動勢的是運動導體中的電荷在磁場下受到的洛倫茲力。
6
電磁動力學定律的完備性——場方程與洛倫茲力方程
在這篇文章的最後,筆者想要額外解釋一下電磁學定律的完備性的問題。我們經常能聽到一種觀點:麥克斯韋用四個方程組統一了複雜的電磁現象,豐富的電磁現象完全包含在這簡潔的四行方程中。拋開歷史過程不談,這一論述中的科學內容並不嚴謹。麥克斯韋方程組確實將大量的電磁現象總結在了一起,甚至可以從中推導出電荷守恆定律;但要想完整地描述電磁學,僅靠麥克斯韋方程組是不夠的。麥克斯韋方程組是電磁場的動力學方程和約束條件,它僅描述了電荷 (電流) 與電磁場以及電磁場之間的局域關係。在麥克斯韋方程組中,電荷和電流是作為外部參量存在的。完備的電磁學理論一定還需要將電荷的動力學規律納入進來——如果攜帶電荷的物質可以用經典力學來描述,對應的動力學規律就是洛倫茲力方程F=q(E+v×B)與牛頓第二定律,如果是量子體系則是以矢勢A耦合到相應的薛定諤方程。在有電磁介質存在的情況下,我們通常使用麥克斯韋方程組和介質的本構關係來解決電磁學問題。實際上,介質的本構關係描述的是介質中的電荷和分子電流對於電磁場的響應,從根本上來講是由上述攜帶電荷的物質場的動力學規律導出的。這一根本邏輯即使是到了用量子理論描述物質的今天也沒有改變。麥克斯韋方程組加上物質的動力學規律 (對於經典系統即洛倫茲力定律) 就是完備的電磁動力學定律 (如果這個世界上只有電磁這一種相互作用,則聯立麥克斯韋方程組和描述物質的動力學方程即從原則上可求解一切物理問題)。在沒有新的實驗現象發現之前,這就是電動力學物理規律的“最終版本”。本文作者之一戴希教授前段時間也在知乎上表示:“任何其他版本的電磁學方程或者理論要麼跟麥克斯韋方程加洛倫茲力定律在數學上嚴格等價,要麼就是錯的,沒有第三種可能性。”除非有新的實驗現象 (例如磁單極子) 被觀察到,否則試圖隨意修改麥克斯韋場方程的一切嘗試 (嚴格的數學恆等變換除外) 都將走向謬誤。
附錄


 謹以此文向上世紀後半葉對相關問題進行深入細緻討論,併為傳遞準確的科學知識而辛勤工作的中外老一輩教育工作者致以崇高的敬意。
謹以此文向上世紀後半葉對相關問題進行深入細緻討論,併為傳遞準確的科學知識而辛勤工作的中外老一輩教育工作者致以崇高的敬意。
參考文獻
[1] 戴希,沙威,陳昊. 物理,2022,51(3):145
[2] Chen H,Sha W E I,Dai X et al. Progress In ElectromagneticsResearch,2022,174:1
[3] 格里菲斯 大衞·J 著,賈瑜 註釋. 電動力學導論(英文註釋版·原書第4版). 北京:機械工業出版社,2021
[4] 傑克遜 J D 著. 經典電動力學(第3版影印版). 北京:高等教育出版社,2004
[5] 愛因斯坦 著,楊潤殷 譯,胡剛復 校. 狹義與廣義相對論淺説.北京:北京大學出版社,2018
[6] 泡利 W 著,洪銘熙,苑之方 譯,留潤州 校. 泡利物理學講義(第 一、二、三卷). 北京:高等教育出版社,2014
[7] 趙凱華,陳熙謀. 新概念物理學教程:電磁學. 北京:高等教育出版社,2003
[8] 普通高中教科書:物理(必修 第三冊). 人民教育出版社
[9] 普通高中教科書:物理(選擇性必修 第二冊). 人民教育出版社
[10] 電磁場與電磁波(第二版)(原始版). 高等教育出版社,1987
[11] 電磁場與電磁波(第四版)(修訂版). 高等教育出版社,2006
本文經授權轉載自微信公眾號“中國物理學會期刊網”。
特 別 提 示
1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閲不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回覆四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。