數學證明到底是什麼?丨展卷_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2022-06-19 11:34
數學史家,穆倫堡學院名譽Truman Koehler數學教授威廉·鄧納姆在1994年出版The Mathematical Universe一書,用26個英文字母作為標題講述數學史上重要的問題和人物。本文選自J——Justification,論證。數學與其他學科最大的不同就在於,命題需要證明。數千年來數學正因為此發展進步,人類一步步攀上智慧的高峯。而且,在作者看來,“數學證明的標準不同於其他任何人類活動領域中的標準。“那麼,數學定理的證明到底是什麼呢?本文給出了四個基本原則,闡述涉及數學證明本質的非常有意義的問題。

本文經授權選自《數學那些事:偉大的問題與非凡的人》(圖靈|人民郵電出版,2022.3),標題為編者所加。前往“返樸”公眾號,點擊文末“閲讀原文”可購買此書。點擊“在看”並發表您的感想至留言區,截至6月26日12:00我們會選出2條留言,每人贈書一本。
今日微博福利,關注@返樸 ,轉發本微博並@ 一名好友,截至6月26日12:00我們會選出1位粉絲,贈《數學那些事:偉大的問題與非凡的人》(圖靈|人民郵電出版,2022.3)一本。
撰文丨威廉·鄧納姆(William Dunham,美國穆倫堡學院數學教授)
翻譯丨馮速
“證明,”數學家邁克爾·阿蒂亞(Michael Atiyah,1929-2019)曾説,“它是膠水,把數學粘到了一起。”顯然,這一觀點想説的是,證明或者説論證是數學的化身。
這樣的觀點可能會引起爭議。數學這個學科涉及的範圍如此廣泛,它可以包含各種活動,如估值、構造反例、測試特殊案例以及解決日常問題等。數學家也不必每天24小時都在證明定理。
然而,即便理論命題的邏輯論證不是數學的全部活動,它也肯定是這個學科的特徵。數學離不開其他各個方面的學術努力,就像它離不開證明、推理以及邏輯演繹一樣。在比較數學與邏輯的關係時,伯特蘭·羅素斷言:“已經無法在二者之間劃出界線了;事實上,二者是一體的。”
本書已經分析了很多數學論證。在第 A 章(Arithmetic 算術)中,我們證明了質數的無窮性;在第 H 章中,我們證明了畢達哥拉斯定理。就一般數學論證而言,這些證明相當簡單。其他論證卻需要很多頁、很多章節,甚至很多卷才能得出它們的最終結論。相應的智力要求不見得適合每一個人,正如謙遜的查爾斯·達爾文表明的那樣:“我跟隨漫長而純粹抽象的思維軌跡的能力極其有限,因此我從來不可能在形而上學或者數學上取得成功。”或者,用約翰·洛克(John Locke)更簡短的話説:“數學證明像鑽石一樣既堅硬又清透。”
數學定理的證明到底是什麼呢?這個問題並不像它看起來那樣一目瞭然,因為它涉及哲學、心理學和數學各方面的因素。亞里士多德對此有深刻的理解,他把證明描述為“不是表面上的陳述而是內心的冥想。”
羅素也做出了令人信服的評論:數學家永遠不可能把“完整的推理過程”寫到紙上,而一定會放置“足以使訓練有素的大腦信服的證明摘要”。他想要説的就是,任何數學陳述都是建立在另一些陳述和定義的基礎之上的,這些陳述和定義又是建立在更多的陳述和定義的基礎之上的,因此要求證明沿着每一個邏輯步驟追蹤回來,也許有點魯莽。然而在 20 世紀初,當羅素與艾爾弗雷德·諾思·懷特海(Alfred North Whitehead,1861-1947)一起合著鉅著《數學原理》時,他似乎忘記了自己給世人的忠告。在這本著作中,他們嘗試着把整個數學回推到基礎的邏輯原理,並在這一過程中保留了細節。其結果是非常折磨人的。他們的展開如此周密,在他們最終證明了 1+1=2 之前,此書已達 362 頁,這一證明在“基數算術導言”一章的 54.43 節(參見圖1)。《數學原理》使論證變得瘋狂。

圖 1 羅素和懷特海證明1+1=2丨摘自艾爾弗雷德·諾思·懷特海和伯特蘭·羅素於 1910 年合寫的《數學原理》的第 1 卷。劍橋大學出版社惠允
在本章,我們要試着保持頭腦清醒。按照我們的意思,證明就是在邏輯法則的範圍內精心製作的推理,對於一個論斷的正確性,它無懈可擊,令人信服。像“説服誰?”或者“按照誰的標準無懈可擊?”等一類問題留作以後再議。
當然,我們也可以選擇考慮什麼不是證明。藉助直觀、常識,或者更糟,藉助暗示的陳述都不是論證。刑事訴訟中作為有罪證明的“排除一切懷疑”的證明,也不是我們所説的論證。數學家認為,證明不僅能排除合理的疑問,而且能夠排除所有疑問。
我們可以從許多不同的方向展開關於數學論證的討論。這裏,我們給出四個重要的基本原則,並逐個闡述涉及數學證明本質的非常有意義的問題。
基本原則#1:個案不充分
無論在科學中,還是在日常生活中,當實驗反覆肯定某個原則之後,我們就傾向於接受它的真實性。如果肯定的案例數量足夠大,我們就説有了一個“被證實的法則”。
但是,對於數學家來説,幾個案例的結果儘管可能給出一些提示,但絕不是證明。下面給出這種現象的一個例子,考慮

這是真的嗎?顯然,我們可以代入幾個正整數看一看有什麼結果。當 n=1 時,我們得到f(1)=1-28+322-1960+6769-13132+13069-5040=1,顯然斷言成立。如果我們代入n=2,計算結果為
f(2)=27-28×26+322×25-1960×24+6769×23-13132×22+13069×2-5040=2
這一次斷言仍然成立。我們希望讀者拿出計算器,驗證一下f(3)=3,f(4)=4,f(5)=5,f(6)=6,甚至f(7)=7。
這個論斷的證據似乎建立起來了。有些人,特別是那些對這樣機械式的計算沒有熱情的人也許已經宣佈這個陳述是真的。但是,它不是真的。代入 n=8 時,我們得到
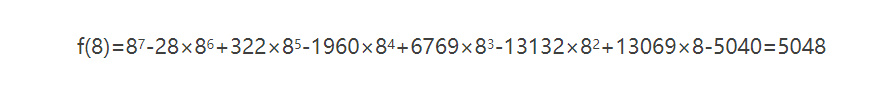
結果不是我們期望的 8。進一步的計算表明f(9)=40329,f(10)=181450,f(11)=640811,所以此斷言不僅失敗了,而且錯得驚人。對於由n=1, 2, 3, 4, 5, 6, 7時都為真得出 n 為任意正整數時都為真的猜測實際上是不正確的。
我們把下面這個表達式展開併合並同類項,就可以得到剛才討論的多項式
f(n)=n+[(n-1)(n-2)(n-3)(n-4)(n-5)(n-6)(n-7)]
顯然,對於n=1,項(n-1)為零,因此方括號中的所有乘積都為零;因此f(1)=1+0=1。如果n=2,那麼n-2=0,所以f(2)=2+0=2。類似地,f(3)=3+0=3,一直到f(7)=7+0=7。但是這之後括號裏的項不再是零,例如f(8)=8+7!=5048。
這引出下面這樣一個富有挑戰性的擴展命題。假設我們引入
g(n)=n+[(n-1)(n-2)(n-3)…(n-1000000)]
並猜測對於所有正整數n,有g(n)=n 。
我們做乘法且合併g(n)的項,就得到一個一百萬次的驚人方程。通過與上面完全相同的推理,我們將發現g(1)=1 ,g(2)=2,一直到g(1000000)=1000000。
在發現了一百萬個連續正確的證據之後,任何思維正常的人都會懷疑g(n)是否總是產生n。對於任何人——除了數學家之外,一百萬次連續成功都等同於排除了所有值得懷疑的證明。然而,再接下來驗證一下,g(1000001)實際上等於1000001+1000000! ,這個數非常大,顯然超過 1 000 001。
上面這個例子強調了關於數學證明的第一個基本原則:我們必須對所有可能的情況進行證明,而不僅是對幾百萬個情況進行證明。
基本原則#2:越簡單越好
數學家讚美那些巧妙的證明。但是,數學家更讚美那些既巧妙又經濟的證明,即那些直擊要害、直達目標的沒有多餘之處的簡潔推理。這樣的證明被認為是優雅的。
數學的優雅與其他創意作品的優雅沒有什麼不同。它與莫奈的油畫藝術的優雅有很多共同之處,僅用寥寥幾筆勾勒或幾行詩描繪的法國鄉村風景,勝過長篇大論。優雅在本質上屬於美學範疇,而不是數學的特性。
同任何理想一樣,優雅不是總能夠實現的。數學家們為簡短、清晰明瞭的證明而奮鬥,但是經常必須忍受令人討厭的煩瑣事物。例如,抽象代數中有限單羣分類的證明用了 5000 多頁紙(最終檢驗通過時)。尋求優雅的人請另尋出路。
相比之下,數學家達到的終極優雅是所謂的“無言的證明”,在這樣的證明中一個極好的令人信服的圖示就傳達了證明,甚至不需要任何解釋。很難比它更優雅了。例如,考慮下面的例子。

但是第一個基本原則警告説,只有傻子才會依據一個案例就匆匆得出結論。我們要利用圖2 去證明這個命題。
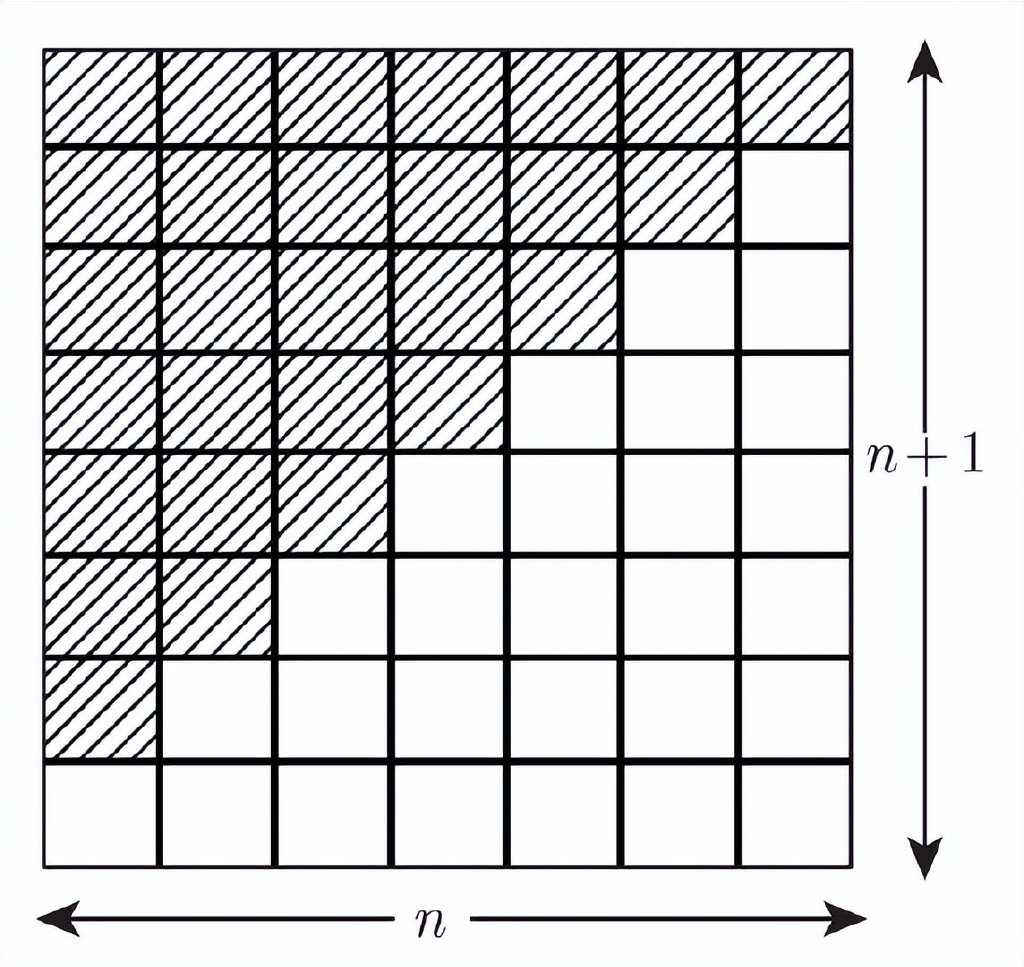
圖2
這裏我們採用由一塊加上兩塊再加上三塊等這樣階梯式的結構,如圖2陰影部分所示;用方塊擺出n×(n+1)的矩形排列。這個矩形是由兩個完全相圖同的階梯組成的,矩形的面積等於它的長和寬的積,即n×(n+1) ,因此這個階梯的面積一定是矩形面積的一半,即
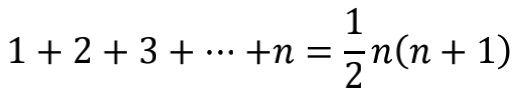
證畢。
讀者也許觀察到這個“無言的證明”仍然伴隨着一段文字解釋。但是,語言的解釋的確沒有必要,這個圖示值千言萬語。(“無言的證明”是美國《大學數學雜誌》的固定專欄。)
下面是另一個不可否認的優雅證明。假設我們從 1 開始把正奇數依次相加:
1+3+5+7+9+11+13+…
一些經驗提示我們,無論把這個加法進行到什麼時候,其結果總是完全平方數。例如,
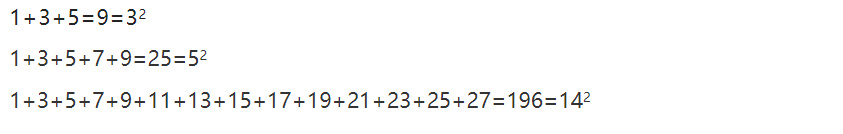
這永遠為真嗎?如果是,我們如何證明這個一般結果?
下面的推理需要一點代數知識,根據觀察:偶數是 2 的倍數,因此對某個整數n,其形式是2n ;而奇數比 2 的倍數少 1,因此對某個整數n,其形式是2n-1。
定理 從 1 開始的連續奇數之和是一個完全平方。
證明 設 S 是從 1 開始到2n-1(n>0)的連續奇數之和,即
S=1+3+5+7+…+(2n-1)
顯然我們可以求從 1 到 2n 為止的所有整數的和,然後再減去偶數之和就可以得到連續奇數之和。換句話説
S=[1+2+3+4+5+…+(2n-1)+2n]-(2+4+6+8+…+2n)
=[1+2+3+4+5+…+(2n-1)+2n]-2(1+2+3+4+…+n)
這裏,我們從第二個方括號的表達式中提出了一個因子 2。
第一個方括號中是從 1 到 2n 的所有整數的和,而第二個方括號中是從 1 到 n 的所有整數的和。圖2的“無言的證明”展示瞭如何求這樣的整數和,所以我們兩次利用那個結果:
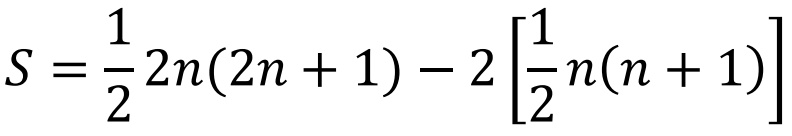
化簡上式得到
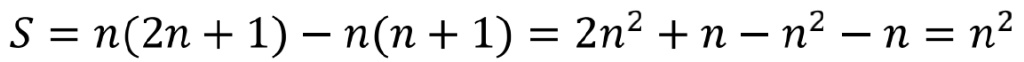

一句話,這個證明是優雅的。但是,如果它是我們尋找的那種優雅,那麼圖3則給出了另一個更短的證明,一個無言的證明。這裏奇數是一個方塊、三個方塊、五個方塊,以此類推,按特殊方法排列。我們從左下角的一個方塊開始,三個有陰影的方塊包圍着它形成一個2×2 的正方形,五個沒陰影的方塊包圍着前面這些方塊形成一個 3×3 的正方形,接下來就是七個有陰影的方塊包圍着前面這些方塊形成一個 4×4 的正方形,以此類推。這張圖示清楚地表明從 1 開始的連續奇數的和總是產生一個(幾何的)平方。這個證明非常自然。早在 2000 年前古希臘人就知道它了,現代的後輩可以通過構建方塊模仿這一證明。
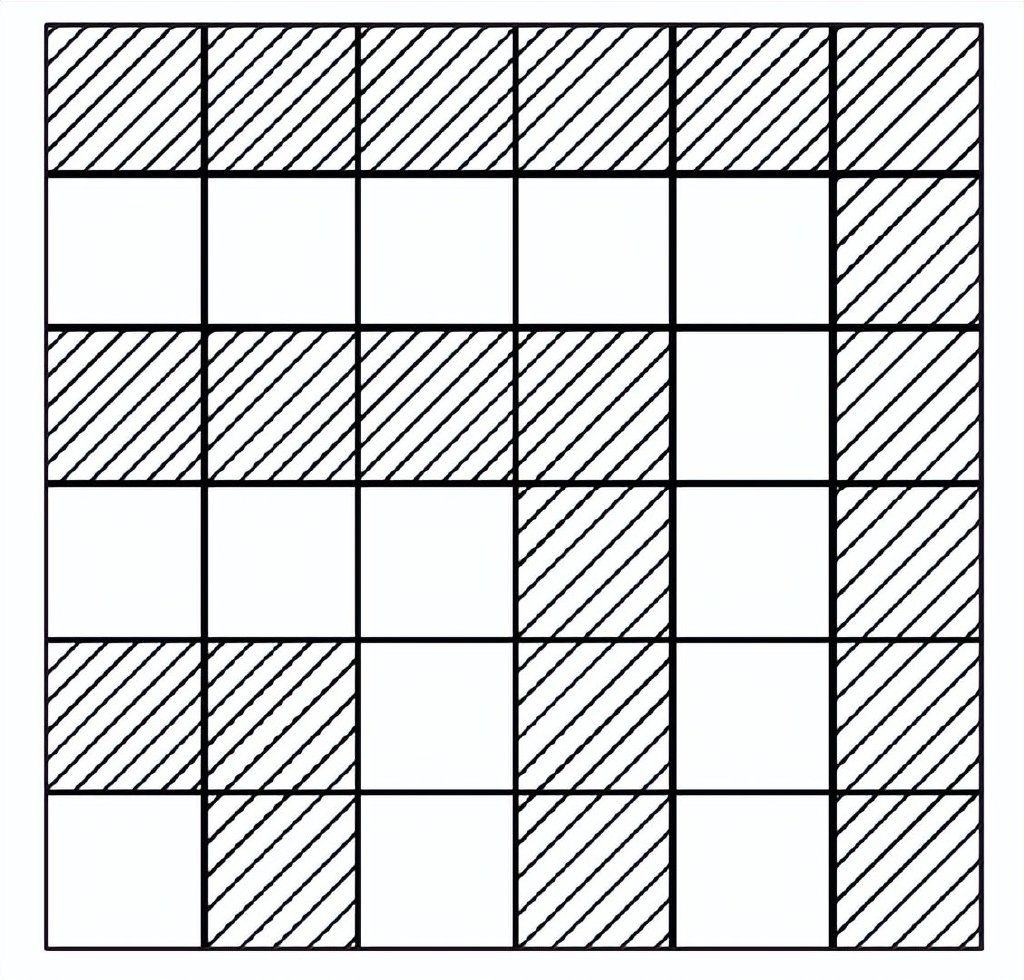
圖3
温斯頓·丘吉爾(Winston Churchill)説:“短小的詞為佳,而既古老又短小的詞為最佳。”我們可以重新描述這個優雅推理:古老的證明為佳,而既古老又短小的證明為最佳。
基本原則#3:反例的價值
數學中有一個非常嚴酷的現實:為了證明一個一般的陳述需要一個一般的推理;但為了反駁它,只需要一個特殊的例子,一個使這個陳述失敗的例子。後者稱為反例,一個好的反例價值如金。例如,假設我們有下面的猜測。

我們強調,儘管可能需要 50 頁紙的推理來證明一個定理,但是隻要一行反例就可以反駁它。在證明和反證之間的大戰中,似乎沒有一個公平的競爭環境。但是,還是要説一句警告的話:尋找反例不像看起來那樣容易。下面的故事就是一個例子。
兩個多世紀前,歐拉猜測至少要把三個完全立方加起來才能得到另一個完全立方,至少要把四個完全四次冪相加才能得到另一個完全四次冪,至少要把五個完全五次冪相加才能得到另一個完全五次冪,等等。

讀過第 F 章的讀者應該意識到,這是費馬最後定理的特殊情況 (n=3)。
提高次數,我們能夠找到四個完全四次冪,它們之和等於一個四次冪。例如,考慮下面絕非一目瞭然的例子:
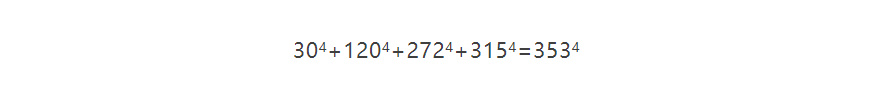
歐拉猜測三個四次冪之和不會產生另一個四次冪,但是沒有給出證明。一般地,他説至少需要n個n次冪,使得它們之和等於另一個n次冪。
這件事在 1778 年成立,近兩個世紀後它仍然成立。信任歐拉的人不能用證明來肯定歐拉的猜測,但不相信歐拉的人也不能構造出一個特殊的反例來駁倒它。這個問題是一個未解問題。
到了 1966 年,數學家利昂·蘭德(Leon Lander)和托馬斯·帕金(Thomas Parkin)發現了下面這個例子:

這表明三個四次冪,而不是歐拉説的四個四次冪,也能生成一個四次冪。
尋找這些反例需要大量努力,甚至動用了計算機的力量,這是非常驚人的。這顯然給出了基本原則 #3 的一個推論:有時候反證比證明更難。
基本原則#4:可以證明否定
在理髮店或快餐店裏,我們經常聽到這樣一句老話:你不能證明否定。它可能是由下面這樣的對話引發的:
A:“超市小報説一個小妖精中了獎。”
B:“沒有小妖精這種東西。”
A:“你説什麼呢?”
B:“我説小妖精不存在。”
A:“你肯定嗎?你能夠證明它不存在嗎?”
B:“當然……不能。但是你也不能證明它存在。”
這個對話很長。用一句話説,它聲稱我們絕對不能證明小妖精不存在。
數學家知道得更清楚。一些最偉大、最重要的數學推理所論證的就是某些數、某些形狀、某些幾何結構不存在且不可能存在。人們使用最猛烈的武器,即理性的、嚴密的邏輯確立了這些不存在的事物。
認為否定不可證明的這種普遍觀念本質上是錯誤的。為了證明小妖精不存在,我們似乎需要翻遍愛爾蘭島上的每一塊石頭,翻遍南極洲的每一座冰山。當然這是不可能實現的野心。
為了在邏輯上確立不存在的事物,數學家採用了一種非常不同然而又非常完美的策略:假設這個對象的確存在,然後再追蹤由此產生的結果。如果我們能夠證明存在的假設將導致一個矛盾的話,那麼邏輯法則允許我們得出結論:我們在第一步中所做的存在的假設是錯誤的。因此,我們就能夠得出這個事物不存在的毫無爭議的結論,同時也説明一個事實,即我們採用了一個非直接的途徑所得到的這個結果是正確的。
在第 Q 章中,我們將討論最著名的不存在證明:為什麼不存在等於
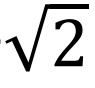
的分數?然而,對於我們眼前的目標,下面這個例子就足夠了。
定理 不存在邊長分別為 2, 3, 4, 10 的四邊形。
處理這個問題的一個實用方法是截出這些長度的木棍,然後試着把它們擺放成一個有四條邊的圖形。這只是一個説明,然而在邏輯的意義下,這相當於要在某塊岩石下找到一個小妖精。即使我們花費了好多年都沒有成功地用這四根木棍擺出一個四邊形,也不能排除也許某個人在某天成功地把它們擺成四邊形的可能性。
合理的方法是我們要間接地證明一個否定。開始我們假設存在一個四邊形,它的邊長分別是 2, 3, 4, 10,然後再設法生成一個矛盾,這是一個戰略上的飛躍。
我們假設的四邊形如圖4 所示。畫出虛線所示的對角線,它把這個四邊形分成兩個三角形,並設 是這條對角線的長度。第 G 章(古希臘幾何)已經説明過,歐幾里得證明了三角形的任意一條邊小於其他兩條邊的和。因此在△ABC 中,我們知道10<4+x。同樣在△ADC 中,有x<2+3。把這兩個不等式結合起來得到
10<4+x<4+(2+3)=9
根據上面的不等式,得到10<9。這是不可能的。我們最初所做的存在這種特殊的四邊形的假設導出了這一矛盾,所以説我們的假設是無效的。
這個四邊形的四條邊長的出現順序(按順時針)是 10, 2, 3, 4。還有其他方法放置這四條邊,如圖5所示,同樣的推理也導出一個矛盾。此時是10<2+x<2+(3+4)=9 。這是不可能的。
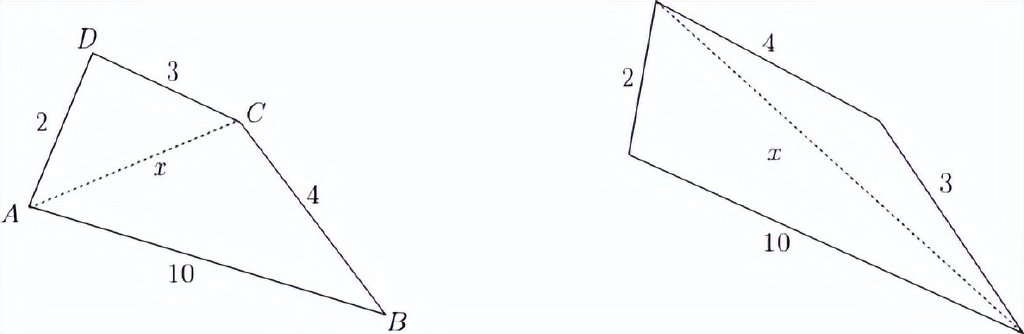
圖4和圖5
沒有必要再繼續尋找了,重新佈局再多次也是沒有意義的。這樣的四邊形是不可能存在的。我們最終證明了一個否定。
基於矛盾的證明是一個非常好的邏輯策略。假設我們想要證明的反面是成立的,我們似乎是在毀滅自己的目標。但是,最後我們避開了災難。哈代把基於矛盾的證明描述為“數學家最好的武器之一。它遠比其他任何先手棋策略好得多:象棋手也許要犧牲一個小卒或者其他一枚棋子,但是數學家犧牲的卻是整盤遊戲“。
問題:還需要人類嗎?
大約在 20 世紀 70 年代到 80 年代期間,有一種令人不安的映像闖入數學家的意識之中。這就是計算機映像,它以光一樣的速度和實質上的可靠性接手了證明定理的工作。

令整個數學界感到困惑的是此後出現的一些利用計算機來證明定理的情況。這些情況往往把一個定理分解成很多子情況,假如肯定了每一種子情況,那麼就可以斷定解決了整個問題。遺憾的是,這種分析通常需要考慮上百種情況,需要成千上萬次計算,而人類沒有可能重複所有步驟。總之,這樣的證明只能通過其他機器來檢查。
1976 年,計算機證明憑藉解決四色猜想問題戲劇般地登上了數學舞台。所謂的四色猜想,是任何畫在平面的地圖都可以用四種(或少於四種)顏色着色,使得擁有共同邊界的任意兩個區域都被塗上不同的顏色。(例如在圖6中,我們不想給區域 A 和 B 都塗上紅色,因為那樣一來它們的公共邊界線會被遮住。我們允許給相交於一點的兩個區域,如區域 A 和 C 塗上相同的顏色,當然一個點不是邊界線。)
四色猜想誕生於 1852 年,在接下來的一個世紀裏引起了廣泛的關注。有幾個問題很快就被解決了,比如任何平面地圖肯定可以用五種顏色着色,還有就是用三種顏色着色地圖是不充分的。圖 7就給出了這樣的一個地圖。在這張圖上,我們必須使區域 A、B 和 C 有不同的顏色,因為它們每對都有共同的邊界,但是接下來,除非使用第四種顏色,否則不可能給區域 D 着色。
因此,五種顏色(可能)太多而三種顏色又不夠。顯然這就需要四種顏色。四種顏色足以給任何平面地圖着色嗎?
我們之前的討論表明,要想解決這個問題只有兩種選擇:要麼提出一個特殊的反例,即給出一種不能用四種顏色着色的特殊地圖;要麼設計一個一般的證明,證明任何地圖都能夠這樣着色。對於數學家來説,這個反例很難找到。他們製作的每一張地圖無論多麼錯綜複雜,都能僅用紅色、黃色、藍色和綠色着色。(有蠟筆的讀者也許想立即勾畫出一張地圖,然後嘗試一下。)
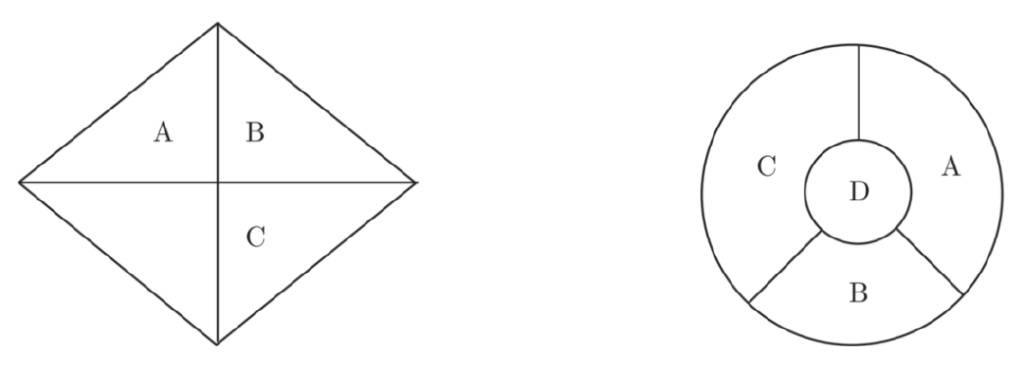
圖6和圖7
但是,正如我們反覆提醒的那樣,證明可不光是找到幾個反例就算完成了。以前人們會發瘋地尋找一般推理,但事實證明每一種情況都與尋找反例一樣困難。局勢處於停頓的狀態。
後來,美國伊利諾伊大學的阿佩爾(Kenneth Appel)與哈肯(Wolfgang Haken)宣佈四色猜想為真,震撼了整個數學界。令人們感到震驚的不是這個結論,而是他們的證明技術:計算機完成了證明中最艱難的部分。
阿佩爾和哈肯處理這個問題的方法是,把所有平面地圖分成某些類型,然後分別分析每一種類型。遺憾的是,一共有上百種類型需要檢查,每一種類型都給高速計算機帶來大量的工作。最後,計算機宣告這個猜測是真的,即所有可能的類型都可以用四種顏色着色。這個定理得到了證明。
這是真的嗎?説句公道話,當時一種不安的情緒在整個數學界蔓延。這算得上是一個正確的論證嗎?令人困惑的是,回答這個問題需要一個真正的有血有肉的人每週工作 60 小時,花費大約 100 000 年的時間去檢查計算機的計算。甚至是最健康、最樂觀的人也不可能活那麼長時間,總之,誰願意花這個工夫呢?
如果程序出現了錯誤怎麼辦?如果功率突增使得計算機跳過關鍵的步驟怎麼辦?如果計算機的硬件設計暴露出極少見的微小缺陷怎麼辦?總之,我們能夠相信機器大腦能給我們真理嗎?正如數學家羅恩· 格雷厄姆(Ron Graham)在考慮這些複雜問題時提出的那樣:“實質的問題是這樣的:如果沒有人能夠檢查一個證明,它還是一個真正的證明嗎?”
直到今天,這個問題也沒有明確的答案,儘管隨着計算機證明變得更加普遍,也許數學家們對它們的出現會感到稍舒服些,但是,公正地説,如果四色定理擁有寫了兩頁紙那樣短小、睿智而優雅的證明,而不是依靠計算機的蠻力得到的證明,那麼大多數數學家也許會輕鬆地喘口氣。傳統主義者希望古老的數學不要被接上電源。
“還需要人類嗎?”此時這個問題的答案仍然是“需要”。畢竟得有人打開空調吧。但是我們得承認這個觀點也許是有偏見的,因為它的支持者本身是人。
我們關於數學論證的討論到此就結束了。顯然,還有很多話要説,也應該引出其他的議題,應該提出其他的基本原則。但是,我們最終得出的最重要的結論是:無論是優雅還是麻煩,是直接還是間接,是依賴於計算機還是人力,數學證明的標準不同於其他任何人類活動領域中的標準。
前往“返樸”公眾號,點擊下圖或左下角“閲讀原文“購買↓↓

特 別 提 示
1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閲不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回覆四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。
版權説明:歡迎個人轉發,任何形式的媒體或機構未經授權,不得轉載和摘編。轉載授權請在「返樸」微信公眾號內聯繫後台。